Optimal controlled variable selection for individual process units

Optimal controlled variable selection for individual process units Ramprasad Yelchuru Sigurd Skogestad Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 1

Outline 1. Problem formulation, c = Hy 2. Convex formulation (full H) 3. CVs for Individual unit control (Structured H) 4. MIQP formulations 5. Distillation Case study 6. Conclusions CV – Controlled Variables MIQP - Mixed Integer Quadratic Programming Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 2

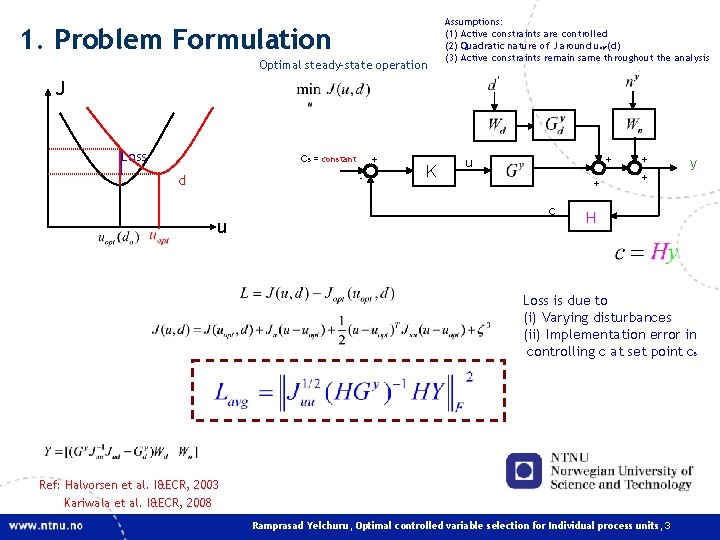
1. Problem Formulation Optimal steady-state operation Assumptions: (1) Active constraints are controlled (2) Quadratic nature of J around uopt(d) (3) Active constraints remain same throughout the analysis J Loss cs = constant d + - u K u + + c + y + H Loss is due to (i) Varying disturbances (ii) Implementation error in controlling c at set point cs Ref: Halvorsen et al. I&ECR, 2003 Kariwala et al. I&ECR, 2008 Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 3

2. Convex formulation (full H) Seemingly Non-convex optimization problem D : any non-singular matrix Objective function unaffected by D. So can choose freely. We made H unique by adding a constraint as subject to Problem is convex in decision matrix H Full H Convex optimization problem Global solution Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 4

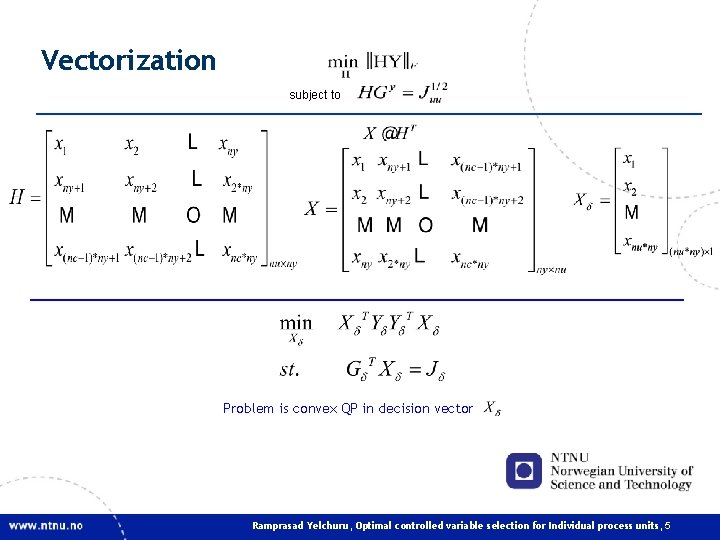
Vectorization subject to Problem is convex QP in decision vector Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 5

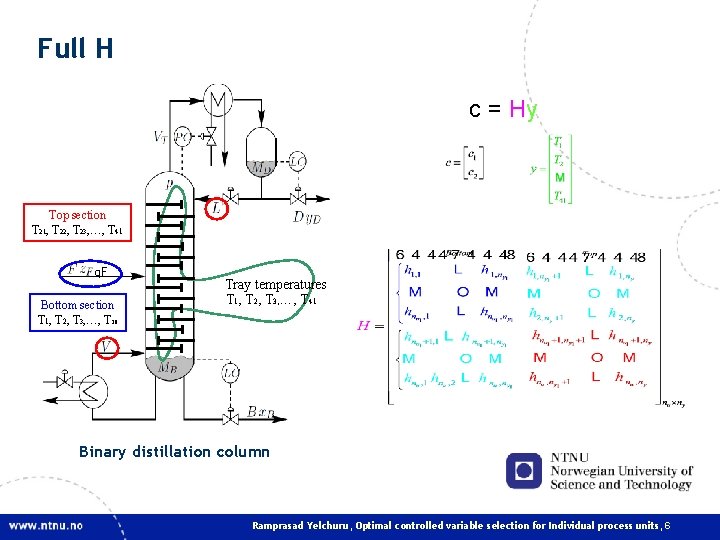
Full H c = Hy Top section T 21, T 22, T 23, …, T 41 q. F Bottom section T 1, T 2, T 3, …, T 20 Tray temperatures T 1, T 2, T 3, …, T 41 Binary distillation column Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 6

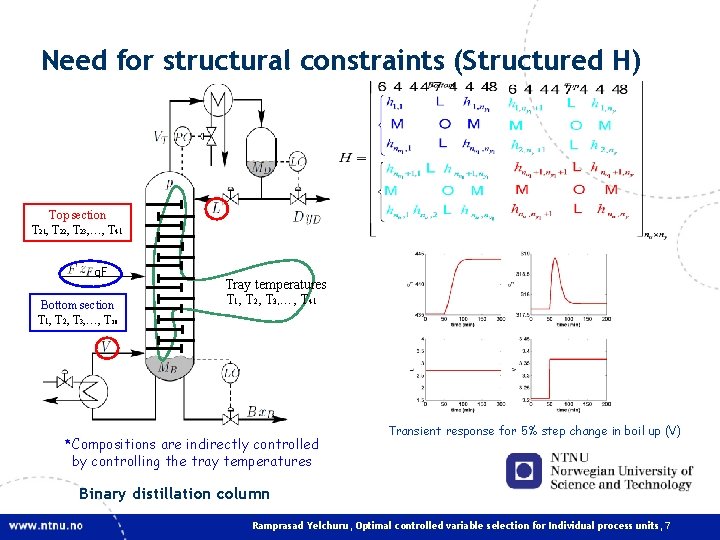
Need for structural constraints (Structured H) Top section T 21, T 22, T 23, …, T 41 q. F Bottom section T 1, T 2, T 3, …, T 20 Tray temperatures T 1, T 2, T 3, …, T 41 *Compositions are indirectly controlled by controlling the tray temperatures Transient response for 5% step change in boil up (V) Binary distillation column Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 7

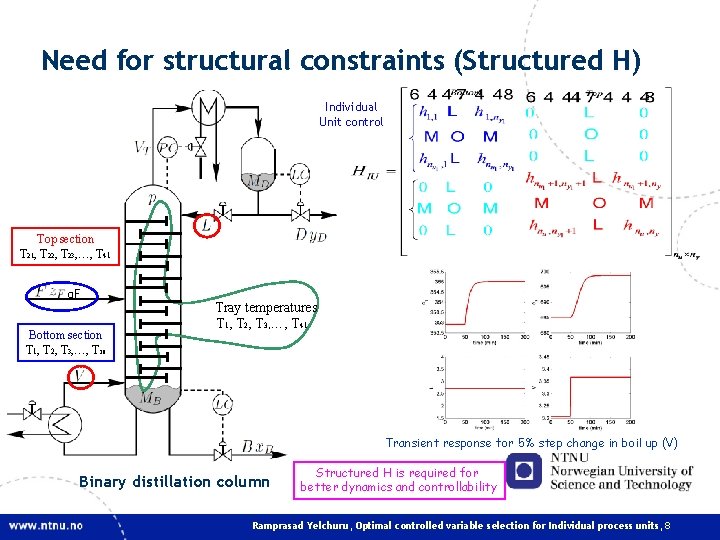
Need for structural constraints (Structured H) Individual Unit control Top section T 21, T 22, T 23, …, T 41 q. F Bottom section T 1, T 2, T 3, …, T 20 Tray temperatures T 1, T 2, T 3, …, T 41 Transient response for 5% step change in boil up (V) Binary distillation column Structured H is required for better dynamics and controllability Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 8

3. CVs for Individual Unit control (Structured H) D : any non-singular matrix For individual unit control HIU only block diagonal D preserve the structure in H and So we can use D to match certain elements of to Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 9

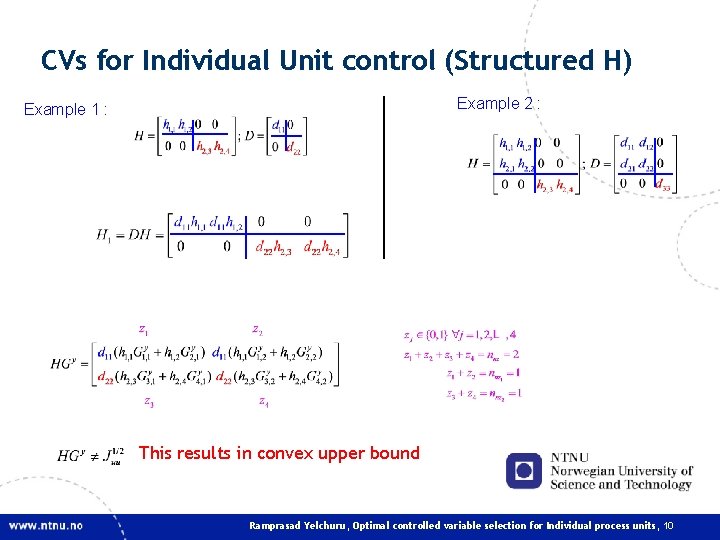
CVs for Individual Unit control (Structured H) Example 2 : Example 1 : This results in convex upper bound Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 10

Controlled variable selection Individual unit control Optimization problem : st. Minimize the average loss by selecting H and CVs as (i) best individual measurements (ii) best combinations of all measurements (iii) best combinations with few measurements Minimize the average loss by selecting H and CVs as (i) best individual measurements of disjoint measurement sets (ii) best combinations of disjoint measurement sets of all measurements (iii) best combinations of disjoint measurement sets with few measurements Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 11

4. MIQP Formulation (full H) Big M approach We solve this MIQP for n = nu to ny Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 12

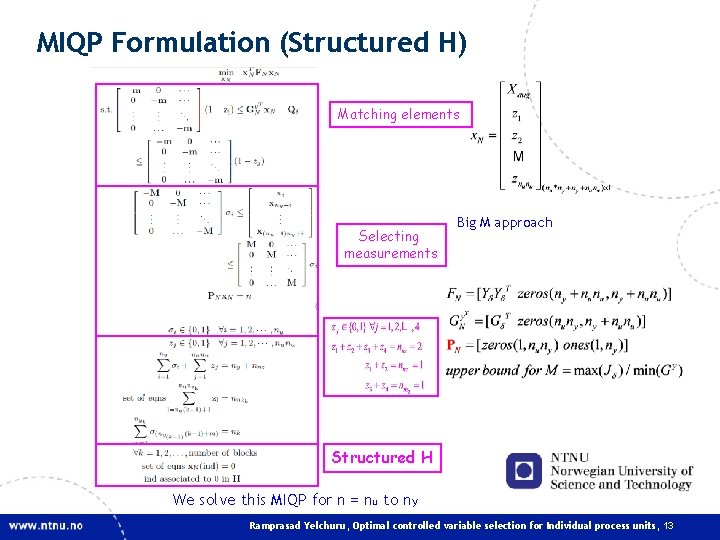
MIQP Formulation (Structured H) Matching elements Selecting measurements Big M approach Structured H We solve this MIQP for n = nu to ny Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 13

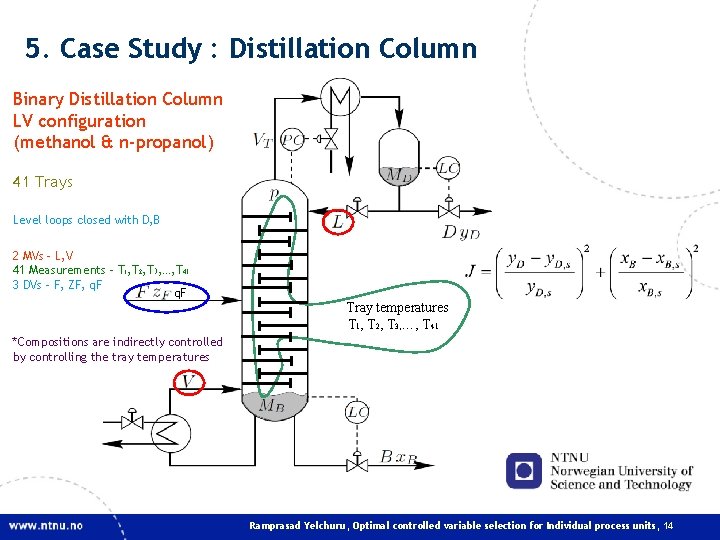
5. Case Study : Distillation Column Binary Distillation Column LV configuration (methanol & n-propanol) 41 Trays Level loops closed with D, B 2 MVs – L, V 41 Measurements – T 1, T 2, T 3, …, T 41 3 DVs – F, ZF, q. F Tray temperatures T 1, T 2, T 3, …, T 41 *Compositions are indirectly controlled by controlling the tray temperatures Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 14

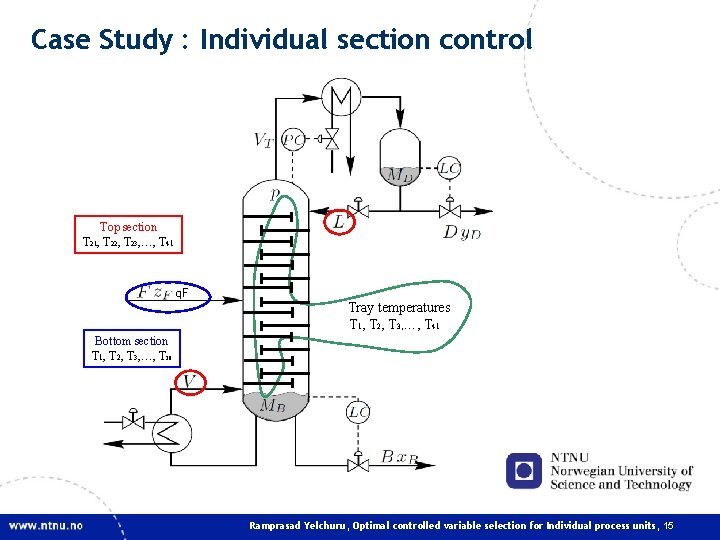
Case Study : Individual section control Top section T 21, T 22, T 23, …, T 41 q. F Tray temperatures T 1, T 2, T 3, …, T 41 Bottom section T 1, T 2, T 3, …, T 20 Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 15

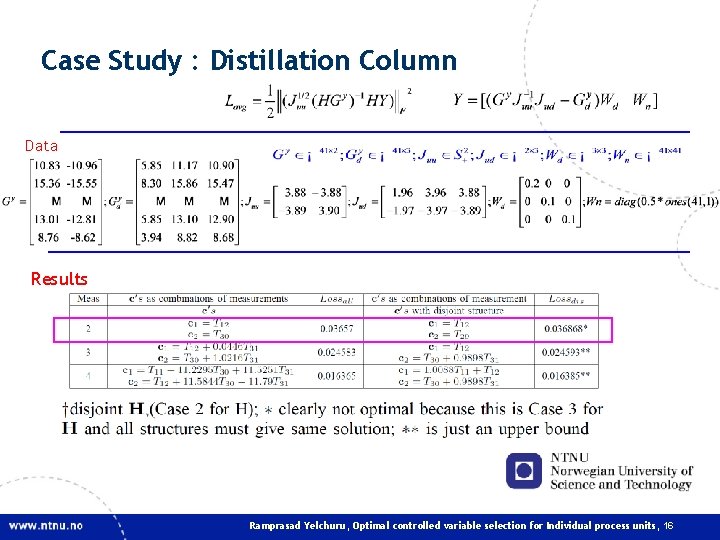
Case Study : Distillation Column Data Results Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 16

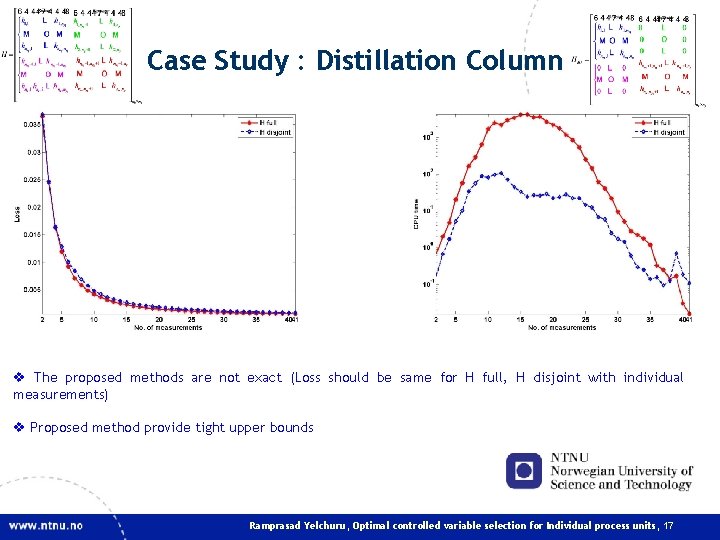
Case Study : Distillation Column v The proposed methods are not exact (Loss should be same for H full, H disjoint with individual measurements) v Proposed method provide tight upper bounds Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 17

6. Conclusions Using steady state economics of the total plant, the optimal controlled variables selection as v optimal individual measurements from disjoint/(individual unit) measurement sets v combinations of optimal fewer measurements from disjoint/(individual unit) measurement sets is solved using MIQP based formulations. The proposed methods are not exact, but provide upper bounds to Loss to find CVs as combinations of measurements from individual units. Ramprasad Yelchuru, Optimal controlled variable selection for Individual process units, 18