Optimal Capital Structure The Cost of Capital Approach

Optimal Capital Structure The Cost of Capital Approach P. V. Viswanath Based on Damodaran’s Corporate Finance

Cost of Capital Approach w We have already seen that n FCFF = EBIT(1 -t) – (Capital Expenditures – Dep) – Change in Noncash Working Capital w The Value of the firm is the sum of the discounted present values of FCFF plus current cash. w If we can assume that the cashflows are unaffected by the choice of financing mix, then n Max Firm Value = Min WACC P. V. Viswanath 2

Cost of Equity Capital w We compute WACC at different debt/capital ratios and pick the lowest WACC. w Three inputs needed: n n n Cost of equity After-tax cost of debt Weights on debt and equity w Start with the current equity beta and compute the firm’s asset beta. w Compute the firm’s levered beta for different debt ratio levels and use this to figure out the cost of equity capital at the different debt ratio levels. P. V. Viswanath 3

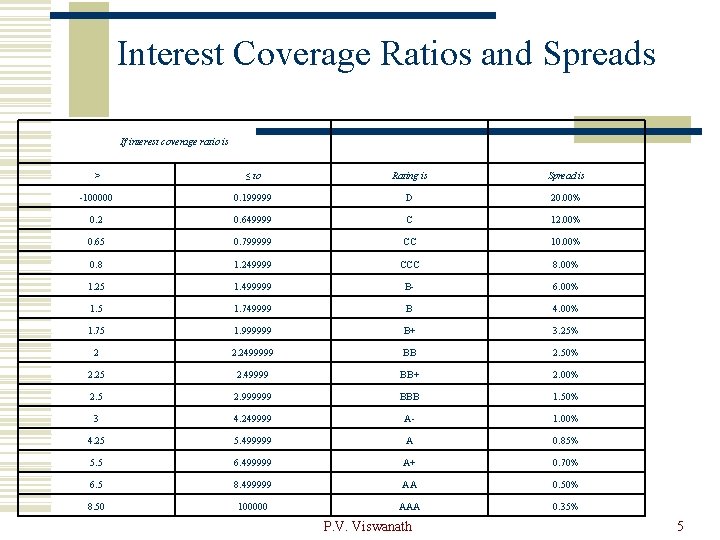
Cost of debt capital w Estimate the firm’s dollar debt and interest exp at each debt ratio. w At each debt ratio, n n compute a financial ratio(s) such as the interest coverage ratio (EBIT/Interest expenses) to measure default risk; use that ratio(s) to estimate a synthetic bond rating for the firm. Add on a default spread based on the estimated rating to the risk-free rate to get the pre-tax cost of debt. Apply the marginal tax rate to get the after-tax cost of debt, keeping in mind that the marginal tax rate might decrease as we increase the amount of debt-related income deductions for tax purposes. w Weight the costs of debt and equity based on the proportions used of each type. w Choose the debt ratio that minimizes the WACC. P. V. Viswanath 4

Interest Coverage Ratios and Spreads If interest coverage ratio is > ≤ to Rating is Spread is -100000 0. 199999 D 20. 00% 0. 2 0. 649999 C 12. 00% 0. 65 0. 799999 CC 10. 00% 0. 8 1. 249999 CCC 8. 00% 1. 25 1. 499999 B- 6. 00% 1. 5 1. 749999 B 4. 00% 1. 75 1. 999999 B+ 3. 25% 2 2. 2499999 BB 2. 50% 2. 25 2. 49999 BB+ 2. 00% 2. 5 2. 999999 BBB 1. 50% 3 4. 249999 A- 1. 00% 4. 25 5. 499999 A 0. 85% 5. 5 6. 499999 A+ 0. 70% 6. 5 8. 499999 AA 0. 50% 8. 50 100000 AAA 0. 35% P. V. Viswanath 5

Constrained Approach w The unconstrained approach is problematic because agency costs are going to increase as the debt ratio goes up and as the bond rating goes down. w To keep a limit on these costs, the firm might want to put a constraint on the lowest bond rating allowed. w Use normalized operating income to estimate bond ratings so that temporarily depressed income does not yield an overly low optimal debt ratio. w Lower estimates of operating income for higher debt ratios due to indirect bankruptcy costs. P. V. Viswanath 6

Example w Problem 12, Chapter 19 from Damodaran, Corporate Finance, Theory and Practice w You have been asked by JJ Corporation, a California-based firm that manufactures and services digital satellite television systems, to evaluate its capital structure. They currently have 70 million shares outstanding trading at $10 per share. In addition, it has 500, 000 ten-year convertible bonds, with a coupon rate of 8%, trading at $1000 per bond. JJ Corporation is rated BBB, and the interest rate on BBB straight bonds is currently 10%. The beta for the company is 1. 2, and the current risk-free rate is 6%. The tax rate is 40%. P. V. Viswanath 7

Debt-Equity Ratio computation w a. What is the firm's current debt-equity ratio? w Solution: The market value of the common stock is 70 m. x $10 = $700 m. The 500, 000 convertible bonds would sell at a yield of 10% if they were straight. Hence the straight bond component of the convertibles = w Since the convertibles trade at $1000 per bond, the equity component = $124. 63 per convertible bond. Hence total equity = 700+124. 63(0. 5 m. ) = 762. 32 m. The market value of the debt component of the convertibles = 875. 37(0. 5) = 437. 69 m. Hence the debt-equity ratio = 437. 69/762. 32 = 57. 41%. P. V. Viswanath 8

WACC Computation w b. What is the firm's current weighted average cost of capital? w Solution: The required rate of return on the equity, using the CAPM is. 06 + 1. 2(0. 055) = 12. 6%. w The WACC = (. 5741/1. 5741)(1 -0. 4)10% + (1/1. 5741)12. 6% = 10. 192%, using the data from the previous section. P. V. Viswanath 9

Cost of equity after borrowing w JJ Corporation is proposing to borrow $250 million to use for the following purposes: n n Buy back $100 million Pay $100 million in dividends Invest $50 million in a project with a NPV of $25 million. The effect of this additional borrowing will be a drop in the bond rating to B, which currently carries an interest rate of 11%. w c. What will be the firm's cost of equity after this additional borrowing? P. V. Viswanath 10

Cost of equity after borrowing w Solution: After this borrowing, the market value of equity will be $762. 32 m - $200 m + $25 m. = $586. 5 m. The market value of debt will be 437. 69+250=687. 69 m. w Hence the debt-equity ratio will be 1. 17. The unlevered beta = Hence the levered beta will be equal to 0. 89(1+(1 -0. 4)1. 17) = 1. 52. w Hence, the cost of equity =. 06+1. 52(0. 055) = 14. 36%. P. V. Viswanath 11

WACC after borrowing w d. What will the firm's weighted average cost of capital be after this additional borrowing? w Solution: The WACC = P. V. Viswanath 12

Value of firm after borrowing w e. What will the value of the firm be after this additional borrowing? w Solution: The original firm value was $1200. The WACC has decreased from 10. 192% to 10. 17%; hence the annual savings in financing costs equal (1200)(. 10192 -. 1017). w Discounting these at the new cost of capital of 10. 17%, we get (762. 32+437. 68)(. 10192 -. 1017)/(0. 1017) = $2. 36 m. w New Firm Value= $ 1, 200 (original firm value) + $ 50 (net increase in capital after capital structure changes)+ $ 25 (NPV of new project) + $ 2. 36 (increase in firm value due to capital structure change) = $ 1277. 36 million. P. V. Viswanath 13