Optics Reflection and Refraction Reflection When a wave



























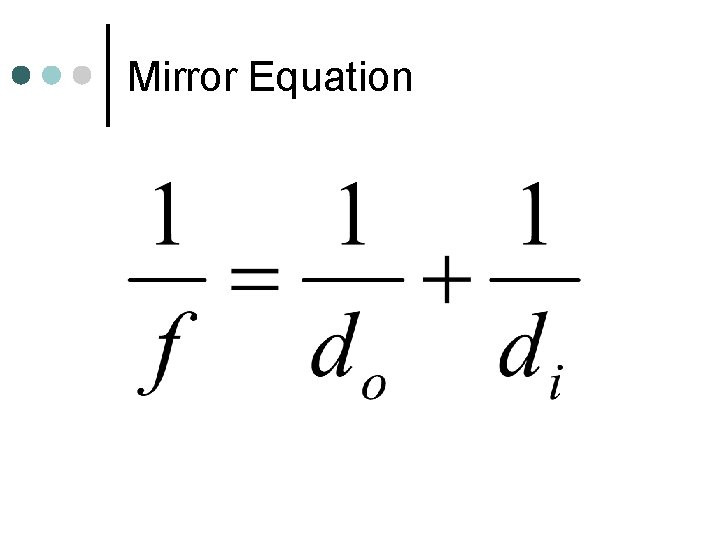




- Slides: 58

Optics Reflection and Refraction

Reflection ¢ When a wave encounters a new medium or barrier some of the wave is bounced back (reflected), and some is transmitted (refracted)

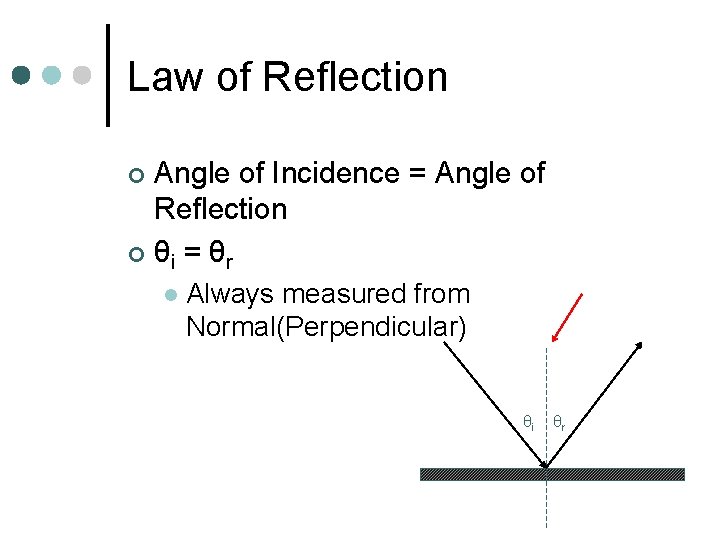
Law of Reflection Angle of Incidence = Angle of Reflection ¢ θi = θr ¢ l Always measured from Normal(Perpendicular) θi θr

Image Types Real – Light rays actually travel to that location ¢ Virtual – Light appears to be at that location ¢ Upright – image is right side up compared to object ¢ Inverted – image is upside down as compared to object ¢

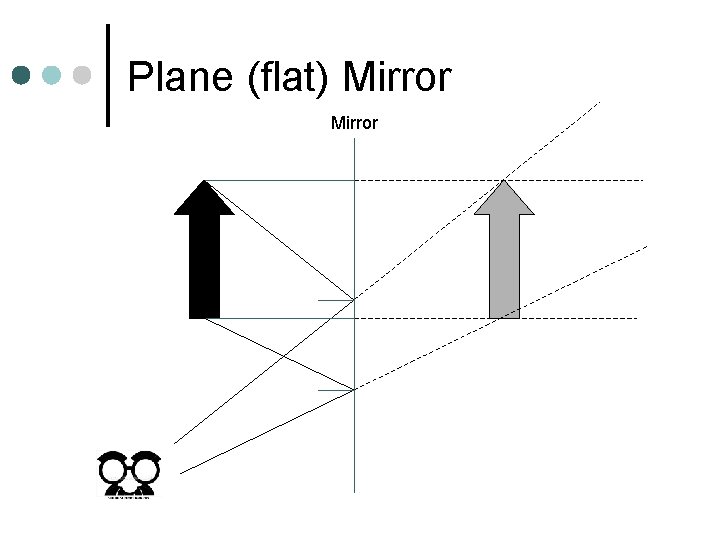
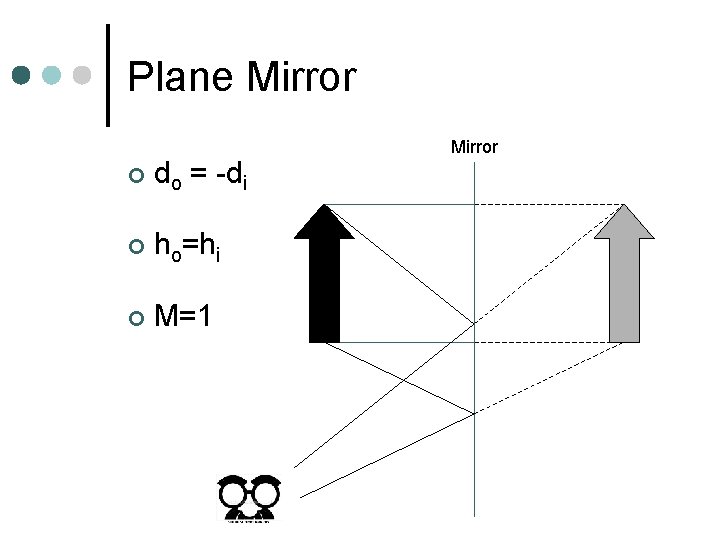
Plane Mirror ¢ Flat, smooth surface from which light is reflected. ¢ The distance the object is away from the mirror is equal to the distance the image appears to be “in” the mirror

Plane (flat) Mirror

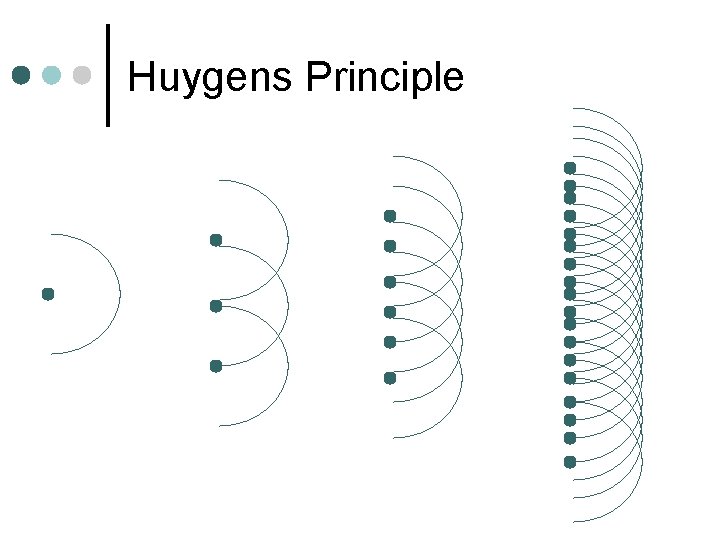
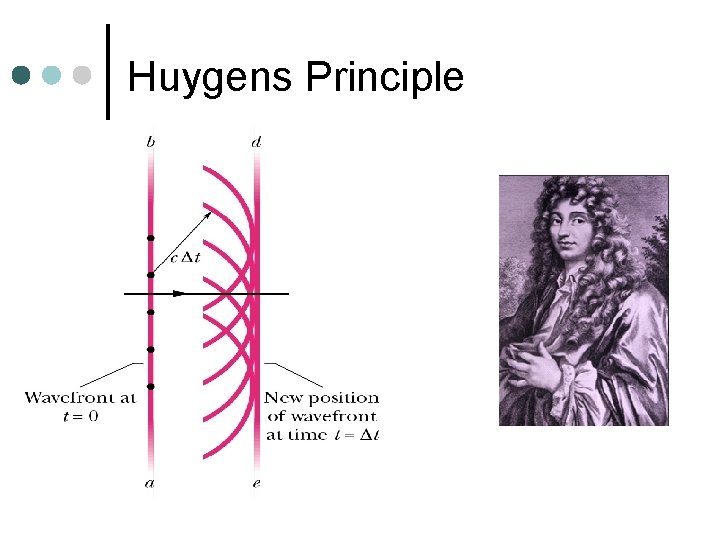
Huygens Principle ¢ Every point on a propagating wave front serves as a source of a spherical secondary wavelet ¢ The corresponding spherical wavelets produce further wave fronts ¢ Basis for Diffraction, Reflection, Refraction

Huygens Principle

Huygens Principle

Huygens Principle ¢ First proposed explanation that light is a wave ¢ Newton later proposed that light is a particle

Question ¢ Compared to running down the road, if you were to run in thick mud…. ¢ Would you go as fast? Speed decreases ¢ Would your steps be as long? Wavelength decrease

Refraction ¢ Changing of speed when wave enters new material (frequency remains constant) ¢ Speed decreases in more dense material l ¢ Wavelength decreases Speed increases in less dense material l Wavelength increases

Refraction Example Air ¢ ¢ Water Freqair=Freqwater because the color remains the same Since the wavelength changes, the velocity must change proportionately

Index of Refraction (n) ¢ Measure of the optical density of a material l Table in the Reference Tables

Refraction ¢ When a wave enters a new medium, it changes speed. When a wave enters a new medium, it changes direction ¢ Simulation ¢

Refraction

Refraction

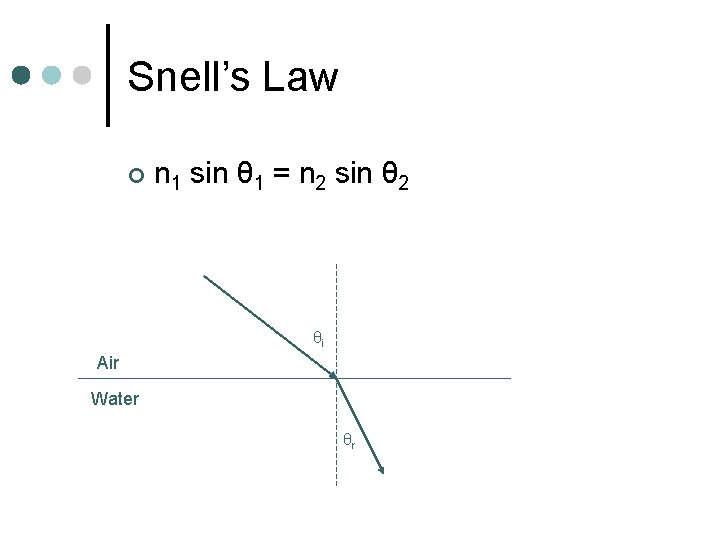
Snell’s Law ¢ n 1 sin θ 1 = n 2 sin θ 2 θi Air Water θr

Snell’s Law ¢ When a wave enters a more dense material, the wave will bend TOWARDS the normal ¢ When a wave enters a less dense material, the wave will bend AWAY from the normal

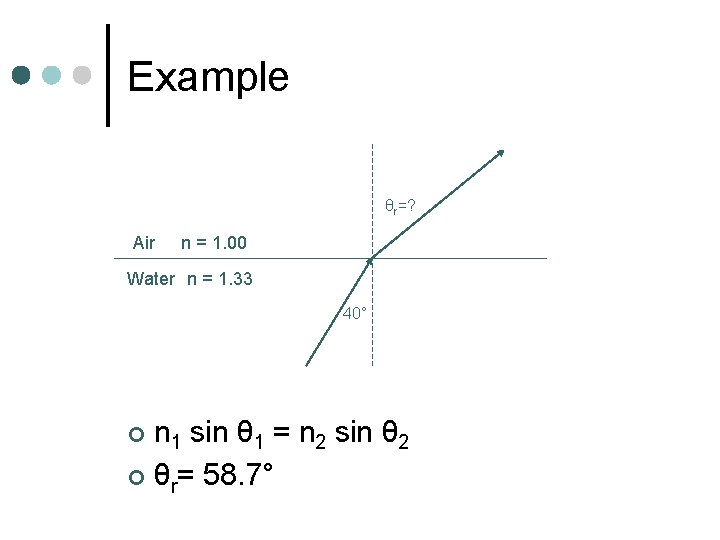
Example θr=? Air n = 1. 00 Water n = 1. 33 40° n 1 sin θ 1 = n 2 sin θ 2 ¢ θr= 58. 7° ¢

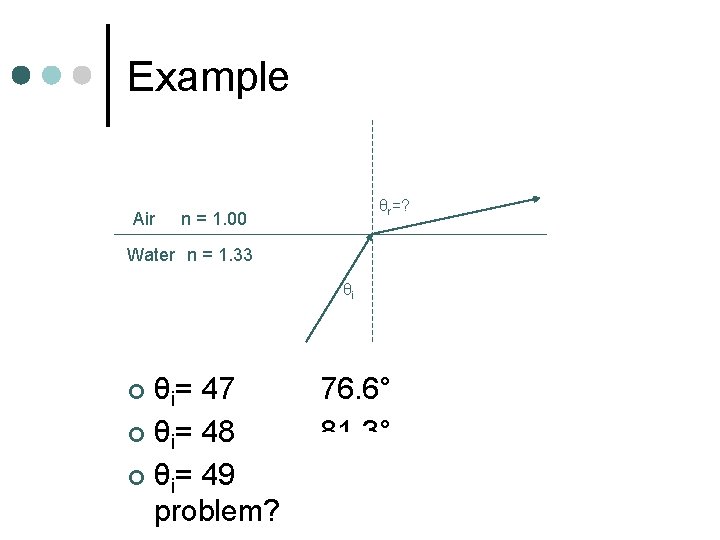
Example Air θr=? n = 1. 00 Water n = 1. 33 θi θi= 47° θr= 76. 6° ¢ θi= 48° θr= 81. 3° ¢ θi= 49° θr= ? problem? ¢ Is there a

Total Internal Reflection ¢ At a certain incident angle the refracted ray will be at 90°. l ¢ Critical Angle, θc At angles greater than the Critical Angle, the ray is reflected back into the material. Air n = 1. 00 Water n = 1. 33 θi θr

Total Internal Reflection ¢ n 1 sin θC = n 2 sin θ 2 = 1 ¢ n 1 sin θC = n 2 ¢ n 1 > n 2

Dispersion ¢ Spreading of light into its color components ¢ Index of refraction is based on frequency of light ¢ Index varies for different frequencies

Dispersion

Curved Mirrors and Lenses

Vocabulary ¢ Object distance, do l ¢ Distance object is from optical device Image distance, di l Distance image is from optical device

Vocabulary ¢ Object Height, ho l ¢ Height of object Image Height, hi l Height of image

Vocabulary ¢ Real Image formed by actual intersection of light rays l Image can be projected on a screen l di=(+) l

Vocabulary ¢ Virtual Image (imaginary) Light rays do not intersect l Image can NOT be projected on screen l The eye traces back the rays to where they appeared to have once intersected l di=(-) l

Vocabulary ¢ Upright Image Object Image is of the same orientation as object l hi = (+) l ¢ Inverted Image is inverted from the orientation of the object l hi = (-) l Object Image

Vocabulary ¢ Magnification, M Ratio of the image height to the object height l M=(+) image is upright l M=(-) image is inverted l

Plane Mirror ¢ do = -di ¢ ho=hi ¢ M=1 Mirror

Spherical Mirrors ¢ Concave Mirrors l ¢ Mirror surface is on the inside of the curve Convex Mirrors l Mirror surface is on the outside of the curve

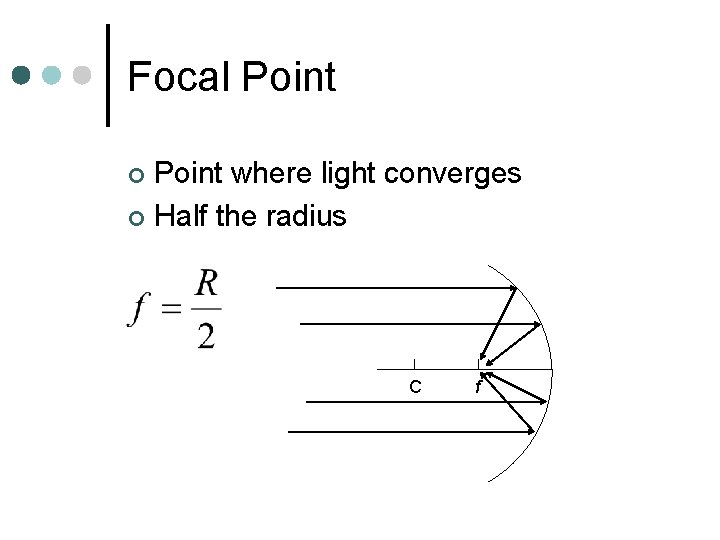
Focal Point where light converges ¢ Half the radius ¢ C f

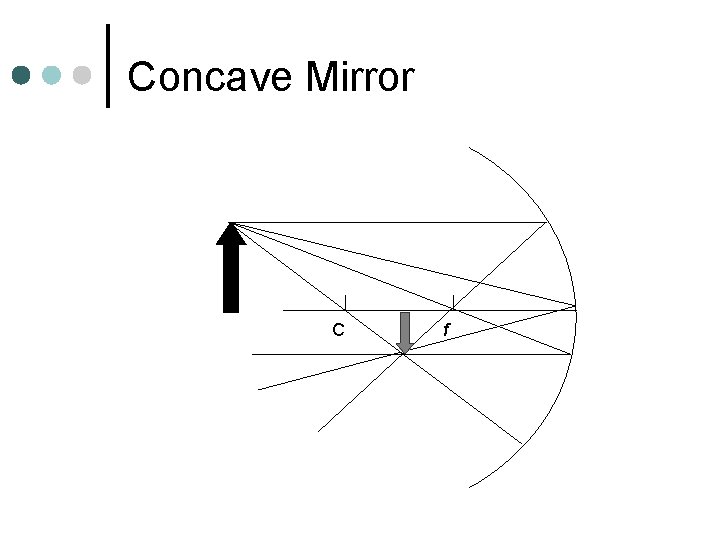
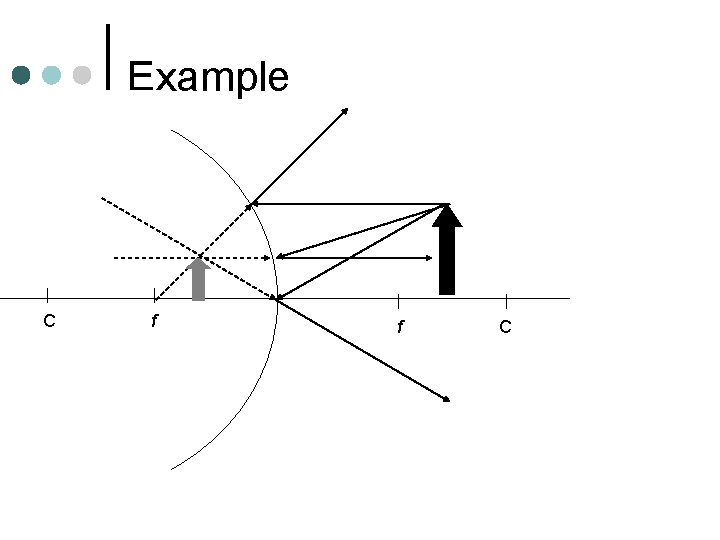
Concave Mirror ¢ Ray that is initially parallel to central axis reflects through focal point ¢ Ray that is initially through focal point reflects parallel to central axis ¢ Ray that is incident at vertex, reflects at same angle ¢ Ray that travels through center of curvature will reflect back through center of curvature

Concave Mirror C f
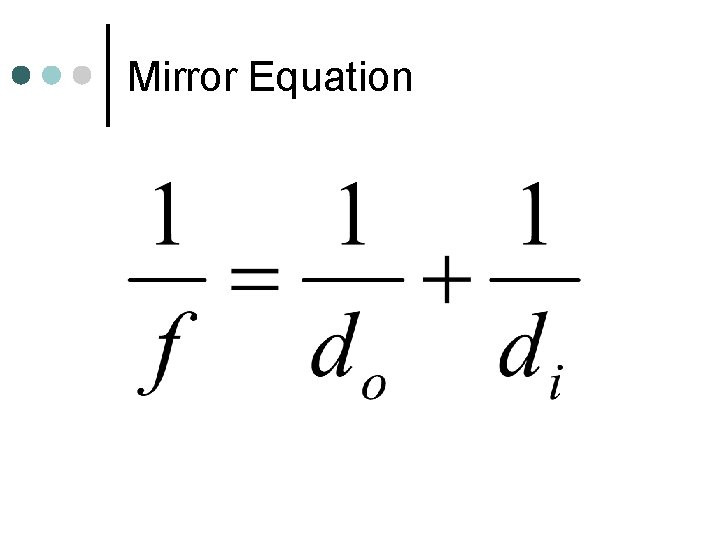
Mirror Equation

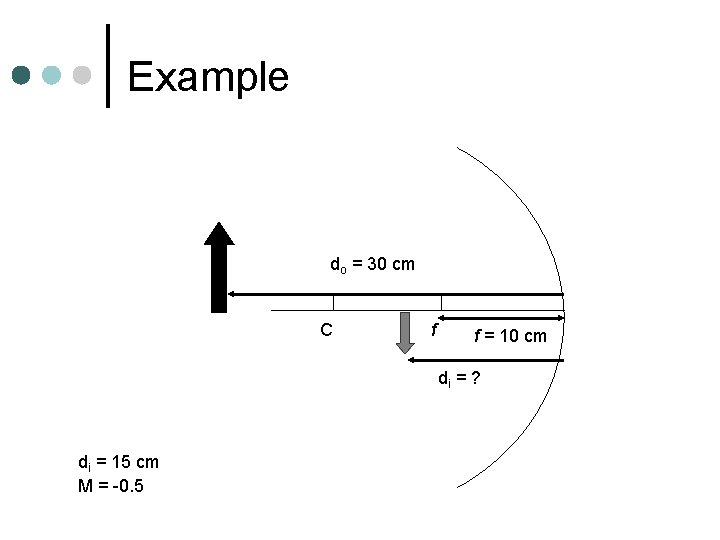
Example do = 30 cm C f f = 10 cm di = ? di = 15 cm M = -0. 5

Convex Mirror ¢ Ray that is initially parallel to central axis reflects through virtual focal point ¢ Ray that is initially through virtual focal point reflects parallel to central axis ¢ Ray that is incident at vertex, reflects at same angle ¢ Ray that travels through center of curvature will reflect back through center of curvature

Example C f f C

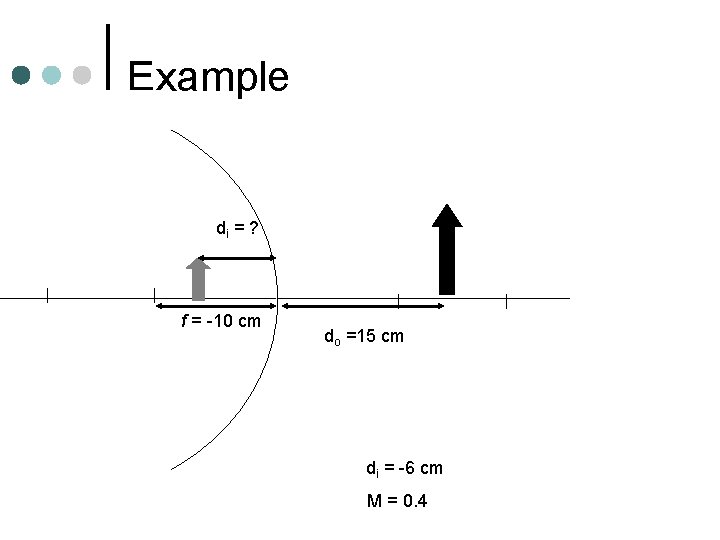
Example di = ? f = -10 cm do =15 cm di = -6 cm M = 0. 4

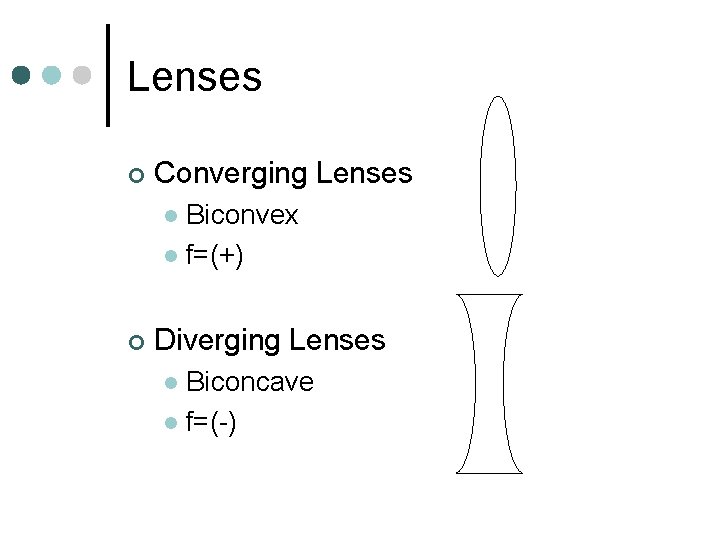
Lenses ¢ Converging Lenses Biconvex l f=(+) l ¢ Diverging Lenses Biconcave l f=(-) l

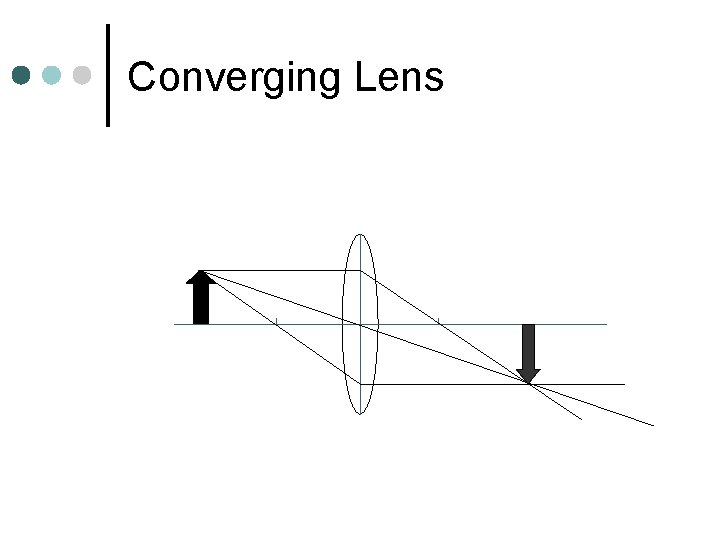
Converging Lens Rays ¢ Ray that is initially parallel to central axis will refract through far focal point ¢ Ray that is initially through near focal point will refract parallel to central axis ¢ Ray that passes through center of lens pass without refraction

Converging Lens

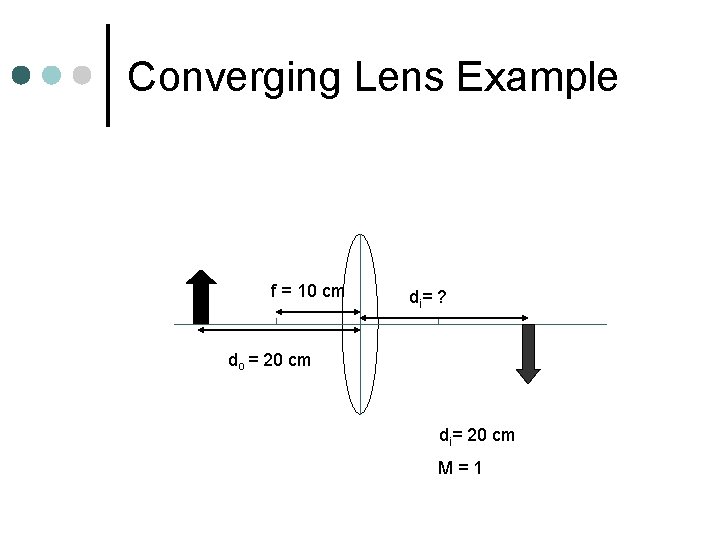
Converging Lens Example f = 10 cm di= ? do = 20 cm di= 20 cm M=1

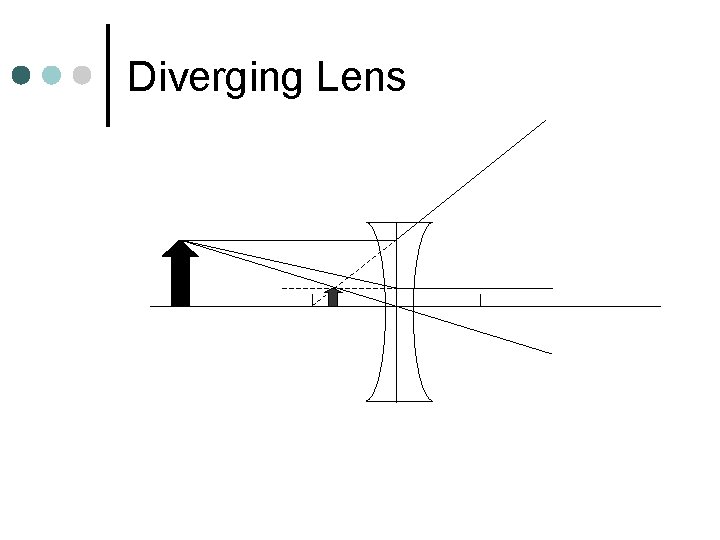
Diverging Lens Rays ¢ Ray that is initially parallel will refract as if coming from near focal point ¢ Ray that is initially through far focal point will refract as if coming from parallel ¢ Ray that passes through center will continue on

Diverging Lens

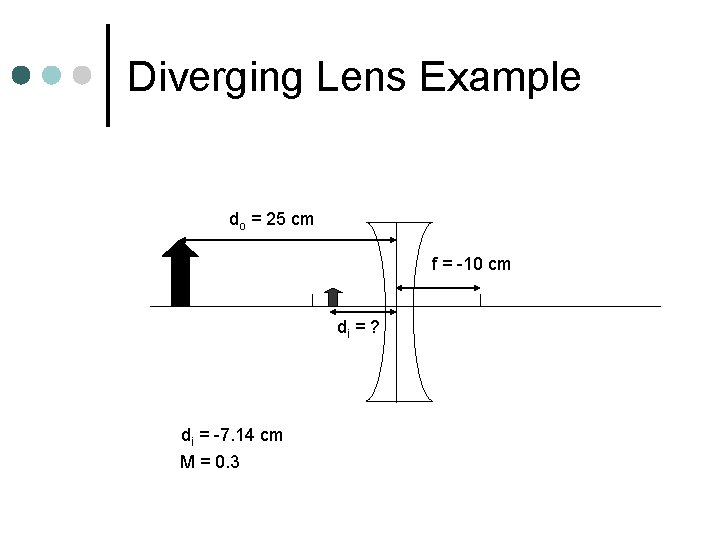
Diverging Lens Example do = 25 cm f = -10 cm di = ? di = -7. 14 cm M = 0. 3

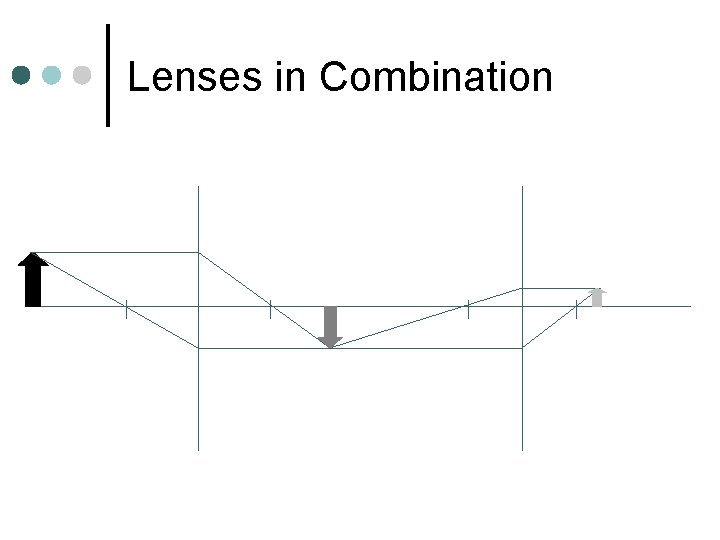
Lenses in Combination ¢ Image from the first lens becomes the object for the second lens

Lenses in Combination

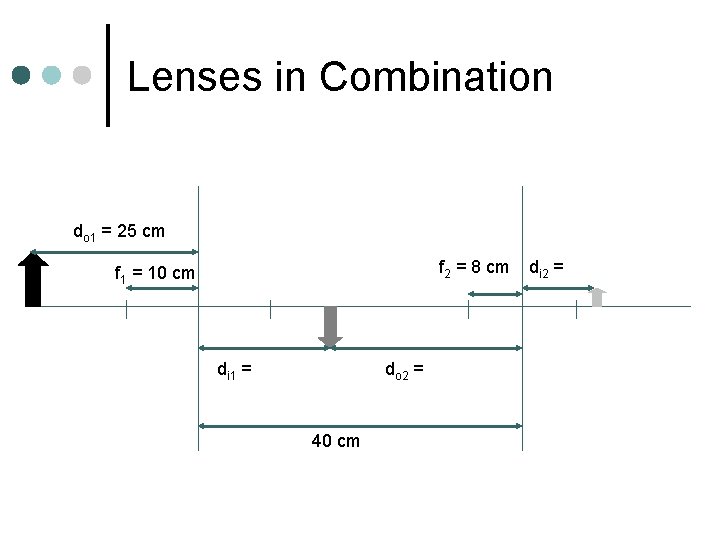
Lenses in Combination do 1 = 25 cm f 2 = 8 cm f 1 = 10 cm di 1 = 16. 7 cm 40 cm do 2 = 23. 3 cm di 2 = 12 cm