Opticalphase conjugation in differencefrequency generation A Andreoni M

Optical-phase conjugation in difference-frequency generation A. Andreoni, M. Bondani, F. Paleari Dept. Sciences, Univ. Insubria and Istituto Nazionale di Fisica della Materia, I. N. F. M. Como, Italy V. N. Mikhailov Photophysics of Holographic Processes Department, S. I. Vavilov State Optical Institute St. Petersburg, Russia

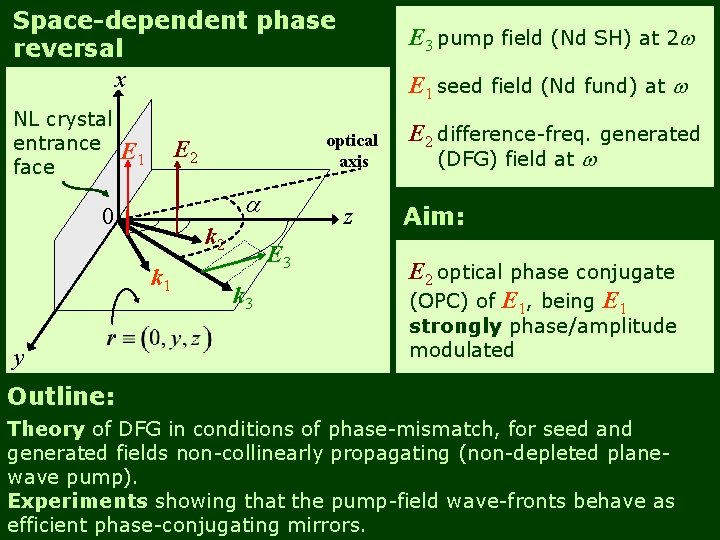
Space-dependent phase reversal x E 3 pump field (Nd SH) at 2 w NL crystal entrance face E 2 difference-freq. generated a 0 k 2 k 1 y optical axis E 2 E 1 seed field (Nd fund) at w z E 3 k 3 (DFG) field at w Aim: E 2 optical phase conjugate (OPC) of E 1, being E 1 strongly phase/amplitude modulated Outline: Theory of DFG in conditions of phase-mismatch, for seed and generated fields non-collinearly propagating (non-depleted planewave pump). Experiments showing that the pump-field wave-fronts behave as efficient phase-conjugating mirrors.

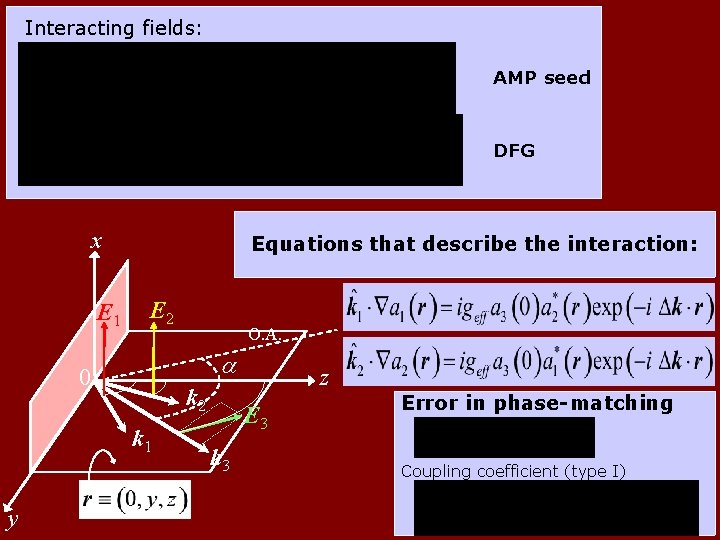
Interacting fields: AMP seed DFG x E 1 Equations that describe the interaction: E 2 a 0 k 2 k 1 y O. A. z E 3 k 3 Error in phase-matching Coupling coefficient (type I)

Property of the equations: conservation law Solutions Boundary conditions

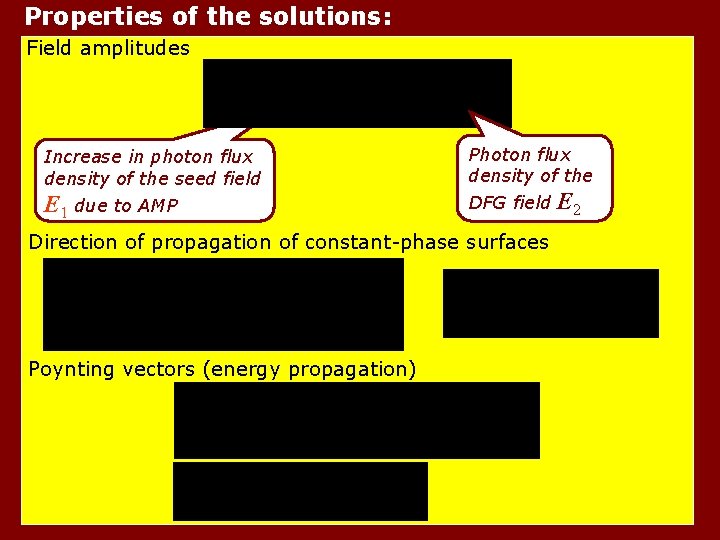
Properties of the solutions: Field amplitudes Increase in photon flux density of the seed field E 1 due to AMP Photon flux density of the DFG field E 2 Direction of propagation of constant-phase surfaces Poynting vectors (energy propagation)

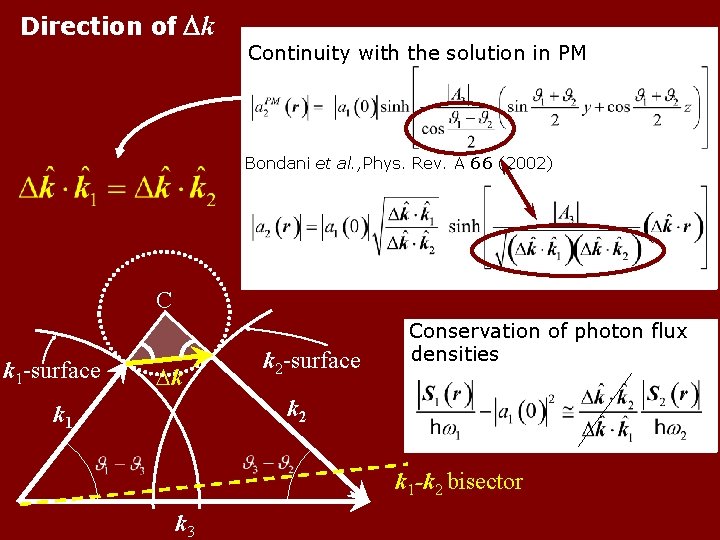
Direction of Dk Continuity with the solution in PM Bondani et al. , Phys. Rev. A 66 (2002) C k 1 -surface Dk k 2 -surface Conservation of photon flux densities k 2 k 1 -k 2 bisector k 3

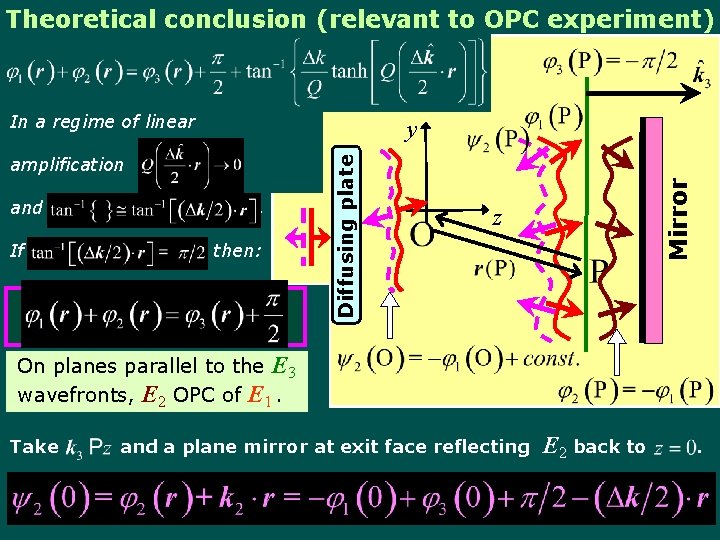
Theoretical conclusion (relevant to OPC experiment) In a regime of linear and If . then: Mirror amplification Diffusing plate y z On planes parallel to the E 3 wavefronts, E 2 OPC of E 1. Take and a plane mirror at exit face reflecting E 2 back to .

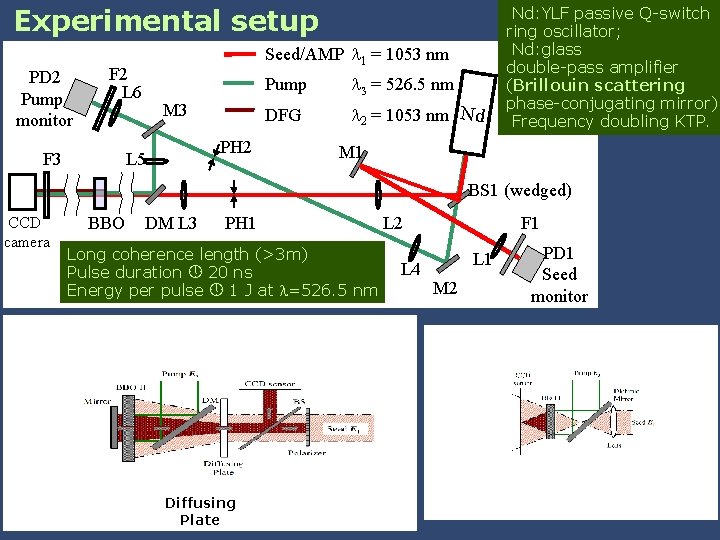
Experimental setup PD 2 Pump monitor Seed/AMP 1 = 1053 nm F 2 L 6 F 3 M 3 PH 2 L 5 Pump 3 = 526. 5 nm DFG 2 = 1053 nm Nd Nd: YLF passive Q-switch ring oscillator; Nd: glass double-pass amplifier Nd: YLF (Brillouin scattering phase-conjugating mirror) source Frequency doubling KTP. M 1 BS 1 (wedged) CCD camera BBO DM L 3 PH 1 Long coherence length (>3 m) Pulse duration 20 ns Energy per pulse 1 J at =526. 5 nm Diffusing Plate L 2 L 4 F 1 L 1 M 2 PD 1 Seed monitor

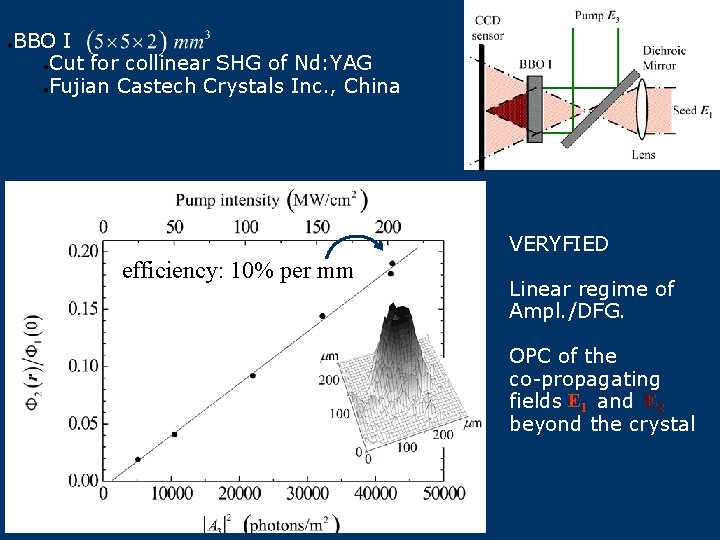
● BBO I ●Cut for collinear SHG of Nd: YAG ●Fujian Castech Crystals Inc. , China VERYFIED efficiency: 10% per mm Linear regime of Ampl. /DFG. OPC of the co-propagating fields E 1 and E 2 beyond the crystal

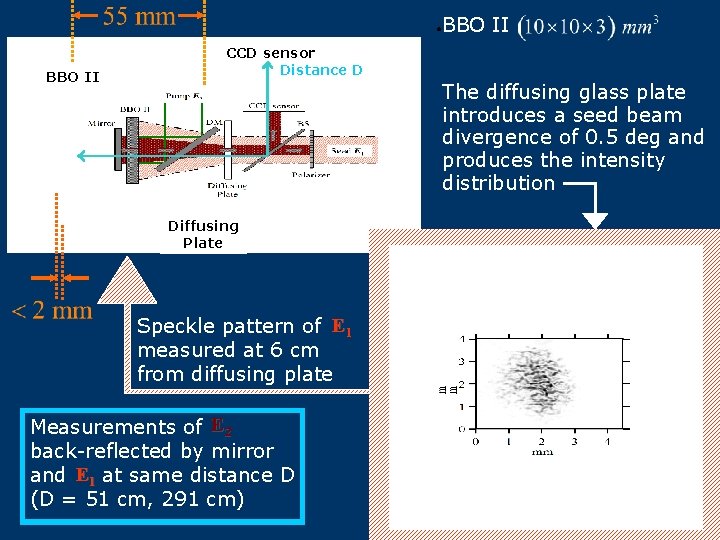
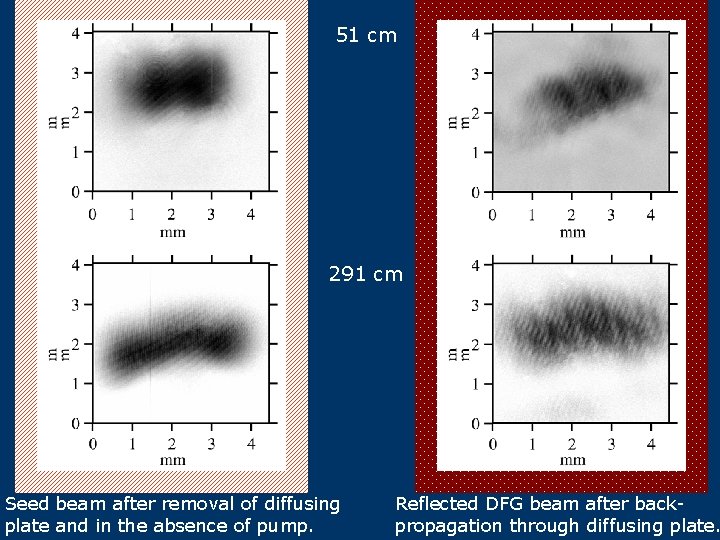
● BBO II CCD sensor Distance D The diffusing glass plate introduces a seed beam divergence of 0. 5 deg and produces the intensity distribution Diffusing Plate Speckle pattern of E 1 measured at 6 cm from diffusing plate Measurements of E 2 back-reflected by mirror and E 1 at same distance D (D = 51 cm, 291 cm)

51 cm 291 cm Seed beam after removal of diffusing plate and in the absence of pump. Reflected DFG beam after backpropagation through diffusing plate.

THANKS TO CO-AUTHORS AND TO AUDIENCE Paper in press: J. Opt. Soc. Am. B (Aug. 2003) Viktor N. Mikhailov Maria Bondani Fabio Paleari