Optical Mineralogy Use of the petrographic microscope John

Optical Mineralogy Use of the petrographic microscope © John Winter, Whitman College with some slides © Jane Selverstone, University of New Mexico, 2003

Why use the microscope? ? • • Identify minerals (no guessing!) Determine rock type Determine crystallization sequence Document deformation history Observe frozen-in reactions Constrain P-T history Note weathering/alteration © Jane Selverstone, University of New Mexico, 2003

The petrographic microscope Also called a polarizing microscope In order to use the scope, we need to understand a little about the physics of light, light and then learn some tools and tricks… tricks © Jane Selverstone, University of New Mexico, 2003

What is light? • A wave or a particle (photon)? • Wave theory: light travels wavelike from point A to point B with electrical and magnetic properties (electromagnetic radiation)

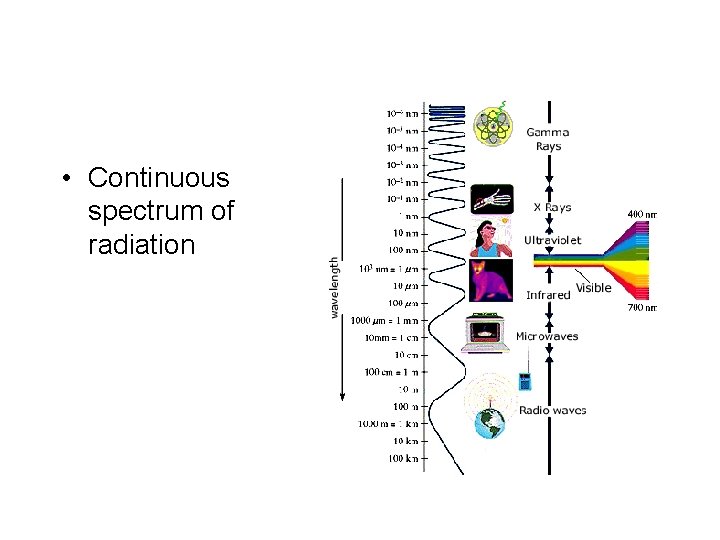
• Continuous spectrum of radiation

Electromagnetic spectrum & visible portion Violet (400 nm) Red (700 nm) White = ROYGBV (can be separated by dispersion in a prism)

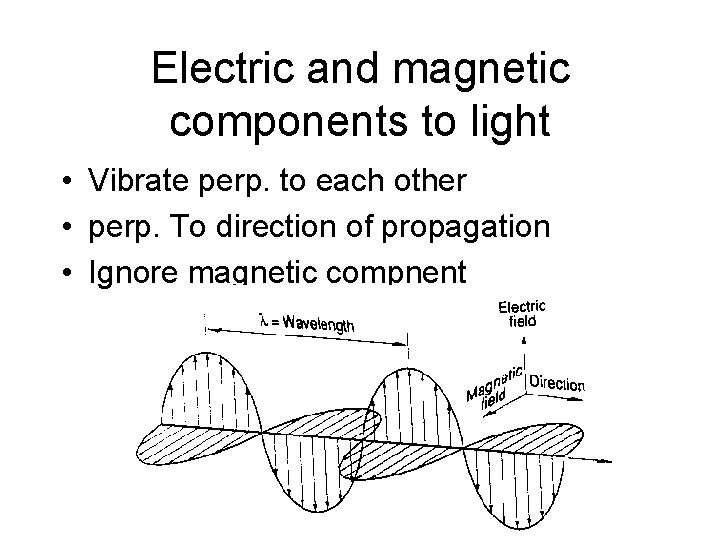
Electric and magnetic components to light • Vibrate perp. to each other • perp. To direction of propagation • Ignore magnetic compnent

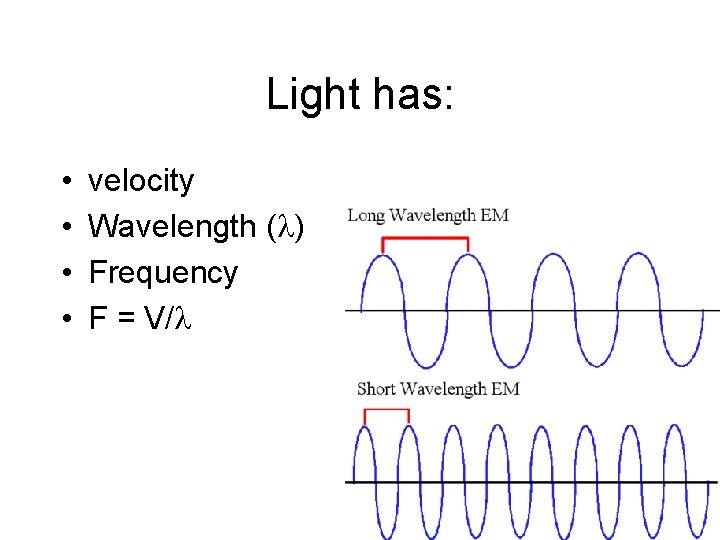
Light has: • velocity • Wavelength ( )

Light has: • • velocity Wavelength ( ) Frequency F = V/

• Frequency is constant • Change wavelength, must change velocity

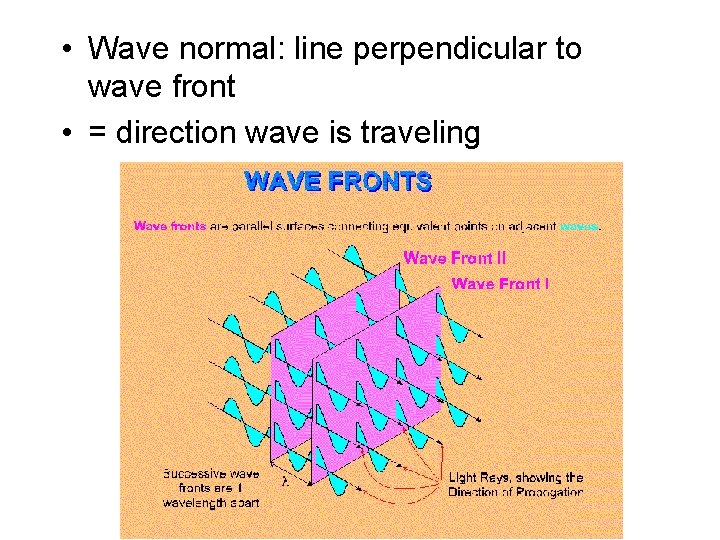
• Wave: single pulse of energy advancing • Wave front: surface through all similar points on adjacent waves

• Wave normal: line perpendicular to wave front • = direction wave is traveling

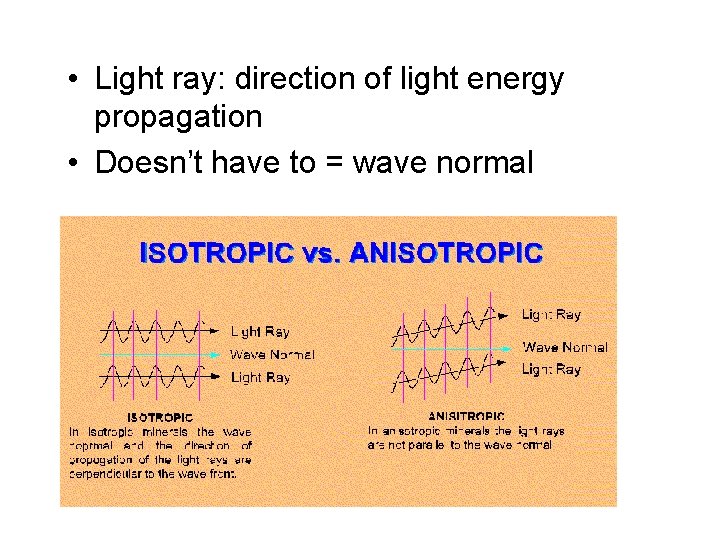
• Light ray: direction of light energy propagation • Doesn’t have to = wave normal

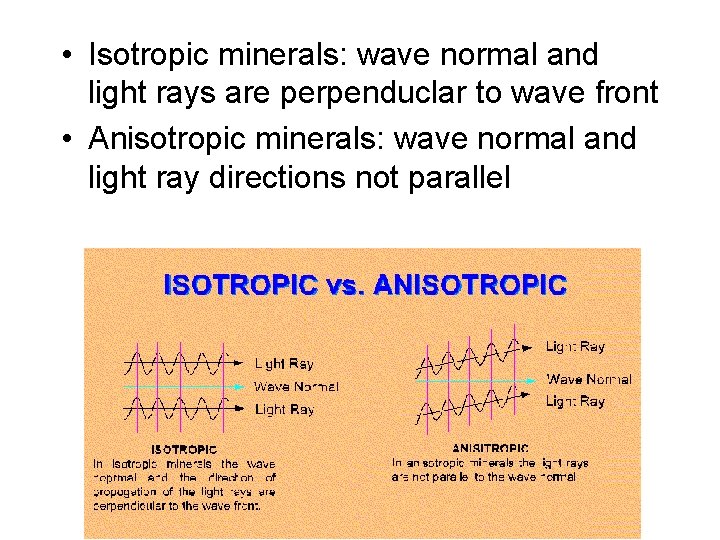
• Isotropic minerals: wave normal and light rays are perpenduclar to wave front • Anisotropic minerals: wave normal and light ray directions not parallel

• Two wave vibrating in same plane, traveling on same path will interfere • Retardation ( ): distance that one wave lags behind the other

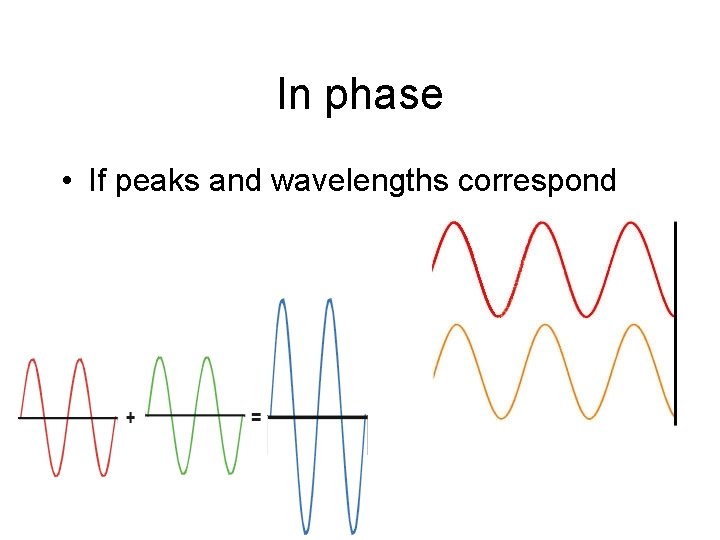
In phase • If peaks and wavelengths correspond

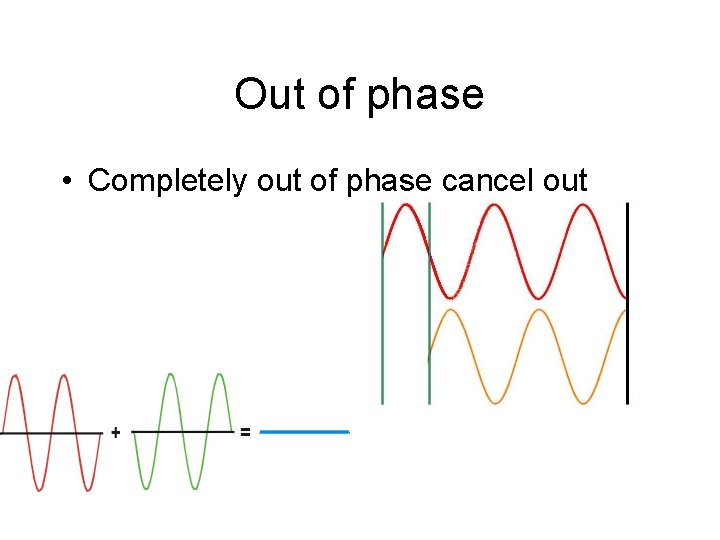
Out of phase • Completely out of phase cancel out

Partially out of phase

What happens as light moves through the scope? your eye amplitude, A wavelength, light ray light travels as waves I = f(A) waves travel from source to eye light source Frequency = # of waves/sec to pass a given point (hz) f = v/ © Jane Selverstone, University of New Mexico, 2003 v = velocity (in physics v = c, but no longer)

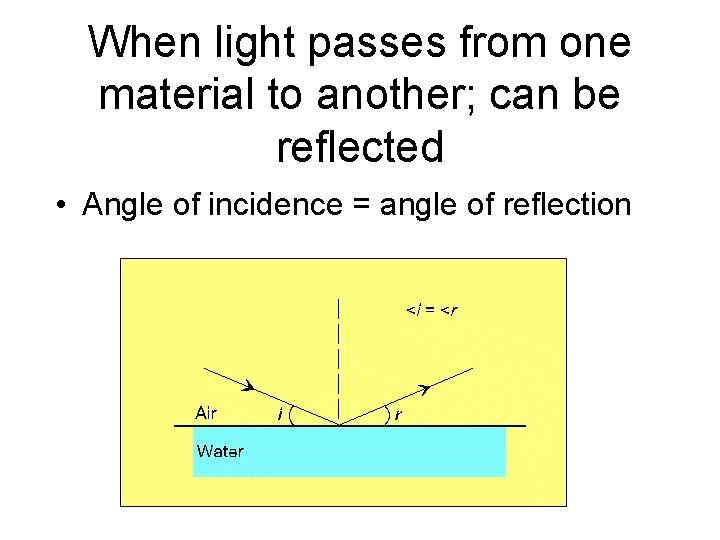
When light passes from one material to another; can be reflected • Angle of incidence = angle of reflection

When light passes from one material to another; can be refracted • Index of refraction: how bent the light is passing through a material • High index = low velocity

Light from the sun: • Vibrates in all directions, perp. To direction of propagation • Unpolarized light

Light in microscope: • Polarized light • Vibration constrained to one direction

Effect of polarization: • Polarized light • Vibration constrained to one direction

What happens as light moves through the scope? Each photon vibrates as a wave form in a single plane propagation direction Light beam = numerous photons, all vibrating in the same planes of vibration directions Polarized Light beam = numerous photons, each vibrating in a different plane Vibration in all directions ~ perpendicular to propagation direction Unpolarized Light

How to polarize light: • Polarizer sheets

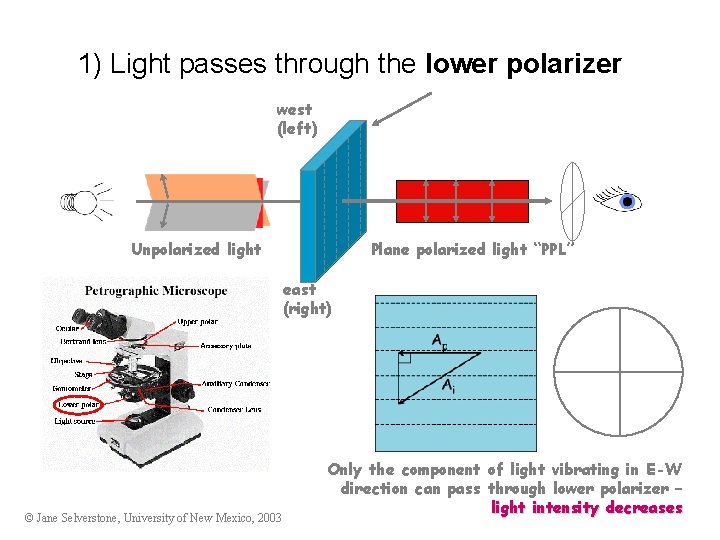
1) Light passes through the lower polarizer west (left) Unpolarized light Plane polarized light “PPL” east (right) © Jane Selverstone, University of New Mexico, 2003 Only the component of light vibrating in E-W direction can pass through lower polarizer – light intensity decreases

2) Insert the upper polarizer west (left) north (back) east (right) south (front) Black!! (“extinct”) Now what happens? What reaches your eye? Why would anyone design a microscope that prevents light from reaching your eye? ? ? XPL=crossed nicols (crossed polars) © Jane Selverstone, University of New Mexico, 2003

Crossed-polars

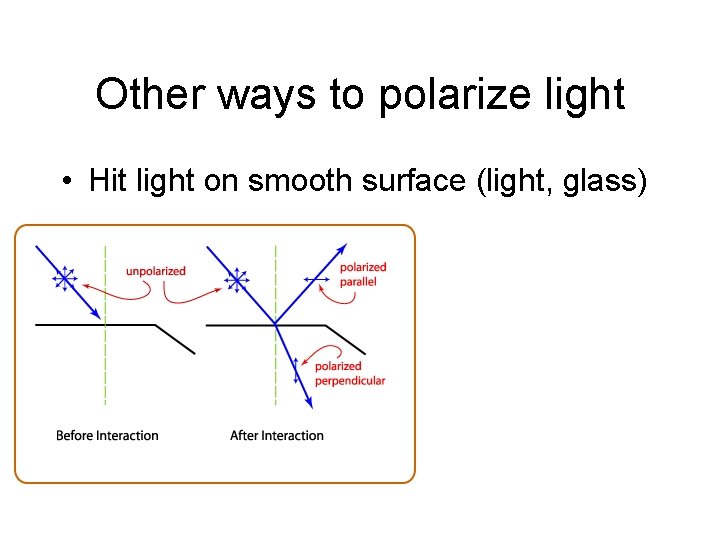
Other ways to polarize light • Hit light on smooth surface (light, glass)

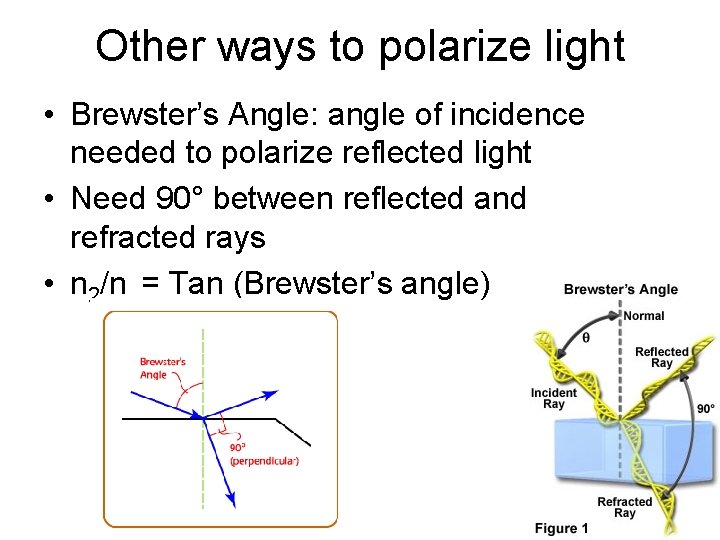
Other ways to polarize light • Brewster’s Angle: angle of incidence needed to polarize reflected light • Need 90° between reflected and refracted rays • n 2/n = Tan (Brewster’s angle)

• Brewster’s angle is reason polarized sunglasses work so well • Ever turn your head 90° wearing polarized sunglasses?