Optical Fiber Communications Chapter 3 Attenuation and Dispersion

Overview – Chapter 3 3. 1 Attenuation 3. 2 Signal Dispersion in Fibers 3. 3 Characteristics of Single-Mode Fibers 3. 4 International Standards 3. 5 Specialty Fibers 2

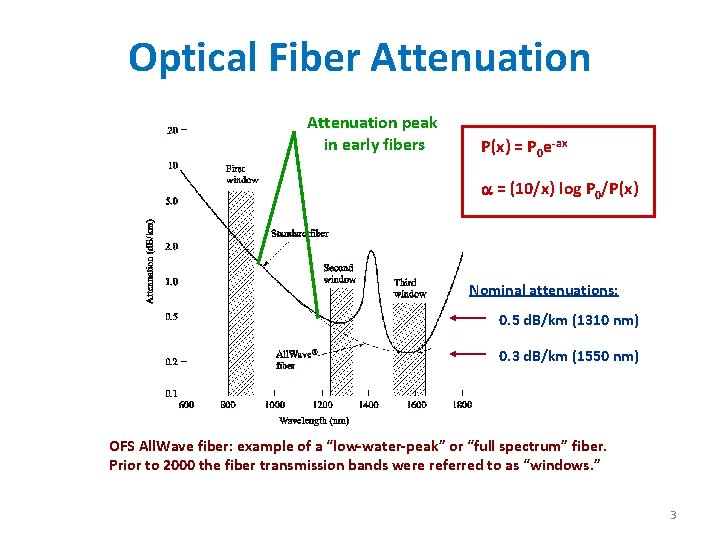
Optical Fiber Attenuation peak in early fibers P(x) = P 0 e-ax a = (10/x) log P 0/P(x) Nominal attenuations: 0. 5 d. B/km (1310 nm) 0. 3 d. B/km (1550 nm) OFS All. Wave fiber: example of a “low-water-peak” or “full spectrum” fiber. Prior to 2000 the fiber transmission bands were referred to as “windows. ” 3

The d. Bm Unit 4

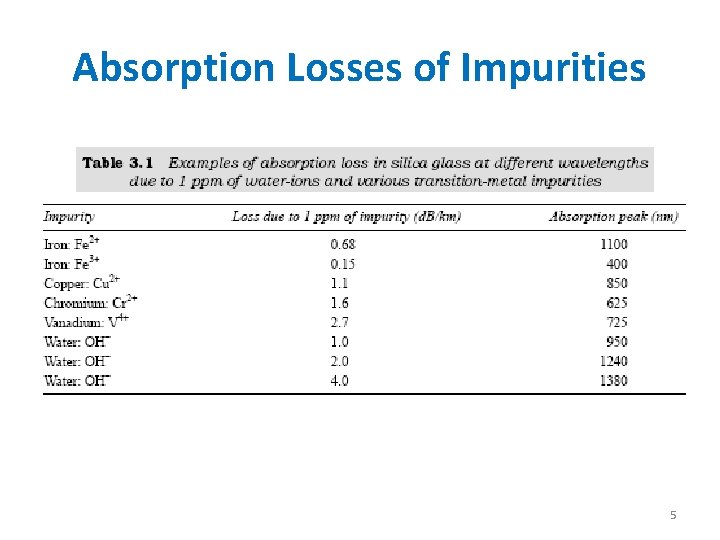
Absorption Losses of Impurities 5

Bending Losses in Fibers (1) • Optical power escapes from tightly bent fibers • Bending loss increases at longer wavelengths – Typical losses in 3 loops of standard 9 - m single-mode fiber (from: Lightwave; Feb 2001; p. 156): R – 2. 6 d. B at 1310 nm and 23. 6 d. B at 1550 nm for R = 1. 15 cm – 0. 1 d. B at 1310 nm and 2. 60 d. B at 1550 nm for R = 1. 80 cm • Progressively tighter bends produce higher losses • Bend-loss insensitive fibers have been developed and now are recommended • Improper routing of fibers and incorrect storage of slack fiber can result in violations of bend radius rules Test setup for checking bend loss: N fiber loops on a rod of radius R 6

Bending Losses in Fibers (2) The total number of modes that can be supported by a curved fiber is less than in a straight fiber. 7

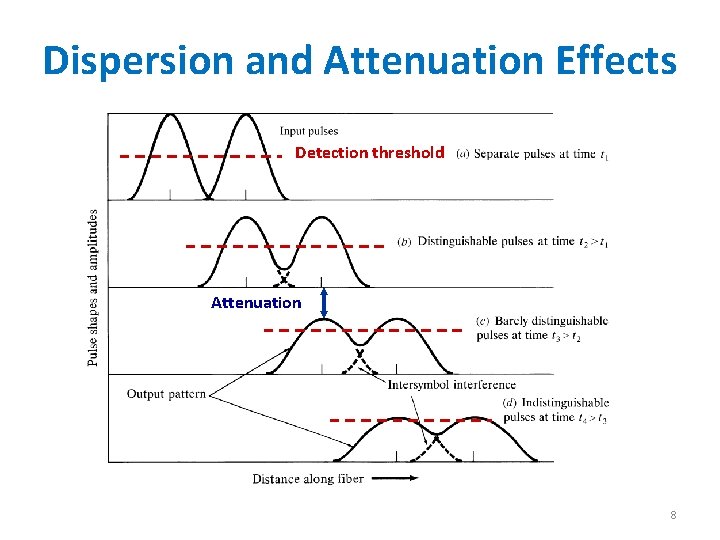
Dispersion and Attenuation Effects Detection threshold Attenuation 8

Factors Contributing to Dispersion (1) • The wave propagation constant β is a slowly varying function of the angular frequency ω. • One can see where various dispersion effects arise by expanding β in a Taylor series about a central frequency ω0. 1. The 1 st term β 0 z describes a phase shift of the optical wave. 2. The factor β 1(ω0)z produces a group delay tg = z/Vg 9

Factors Contributing to Dispersion (2) 3. The factor β 2 shows that the group velocity of a monochromatic wave depends on the wave frequency. • Thus the different group velocities of the frequency components of a pulse cause it to broaden with distance. • The group velocity spreading is the GVD • The dispersion D is related to β 2 by 4. The factor β 3 is the third-order dispersion. – The third-order dispersion can be related to the dispersion D and the dispersion slope S 0 = ∂D/∂λ (the variation in the dispersion D with wavelength) 10

Chromatic Dispersion (CD) • It also is known as intramodal dispersion • This pulse spreading is known as the group velocity dispersion (GVD) – It is pulse spreading that occurs within a single mode, because the GVD is a function of wavelength – Since CD depends on wavelength, its effect on signal distortion increases with source spectral width • The dispersion is given in units of ps/(nm × km) LED Laser 11

$Material Dispersion Material dispersion occurs because the index of refraction varies as a function$

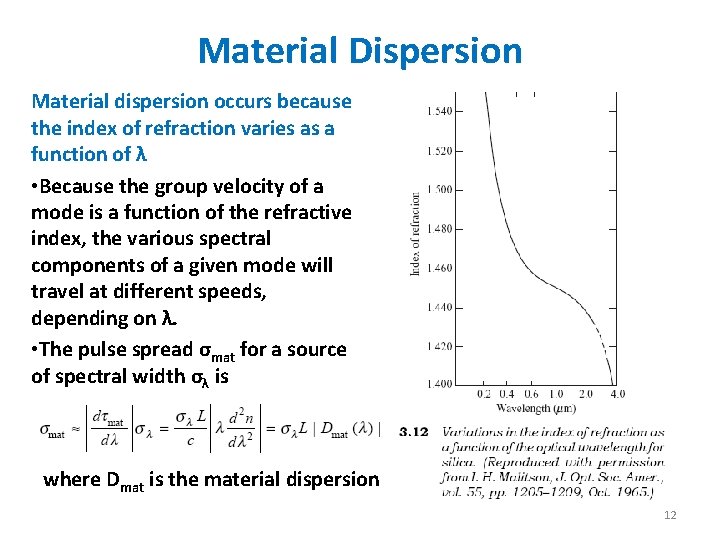
Material Dispersion Material dispersion occurs because the index of refraction varies as a function of λ • Because the group velocity of a mode is a function of the refractive index, the various spectral components of a given mode will travel at different speeds, depending on λ. • The pulse spread σmat for a source of spectral width σλ is where Dmat is the material dispersion 12

Material Dispersion Comparison LED source Laser diode source 13

Polarization-Mode Dispersion • A varying birefringence along its length will cause each polarization mode to travel at a slightly different velocity. • The difference in propagation times ΔτPMD between the two orthogonal polarization modes will result in pulse spreading. • This is the polarization-mode dispersion (PMD) • PMD is a random, time-varying function in a fiber, so it needs to be measured statistically. • If DPMD, which is measured in ps/(km)0. 5, is the average PMD parameter, then Typical values of DPMD range from 0. 05 to 1. 0 ps /(km)0. 5. 14

Dispersion Calculation • The broadening σ of an optical pulse over a fiber of length L is given by σ = D(λ)σλ , where σλ is the half-power spectral width of the optical source. • For a non-dispersion shifted fiber For a dispersion shifted fiber: D(λ) = (λ – λ 0)S 0. S 0 is the dispersion slope S(λ) = d. D/dλ at λ 0, given in ps/(nm 2 • km). 15

Dispersion Comparisons for NZDS Fiber 16

ITU-T Recommendations for Fibers (2) 17

ITU-T Recommendations for Fibers (1) 18

Multimode Fiber Transmission Distances • The possible transmission distances when using fibers with different core sizes and bandwidths for Ethernet, Fibre Channel, and SONET/SDH applications. 19

Examples of Specialty Fibers 20