Optical Fiber Communications Chapter 2 Optical Fibers Structures

Optical Fiber Communications Chapter 2 Optical Fibers: Structures, Waveguiding, and Fabrication

Overview – Chapter 2 2. 1 The Nature of Light 2. 2 Basic Optical Laws and Definitions 2. 3 Optical Fiber Modes and Configurations 2. 4 Mode Theory for Circular Waveguides 2. 5 Single-Mode Fibers 2. 6 Graded-Index Fiber Structure 2. 7 Fiber Materials 2. 8 Photonic Crystal Fibers 2. 9 Fiber Fabrication 2. 10 Mechanical Properties of Fibers 2. 11 Fiber Optic Cables 2. 12 Cable Installation Methods 2

2. 1 The Nature of Light The electric or magnetic field of plane linearly polarized waves traveling in a direction k, where the wave vector k = 2π/λ is the wave propagation constant: A linearly polarized wave with polarization vector ex is 3

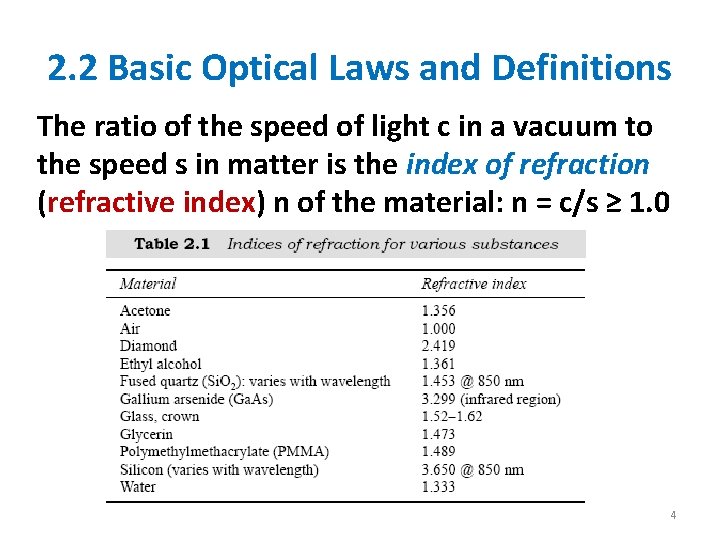
2. 2 Basic Optical Laws and Definitions The ratio of the speed of light c in a vacuum to the speed s in matter is the index of refraction (refractive index) n of the material: n = c/s ≥ 1. 0 4

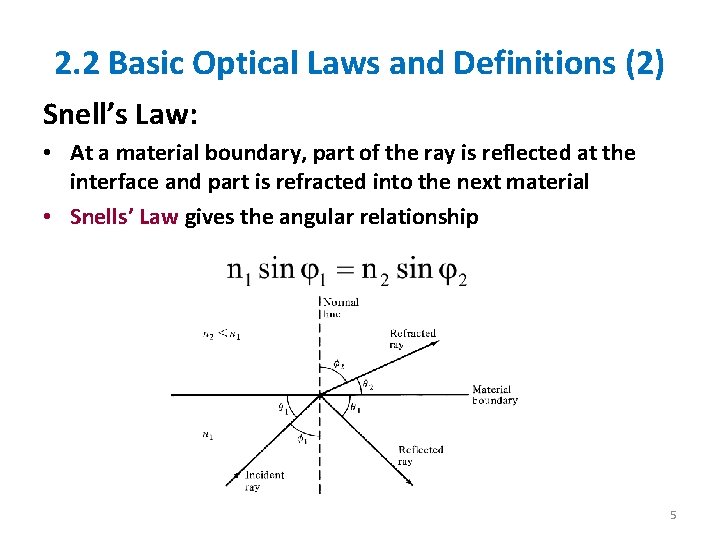
2. 2 Basic Optical Laws and Definitions (2) Snell’s Law: • At a material boundary, part of the ray is reflected at the interface and part is refracted into the next material • Snells’ Law gives the angular relationship 5

2. 2 Basic Optical Laws and Definitions (3) Applications of Snell’s Law 6

2. 3 Optical Fiber Modes and Configurations (1) • In step-index fibers the core of radius a has a refractive index n 1, which is typically equal to 1. 48. This is surrounded by a cladding of slightly lower index n 2 = n 1(1 - Δ). • Δ is the core-cladding index difference or the index difference. Typical Δ values range from 1 -3 % for multimode fibers and from 0. 2 -1. 0 % for single-mode fibers. 7

Optical Fiber Type Comparisons • The indices are uniform in a step-index fiber • The index varies with the core radius in a gradedindex fiber Typical diameters SM core: 8 -10 m SM cladding: 125 m MM core: 50 or 62. 5 m MM cladding: 125 m (SM = single mode) (MM = multimode) Cladding 2 a 2 a Core n 1 n 2 Step-index fiber n 1 n 2 n 1 Graded-index fiber (a) Basic fiber types (b) Sample tailored profiles 8

Propagating Rays in Fibers Propagation mechanism in an ideal step-index waveguide • Light enters the core at an angle θ 0 from a medium of index n • Propagating rays are totally internally reflected at core/clad interface • Meridional rays follow a zig-zag path along the fiber core • These rays pass through the fiber axis after each reflection • Snell’s law determines the minimum angle for total internal reflection 9

Numerical Aperture • From Snell’s law, the minimum angle for total internal reflection is sin min = sin c = n 2/n 1 • This condition is related to the maximum entrance angle θ 0, max = θA (acceptance angle) by the relationship where θc = /2 - c [recall that sin x = (1 – cos 2 x)1/2 ] This equation defines the numerical aperture NA: NA = n sin θA = (n 12 – n 22)1/2 n 1 (2Δ) 1/2 10

Numerical Aperture Example 11

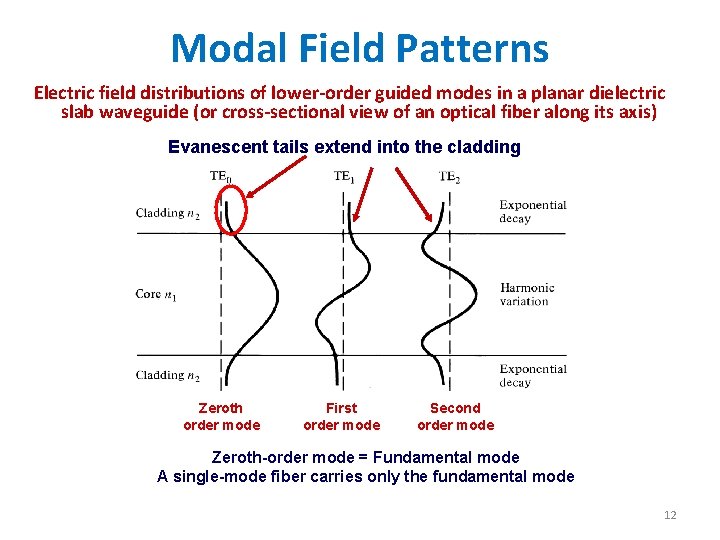
Modal Field Patterns Electric field distributions of lower-order guided modes in a planar dielectric slab waveguide (or cross-sectional view of an optical fiber along its axis) Evanescent tails extend into the cladding Zeroth order mode First order mode Second order mode Zeroth-order mode = Fundamental mode A single-mode fiber carries only the fundamental mode 12

V Number Definition • An important parameter connected with the cutoff condition is the V number defined by 13

Number of Modes in a Fiber V can be used to express the number of modes M in a multimode step-index fiber when V is large 14

2. 5 Single-Mode Fibers Single-mode fiber features: • The dimension of the core diameter is a few wavelengths (usually 8– 12) • The index difference between the core and the cladding is small (0. 2 to 1. 0 %) • The core diameter is just below the cutoff of the first higher-order mode: V < 2. 405 15

Mode Field Diameter • The mode-field diameter (MFD) can be determined from the mode-field distribution of the fundamental fiber mode and is a function of the optical source wavelength • The MFD is used to predict fiber splice loss, bending loss, cutoff wavelength, and waveguide dispersion • To find MFD: (a) measure the far-field intensity distribution E 2(r) (b) calculate the MFD using the Petermann II equation 16

2. 6 Graded-Index Fiber Structure • The core index decreases with increasing distance r from the center of the fiber but is generally constant in the cladding. • The most commonly used construction for the refractive-index variation in the core is the power law relationship: A typical value of α is 2. 0 The local numerical aperture is defined as 17

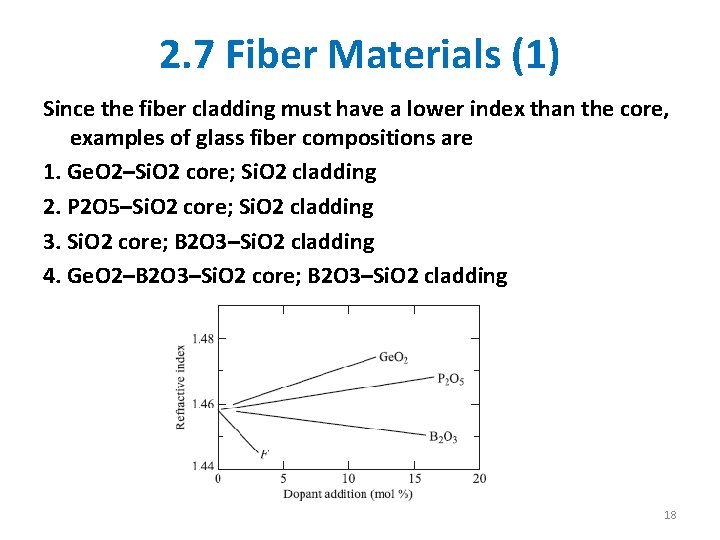
2. 7 Fiber Materials (1) Since the fiber cladding must have a lower index than the core, examples of glass fiber compositions are 1. Ge. O 2–Si. O 2 core; Si. O 2 cladding 2. P 2 O 5–Si. O 2 core; Si. O 2 cladding 3. Si. O 2 core; B 2 O 3–Si. O 2 cladding 4. Ge. O 2–B 2 O 3–Si. O 2 core; B 2 O 3–Si. O 2 cladding 18

2. 7 Fiber Materials (2) The growing demand for delivering high-speed services directly to the workstation has led to highbandwidth graded-index polymer (plastic) optical fibers (POF) for use in a customer premises 19

2. 8 Photonic Crystal Fibers (PCF) • The core regions of a PCF contain air holes, which run along the entire length of the fiber • The PCF microstructure offers extra dimensions in controlling effects such as dispersion, nonlinearity, and birefringence • The two basic PCF categories are index-guiding fibers (left) and photonic bandgap fibers (right) 20

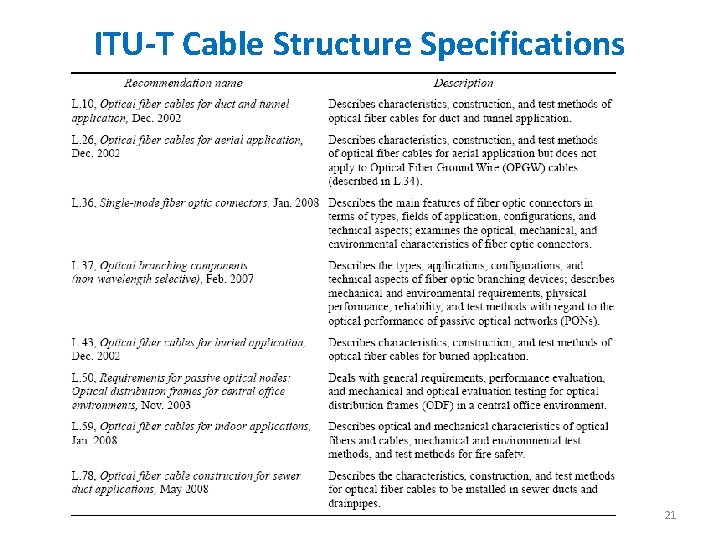
ITU-T Cable Structure Specifications 21

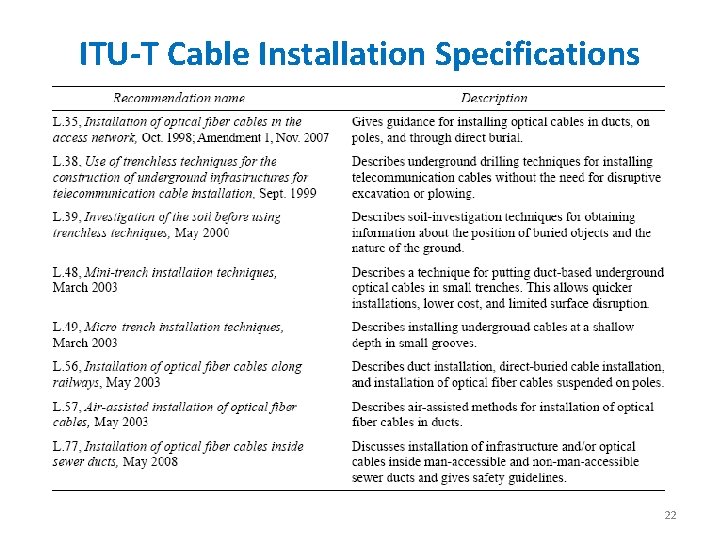
ITU-T Cable Installation Specifications 22