Optical Fiber Communication Lecture 2 Nature of light

Optical Fiber Communication Lecture 2: Nature of light and Ray theory Dr. Ghusoon Mohsin Ali M. Sc. in Electronics & Communication Department of Electrical Engineering College of Engineering Al-Mustansiriya University 1

Laws of Reflection & Refraction When a ray is incident on the interface between two dielectrics of different refractive indices (e. g. glass-air), reflection and refraction occur. Reflection law: angle of incidence=angle of reflection Figure 2. 5 Refraction of light at a media interface Snell’s law of refraction:

ØIf n 2 < n 1 , then the angle of refraction is greater than the angle of incidence and the refracted ray is said to have moved away from the normal. ØIf the angle of incidence (ϕ 1) is increased further, the angle of refraction (ϕ 2) also increases in accordance with the Snell’s law and at a particular angle of incidence the angle of refraction becomes 90 o and the refracted ray grazes along the media interface. Ø This angle of incidence is called the critical angle of incidence (θc) of medium 2 with respect to medium 1. One should note here that critical angle is media-relative. ØIf (ϕ 1) is increased beyond the critical angle, there exists no refracted ray and the incident light ray is then reflected back into the same medium. This phenomenon is called the total internal reflection of light.

ØThe word ‘total’ signifies that the entire light energy that was incident on the media interface is reflected back into the same medium. Total Internal Reflection (TIR) obeys the laws of reflection of light. ØThis phenomenon shows that light energy can be made to remain confined in the same medium. Thus we can see that there are two basic requirements for a TIR to occur: 1. The medium from which light is incident, must be optically denser than the other medium. In figure 2. 5 n 2 < n 1. 2. The angle of incidence in the denser medium must be greater than the critical angle.
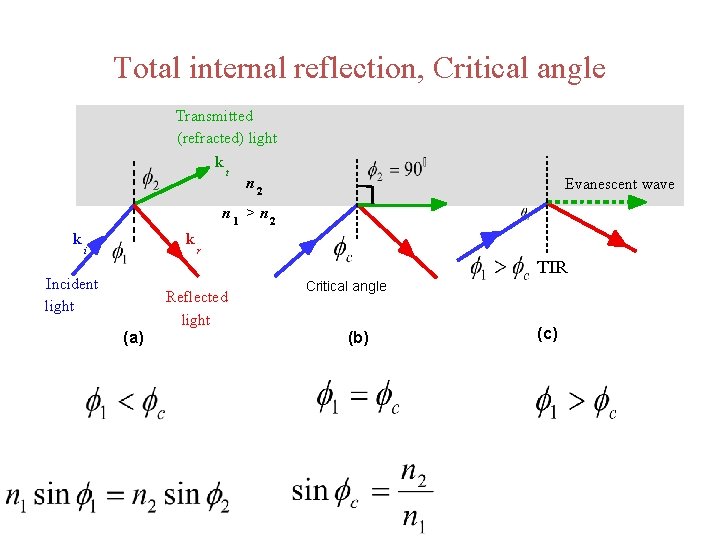
Total internal reflection, Critical angle Transmitted (refracted) light k t n 2 Evanescent wave n 1 > n 2 k k i Incident light (a) r Reflected light TIR Critical angle (b) (c)

LAUNCHING OF LIGHT INTO AN OPTICAL FIBER ØLight propagates inside an optical fiber by virtue of multiple TIRs at the corecladding interface. ØThe refractive index of the core glass is greater than that of the cladding. This meets the first condition for a TIR. Ø All the light energy that is launched into the optical fiber through its tip does not get guided along the fiber. Only those light rays propagate through the fiber which are launched into the fiber at such an angle that the refracted ray inside the core of the optical fiber is incident on the core-cladding interface at an angle greater than the critical angle of the core with respect to the cladding. Figure 2. 8: Launching of Meridional Rays
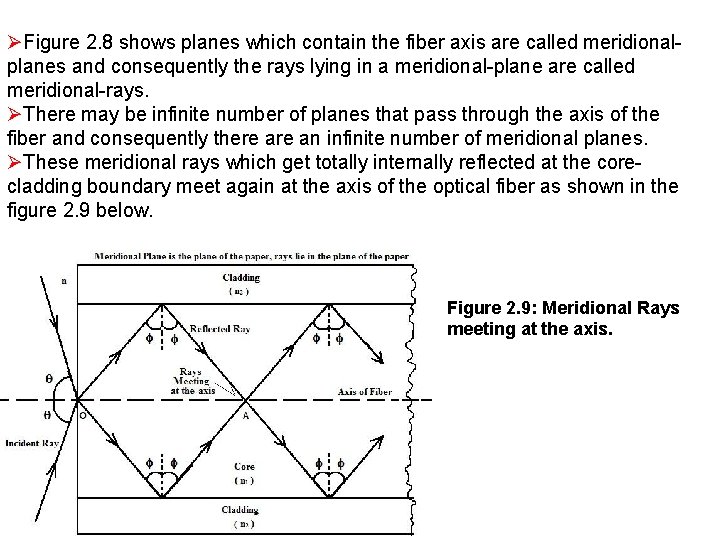
ØFigure 2. 8 shows planes which contain the fiber axis are called meridionalplanes and consequently the rays lying in a meridional-plane are called meridional-rays. ØThere may be infinite number of planes that pass through the axis of the fiber and consequently there an infinite number of meridional planes. ØThese meridional rays which get totally internally reflected at the corecladding boundary meet again at the axis of the optical fiber as shown in the figure 2. 9 below. Figure 2. 9: Meridional Rays meeting at the axis.
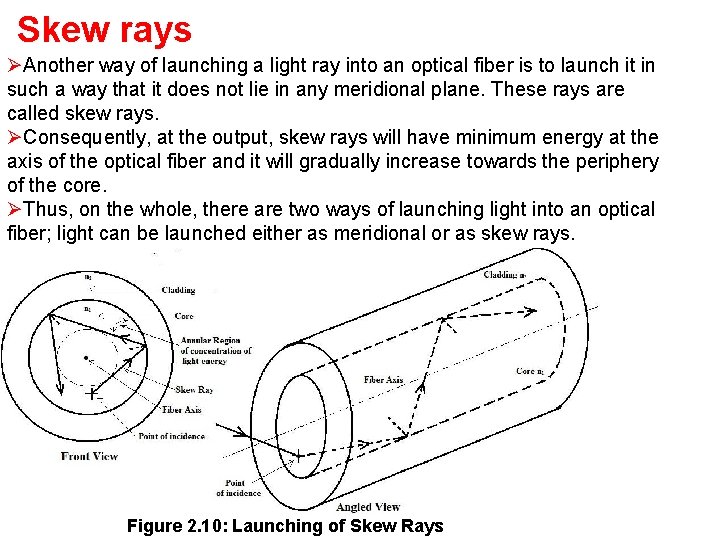
Skew rays ØAnother way of launching a light ray into an optical fiber is to launch it in such a way that it does not lie in any meridional plane. These rays are called skew rays. ØConsequently, at the output, skew rays will have minimum energy at the axis of the optical fiber and it will gradually increase towards the periphery of the core. ØThus, on the whole, there are two ways of launching light into an optical fiber; light can be launched either as meridional or as skew rays. Figure 2. 10: Launching of Skew Rays
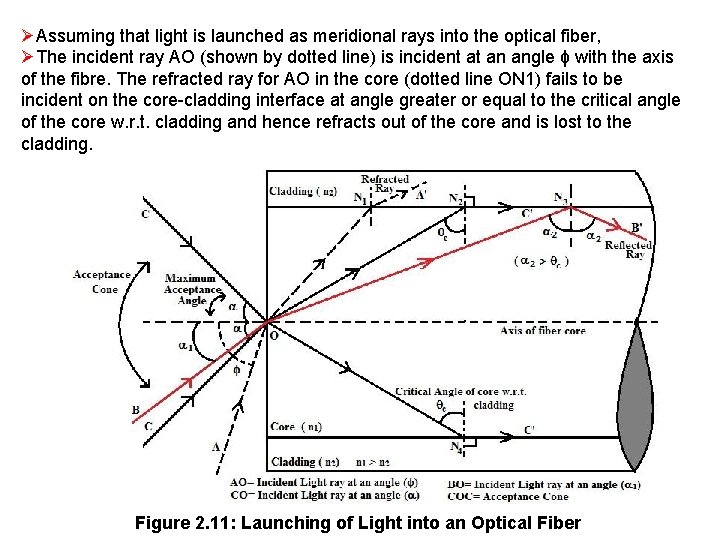
ØAssuming that light is launched as meridional rays into the optical fiber, ØThe incident ray AO (shown by dotted line) is incident at an angle ϕ with the axis of the fibre. The refracted ray for AO in the core (dotted line ON 1) fails to be incident on the core-cladding interface at angle greater or equal to the critical angle of the core w. r. t. cladding and hence refracts out of the core and is lost to the cladding. Figure 2. 11: Launching of Light into an Optical Fiber

ØThe ray CO is launched into the fiber at such an angle ‘α’ that its refracted ray is incident at the core-cladding boundary at its critical angle ‘θc’. ØIf any light ray is launched at an Fiber Optic angle more than α then the refracted ray just refracts out to the cladding because the angle of incidence of its refracted ray at the corecladding interface is less than the critical angle. ØThus the angle α is indicative of the maximum possible angle of launching of a light ray that is accepted by the fiber. ØConsequently, the angle α is called the angle of acceptance of the fiber core. ØSince the optical fiber is symmetrical about its axis, it is very clear that all the launched rays, which make an angle α with the axis, considered together, form a sort of a cone. ØThis cone is called the acceptance cone.

NUMERICAL APERTURE OF OPTICAL FIBER ØAn incident ray AO is incident from medium 1 at the tip of the fiber making an angle α with the axis of the fiber, which is the acceptance angle of the fibre. ØThe refracted ray for this incident ray in the core then is incident at the corecladding interface at the critical angle θc of the core with respect to the cladding. The angle of refraction for critical angle of incidence is 900 and the refracted ray thus grazes along the core-cladding boundary along BC as shown in the figure 2. 12. Figure 2. 12: Launching of Light into an Optical Fiber

ØAccording Snell’s laws, the incident and the refracted rays lie in the same meridional plane, which is the plane of the paper in this case. Applying Snell’s law at the medium 1 -core interface we get: (2. 1) From the figure it is clear that, (2. 1), we get: substituting this in equation (2. 2) From the basic trigonometric ratios, (2. 3) Applying Snell’s law at the core-cladding interface we get:

(2. 4) Substituting equation (2. 4) in equation (2. 2) we get: ØSince the initial medium 1 from which the light is launched is air most of the times, n = 1. The angle α is indicative of light accepting capability of the optical fiber. ØGreater the value of α, more is the light accepted by the optical fiber. In other words, the optical fiber acts as some kind of aperture that accepts only some amount of the total light energy incident on it. The light accepting efficiency of this aperture is thus indicated by sin α and hence this quantity is called as the numerical aperture (N. A. ) (2. 5)

relative refractive index Δ

H. W

ØNumerical Aperture indicates the light collecting efficiency of an optical fiber. More the value of N. A. better is the fiber. Ø For greater values of N. A, either the refractive index of the core (n 1) has to be increased or the refractive index of the cladding (n 2) has to be reduced. Since the value of its refractive index n 1 is thus fixed (approximately 1. 5). The only option thus available with us is to reduce the value of n 2. But the lowest value of 1 for air because till date no material is known which has a refractive index lower than that. If we make n 2 =1, we would then get the maximum possible N. A. for an optical fiber. But then we are basically talking about removing the cladding because. Thus one can clearly say that from the point of view of light accepting efficiency, the presence of a cladding is undesirable. ØHowever, on optical fibers is not just to put light inside an optical fiber with the best efficiency but also to propagate the light over long distances with the least attenuation. ØIn other words, light launching efficiency is just one of the key characteristic aspects of an optical fiber. There are other attributes too which have to be given importance while determining the quality of an optical fiber. One of such attributes of an optical fiber is its bandwidth. Large bandwidths are desirable for high data rates of transmission.
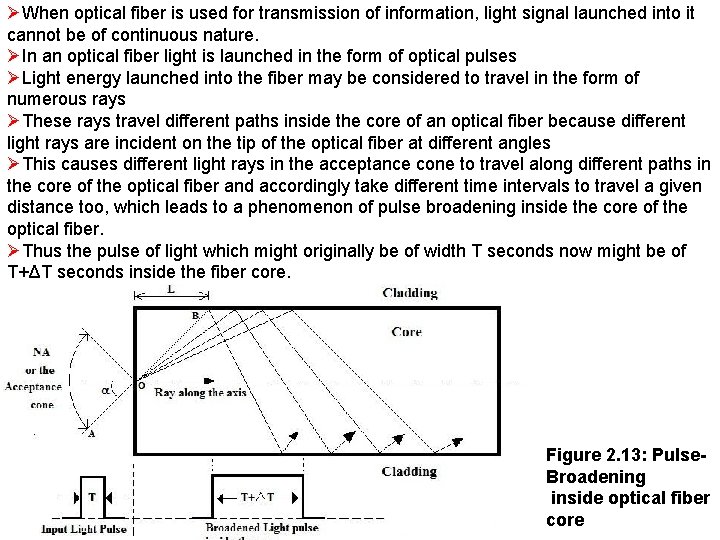
ØWhen optical fiber is used for transmission of information, light signal launched into it cannot be of continuous nature. ØIn an optical fiber light is launched in the form of optical pulses ØLight energy launched into the fiber may be considered to travel in the form of numerous rays ØThese rays travel different paths inside the core of an optical fiber because different light rays are incident on the tip of the optical fiber at different angles ØThis causes different light rays in the acceptance cone to travel along different paths in the core of the optical fiber and accordingly take different time intervals to travel a given distance too, which leads to a phenomenon of pulse broadening inside the core of the optical fiber. ØThus the pulse of light which might originally be of width T seconds now might be of T+ΔT seconds inside the fiber core. Figure 2. 13: Pulse. Broadening inside optical fiber core

ØThe amount of broadening is measured in terms of the increase in the pulse time width and is denoted by ΔT. the value of ΔT is given by: (2. 6) Where, ΔT= Pulse Broadening; c = velocity of light in free space; n 1 = refractive index of core and n 2 = refractive index of the cladding. The quantity L is the horizontal distance travelled before suffering the first total internal reflection by the refracted ray OB which corresponds to the incident ray AO, incident at the acceptance angle as shown in the figure. ØThe amount of pulse broadening is effectively the difference in time of travel between the ray travelling along the axis and the incident ray AO. ØThis pulse broadening effect signifies that if a second pulse is now launched into the fiber within the time interval T+ΔT, the two pulses will overlap and no identifiable data would be obtained on the output. ØThus for a given length L, there would be a corresponding value of ΔT (from equation 2. 6) which would limit the rate at which light pulses can be launched into the optical fiber.

This indirectly limits the bandwidth available on the fiber. Thus we can say that more the pulse broadening lower the bandwidth. That is: (2. 7) ØIn equation 2. 6, we see that the value of ΔT is dependent on the value of L, the difference (n 1 – n 2) as well as the value of n 1/n 2. ØBut reducing the value of L would signify the reduction in the length of the optical fiber, which is not desirable. ØAs 1<n 2<n 1, the ratio, n 1 / n 2 is very close to 1. ØThus for low ΔT values, the only option available with us is to decrease the value (n 1–n 2) or in other words, to increase the refractive index of the cladding n 2. ØOne can now notice that a contradictory situation has been generated as to whether the cladding should be removed for high NA or to use a cladding of large refractive index value for higher bandwidth? The answer to this query is purely application specific. ØThat means if an optical fiber is used as a sensor (say), where lowest possible light has to be accepted, we use fiber with low n 2 values. ØWhen the optical fiber is used for data communication, fibers with high values of n 2 are used. For practical communication purposes the value of (n 1 – n 2) is made of the order of about 10 -3 to 10 -4. If the cladding is removed, the value of n 2 becomes 1 and the value of the above difference becomes about 0. 5. The bandwidth corresponding to this value of n 1 -n 2 is of the order of few Kilohertz, which is far worse than that of a normal twisted pair of wires.
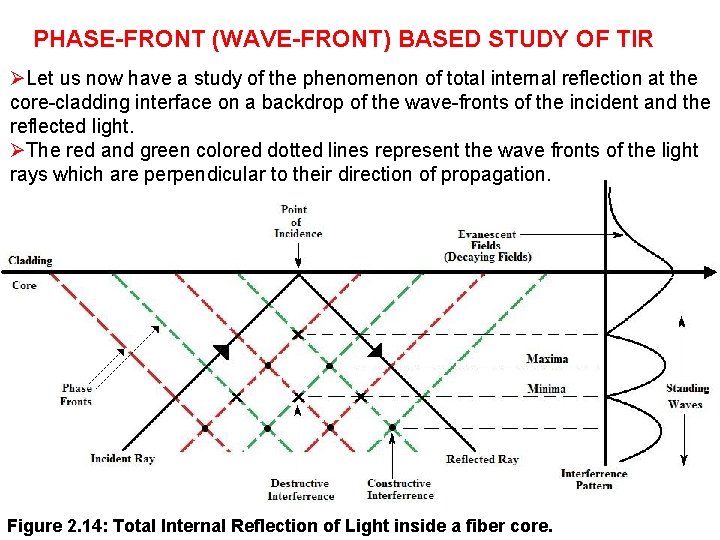
PHASE-FRONT (WAVE-FRONT) BASED STUDY OF TIR ØLet us now have a study of the phenomenon of total internal reflection at the core-cladding interface on a backdrop of the wave-fronts of the incident and the reflected light. ØThe red and green colored dotted lines represent the wave fronts of the light rays which are perpendicular to their direction of propagation. Figure 2. 14: Total Internal Reflection of Light inside a fiber core.

ØThus, when two similar colored wave-fronts meet, they interfere constructively and dissimilar colored wave-fronts interfere destructively. ØIn the core, the interference between the incident and the reflected wave-fronts constitutes a standing wave pattern of varying light intensity with discrete maxima and minima in a direction normal to the core-cladding interface. ØTotal internal reflection is also accompanied by an abrupt phase change between the incident and the reflected rays at the corecladding boundary. This phase change depends on the angle of incidence of the incident ray at the core-cladding boundary, the refractive index or the core and cladding and various other parameters. ØIf we refer to the electromagnetic wave theory of light, it shows that at total internal reflection, the light intensity inside the cladding is not completely zero. ØInstead, there exist some decaying fields in the cladding, which do not carry any power but support the total internal reflection phenomenon

ØThese fields are called as evanescent fields. ØThe importance of these evanescent fields in the TIR is that even the slightest disturbance to these fields in the cladding could lead to the failure of the TIR at the core-cladding boundary accompanied by leakage of optical power to the cladding. ØThis is one of the instances when the ray-model of light becomes inadequate in explaining the phenomena exhibited by light. ØThe evanescent fields are decaying fields, ØLarger the value of the angle of incidence of the incident ray at the core-cladding boundary, sharper is the decay of the evanescent fields. ØThus there must me a sufficient thickness of cladding provided for these evanescent fields to be accommodated so that they decay to a negligibly small value in the cladding and cannot be disturbed by external sources.
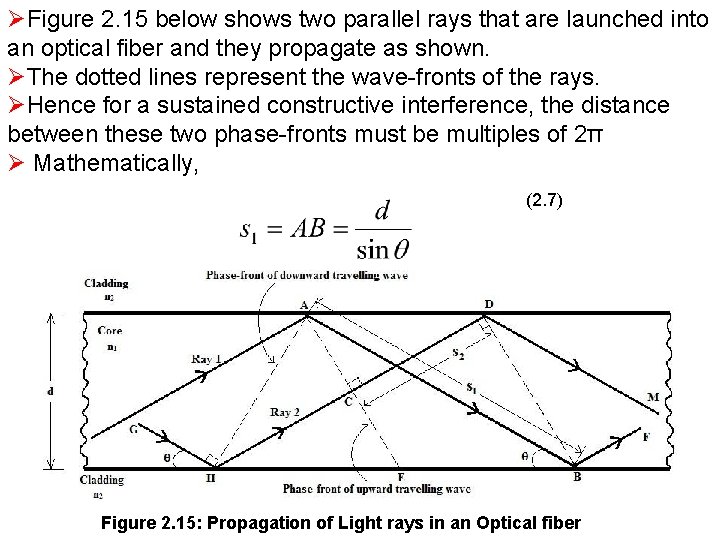
ØFigure 2. 15 below shows two parallel rays that are launched into an optical fiber and they propagate as shown. ØThe dotted lines represent the wave-fronts of the rays. ØHence for a sustained constructive interference, the distance between these two phase-fronts must be multiples of 2π Ø Mathematically, (2. 7) Figure 2. 15: Propagation of Light rays in an Optical fiber

(2. 8) If δ is the phase change undergone in each TIR of Ray 1, interfere constructively if phase difference is 2π x integer For a sustained constructive interference, a phase difference must have of either 0 or integral multiples of 2π. That is, for an integer m (=0, 1, 2, 3, …) the following condition must be satisfied: (2. 9) (2. 10)

ØThe significance of the equation 2. 10 is that only those rays, which are incident on the tip of the fiber at angles such that their angle of refraction in the core satisfies equation (2. 10), can successfully travel along the fiber. If we concentrate on equation (2. 10), we find that since ‘m’ can take only discrete integral values, the value of angle θ is also discrete. ØThis suggests that there are only some discrete launching angles within the acceptance cone (N. A. cone) for which the rays can propagate inside the fiber core. ØThus the condition that the launching angle of the incident ray should be within the acceptance cone is necessary but not sufficient. Ø Any ray that is not launched at these discrete angles will not propagate inside the optical fiber. ØThis discretization in the values of launching angles lead to formation of what are called as modes in an optical fiber, which are nothing but different patterns of light intensity distribution around the axis of the core.
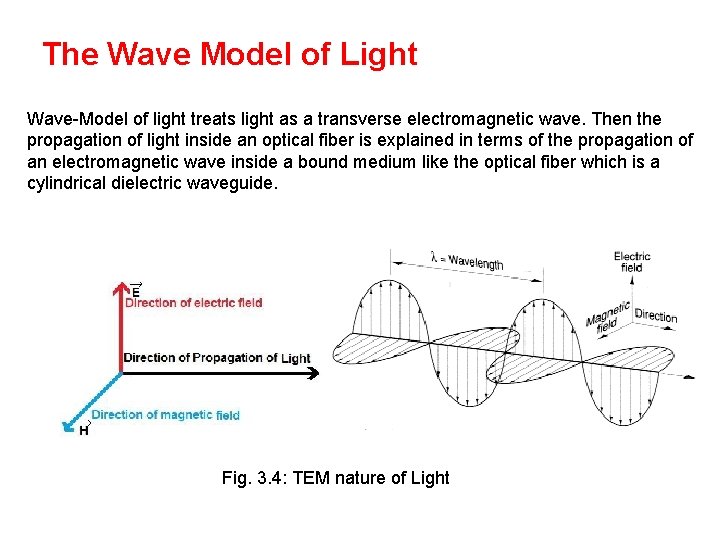
The Wave Model of Light Wave-Model of light treats light as a transverse electromagnetic wave. Then the propagation of light inside an optical fiber is explained in terms of the propagation of an electromagnetic wave inside a bound medium like the optical fiber which is a cylindrical dielectric waveguide. Fig. 3. 4: TEM nature of Light

Unguided electromagnetic waves in free space, can be described as a superposition of plane waves; these can be described as TEM modes. However in any sort of waveguide where boundary conditions are imposed by a physical structure, a wave of a particular frequency can be described in terms of a transverse mode (or superposition of such modes). These modes generally follow different propagation constants. Modes in waveguides can be further classified as follows: ØTransverse electromagnetic (TEM) modes: neither electric nor magnetic field in the direction of propagation (Ez=0 and Hz=0), . . ØTransverse electric (TE) modes: no electric field in the direction of propagation. ( Ez=0), These are sometimes called H modes because there is only a magnetic field along the direction of propagation (H is the conventional symbol for magnetic field). ØTransverse magnetic (TM) modes: no magnetic field in the direction of propagation ( Hz=0), . These are sometimes called E modes because there is only an electric field along the direction of propagation. ØHybrid modes: non-zero electric and magnetic fields in the direction of propagation (Ez≠ 0 and Hz≠ 0), .
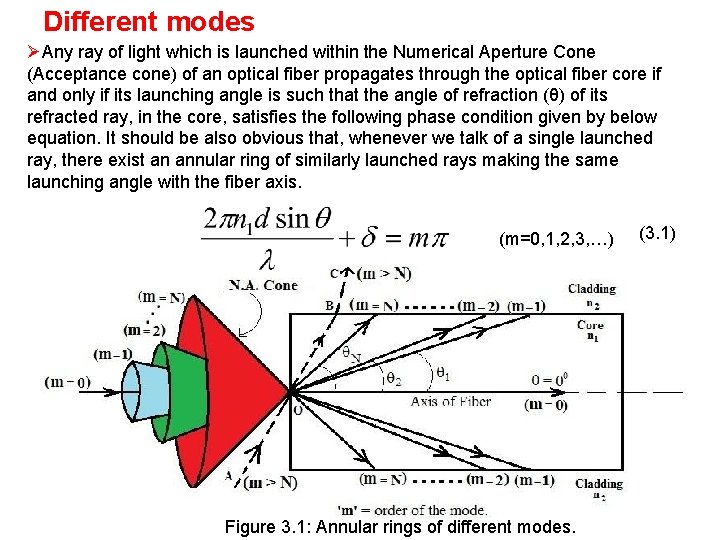
Different modes ØAny ray of light which is launched within the Numerical Aperture Cone (Acceptance cone) of an optical fiber propagates through the optical fiber core if and only if its launching angle is such that the angle of refraction (θ) of its refracted ray, in the core, satisfies the following phase condition given by below equation. It should be also obvious that, whenever we talk of a single launched ray, there exist an annular ring of similarly launched rays making the same launching angle with the fiber axis. (m=0, 1, 2, 3, …) Figure 3. 1: Annular rings of different modes. (3. 1)

ØThe number of different values of ‘m’ signifies the number of different possible launching angles which can successfully propagate in the optical fiber core. ØThere may be N possible modes of propagation for which the rays successfully travel along the fiber creating unique light intensity patterns around the axis of the core. ØThe ray that is launched along the axis of the fiber propagates without any phase condition requirement to be satisfied and corresponds to the first mode of propagation, also called as the zero order mode ( m=0) of propagation. ØAny ray that is launched outside this cone does not propagate along the fiber although it might correspond to a particular mode. This is shown in the figure above by the ray AO. ØThe optical fiber too is selective in accepting only those rays which satisfy the basic phase conditions and the other rays are rejected by the fiber although they may lie within the acceptance cone of the fiber. ØThus there are only a finite number of modes that are allowed in an optical fiber and the other modes are rejected. This leads to a further decrease in the light accepting efficiency of fiber.

ØTreating light a transverse electromagnetic wave, we find that when meridional rays propagate along the fiber, their electric and magnetic fields of all the rays superimpose to result in electric and magnetic field distribution which may be either transverse electric (TEx) or transverse magnetic (TMx) in nature. ØThe subscript ‘x’ denotes the definite number of maxima and minima in the resultant light intensity pattern. ØThe propagation of skew rays, on the other hand, results in a particularly special form of modes which are neither TE nor TM in nature and are called as Hybrid modes. ØWhen we refer to modal propagation in dielectric waveguides, we find that unlike metallic waveguides, there is a special set of modes that exists in a dielectric waveguide in addition to TE and TM modes. This set of modes is called as hybrid mode. The optical fiber is actually a cylindrical dielectric waveguide and so it can exhibit hybrid modes as well. Rigorous analysis shows that hybrid mode is in fact the lowest order mode that can propagate in an optical fiber. Since hybrid mode is the lowest order mode, it can be analytically shown that the mode of the ray that propagates in the fiber along the axis is hybrid in nature.
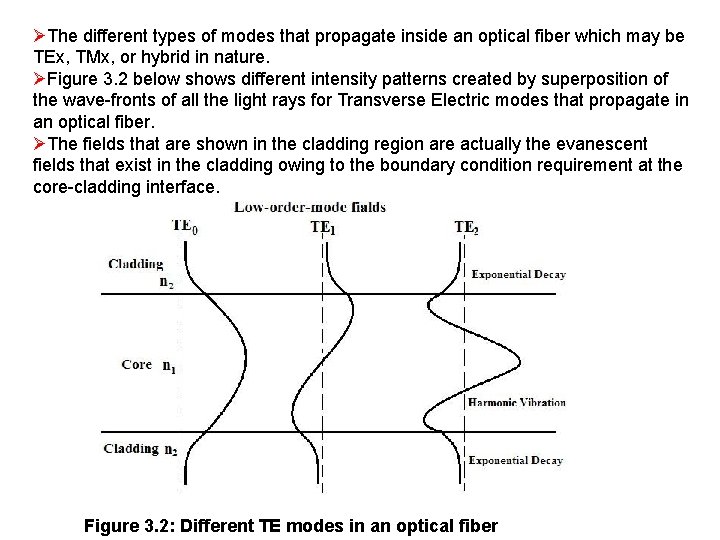
ØThe different types of modes that propagate inside an optical fiber which may be TEx, TMx, or hybrid in nature. ØFigure 3. 2 below shows different intensity patterns created by superposition of the wave-fronts of all the light rays for Transverse Electric modes that propagate in an optical fiber. ØThe fields that are shown in the cladding region are actually the evanescent fields that exist in the cladding owing to the boundary condition requirement at the core-cladding interface. Figure 3. 2: Different TE modes in an optical fiber

ØFor very low launching angles with respect to the axis of the fiber, the intensity pattern created is the one which is shown by TE 0 in the above figure. There exists a maximum intensity region around the axis of the core and as we move towards the periphery of the core the fields start to decay. These fields eventually decay down to negligibly low value in the cladding as shown in the figure. ØIf the launching angle is increased further, we get the intensity patterns as that shown for TE 1 and TE 2 in the above figure. ØThe subscript of TE in fact indicates the number of destructive interferences in the pattern where the field intensity crosses the zero level, or in other words, creates a optically dark area. ØSo, for TE 0 we have no dark area, for TE 1 we have one dark area at the axis, for TE 2 we have two dark areas and so on. ØThis situation is well obvious from the above figure which shows the number of times the field intensity pattern crosses the zero level corresponding to the subscript of TE. ØThis subscript is also termed as the index of the mode. As we further increase the launching angle with respect to the axis, more zeros are crossed and we get the higher indices of the mode. The above discussion is also true for TM mode as well and hence these modes are not referred to separately.
- Slides: 32