Optical Diffraction Parag Bhattacharya Department of Basic Sciences

Optical Diffraction Parag Bhattacharya Department of Basic Sciences School of Engineering and Technology Assam Don Bosco University

Concept of Diffraction

Optical Diffraction is a general characteristic of wave phenomena that occurs whenever a portion of a wavefront of light is obstructed in some way, leading to the deviation of light from rectilinear propagation. The Huygens-Fresnel Principle: Every unobstructed point on a wavefront, at a given instant, serves as a source of spherical secondary wavelets (with the same frequency as that of the primary wave). The amplitude of the optical field at any point beyond is the superposition of all these wavelets (considering their amplitudes and relative phases). In interference phenomena, the superposing beams originate from a discrete number of sources. In diffraction phenomena, the superposing beams originate from a continuous distribution of sources. The longer the wavelength compared to the aperture, the greater is the effect of diffraction.

Two broad categories of diffraction: Fresnel Diffraction Fraunhofer Diffraction Also called near-field diffraction. Also called far-field diffraction. Either the source or the screen or Both the source and the screen both are at finite distance from are at infinite distance from the diffraction aperture. Spherical wavefronts involved. Planar wavefronts only involved. The shape of the aperture is The projected pattern is recognisable with slight fringing comprised of intensity variations, around its periphery. and bears little or no resemblance to the aperture. As separation between the aperture and the screen increases, the size of the pattern increases, the image of the changes but its shape remains aperture becomes more the same. structured and fringes become more prominent.

Two broad categories of diffraction: Fresnel Diffraction Example: Fraunhofer Diffraction Example:

Fraunhofer Diffraction due to a single slit

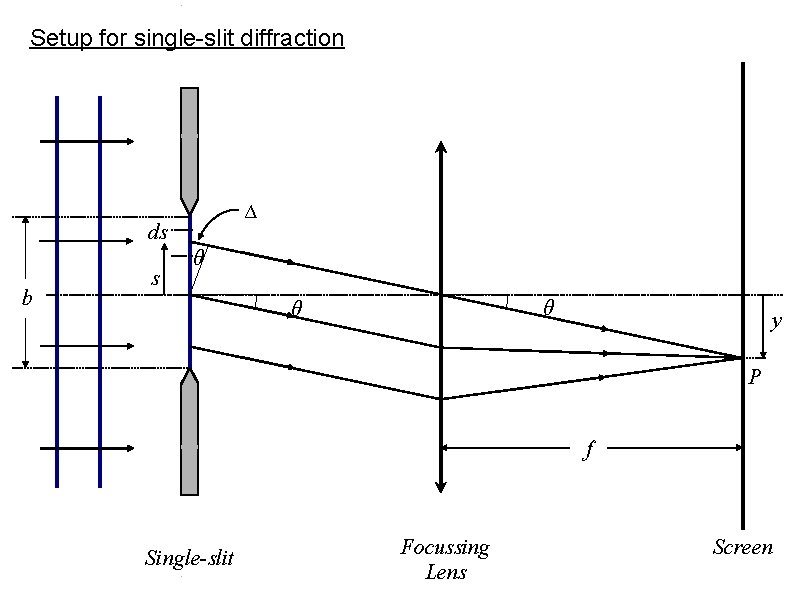
Setup for single-slit diffraction Δ ds b s θ θ θ y P f Single-slit Focussing Lens Screen

Strategy for applying the superposition principle Portion of wavefront at the slit acts as an extended source. Intensity at point P on the screen due to parallel rays from different portions of wavefront at the slit. We consider each infinitessimal portion ds of the wavefront at the slit as a source. Then we find the electric field due to ds. The resultant field is calculated by integrating over the entire slit width b.

Single-slit Diffraction: We define the field strength, i. e. , field per unit length E 0, to be uniform over the wavefront (since the wavefront is planar). Then the source field at length element ds is directly proportional to ds, i. e. , E 0 ds Thus, the field at P due to ds is (1) where r is the radial distance from a source For the wave from the centre of the slit, i. e. , s = 0, we set r = r 0 Then for a wave originating from a source ds at a height s, we have, r = r 0 + Δ. Therefore, (2)

Single-slit Diffraction: (2) Since Δ is very small compared to r 0, it can be ignored in the amplitude term. But cannot be ignored in the phase (Why? ? ? ) From the geometry, we have Δ = s sin θ Then (2) becomes: (3) Then the total field at P is: (4)

Single-slit Diffraction: (4) This integration gives: Substituting the limits of integration, we obtain, We define a new quantity: (5)

Single-slit Diffraction: (5) This gives: Therefore, we finally obtain, (6)

Single-slit Diffraction: Consider 2 parallel waves emitted from the slit: Δ b/2 θ θ 1 st wave from the centre 2 nd wave from either endpoint The separation between these 2 points on the wavefront portion is b/2. Say, these 2 waves make an angle θ with the optic axis. Then path difference between these waves is: And the corresponding phase difference is: Therefore, β can be interpreted as the phase difference (at point P) between 2 waves emitted from points on the slit separated by b/2.

Single-slit Diffraction: (6) The encircled quantity gives the amplitude of the resultant field at the point P. Thus, the amplitude at P: and Therefore the intensity I is:

Single-slit Diffraction: Hence, (7) where, We define a new function called the sinc function as: Then (7) becomes: (8) In (8), I 0 is a constant. So the intensity variation due to Fraunhofer diffraction follows the square of the sinc function. Hence, we now briefly have a look at the sinc function.

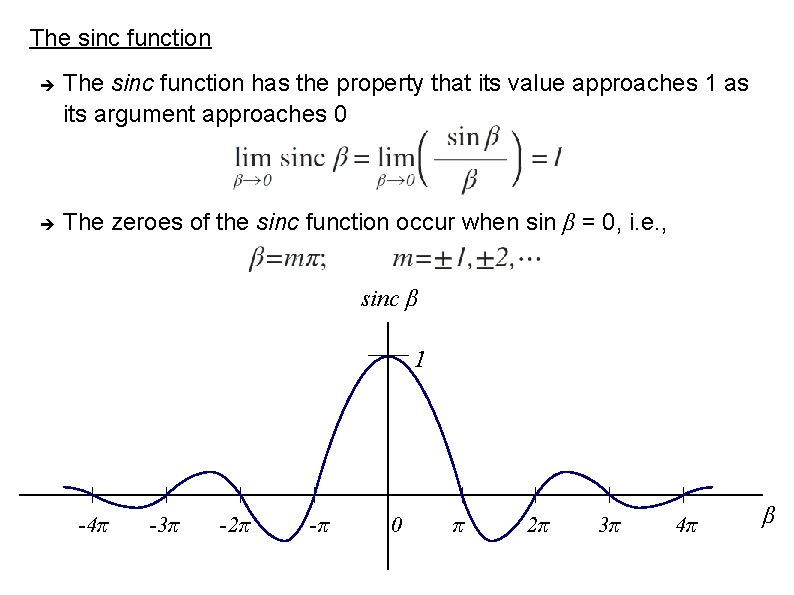
The sinc function has the property that its value approaches 1 as its argument approaches 0 The zeroes of the sinc function occur when sin β = 0, i. e. , sinc β 1 -4π -3π -2π -π 0 π 2π 3π 4π β

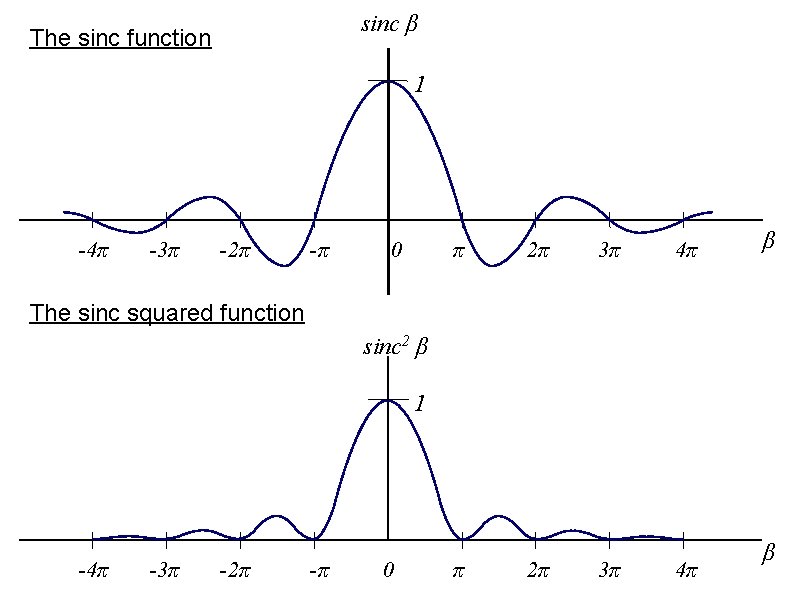
sinc β The sinc function 1 -4π -3π -2π -π 0 π 2π 3π 4π β The sinc squared function sinc 2 β 1 -4π -3π -2π -π 0 π 2π 3π 4π β

Intensity distribution The intensity varies as: The maximum value of the intensity is I 0. This occurs at β = 0. This position is known as the central maximum. The dark regions occur at the zeros of the sinc function. These occur at β = mπ. These positions are known as points of minima. (9) From the geometry of the set-up, y is small compared to f. Hence θ is also small. Thus, using the small-angle approximation:

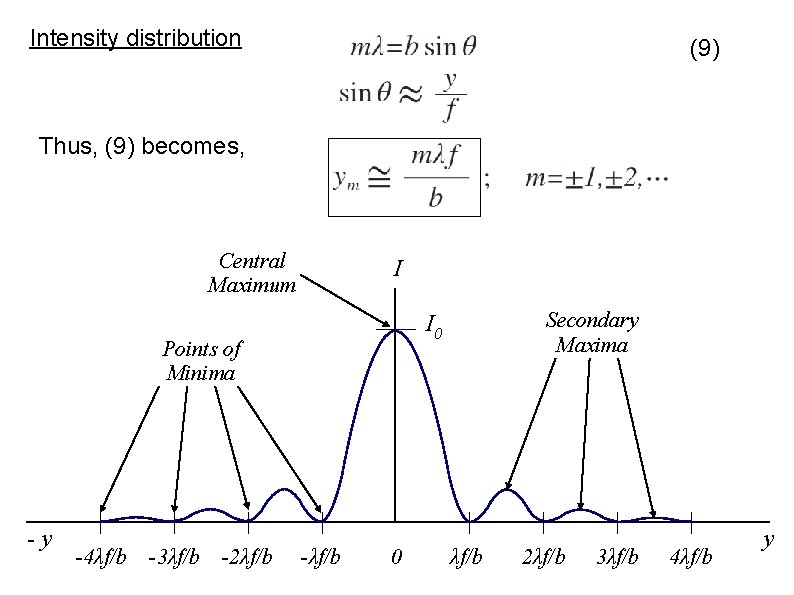
Intensity distribution (9) Thus, (9) becomes, Central Maximum I Points of Minima -y -4λf/b -3λf/b -2λf/b Secondary Maxima I 0 -λf/b 0 λf/b 2λf/b 3λf/b 4λf/b y

Fraunhofer Diffraction due to a plane transmission grating

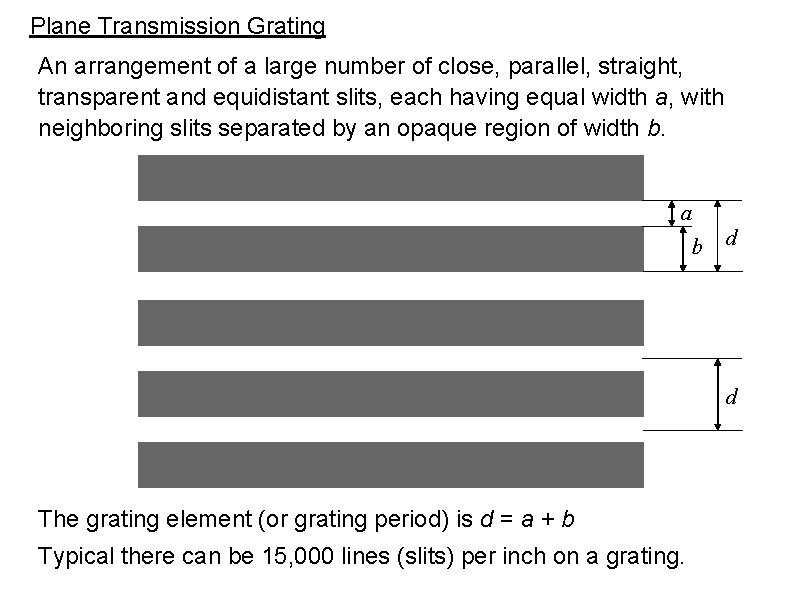
Plane Transmission Grating An arrangement of a large number of close, parallel, straight, transparent and equidistant slits, each having equal width a, with neighboring slits separated by an opaque region of width b. a b d d The grating element (or grating period) is d = a + b Typical there can be 15, 000 lines (slits) per inch on a grating.

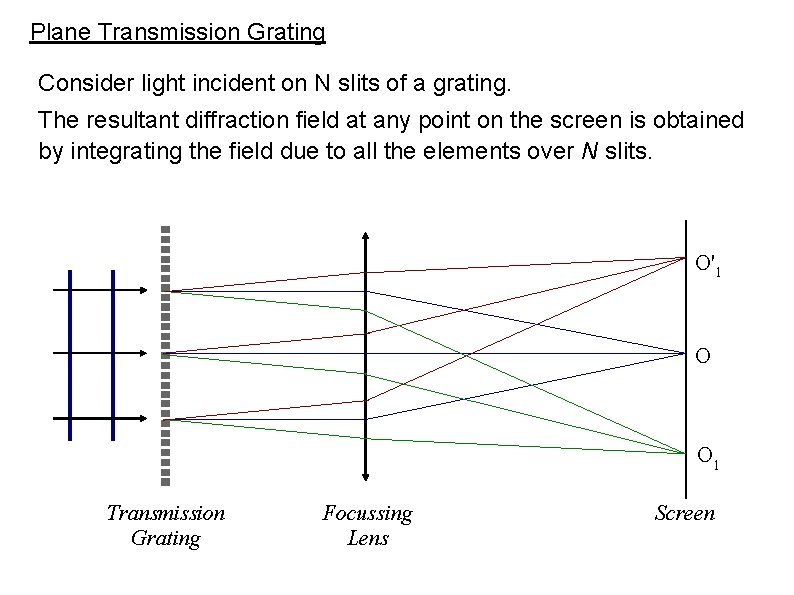
Plane Transmission Grating Consider light incident on N slits of a grating. The resultant diffraction field at any point on the screen is obtained by integrating the field due to all the elements over N slits. O'1 O O 1 Transmission Grating Focussing Lens Screen

Plane Transmission Grating The integration over N slits gives the resultant field at a point P on the screen as: (1) (Derivation not necessary) The quantity in square brackets is the amplitude of the resultant field. Here, and (2) where, d: grating element and a: slit size Then the intensity variation on the screen is: (3) Diffraction Term Interference Term

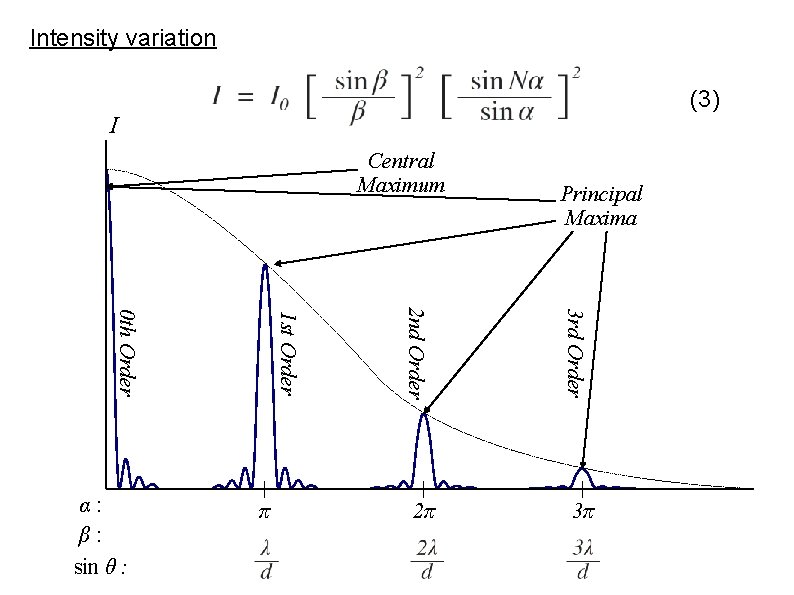
Intensity variation (3) I Central Maximum 2π 3 rd Order π 2 nd Order 1 st Order 0 th Order α: β: sin θ : Principal Maxima 3π

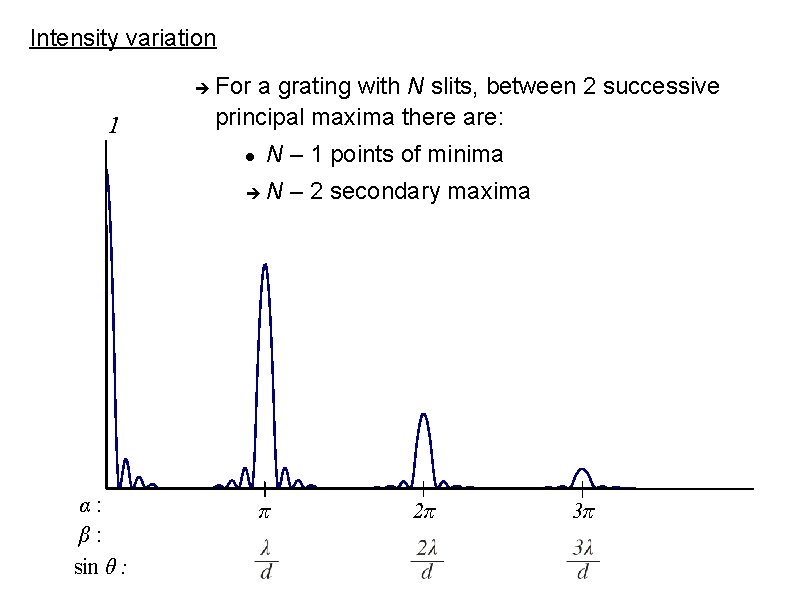
Intensity variation 1 α: β: sin θ : For a grating with N slits, between 2 successive principal maxima there are: N – 1 points of minima N – 2 secondary maxima π 2π 3π

Positions for the principal maxima (3) Diffraction Term Interference Term where, The positions of all the minima and principal maxima are governed by the interference term. These positions occur when we have (4) principal maxima occur for secondary minima occur for p = all other integer values (5)

Positions for the principal maxima (4) principal maxima occur for As per (5), for principal maxima, we must have Thus, the condition for principal maxima becomes: (5)

Positions for the principal maxima Thus, the condition for principal maxima becomes: Therefore, (6) Equation (6) is known as the diffraction grating equation. The quantity m is called the order of the diffraction.

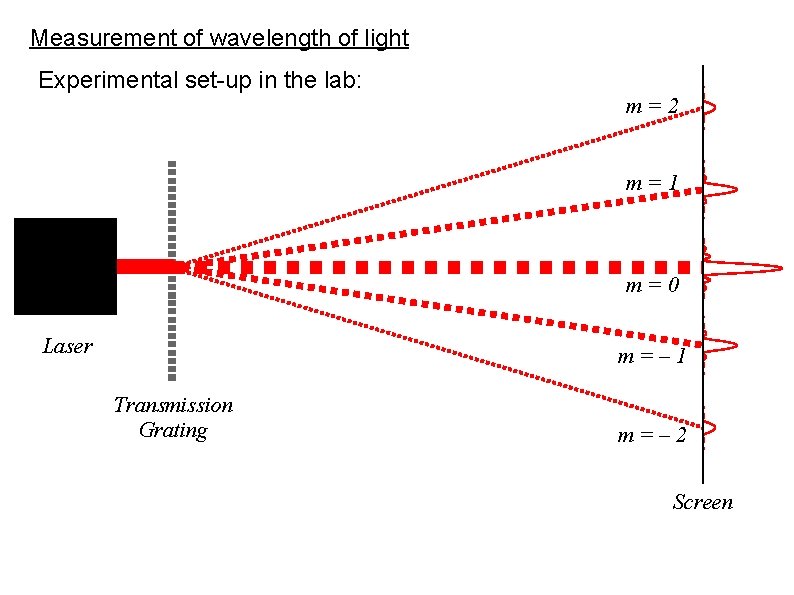
Measurement of wavelength of light Experimental set-up in the lab: m=2 m=1 m=0 Laser m=– 1 Transmission Grating m=– 2 Screen

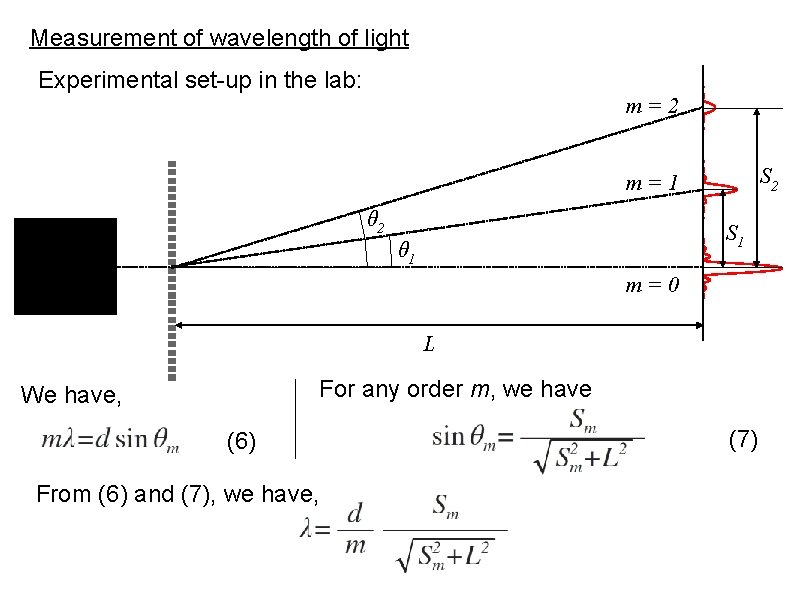
Measurement of wavelength of light Experimental set-up in the lab: m=2 S 2 m=1 θ 2 S 1 θ 1 m=0 L For any order m, we have We have, (6) From (6) and (7), we have, (7)

Fresnel Zone Plates

A zone plate is a device used to focus light. A zone plate uses diffraction in order to focus light (unlike lenses and spherical mirrors that use reflection or refraction). Based on the analysis by Augustin Jean-Fresnel. A zone plate consists of a set of radially symmetric rings, known as Fresnel zones, which alternate between opaque and transparent. Light hitting the zone plate will diffract around the opaque zones. The zones can be spaced so that the diffracted light constructively interferes at the desired focus, creating an image there.

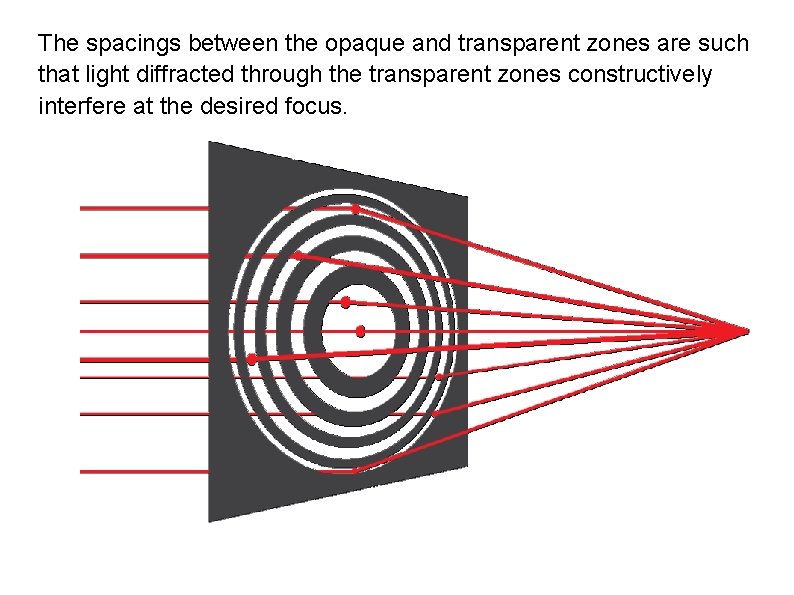
The spacings between the opaque and transparent zones are such that light diffracted through the transparent zones constructively interfere at the desired focus.

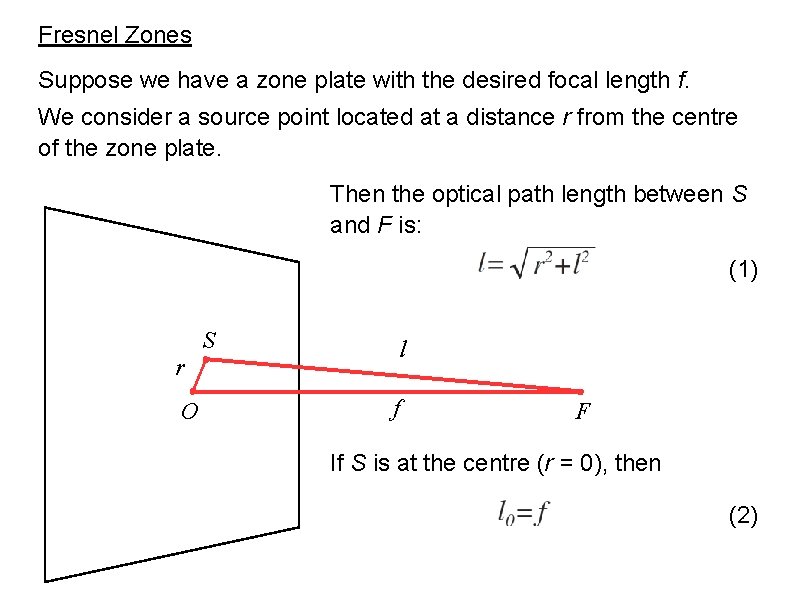
Fresnel Zones Suppose we have a zone plate with the desired focal length f. We consider a source point located at a distance r from the centre of the zone plate. Then the optical path length between S and F is: (1) S r O l f F If S is at the centre (r = 0), then (2)

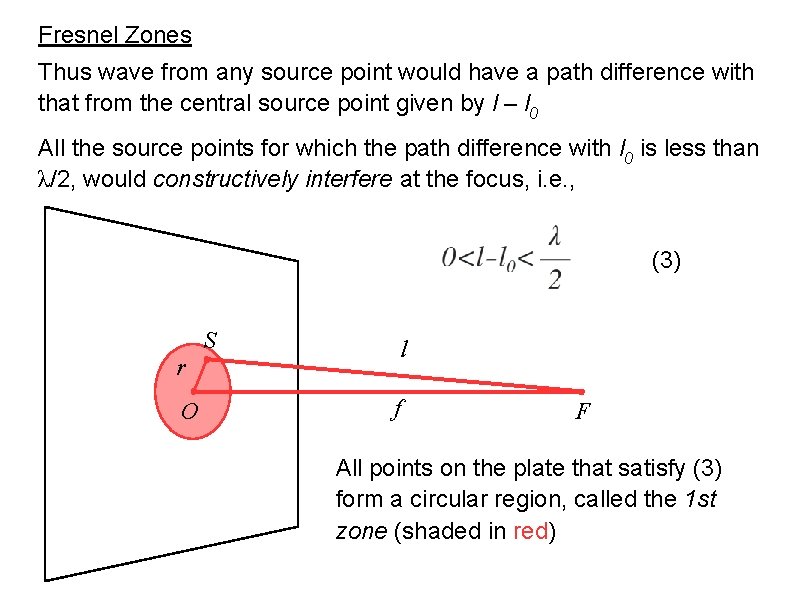
Fresnel Zones Thus wave from any source point would have a path difference with that from the central source point given by l – l 0 All the source points for which the path difference with l 0 is less than λ/2, would constructively interfere at the focus, i. e. , (3) S r O l f F All points on the plate that satisfy (3) form a circular region, called the 1 st zone (shaded in red)

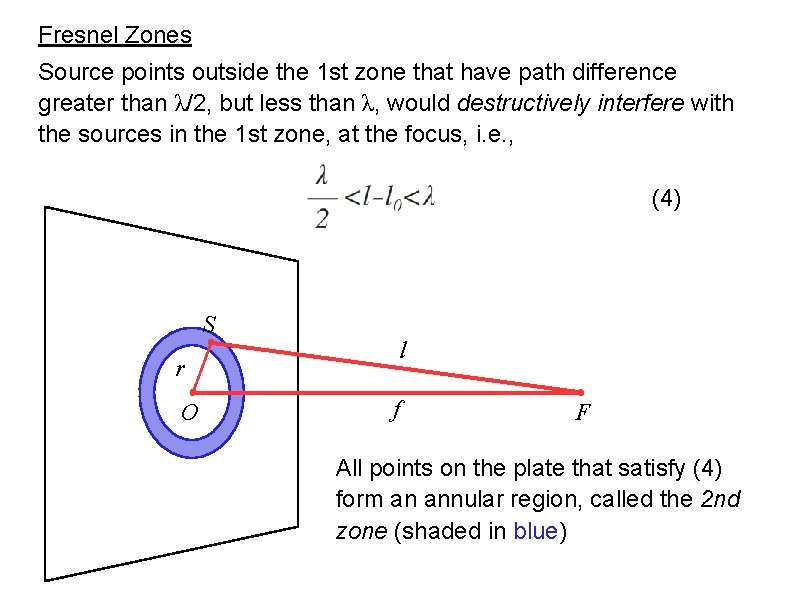
Fresnel Zones Source points outside the 1 st zone that have path difference greater than λ/2, but less than λ, would destructively interfere with the sources in the 1 st zone, at the focus, i. e. , (4) S r O l f F All points on the plate that satisfy (4) form an annular region, called the 2 nd zone (shaded in blue)

Fresnel Zones Thus, we have: 1 st Zone: 2 nd Zone: Proceeding in this manner, the nth zone may be defined as the collection of those points on the plate whose path difference satisfy the following relation: (5) where, n is a positive integer such that 1 ≤ n ≤ N, and N is the total number of zones in the plate. Point sources from odd zones (n = 1, 3, 5, . . . ) -> interfere constructively with the 1 st zone Point sources from even zones (n = 2, 4, 6, . . . ) -> interfere destructively with the

Fresnel Zones Point sources from odd zones (n = 1, 3, 5, . . . ) -> interfere constructively with the 1 st zone Point sources from even zones (n = 2, 4, 6, . . . ) -> interfere destructively with the 1 st zone In order to maximise the constructive interference at the focus, the zone plate is constructed as: Odd-numbered zones are made transparent (to enable light to pass through) Even-numbered zones are made opaque (to block the light) Note: The choice of the 1 st zone as the reference is arbitrary. If the zone plates are inverted, i. e. , opaque odd zones and transparent even zones, the effect would be the same. (Can you figure out why? )

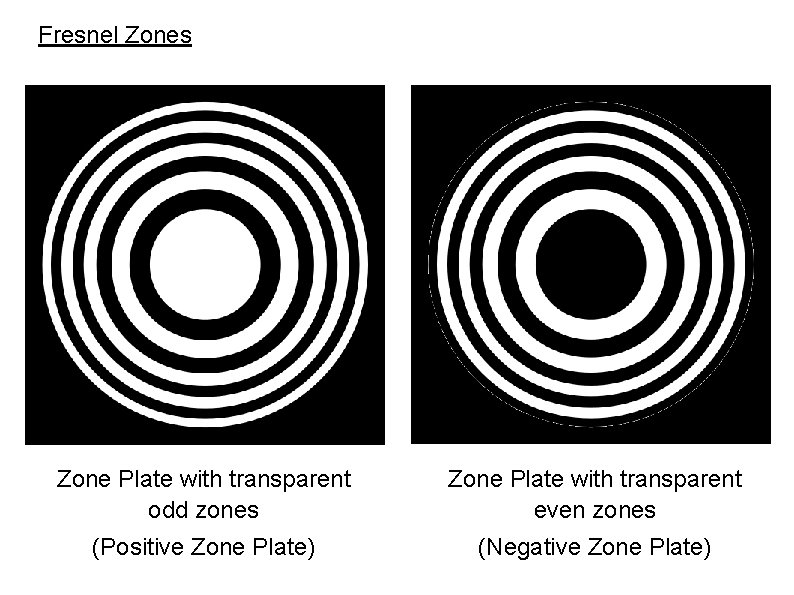
Fresnel Zones Zone Plate with transparent odd zones Zone Plate with transparent even zones (Positive Zone Plate) (Negative Zone Plate)

Determination of the zone radii (1) (2) The outer zone boundary for the nth zone is given as: (6) Using (1) and (2) in (6), we obtain, Solving for rn, we obtain the zone radius for the nth zone as: (7)

Determination of the zone radii (7) Generally, Hence, Thus, the 2 nd term in (7) is negligible compared to the 1 st term. Therefore, in the 1 st approximation, (8) shows that Thus,

Home-work Q 1. Arrive at the expression for the surface area of the nth zone. Q 2. Show that, in the 1 st approximation, the area of any zone is constant.

References: 1) 2) 3) “Optics”, 4 th Ed. , Eugene Hecht & A. R. Ganesan, Pearson “Introduction to Optics”, 3 rd Ed. , Frank L. Pedrotti, Leno M. Pedrotti & Leno S. Pedrotti, Pearson “Physics for Engineers and Technologists”, Samrat Dey, EBH Publishers

Thank You! Assam Don Bosco University