Optical Design of Waveguides for Operation in the

Optical Design of Waveguides for Operation in the Visible and Infrared Mustafa Yorulmaz Bilkent University, Physics Department May 25, 2007 Bilkent University, Physics Department 1

Outline n n n n Waveguide theory Simulation Methodology State-of-the-art of rib-waveguides Our rib-waveguide designs State-of-the art of slot-waveguides Our slot-waveguide design Achievements May 25, 2007 Bilkent University, Physics Department 2

Planar mirror waveguides Wave-fronts and raypaths The picture shows the wave-fronts in addition to the ray model. In order to have constructive interference, the twice reflected wave must be in phase with the incident wave: The angle of inclination is discrete, only a limited number of angles are permitted for constructive interference. May 25, 2007 Bilkent University, Physics Department 3

The number of modes of a waveguide is limited It is derived that the angle of inclination is discrete: since The total number of modes is M, which is a function of waveguide thickness and the wavelength. If 2 d/λ<1 no modes available thus λmax=2 d or fmin=c/2 d (cut-off frequency). If M=1, i. e. 1<2 d/λ<2 then the wave guide is called single-mode Example: If d=0. 5μ, the cut-off wavelength is 1μ. The waveguide is singlemode for wavelengths down to 0. 5μ, and multi-mode for lower wavelength operations. May 25, 2007 Bilkent University, Physics Department 4

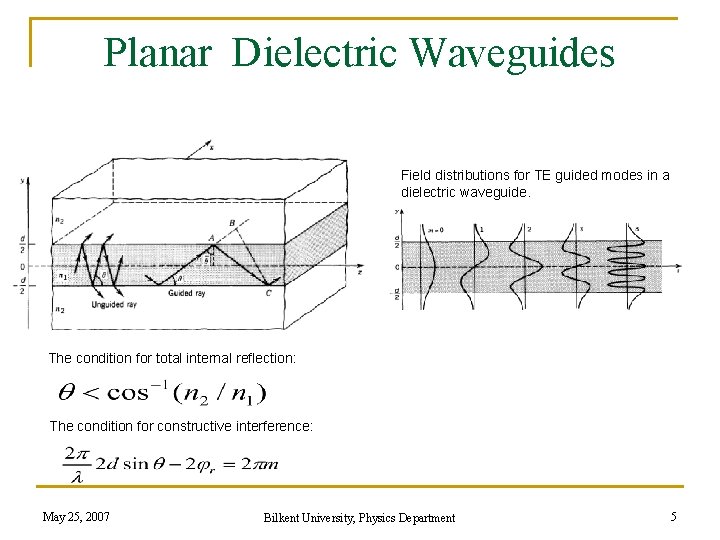
Planar Dielectric Waveguides Field distributions for TE guided modes in a dielectric waveguide. The condition for total internal reflection: The condition for constructive interference: May 25, 2007 Bilkent University, Physics Department 5

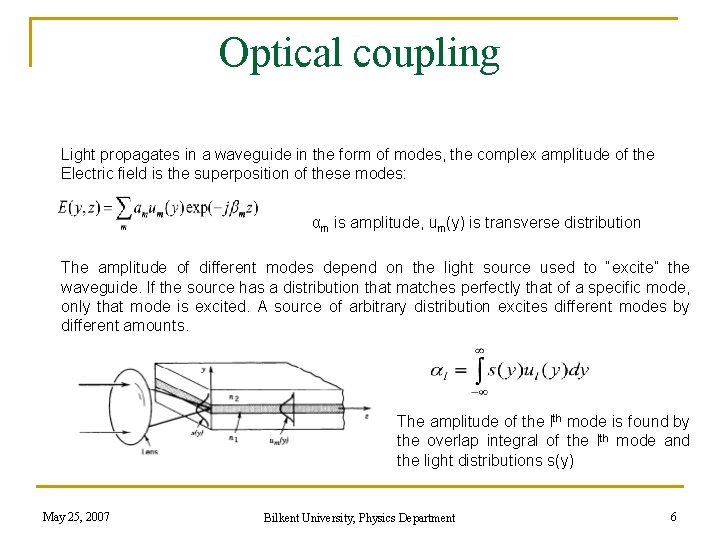
Optical coupling Light propagates in a waveguide in the form of modes, the complex amplitude of the Electric field is the superposition of these modes: αm is amplitude, um(y) is transverse distribution The amplitude of different modes depend on the light source used to “excite” the waveguide. If the source has a distribution that matches perfectly that of a specific mode, only that mode is excited. A source of arbitrary distribution excites different modes by different amounts. The amplitude of the lth mode is found by the overlap integral of the lth mode and the light distributions s(y) May 25, 2007 Bilkent University, Physics Department 6

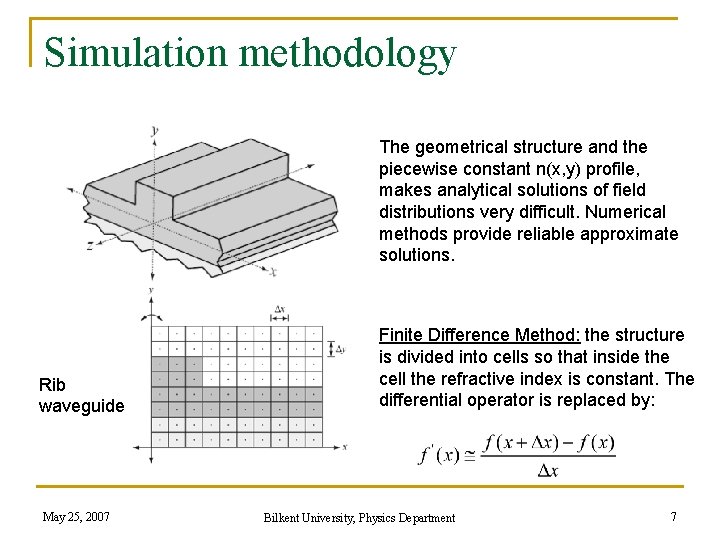
Simulation methodology The geometrical structure and the piecewise constant n(x, y) profile, makes analytical solutions of field distributions very difficult. Numerical methods provide reliable approximate solutions. Rib waveguide May 25, 2007 Finite Difference Method: the structure is divided into cells so that inside the cell the refractive index is constant. The differential operator is replaced by: Bilkent University, Physics Department 7

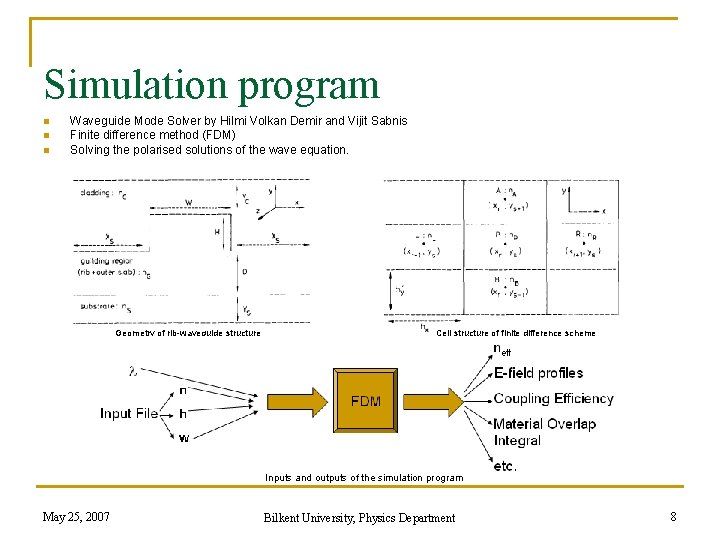
Simulation program n n n Waveguide Mode Solver by Hilmi Volkan Demir and Vijit Sabnis Finite difference method (FDM) Solving the polarised solutions of the wave equation. Geometry of rib-waveguide structure Cell structure of finite difference scheme Inputs and outputs of the simulation program May 25, 2007 Bilkent University, Physics Department 8

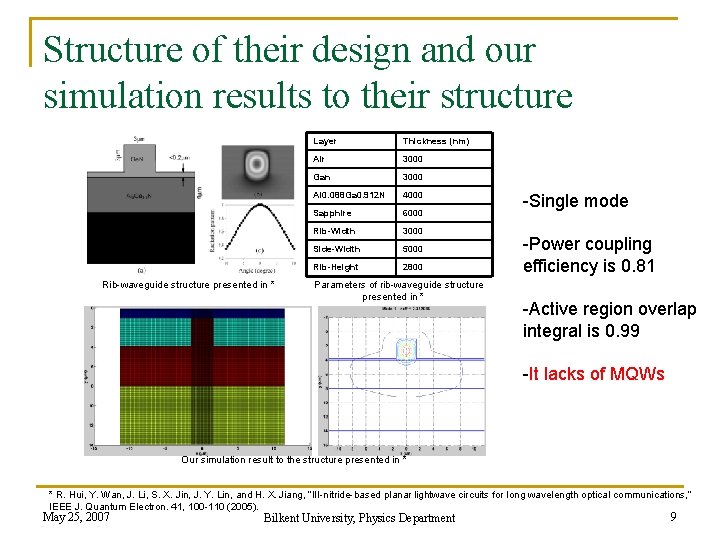
Structure of their design and our simulation results to their structure Rib-waveguide structure presented in * Layer Thickness (nm) Air 3000 Gan 3000 Al 0. 088 Ga 0. 912 N 4000 Sapphire 6000 Rib-Width 3000 Side-Width 5000 Rib-Height 2800 Parameters of rib-waveguide structure presented in * -Single mode -Power coupling efficiency is 0. 81 -Active region overlap integral is 0. 99 -It lacks of MQWs Our simulation result to the structure presented in * * R. Hui, Y. Wan, J. Li, S. X. Jin, J. Y. Lin, and H. X. Jiang, “III-nitride-based planar lightwave circuits for long wavelength optical communications, ” IEEE J. Quantum Electron. 41, 100 -110 (2005). May 25, 2007 Bilkent University, Physics Department 9

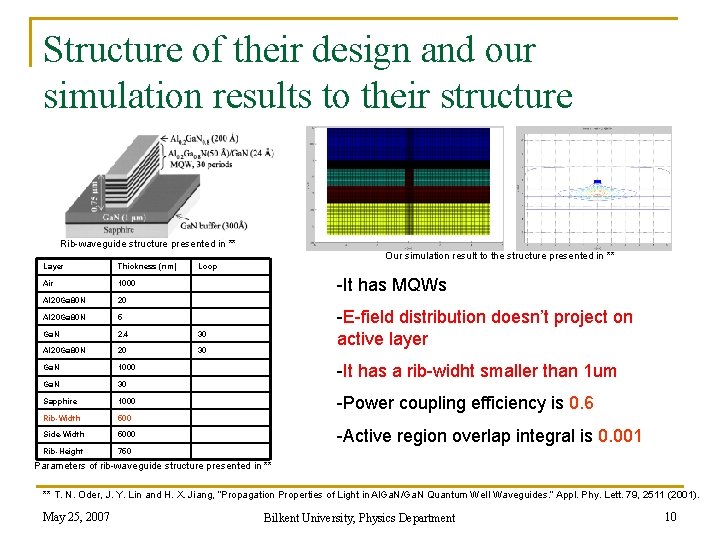
Structure of their design and our simulation results to their structure Rib-waveguide structure presented in ** Our simulation result to the structure presented in ** Layer Thickness (nm) Loop Air 1000 Al 20 Ga 80 N 20 Al 20 Ga 80 N 5 Ga. N 2. 4 30 Al 20 Ga 80 N 20 30 Ga. N 1000 Ga. N 30 Sapphire 1000 Rib-Width 500 Side-Width 5000 Rib-Height 750 -It has MQWs -E-field distribution doesn’t project on active layer -It has a rib-widht smaller than 1 um -Power coupling efficiency is 0. 6 -Active region overlap integral is 0. 001 Parameters of rib-waveguide structure presented in ** ** T. N. Oder, J. Y. Lin and H. X. Jiang, “Propagation Properties of Light in Al. Ga. N/Ga. N Quantum Well Waveguides. ” Appl. Phy. Lett. 79, 2511 (2001). May 25, 2007 Bilkent University, Physics Department 10

Challenges for Design n n n Rib-width > 1 mm for fabrication Single mode Having MQWs Circular mode profile Material overlap integral Coupling Efficiency May 25, 2007 Bilkent University, Physics Department 11

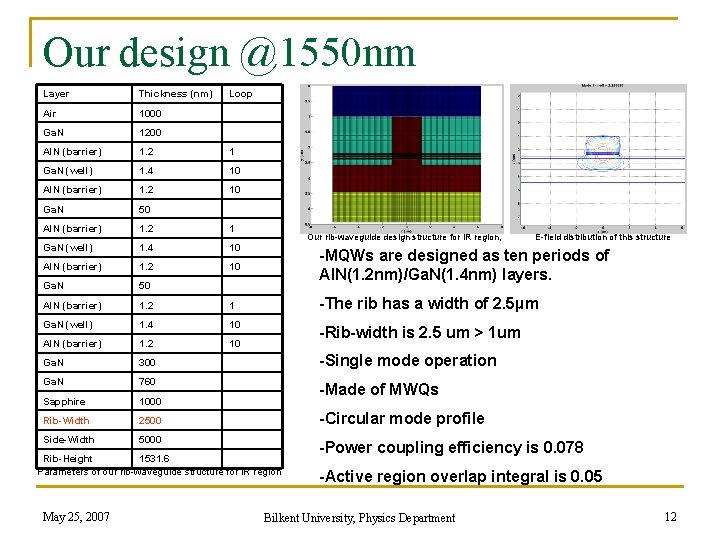
Our design @1550 nm Layer Thickness (nm) Loop Air 1000 Ga. N 1200 Al. N (barrier) 1. 2 1 Ga. N (well) 1. 4 10 Al. N (barrier) 1. 2 10 Ga. N 50 -MQWs are designed as ten periods of Al. N(1. 2 nm)/Ga. N(1. 4 nm) layers. Al. N (barrier) 1. 2 1 -The rib has a width of 2. 5µm Ga. N (well) 1. 4 10 Al. N (barrier) 1. 2 10 Ga. N 300 Ga. N 760 Sapphire 1000 Rib-Width 2500 Side-Width 5000 Our rib-waveguide design structure for IR region, -Rib-width is 2. 5 um > 1 um -Single mode operation -Made of MWQs -Circular mode profile Rib-Height 1531. 6 Parameters of our rib-waveguide structure for IR region May 25, 2007 E-field distribution of this structure -Power coupling efficiency is 0. 078 -Active region overlap integral is 0. 05 Bilkent University, Physics Department 12

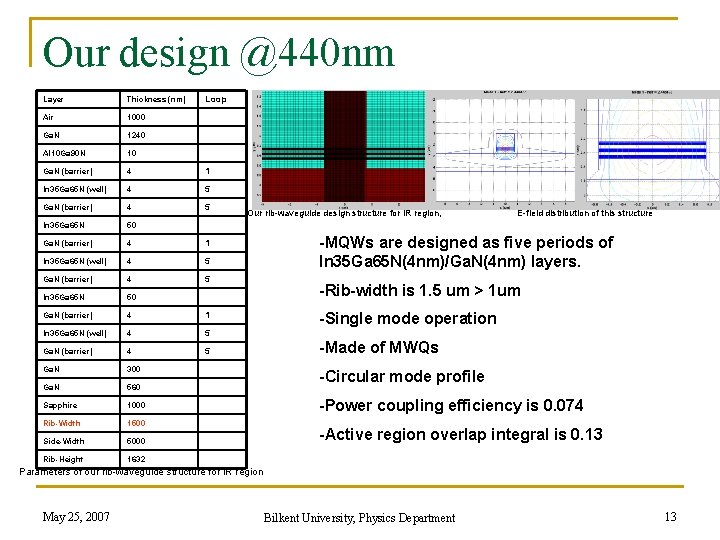
Our design @440 nm Layer Thickness (nm) Air 1000 Ga. N 1240 Al 10 Ga 90 N 10 Ga. N (barrier) 4 1 In 35 Ga 65 N (well) 4 5 Ga. N (barrier) 4 5 In 35 Ga 65 N 50 Ga. N (barrier) 4 1 In 35 Ga 65 N (well) 4 5 Ga. N (barrier) 4 5 Ga. N 300 Ga. N 560 Sapphire 1000 Rib-Width 1500 Side-Width 5000 Rib-Height 1632 Loop Our rib-waveguide design structure for IR region, E-field distribution of this structure -MQWs are designed as five periods of In 35 Ga 65 N(4 nm)/Ga. N(4 nm) layers. -Rib-width is 1. 5 um > 1 um -Single mode operation -Made of MWQs -Circular mode profile -Power coupling efficiency is 0. 074 -Active region overlap integral is 0. 13 Parameters of our rib-waveguide structure for IR region May 25, 2007 Bilkent University, Physics Department 13

Achievements with our rib-waveguide designs n n n Having MQWs Satisfying single mode operation Rib width > 1 mm (@440 nm and @1550 nm) Power coupling ~ 0. 7 -0. 8 (@440 nm and @1550 nm) Material Overlap > 0. 1 (@440 nm) May 25, 2007 Bilkent University, Physics Department 14

New type of waveguide design: Slot-waveguide n n Different way for confining and enhancing light: Guiding light in lowindex materials According to the Maxwell’s laws that the electric field must undergo a large discontinuity with much higher amplitude in the low index side to satisfy the continuity of the normal component of electric flux density for a high-index-contrast interface. So that, this discontinuity is used to strongly enhance and confine light in a nanometer-wide region of low index material Parameters • nc • ns • nh • ws • h Geometry of slot-waveguide structure presented *** V. Almeida, Q. Xu, C. Barrios, and M. Lipson, “Guiding and confining light in void nanostructure, ” Opt. Lett. 29, 1209 (2004). [ISI]. May 25, 2007 Bilkent University, Physics Department 15

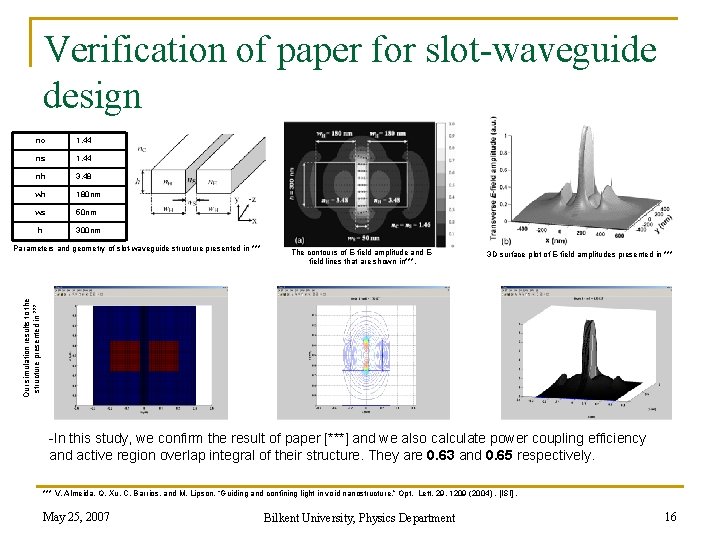
Verification of paper for slot-waveguide design nc 1. 44 ns 1. 44 nh 3. 48 wh 180 nm ws 50 nm h 300 nm The contours of E-field amplitude and Efield lines that are shown in***. 3 D surface plot of E-field amplitudes presented in *** Our simulation results to the structure presented in *** Parameters and geometry of slot-waveguide structure presented in *** -In this study, we confirm the result of paper [***] and we also calculate power coupling efficiency and active region overlap integral of their structure. They are 0. 63 and 0. 65 respectively. *** V. Almeida, Q. Xu, C. Barrios, and M. Lipson, “Guiding and confining light in void nanostructure, ” Opt. Lett. 29, 1209 (2004). [ISI]. May 25, 2007 Bilkent University, Physics Department 16

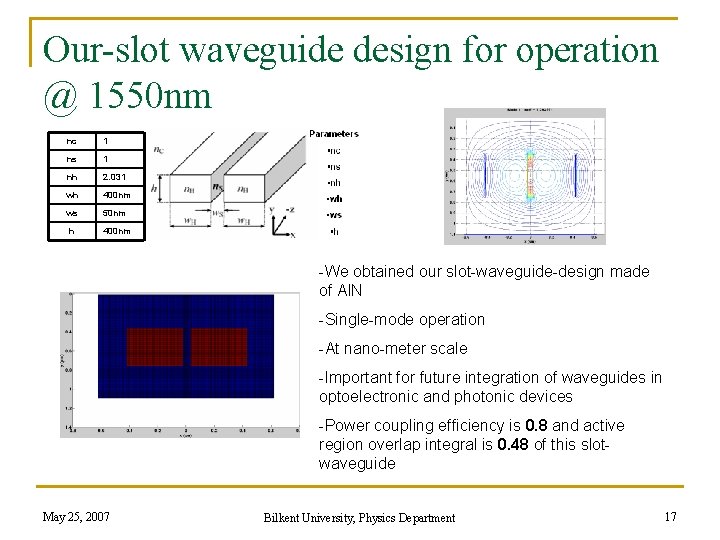
Our-slot waveguide design for operation @ 1550 nm nc 1 ns 1 nh 2. 031 wh 400 nm ws 50 nm h 400 nm -We obtained our slot-waveguide-design made of Al. N -Single-mode operation -At nano-meter scale -Important for future integration of waveguides in optoelectronic and photonic devices -Power coupling efficiency is 0. 8 and active region overlap integral is 0. 48 of this slotwaveguide May 25, 2007 Bilkent University, Physics Department 17

Thanks. . Questions? May 25, 2007 Bilkent University, Physics Department 18