Operators and Expectation Values Operators A function is

Operators and Expectation Values Operators • A function is something that turns numbers into numbers • An operator is something that turns functions into functions – Example: The derivative operator • In quantum mechanics, x cannot be the position of a particle – Particles don’t have a definite position • Instead, think of x as something you multiply a wave function by to get a new wave function – x is an operator, sometimes written as xop or X • There are lots of other operators as well, like momentum

Expectation Values • Suppose we know the wave function (x) and we measure x. What answer will we get? – We only know probability of getting different values – Let’s find the average value you get • Recall | (x)|2 tells you the probability density that it is at x – We want an expectation value • It is denoted by x • For any operator, we can similarly get an average measurement

Sample Problem A particle is in the ground state of a harmonic oscillator. What is the expectation value of the operators x, x 2, and p? Note: x 2 More on this later Note: Always use normalized wave functions for expectation values!

The Hamiltonian Operator • In classical mechanics, the Hamiltonian is the formula for energy in terms of the position x and momentum p • In quantum, the formula is the same, but x and p are reinterpreted as operators • Schrodinger’s equations rewritten with the Hamiltonian: • The expectation value of the Hamiltonian is the average value you would get if you measure the energy Advanced Physics: • The Hamiltonian becomes much more complicated – More dimensions, multiple particles, special relativity • But Schrodinger’s equation in terms of H remain the same

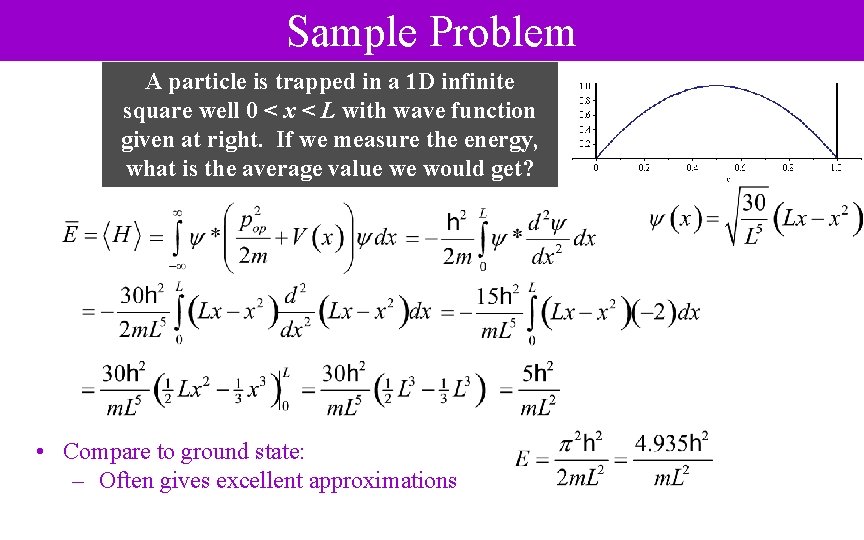
Sample Problem A particle is trapped in a 1 D infinite square well 0 < x < L with wave function given at right. If we measure the energy, what is the average value we would get? • Compare to ground state: – Often gives excellent approximations

Tricks for Finding Expectation Values • We often want expectation values of x or x 2 or p 2 • If our wave function is real, p is trivial • To find p 2, we will use integration by parts

Uncertainty • Recall: x 2. Why? • The difference between these is a measure of how spread out the wave function is • Define the uncertainty in x: We can similarly define the uncertainty in any operator: Heisenberg Uncertainty Principle

Sample Problem A particle is in the ground state of a harmonic oscillator. Find the uncertainty in x and p, and check that it obeys uncertainty principle • Much of the work was done five slides ago • We even found p , but since is real, it is trivial anyway • Now work out p 2: • Now get the uncertainties