Operations Research Modeling Toolset Queueing Theory Simulation Inventory

Operations Research Modeling Toolset Queueing Theory Simulation Inventory Theory Forecasting Game Theory Markov Chains Markov Decision Processes Decision Analysis Dynamic Programming PERT/ CPM Network Programming Linear Programming Stochastic Programming Nonlinear Programming Integer Programming 1

Network Problems • Linear programming has a wide variety of applications • Network problems – Special types of linear programs – Particular structure involving networks • Ultimately, a network problem can be represented as a linear programming model • However the resulting A matrix is very sparse, and involves only zeroes and ones • This structure of the A matrix led to the development of specialized algorithms to solve network problems 2

Types of Network Problems • Shortest Path Special case: Project Management with PERT/CPM • Minimum Spanning Tree • Maximum Flow/Minimum Cut • Minimum Cost Flow Special case: Transportation and Assignment Problems • Set Covering/Partitioning • Traveling Salesperson • Facility Location and many more 3

The Transportation Problem 4

The Transportation Problem • The problem of finding the minimum-cost distribution of a given commodity from a group of supply centers (sources) i=1, …, m to a group of receiving centers (destinations) j=1, …, n • Each source has a certain supply (si) • Each destination has a certain demand (dj) • The cost of shipping from a source to a destination is directly proportional to the number of units shipped 5

Simple Network Representation 1 Supply s 2 2 … Supply s 1 Destinations 1 Demand d 1 2 Demand d 2 … Sources xij Supply sm n m Demand dn Costs cij 6

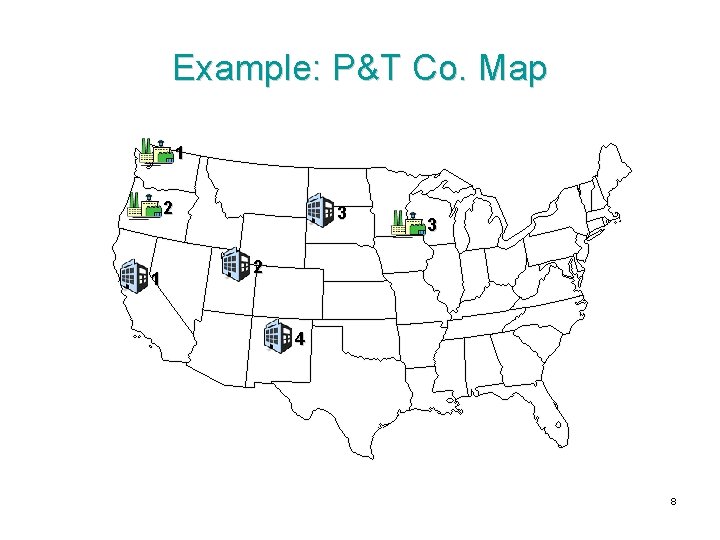
Example: P&T Co. • Produces canned peas at three canneries Bellingham, WA, Eugene, OR, and Albert Lea, MN • Ships by truck to four warehouses Sacramento, CA, Salt Lake City, UT, Rapid City, SD, and Albuquerque, NM • Estimates of shipping costs, production capacities and demands for the upcoming season is given • The management needs to make a plan on the least costly shipments to meet demand 7

Example: P&T Co. Map 1 2 1 3 3 2 4 8

Example: P&T Co. Data Warehouse Supply Cannery 1 2 3 4 1 $ 464 $ 513 $ 654 $ 867 75 2 $ 352 $ 216 $ 690 $ 791 125 3 $ 995 $ 682 $ 388 $ 685 100 Demand 80 65 70 85 (Truckloads) Shipping cost per truckload 9

Example: P&T Co. • Network representation 10

Example: P&T Co. • Linear programming formulation Let xij denote… Minimize subject to 11

General LP Formulation for Transportation Problems 12

Feasible Solutions • A transportation problem will have feasible solutions if and only if • How to deal with cases when the equation doesn’t hold? 13

Integer Solutions Property: Unimodularity • Unimodularity relates to the properties of the A matrix (determinants of the submatrices, beyond scope) • Transportation problems are unimodular, so we get the integers solutions property: For transportation problems, when every si and dj have an integer value, every BFS is integer valued. • Most network problems also have this property. 14

Transportation Simplex Method • Since any transportation problem can be formulated as an LP, we can use the simplex method to find an optimal solution • Because of the special structure of a transportation LP, the iterations of the simplex method have a very special form • The transportation simplex method is nothing but the original simplex method, but it streamlines the iterations given this special form 15

Transportation Simplex Method Initialization (Find initial CPF solution) Is the current CPF solution optimal? Yes Stop No Move to a better adjacent CPF solution 16

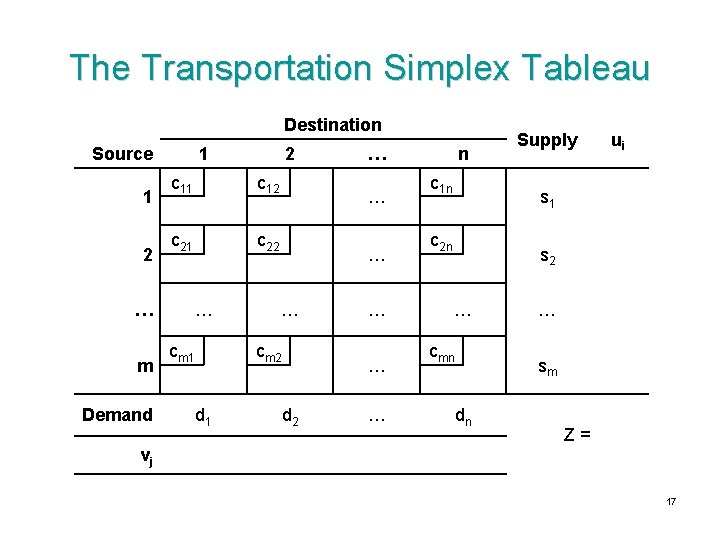
The Transportation Simplex Tableau Destination Source 1 2 … m Demand 1 2 c 11 c 12 c 21 c 22 … cm 1 … … … cm 2 d 1 … … … d 2 … n c 1 n Supply ui s 1 c 2 n s 2 … cmn … sm dn Z= vj 17

Prototype Problem • Holiday shipments of i. Pods to distribution centers • Production at 3 facilities, – A, supply 200 k – B, supply 350 k – C, supply 150 k • Distribute to 4 centers, – – N, demand 100 k S, demand 140 k E, demand 300 k W, demand 250 k • Total demand vs. total supply 18

Prototype Problem Destination Source A B C Dummy Demand N S E W 16 13 22 17 14 13 19 15 9 20 23 10 0 0 100 140 300 Supply ui 200 350 150 90 250 Z= vj 19

Finding an Initial BFS • The transportation simplex starts with an initial basic feasible solution (as does regular simplex) • There alternative ways to find an initial BFS, most common are – The Northwest corner rule – Vogel’s method – Russell’s method (beyond scope) 20

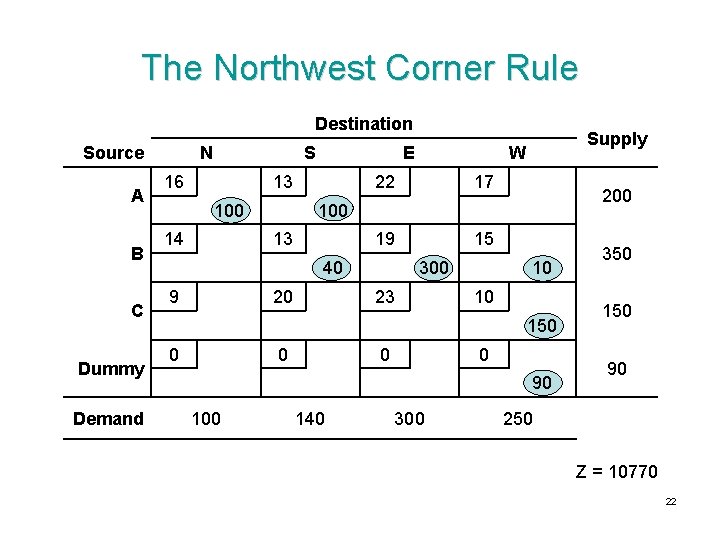
The Northwest Corner Rule • Begin by selecting x 11, let x 11 = min{ s 1, d 1 } • Thereafter, if xij was the last basic variable selected, – Select xi(j+1) if source i has any supply left – Otherwise, select x(i+1)j 21

The Northwest Corner Rule Destination Source A B C Dummy Demand N S 16 E 13 100 14 22 17 19 15 200 13 40 9 Supply W 20 300 23 10 10 150 0 0 90 100 140 300 350 150 90 250 Z = 10770 22

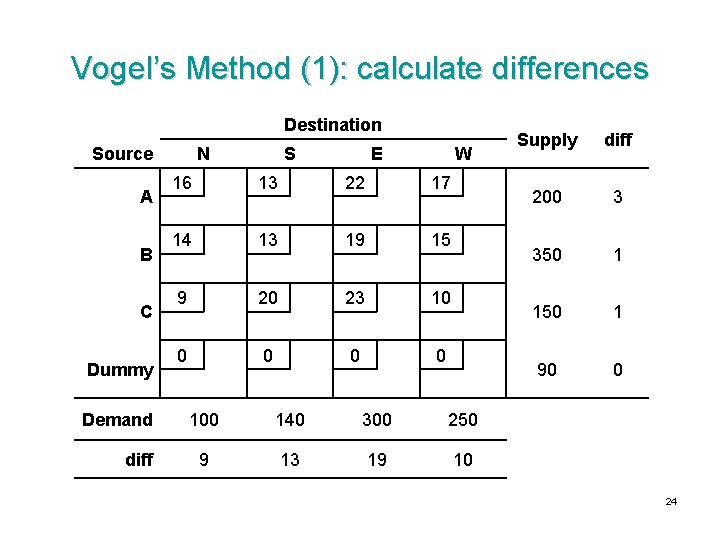
Vogel’s Method • For each row and column, calculate its difference: = (Second smallest cij in row/col) - (Smallest cij in row/col) • For the row/col with the largest difference, select entry with minimum cij as basic • Eliminate any row/col with no supply/demand left from further steps • Repeat until BFS found 23

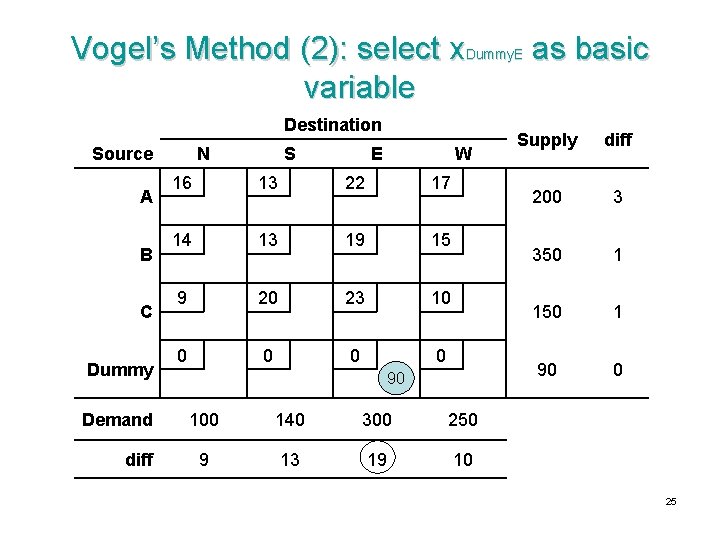
Vogel’s Method (1): calculate differences Destination Source A B C Dummy Demand diff N S E W 16 13 22 17 14 13 19 15 9 20 23 10 0 0 100 140 300 250 9 13 19 10 Supply diff 200 3 350 1 150 1 90 0 24

Vogel’s Method (2): select x. Dummy. E as basic variable Destination Source A B C Dummy Demand diff N S E W 16 13 22 17 14 13 19 15 9 20 23 10 0 0 90 100 140 300 250 9 13 19 10 Supply diff 200 3 350 1 150 1 90 0 25

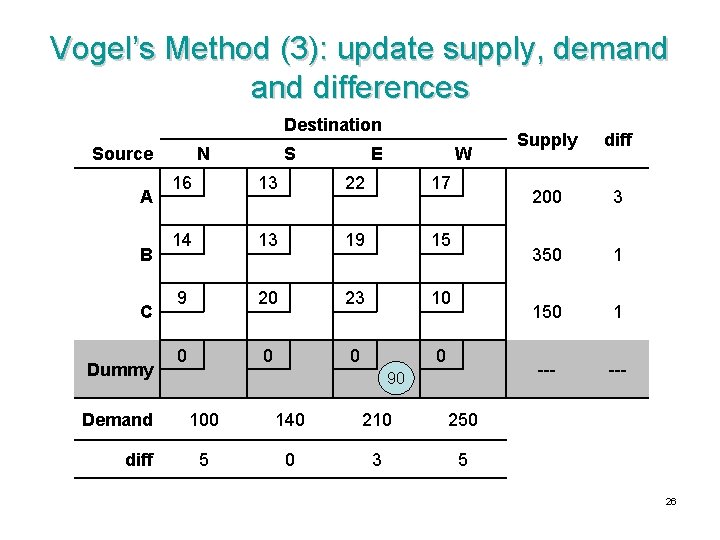
Vogel’s Method (3): update supply, demand differences Destination Source A B C Dummy Demand diff N S E W 16 13 22 17 14 13 19 15 9 20 23 10 0 0 90 100 140 210 250 5 0 3 5 Supply diff 200 3 350 1 150 1 --- 26

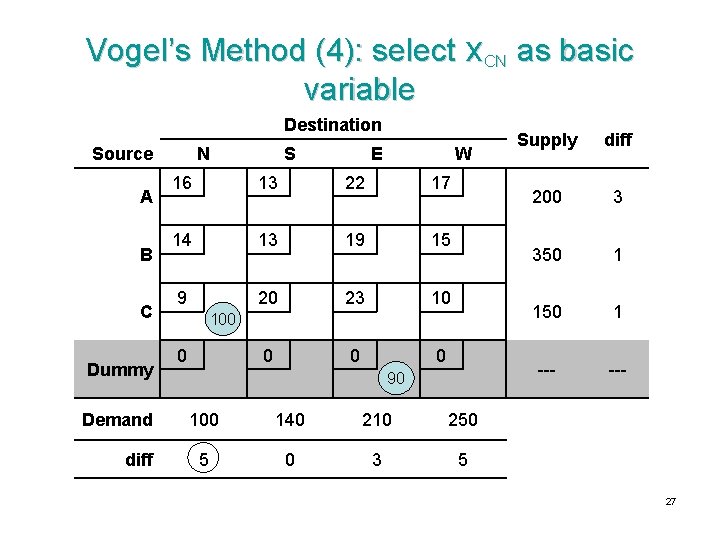
Vogel’s Method (4): select x. CN as basic variable Destination Source A B C Dummy Demand diff N S E W 16 13 22 17 14 13 19 15 9 20 23 10 0 100 0 90 100 140 210 250 5 0 3 5 Supply diff 200 3 350 1 150 1 --- 27

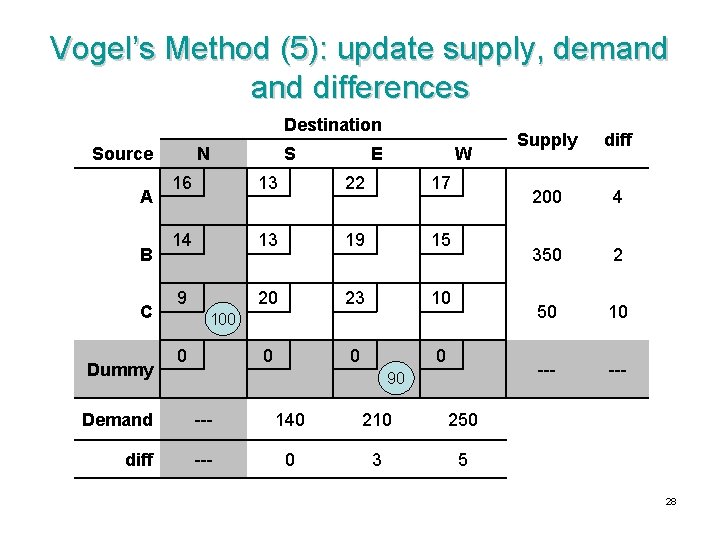
Vogel’s Method (5): update supply, demand differences Destination Source A B C Dummy N S E W 16 13 22 17 14 13 19 15 9 20 23 10 0 100 0 90 Demand --- 140 210 250 diff --- 0 3 5 Supply diff 200 4 350 2 50 10 --- 28

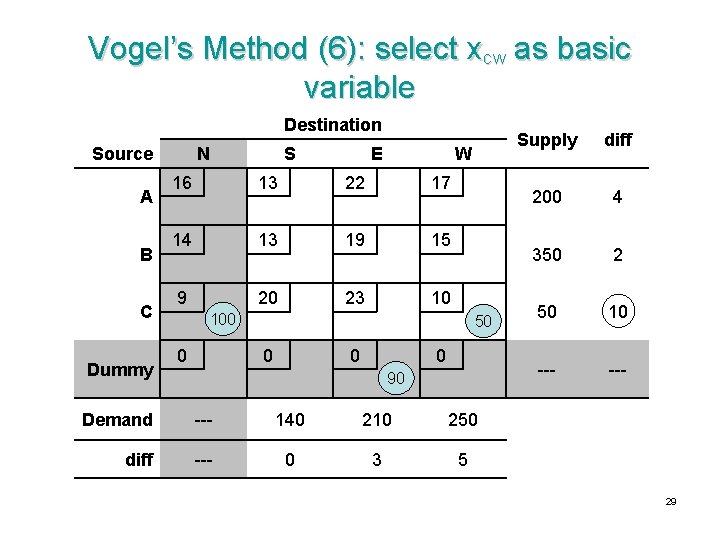
Vogel’s Method (6): select x. CW as basic variable Destination Source A B C Dummy N S E W 16 13 22 17 14 13 19 15 9 20 23 10 100 0 50 0 90 Demand --- 140 210 250 diff --- 0 3 5 Supply diff 200 4 350 2 50 10 --- 29

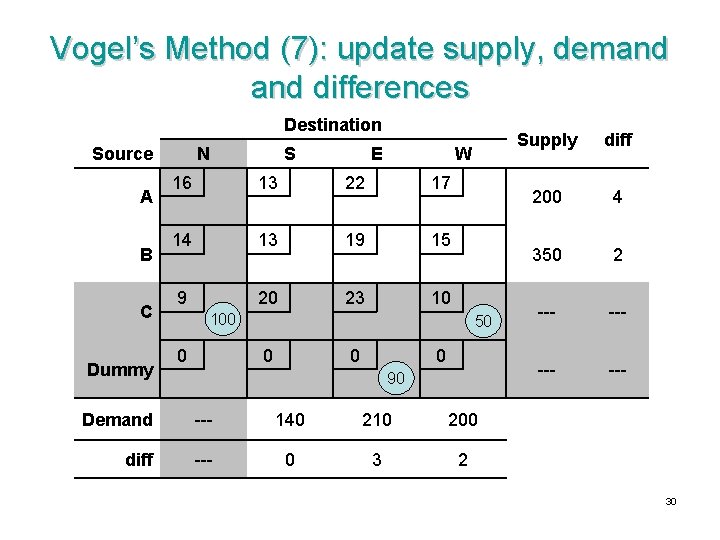
Vogel’s Method (7): update supply, demand differences Destination Source A B C Dummy N S E W 16 13 22 17 14 13 19 15 9 20 23 10 100 0 50 0 90 Demand --- 140 210 200 diff --- 0 3 2 Supply diff 200 4 350 2 --- --- 30

Vogel’s Method (8): select x. AS as basic variable Destination Source A B C Dummy N 16 S E 13 W 22 17 140 14 13 19 15 9 20 23 10 100 0 50 0 90 Demand --- 140 210 200 diff --- 0 3 2 Supply diff 200 4 350 2 --- --- 31

Vogel’s Method (9): update supply, demand differences Destination Source A B C Dummy N 16 S E 13 W 22 17 140 14 13 19 15 9 20 23 10 100 0 50 0 90 Demand --- 210 200 diff --- 3 2 Supply diff 60 5 350 4 --- --- 32

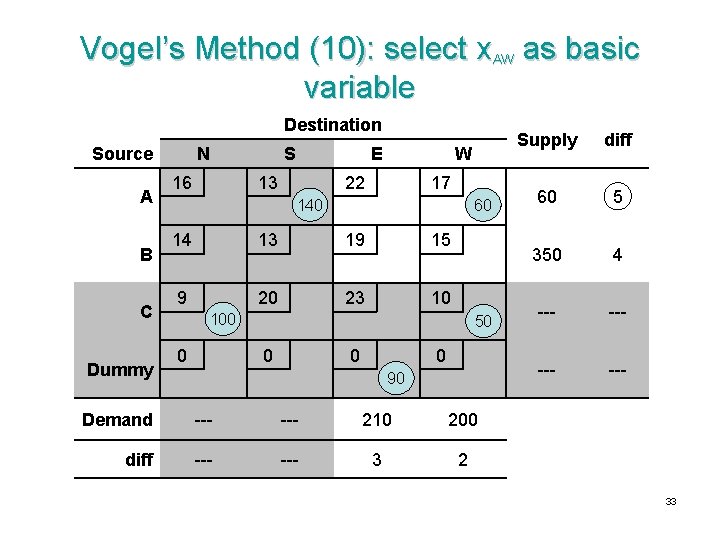
Vogel’s Method (10): select x. AW as basic variable Destination Source A B C Dummy N 16 S E 13 W 22 17 140 60 14 13 19 15 9 20 23 10 100 0 50 0 90 Demand --- 210 200 diff --- 3 2 Supply diff 60 5 350 4 --- --- 33

Vogel’s Method (11): update supply, demand differences Destination Source A B C Dummy N 16 S E 13 W 22 17 140 60 14 13 19 15 9 20 23 10 100 0 50 0 90 Demand --- diff --- 210 Supply diff --- 350 4 --- --- 140 34

Vogel’s Method (12): select x. BW and x. BE as basic variables Destination Source A B C Dummy Demand diff N 16 S E 13 Supply diff 60 --- 140 --- W 22 17 140 14 13 19 15 210 9 20 23 10 100 0 50 0 90 ----- --- --Z = 10330 35

Optimality Test • In the regular simplex method, we needed to check the row-0 coefficients of each nonbasic variable to check optimality and we have an optimal solution if all are 0 • There is an efficient way to find these row-0 coefficients for a given BFS to a transportation problem: – Given the basic variables, calculate values of dual variables • ui associated with each source • vj associated with each destination using cij – ui – vj = 0 for xij basic, or ui + vj = cij (let ui = 0 for row i with the largest number of basic variables) – Row-0 coefficients can be found from c’ij=cij-ui-vj for xij nonbasic 36

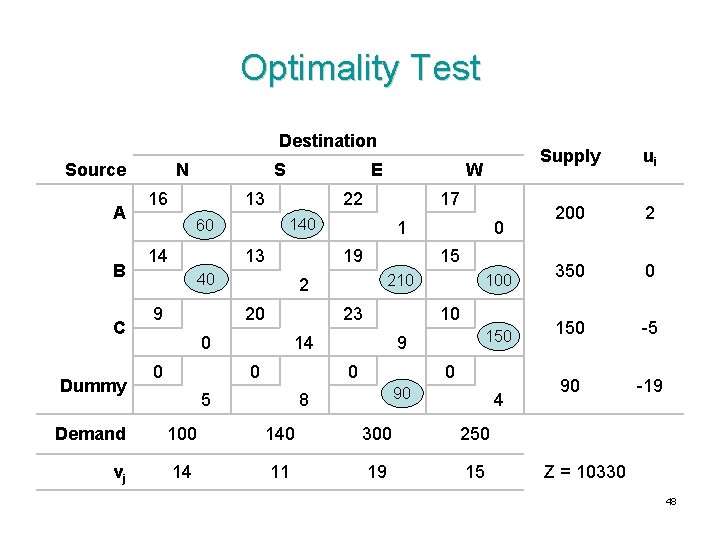
Optimality Test (1) Destination Source A B C Dummy Demand N 16 S 13 E 22 17 19 15 140 14 13 210 9 20 23 0 60 200 140 350 50 10 100 0 Supply W 0 0 90 90 100 140 300 ui 250 vj 37

Optimality Test (2) • Calculate ui, vj using cij – ui – vj = 0 for xij basic (let ui = 0 for row i with the largest number of basic variables) Destination Source A B C Dummy N S 16 E 13 Supply ui 60 200 0 140 350 -2 50 150 -7 90 -21 W 22 17 140 14 9 13 100 0 19 20 210 23 0 15 10 0 90 0 Demand 100 140 300 250 vj 16 13 21 17 38

Optimality Test (3) • Calculate c’ij=cij-ui-vj for xij nonbasic Destination Source A B C Dummy N S 16 E 13 14 22 13 9 0 210 350 -2 50 150 -7 90 -21 9 0 5 140 10 14 0 0 15 23 100 200 1 2 20 60 17 19 0 ui W 140 0 Supply 0 90 8 4 Demand 100 140 300 250 vj 16 13 21 17 39

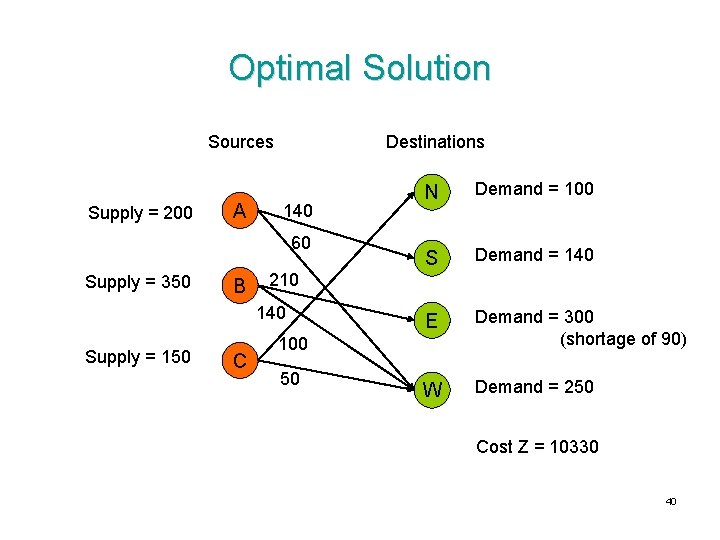
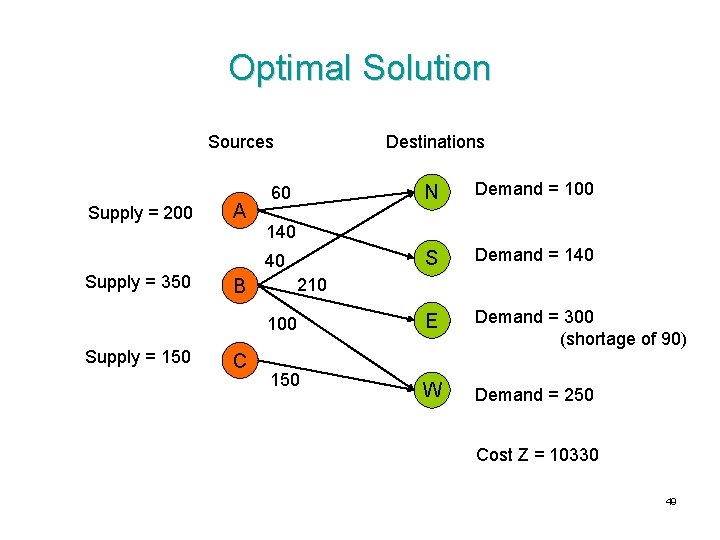
Optimal Solution Sources Supply = 200 A Destinations 140 60 Supply = 350 B 210 140 Supply = 150 C N Demand = 100 S Demand = 140 E Demand = 300 (shortage of 90) W Demand = 250 100 50 Cost Z = 10330 40

An Iteration • Find the entering basic variable – Select the variable with the largest negative c’ij • Find the leaving basic variable – Determine the chain reaction that would result from increasing the value of the entering variable from zero – The leaving variable will be the first variable to reach zero because of this chain reaction 41

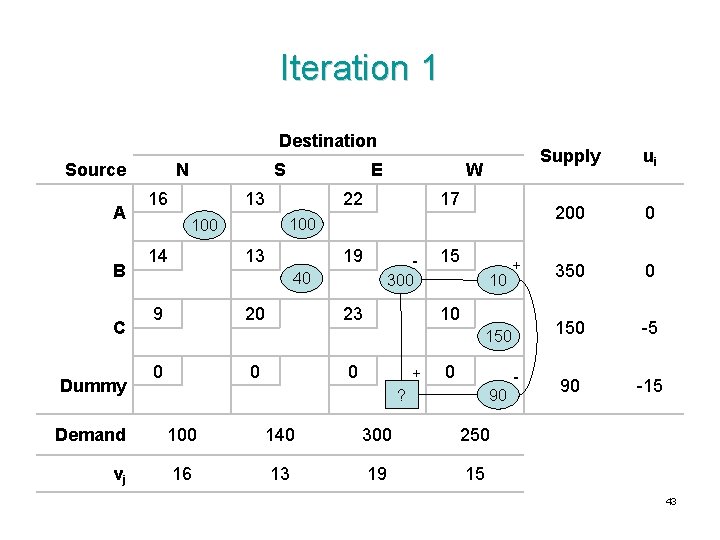
Initial Solution Obtained by the Northwest Corner Rule Destination Source A B C Dummy N S 16 E 13 22 13 40 20 300 150 9 0 -1 10 10 12 0 2 15 23 -2 0 3 19 -2 9 17 100 14 W 0 2 90 -4 Demand 100 140 300 250 vj 16 13 19 15 Supply ui 200 0 350 0 150 -5 90 -15 42

Iteration 1 Destination Source A B C Dummy N S 16 E 13 22 17 100 14 13 19 300 40 9 W 20 23 15 10 + 10 150 0 + 0 - ? 90 Demand 100 140 300 250 vj 16 13 19 15 Supply ui 200 0 350 0 150 -5 90 -15 43

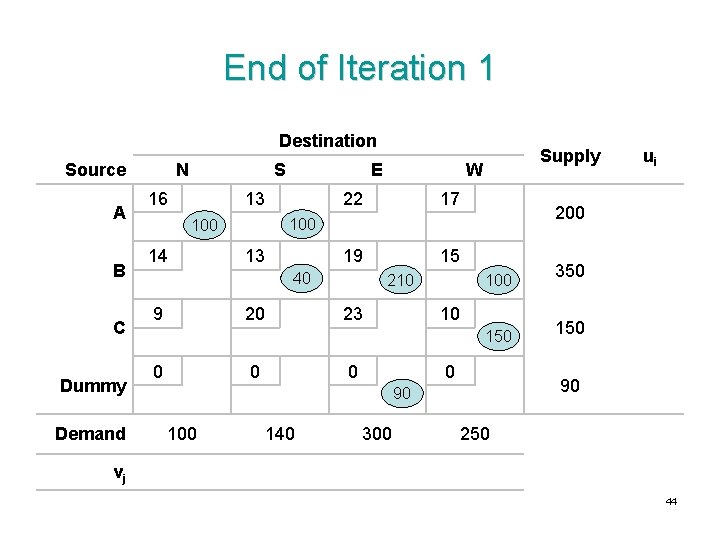
End of Iteration 1 Destination Source A B C Dummy Demand N S 16 E 13 22 17 13 19 15 40 9 20 210 23 100 10 150 0 0 140 300 350 150 90 90 100 ui 200 100 14 Supply W 250 vj 44

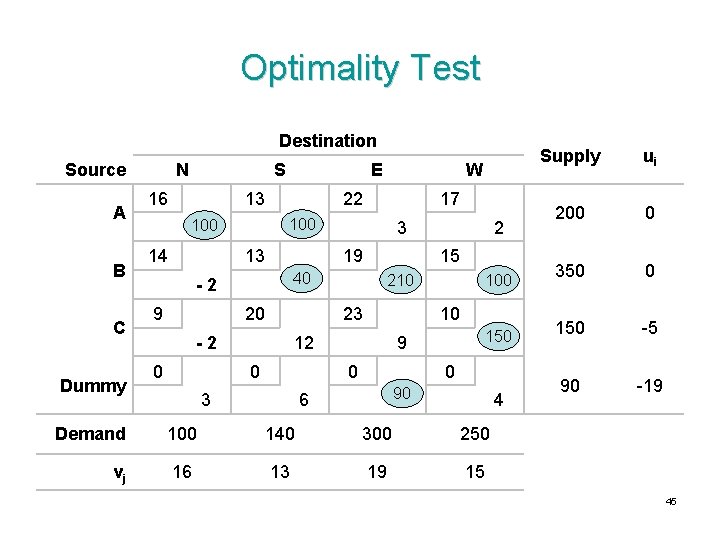
Optimality Test Destination Source A B C Dummy N S 16 E 13 22 13 210 23 -2 150 9 0 3 100 10 12 0 2 15 40 20 0 3 19 -2 9 17 100 14 W 0 90 6 4 Demand 100 140 300 250 vj 16 13 19 15 Supply ui 200 0 350 0 150 -5 90 -19 45

Iteration 2 Destination Source A B C Dummy N S 16 - 13 + 13 ? 9 W + 22 17 - 19 15 100 14 E 210 40 20 23 100 10 150 0 0 90 Demand 100 140 300 250 vj 16 13 19 15 Supply ui 200 0 350 0 150 -5 90 -19 46

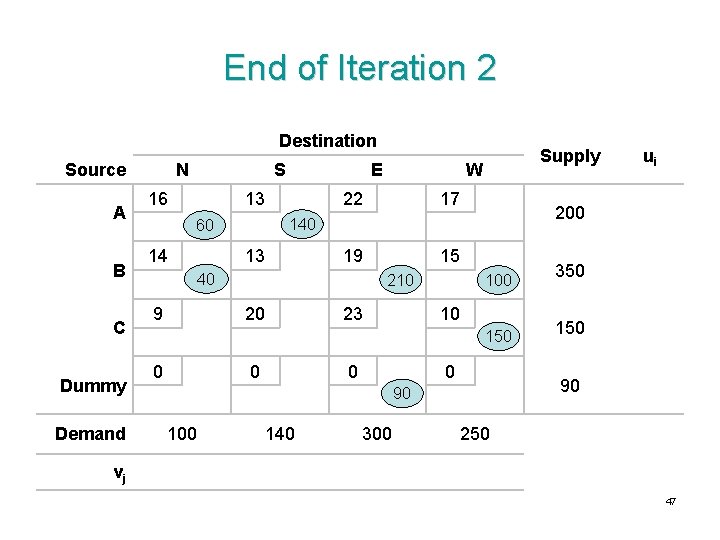
End of Iteration 2 Destination Source A B C Dummy Demand N S 16 E 13 22 17 13 19 15 40 9 210 20 23 100 10 150 0 0 140 300 350 150 90 90 100 ui 200 140 60 14 Supply W 250 vj 47

Optimality Test Destination Source A B C Dummy N S 16 E 13 22 13 210 23 0 150 9 0 5 100 10 14 0 0 15 2 20 0 1 19 40 9 17 140 60 14 W 0 90 8 4 Demand 100 140 300 250 vj 14 11 19 15 Supply ui 200 2 350 0 150 -5 90 -19 Z = 10330 48

Optimal Solution Sources Supply = 200 A Destinations 60 C S Demand = 140 E Demand = 300 (shortage of 90) W Demand = 250 210 B 100 Supply = 150 Demand = 100 140 40 Supply = 350 N 150 Cost Z = 10330 49

The Assignment Problem • The problem of finding the minimum-costly assignment of a set of tasks (i=1, …, m) to a set of agents (j=1, …, n) • Each task should be performed by one agent • Each agent should perform one task • A cost cij associated with each assignment • We should have m=n (if not…? ) • A special type of linear programming problem, and • A special type of transportation problem, with si=dj= ? 50

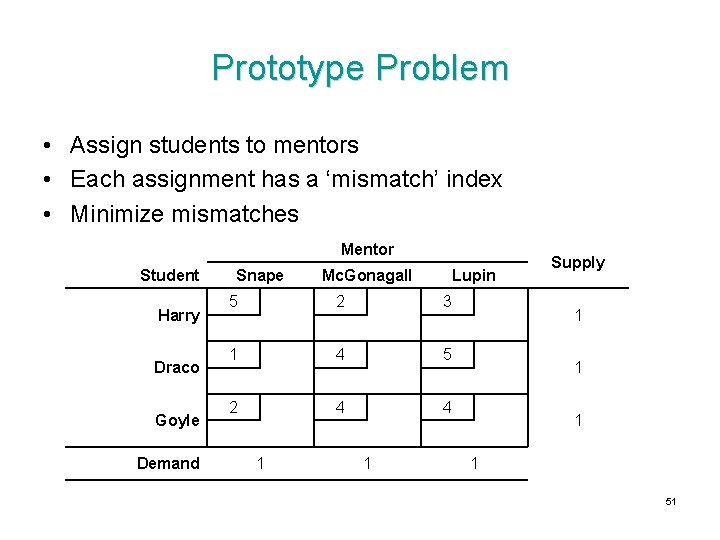
Prototype Problem • Assign students to mentors • Each assignment has a ‘mismatch’ index • Minimize mismatches Mentor Student Harry Draco Goyle Demand Snape Mc. Gonagall Lupin 5 2 3 1 4 5 2 4 4 1 1 Supply 1 1 51

Prototype Problem • Linear programming formulation Let xij denote… Minimize subject to 52

General LP Formulation for Assignment Problems 53

Solving the Assignment Problem • It is a linear programming problem, so we could use regular simplex method • It is a transportation problem, so we could use transportation simplex method • However, it has a very special structure, such that it can be solved in polynomial time • Many such algorithms exist, but the best known (and one of the oldest) is the Hungarian Method 54

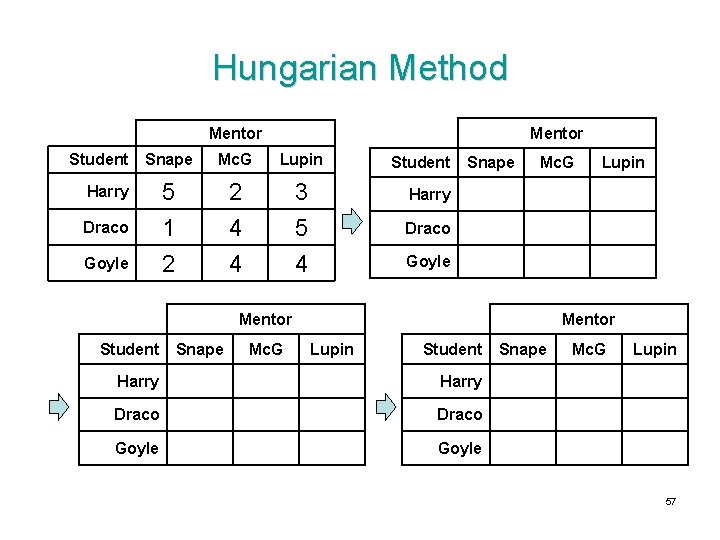
The Hungarian Method 1. 2. 3. 4. 5. Subtract row minimums from each element in the row Subtract column minimums from each element in the column Cover the zeroes with as few lines as possible If the number of lines = n, then optimal solution is hidden in zeroes Otherwise, find the minimum cost that is not covered by any lines 1. Subtract it from all uncovered elements 2. Add it to all elements at intersections (covered by two lines) 6. Back to step 3 55

The Hungarian Method – Optimal Solution How to identify the optimal solution: • Make the assignments one at a time in positions that have zero elements. • Begin with rows or columns that have only one zero. Cross out both the row and the column involved after each assignment is made. • Move on to the rows and columns that are not yet crossed out to select the next assignment, with preference given to any such row or column that has only one zero that is not crossed out. • Continue until every row and every column has exactly one assignment and so has been crossed out. 56

Hungarian Method Mentor Student Snape Mc. G Lupin 5 1 2 2 4 4 3 5 4 Harry Draco Goyle Student Snape Mc. G Harry Draco Goyle Mentor Student Snape Mc. G Lupin Mentor Lupin Student Harry Draco Goyle Snape Mc. G Lupin 57