Operasjonsanalytiske emner Del 5 Transportmodeller Med variasjoner LP

Operasjonsanalytiske emner Del 5 Transportmodeller Med variasjoner LP modeller for transportproblemer BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 1

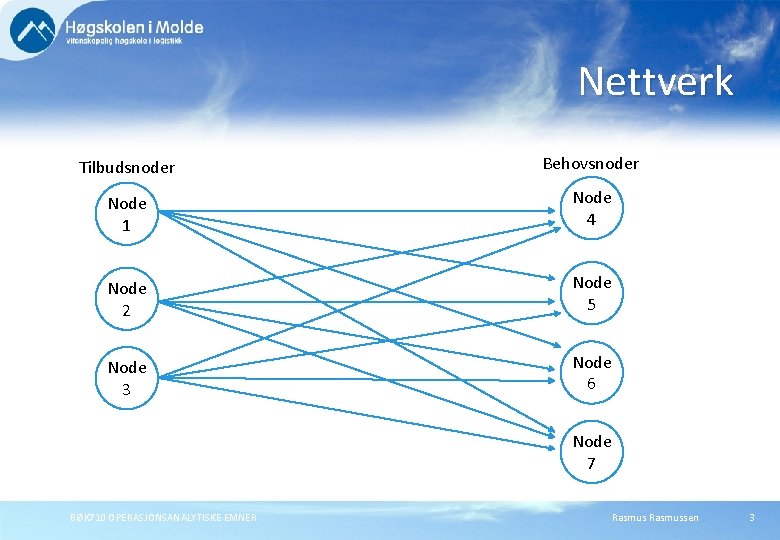
Innledning Transportmodeller representer problemer der en skal transportere f. eks. varer fra en kilde (lager, fabrikk, etc. ) til et bestemmelsessted (f. eks. kunder). En vanlig måte å beskrive slike problemer er ved hjelp av nettverk. Et nettverk består av noder og greiner. Nodene angis med sirkler og representerer ofte ressurser og behov. Greiene angir mulige koblinger mellom nodene. Nettverket er en prinsippskisse, og angir for eksempel ikke geografiske proporsjoner. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 2

Nettverk Tilbudsnoder Behovsnoder Node 1 Node 4 Node 2 Node 5 Node 3 Node 6 Node 7 BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 3

Symboler Parametere: l Antall tilbudsnoder k Antall kundenoder L K G ai bj cf, t Mengden av tilbudsnoder Mengden av kundenoder Mengden av greiner Kapasitet hos kilde i Behov hos kunde j Enhetskostnad fra node f til node t L = {1, 2, …, l} K = {l+1, …, l+k} G = {(L×K)} i {L} j {K} (f, t) {G} Beslutningsvariabler: Xf, t Antall enheter sendt av varen fra node f til node t BØK 710 OPERASJONSANALYTISKE EMNER (f, t) {G} Rasmussen 4

Eksempel på et transportproblem MG Auto har tre fabrikker i Los Angeles, Detroit og New Orleans. De skal forsyne to distribusjonssentra i Denver og Miami. Los Angeles Detroit New Orleans Behov Transportkostnader Denver Miami 80, 215, 100, 108, 102, 2300 68, 1400 Kapasitet 1000 1500 1200 En ønsker å dekke behovet på billigste måte, samtidig som kapasitetene ikke må overskrides. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 5

Nettverk Distribusjonssenter Bilfabrikk Los Angeles a 1 = 1000 Detroit a 2 = 1500 Node 1 Node 2 c 1, 4 = 80, c 1, 5 = 215, c 2, 4 = 100, - a 3 = 1200 Node 3 Node 4 Denver Node 5 Miami b 4 = 2300 c 2, 5 = 108, c 3, 4 = 102, - New Orleans X 1, 4 = ? b 5 = 1400 c 3, 5 = 68, - Hvor mye skal transporteres fra de ulike bilfabrikkene til de ulike distribusjonssentraene, slik at kostnadene blir minst mulig? BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 6

Målfunksjon: Matematisk formulering Minimer totalsummen av pris∙mengde (cf, t∙Xf, t) for alle greiner i nettverket. Alternativ formulering: Min Z= 80 X 1, 4 + 215 X 1, 5 + 100 X 2, 4 + 108 X 2, 5 + 102 X 3, 4 + 68 X 3, 5 BØK 710 OPERASJONSANALYTISKE EMNER Merk at minimering av kostnader forutsetter at inntektene ikke påvirkes av beslutningene. For å unngå den trivielle null-løsningen (ikke transportere noe), så må en dessuten anta at leveringsrestriksjonene enten er «=» eller « » . Rasmussen 7

Matematisk formulering Restriksjoner: Sum mengde levert fra alle tilbudsnoder (f L) til en behovsnode (j), dvs. sum mengde varer en behovsnode mottar, må minst dekke behovet noden har, bj. Kravet gjelder for alle behovsnoder (j K). Alternativ formulering: Denver: Miami: X 14 X 15 + X 24 + X 25 BØK 710 OPERASJONSANALYTISKE EMNER + X 34 + X 35 ≥ 2300 ≥ 1400 Sum leveranser til node 4 Sum leveranser til node 5 Rasmussen 8

Matematisk formulering Restriksjoner: Sum leveranser fra en tilbudsnode (i) til alle behovsnoder (t K) kan ikke overstige tilbudsnodens kapasitet. Dette kravet må gjelde for alle tilbudsnoder (i L). Alternativ formulering: Los Angeles: Detroit: New Orleans: X 14 X 24 X 34 + X 15 + X 25 + X 35 ≤ 1000 ≤ 1500 ≤ 1200 Sum levert fra node 1 Sum levert fra node 2 Sum levert fra node 3 Ikke-negativitetsbetingelsene: Xf, t ≥ 0 for alle (f, t) G BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 9

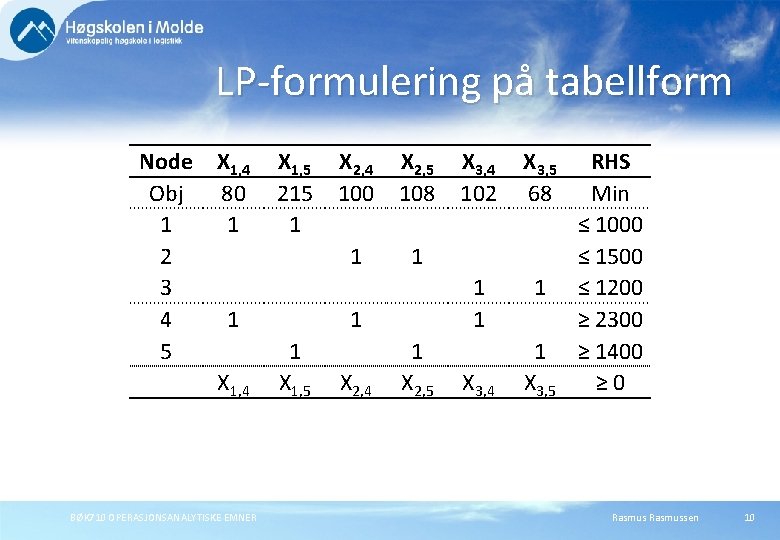
LP-formulering på tabellform Node X 1, 4 Obj 80 1 1 2 3 4 1 5 X 1, 4 BØK 710 OPERASJONSANALYTISKE EMNER X 1, 5 215 1 X 2, 4 100 X 2, 5 108 1 1 X 1, 5 X 2, 4 1 X 2, 5 X 3, 4 102 X 3, 5 68 1 1 1 X 3, 4 1 X 3, 5 RHS Min ≤ 1000 ≤ 1500 ≤ 1200 ≥ 2300 ≥ 1400 ≥ 0 Rasmussen 10

Regneark med layout lik LP modell Samme formel kopieres til alle restriksjonene Celle I 4 Formel =SUMPRODUCT($C$3: $H$3; C 4: H 4) Kopieres til I 5: I 9 Her er regnearket organisert med lay-out identisk LP-modellen. Linje 3 angir verdien til beslutningsvariablene (kolonne C: H) Linje 4 angir koeffisientene i målfunksjonen (objective) Linje 5: 7 angir restriksjonene for node 1 -3 (fabrikker) Linje 8: 9 gir det restriksjonene for node 4 -5 (distribusjonslager) Kolonne I angir venstresiden av restriksjonene, samt totalverdien av målfunksjonen. Kolonne K angir høyresiden av restriksjonene. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 11

Regneark organisert rundt dataene Her er tabellen med data kopiert for å gi plass til beslutningsvariablene, restriksjonene, og målfunksjonen. Celle Formel E 11 =SUM(C 11: D 11) E 14 =SUMPRODUCT(C 4: D 6; C 11: D 13) C 14 BØK 710 OPERASJONSANALYTISKE EMNER =SUM(C 11: C 13) Kopieres til E 12: E 13 D 14 LP modellen er nøyaktig den samme. Men lay-out er tilpasset problemet, og organisert rundt dataene. Rasmussen 12

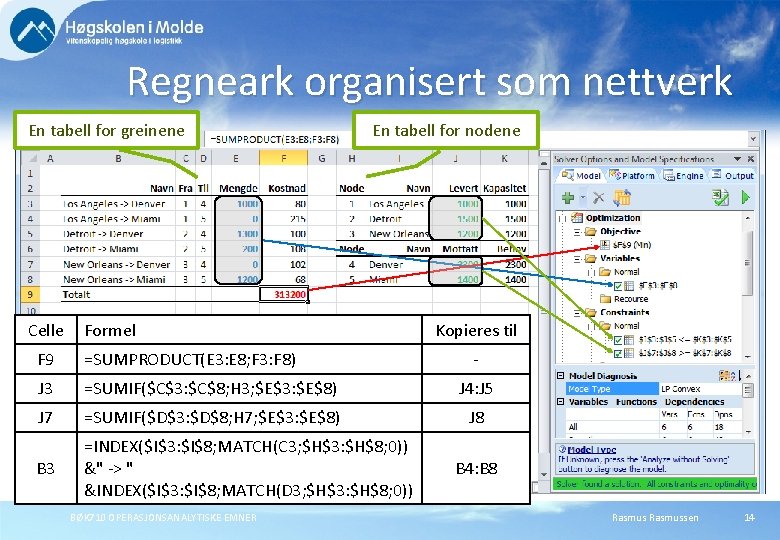
Kjennetegn ved nettverk Om vi ser på vår figur, kan vi oppsummere følgende: Vi har en beslutningsvariabel for hver grein (Xft) Vi har en restriksjon for hver node; kapasitetsrestriksjoner for alle lagernoder behovsrestriksjoner for alle kundenoder En effektiv måte å organisere regnearket er derfor å lage to tabeller: En tabell for beslutningsvariablene (greinene) greinene En tabell for restriksjonene (nodene) nodene BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 13

Regneark organisert som nettverk En tabell for greinene Celle En tabell for nodene Formel Kopieres til F 9 =SUMPRODUCT(E 3: E 8; F 3: F 8) J 3 =SUMIF($C$3: $C$8; H 3; $E$3: $E$8) J 4: J 5 J 7 =SUMIF($D$3: $D$8; H 7; $E$3: $E$8) J 8 B 3 =INDEX($I$3: $I$8; MATCH(C 3; $H$3: $H$8; 0)) &" -> " &INDEX($I$3: $I$8; MATCH(D 3; $H$3: $H$8; 0)) BØK 710 OPERASJONSANALYTISKE EMNER - B 4: B 8 Rasmussen 14

Balansering av nettverksmodeller Når totalt tilbud er lik total etterspørsel, har vi en balansert transportmodell. Restriksjonene kan da være på likhetsform (=). Hvis totalt tilbud overstiger total etterspørsel, vil det alltid finnes en mulig løsning. Vi vil da ikke benytte full kapasitet i tilbudsnodene. Vi kan da la etterspørselsnoder ha restriksjoner på formen ≥. Hvis totalt tilbud er mindre enn total etterspørsel, har vi et uløselig problem, om målfunksjonen er minimering. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 16

Restordrer Om totalt tilbud ikke kan dekke total etterspørsel, må vi innføre restordrer, hvis målfunksjonen er minimering. For maksimeringsproblem bestemmes restordrer automatisk, vi leverer ikke til de minst lønnsomme kundene. Minimeringsproblemer må løses i to trinn: Først minimeres totalt antall restordrer. Så minimeres kostnadene, men slik at totalt antall restordrer ikke overstiger minimum restordrer totalt. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 17

Eksempel på underkapasitet MG Auto har tre fabrikker i Los Angeles, Detroit og New Orleans. De skal forsyne to distribusjonssentra i Denver og Miami. Los Angeles Detroit New Orleans Behov Transportkostnader Denver Miami 80, 215, 100, 108, 102, 2300 68, 1400 Kapasitet 1000 1300 1200 En ønsker å dekke mest mulig av behovet på billigste måte, samtidig som kapasitetene ikke må overskrides. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 18

Målfunksjon: Trinn 1 – Minimere restordrer Minimer mengde restordrer totalt for alle kunder (j K). Alternativ formulering: Min W = R 4 + R 5 Variabelen Rj angir altså restordrer til kunde j. Om restordrer er «gratis» , så vil all etterspørsel bli restordrer. For å unngå en slik null-løsning må vi sette som betingelse at sum leveranser + restordrer minst tilsvarer etterspørselen, for hver kunde. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 19

Restriksjoner: Trinn 1 – Minimere restordrer Sum mengde levert fra alle tilbudsnoder (f L) til en behovsnode (j), dvs. sum mengde varer en behovsnode mottar, pluss restordrer, må minst dekke behovet noden har, bj. Kravet gjelder for alle behovsnoder (j K). Alternativ formulering: Denver: Miami: X 14 + X 24 + X 34 + R 4 ≥ 2300 Sum leveranser til node 4, inklusive restordrer X 15 + X 25 + X 35 + R 5 ≥ 1400 Sum leveranser til node 5, inklusive restordrer BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 20

Restriksjoner: Trinn 1 – Minimere restordrer Sum leveranser fra en tilbudsnode (i) til alle behovsnoder (t K) kan ikke overstige tilbudsnodens kapasitet. Dette kravet må gjelde for alle tilbudsnoder (i L). Alternativ formulering: Los Angeles: Detroit: New Orleans: X 14 X 24 X 34 + X 15 + X 25 + X 35 ≤ 1000 ≤ 1300 ≤ 1200 Sum levert fra node 1 Sum levert fra node 2 Sum levert fra node 3 Ikke-negativitetsbetingelsene: Xf, t ≥ 0 for alle (f, t) G, og Rj ≥ 0 for alle j K. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 21

Trinn 2 – Minimere kostnader I trinn 1 har vi funnet den løsning som dekker mest mulig av behovet, dvs. vi har funnet minimum mengde restordrer. Kall optimal verdi på målfunksjonen W*. Men vi har så langt ignorert kostnadene. Den løsningen vi har funnet i trinn 1 kan altså være en løsning som gir svært høye kostnader, og det er mulig at det finnes løsninger med lavere kostnad som har samme mengde restordrer. I trinn 2 skal vi derfor forsøke å finne alternative løsninger med samme total mengde restordrer W*, men som har en lavere kostnad. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 22

Målfunksjon: Trinn 2 – Minimere kostnader Minimer totalsummen av pris∙mengde (cf, t∙Xf, t) for alle greiner i nettverket. Alternativ formulering: Min Z = 80 X 1, 4 + 215 X 1, 5 + 100 X 2, 4 + 108 X 2, 5 + 102 X 3, 4 + 68 X 3, 5 BØK 710 OPERASJONSANALYTISKE EMNER Merk at minimering av kostnader forutsetter at inntektene ikke påvirkes av beslutningene. For å unngå den trivielle null-løsningen (ikke transportere noe), så må en dessuten anta at leveringsrestriksjonene enten er «=» eller « » . Rasmussen 23

Restriksjoner: Trinn 2 – Minimere kostnader Sum mengde levert fra alle tilbudsnoder (f L) til en behovsnode (j), dvs. sum mengde varer en behovsnode mottar, pluss restordrer, må minst dekke behovet noden har, bj. Kravet gjelder for alle behovsnoder (j K). Alternativ formulering: Denver: Miami: X 14 + X 24 + X 34 + R 4 ≥ 2300 Sum leveranser til node 4, inklusive restordrer X 15 + X 25 + X 35 + R 5 ≥ 1400 Sum leveranser til node 5, inklusive restordrer BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 24

Restriksjoner: Trinn 2 – Minimere kostnader Sum leveranser fra en tilbudsnode (i) til alle behovsnoder (t K) kan ikke overstige tilbudsnodens kapasitet. Dette kravet må gjelde for alle tilbudsnoder (i L). Alternativ formulering: Los Angeles: Detroit: New Orleans: X 14 X 24 X 34 + X 15 + X 25 + X 35 BØK 710 OPERASJONSANALYTISKE EMNER ≤ 1000 ≤ 1300 ≤ 1200 Sum levert fra node 1 Sum levert fra node 2 Sum levert fra node 3 Rasmussen 25

Restriksjoner: Trinn 2 – Minimere kostnader Sum restordrer må være mindre eller lik minimum sum restordrer totalt. Alternativ formulering: R 4 + R 5 ≤ W* Sum restordrer til node 4 og node 5 Ikke-negativitetsbetingelsene: Xf, t ≥ 0 for alle (f, t) G, og Rj ≥ 0 for alle j K. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 26

Trinn 1 – Minimere restordrer Celle Formel Kopieres til F 9 =SUMPRODUCT(E 3: E 8; F 3: F 8) J 3 =SUMIF($C$3: $C$8; H 3; $E$3: $E$8) J 4: J 5 J 7 =SUMIF($D$3: $D$8; H 7; $E$3: $E$8) J 8 K 9 =SUM(K 7: K 8) - L 7 =J 7+K 7 BØK 710 OPERASJONSANALYTISKE EMNER - L 8 Rasmussen 27

Trinn 2 – Minimere kostnader Celle Formel Kopieres til F 9 =SUMPRODUCT(E 3: E 8; F 3: F 8) J 3 =SUMIF($C$3: $C$8; H 3; $E$3: $E$8) J 4: J 5 J 7 =SUMIF($D$3: $D$8; H 7; $E$3: $E$8) J 8 K 9 =SUM(K 7: K 8) - L 7 =J 7+K 7 BØK 710 OPERASJONSANALYTISKE EMNER - L 8 Rasmussen 28

Ubalanserte nettverksmodeller Generelt sett er det umulig på forhånd å bestemme om en nettverksmodell har en balansert løsning. Det kan f. eks. skyldes at total kapasitet deles på flere ulike produkter, og en kan derfor ikke på forhånd vite hvor mye kapasitet som er tilgjengelig for de ulike produktgruppene. Det kan også skyldes svinn underveis langs greinene (f. eks. transport av gass i en rørledning), og det er umulig å vite hvor stort svinnet er før en vet hvordan transporten skal foregå. Hvis en modell ikke lar seg løse uten restordrer må en altså i ettertid modifisere modellen og løse den i to trinn. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 29

Transport over tid (lager) Boralis produserer ryggsekker, og bruker deltidsansatte for å tilpasse produksjonen til sesongetterspørselen. Måned Etterspørsel Kapasitet Mars 100 50 April 200 180 Mai 180 280 Juni 300 270 1. Variable produksjonskostnader er kr. 40, - pr. sekk. 2. Lagerkostnader er kr. 0, 50 pr. sekk pr. måned. 3. Etterleveringskostnader er kr. 2, - pr. sekk pr. måned. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 30

Nettverk – Transport over tid (lager) Mars April IB lager Mai IB lager Tilgang Produksjon Etterspørsel BØK 710 OPERASJONSANALYTISKE EMNER Produksjon Etterspørsel Udekket Tilgang Salg Udekket IB lager Tilgang Salg Juni Salg Etterspørsel Udekket Rasmussen 31

Symboler Parametere: Et Etterspørsel i periode t Kt Produksjonskapasitet i periode t c Enhetskostnad pr. produsert enhet l Lagerkostnad pr. enhet pr. periode b Etterleveringskostnad pr. enhet pr. periode IBXt Inngående lagerbeholdning periode t UBXt Utgående lagerbeholdning periode t IBEt Inngående udekket etterspørsel periode t UBEt Utgående udekket etterspørsel periode t Beslutningsvariabler: Xt St Antall enheter produsert i periode t Antall enheter solgt i periode t BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 32

Målfunksjon: Matematisk formulering Minimer totalsummen av produksjonskostnader, lagerkostnader og etterleveringskostnader i hele planperioden. Alternativ formulering: Min Z = 40 X 3 + 40 X 4 + 40 X 5 + 40 X 6 + 0, 5 UBX 3 + 0, 5 UBX 4 + 0, 5 UBX 5 + 0, 5 UBX 6 + 2 UBE 3 + 2 UBE 4 + 2 UBE 5 + 2 UBE 6 BØK 710 OPERASJONSANALYTISKE EMNER Antar at lager- og etterleveringskostnader er forbundet med overførsel fra en periode til neste. (Kunne også bruk gjennomsnittslager, e. l. ) Rasmussen 33

Matematisk formulering Restriksjoner: Produsert mengde må være mindre eller lik kapasiteten. Kravet gjelder i alle perioder. Mars April Mai Juni X 3 X 4 X 5 X 6 ≤ 50 ≤ 180 ≤ 270 Produksjon mars Produksjon april Produksjon mai Produksjon juni Merk at når produksjon og salg er fastsatt, så er størrelsen på lageret entydig definert. Disse likhetsrestriksjonene som definerer lager kan i regnearket derfor angis som formler, istedenfor å angi de som beslutningsvariabler. IB lager + produksjon – salg = UB lager forrige periode = IB lager inneværende periode BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 34

Restriksjoner: Matematisk formulering IB udekket etterspørsel + ny etterspørsel – salg = UB udekket etterspørsel forrige periode = IB udekket etterspørsel inneværende periode Vi må også ha restriksjoner som sikrer at salget ikke overstiger lageret, og at salget ikke overstiger etterspørselen. Dette kan vi ta hensyn til ved å kreve at UB lager skal være ikke-negativ (da forhindrer vi at salget overstiger IB lager + produksjon), og ved å kreve at UB udekket etterspørsel skal være ikke-negativ (da forhindrer vi at salget overstiger IB udekket etterspørsel + ny etterspørsel). Ikke-negativitetsbetingelsene: Xt, St, UBXt, UBEt ≥ 0 for alle t. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 35

Restriksjoner: Matematisk formulering UB udekket etterspørsel ved utgangen av planperioden = sum etterspørsel – sum produksjonskapasitet, hvis dette er større enn 0, ellers 0. Denne restriksjonen er bare nødvendig ved minimeringsproblem, for å forhindre null-løsningen. Denne betingelsen sikrer at så mye som mulig av etterspørselen dekkes. Ved maksimeringsproblem er denne betingelsen overflødig, modellen vil da automatisk dekke så mye av etterspørselen som det er lønnsomt å dekke. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 36

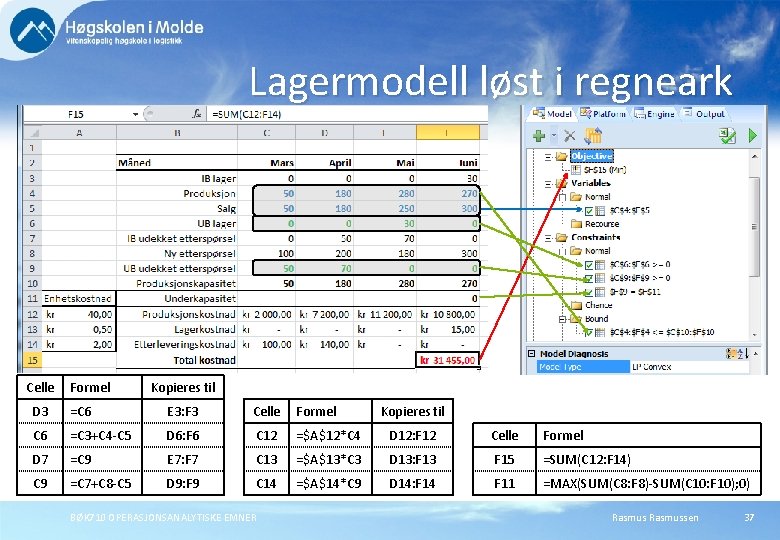
Lagermodell løst i regneark Celle Formel Kopieres til D 3 =C 6 E 3: F 3 Celle Formel C 6 =C 3+C 4 -C 5 D 6: F 6 C 12 =$A$12*C 4 D 12: F 12 Celle Formel D 7 =C 9 E 7: F 7 C 13 =$A$13*C 3 D 13: F 13 F 15 =SUM(C 12: F 14) C 9 =C 7+C 8 -C 5 D 9: F 9 C 14 =$A$14*C 9 D 14: F 14 F 11 =MAX(SUM(C 8: F 8)-SUM(C 10: F 10); 0) BØK 710 OPERASJONSANALYTISKE EMNER Kopieres til Rasmussen 37

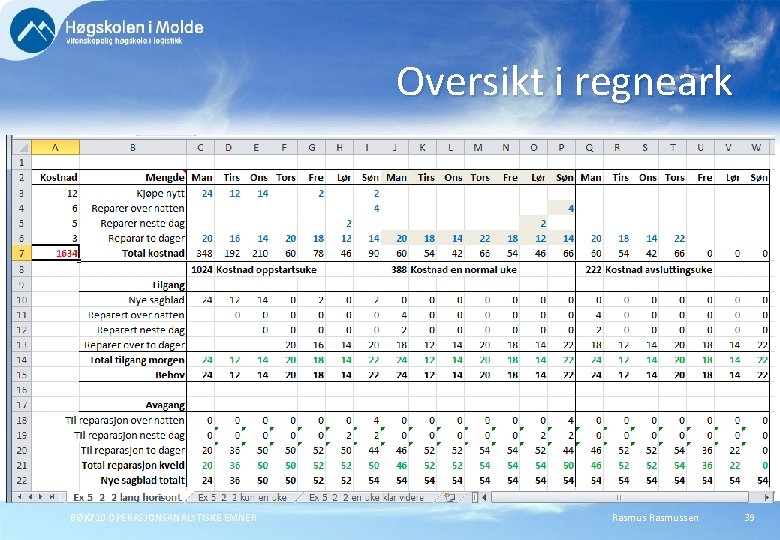
Transport over tid (verktøykapasitet) Arkansas Pacific driver et sagbruk. Sagbladene slites avhengig av type tømmer og mengde som sages. Daglig behov for nyslipte sagblad er som følger: Ukedag Mandag Tirsdag Onsdag Torsdag Fredag Lørdag Søndag Behov 24 12 14 20 18 14 22 Behovet kan dekkes på fire ulike måter: 1. Kjøpe nye blad til en kostnad av kr. 12, - pr. stk. 2. Sliping over natten, kr. 6, - pr. stk. 3. Sliping neste dag, kr. 5, - pr. stk. 4. Sliping over to dager, kr. 3, - pr. stk. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 38

Oversikt i regneark BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 39

Parametere: cn Enhetskostnad for nye sagblad co Enhetskostnad for slipte blad over natten c 1 Enhetskostnad for slipte blad over 1 dag c 2 Enhetskostnad for slipte blad over 2 dager Bt Behov for sagblad dag t Kt Kapasitet, tilgjengelige nyslipte sagblad dag t St Avgang, til sliping etter dag t Rt Totalt antall sagblad innkjøpt , inkludert dag t Beslutningsvariabler: XNt Antall nye sagblad innkjøpt dag t (morgen) XOt Antall sagblad levert til sliping over natten, dag t (kveld) X 1 t Antall sagblad levert til sliping over en dag, dag t (kveld) X 2 t Antall sagblad levert til sliping over to dager, dag t (kveld) BØK 710 OPERASJONSANALYTISKE EMNER Symboler Strengt tatt ikke parametere, siden de er funksjoner av beslutningsvariablene. Rasmussen 40

Målfunksjon: Matematisk formulering Minimer totalsummen av nye sagblad og sliping av gamle sagblad i hele perioden. Alternativ formulering: Min Z = 12 XN 1 + 12 XN 2 + 12 XN 3 + 12 XN 4 + 6 XO 1 + 6 XO 2 + 6 XO 3 + 6 XO 4 + 5 X 11 + 5 X 12 + 5 X 13 + 5 X 14 + 3 X 21 + 3 X 22 + 3 X 23 + 3 X 24 BØK 710 OPERASJONSANALYTISKE EMNER … + 12 XNT … + 6 XOT … + 5 X 1 T … + 3 X 2 T Rasmussen 41

Matematisk formulering Restriksjoner: Tilgjengelige sagblad er nye blad, blad til sliping over natten fra dagen før, til sliping over en dag fra to dager før, og blad til sliping over to dager fra tre dager før. K 1 K 2 K 3 K 4 = = XN 1 XN 2 + XO 1 XN 3 + XO 2+ X 11 XN 4 + XO 3+ X 12+ X 21 K 5 = XN 5 + XO 4+ X 13+ X 22 K 6 = XN 6 + XO 5+ X 14+ X 23 : : : Antall tilgjengelige sagblad må minst dekke behovet K 1 K 2 K 3 K 4 24 12 14 20 Mandag Tirsdag Onsdag Torsdag BØK 710 OPERASJONSANALYTISKE EMNER K 5 K 6 K 7 K 8 18 14 22 24 Fredag Lørdag Søndag Mandag Rasmussen 42

Restriksjoner: Matematisk formulering Sagblad til sliping er blad til sliping over natten; blad til sliping over en dag, fra i dag og i går; og blad til sliping over to dager, fra de tre siste dager. S 1 S 2 S 3 S 4 = = XO 1 + X 11+ X 21 XO 2 + X 11+ X 22+ X 21 XO 3 + X 12+ X 23+ X 22 + X 21 XO 4 + X 13+ X 24+ X 23 + X 22 S 5 = XO 5 + X 14+ X 25+ X 24 + X 23 : : : Antall innkjøpte sagblad fram til tidspunkt t R 1 = XN 1 R 2 = XN 1+ XN 2 BØK 710 OPERASJONSANALYTISKE EMNER R 3 = XN 1+ XN 2+ XN 3 : : : Rasmussen 43

Matematisk formulering Restriksjoner: Antall sagblad til sliping kan ikke overstige antall sagblad innkjøpt totalt. Ikke-negativitetsbetingelsene: XNt , XOt, X 1 t , X 2 t ≥ 0 for alle t BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 44

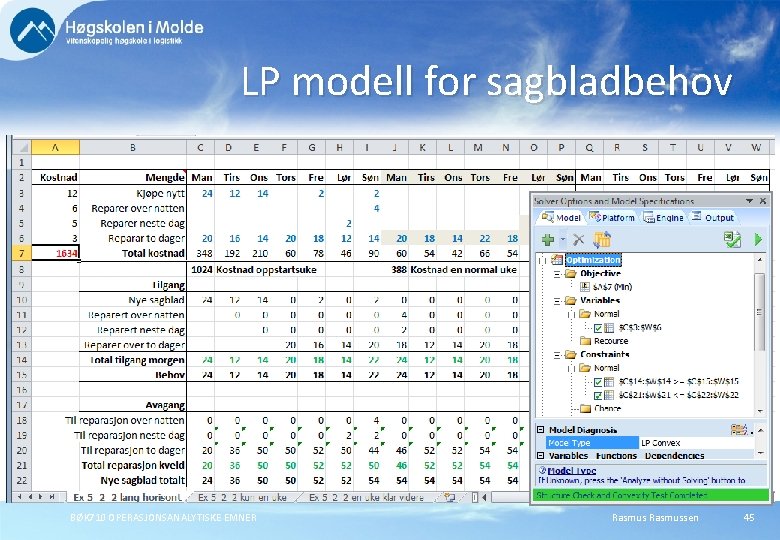
LP modell for sagbladbehov BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 45

Tidshorisont Merk at løsningen er avhengig av formuleringen. Ved kostnadsminimering vil en ende opp med minst mulig kapasitet ved enden av tidshorisonten. Av løsningen ser vi at oppstartsuken er kostbar, da må alle nyinnkjøp foretas. Vi ser også at siste uke (før nedleggelse) er svært rimelig, da lar vi være å slipe sagblad som vi ikke lenger skal bruke. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 46

Kort tidshorisont En modell for bare en uke (oppstart) vil ikke være representativ for normal drift. Om det ikke legges til restriksjoner for å sikre framtidig kapasitet, vil en måtte gjenta oppstartuken hver gang, eller legge ned etter en uke. Om en legger inn restriksjoner som sikrer kapasitet neste arbeidsdag (mandag), så vil det ikke ta fullt hensyn til de påfølgende dagene. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 47

Drift i kun en uke BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 48

En ukes drift, klargjort for neste Krever alle sagblad nyslipte BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 49

Tilordningsproblemet I tilordningsproblemer skal en f. eks. fordele hjelpemidler på oppgaver som skal løses. Hjelpemidlene/fasilitetene kan bare utføre én oppgave, og kan ikke deles. Et eksempel kan være å fordele fotballdommere på neste serierunde – hver dommer kan bare dømme en kamp. Reisekostnadene vil avhenge av hvor dommerne bor og hvor kampene spilles. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 50

Tilordningsproblemet Anta at vi har minst like mange hjelpemiddel som oppdrag/oppgaver. La j = 1, 2, . . . , n betegne hjelpemidlene La k = 1, 2, . . . , m betegne oppgavene La cjk betegne kostnaden ved å tilordne hjelpemiddel j til oppdrag k. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 51

Modell for tilordningsproblemet Minimere totale tilordningskostnader for alle hjelpemiddel og oppdrag. Max 1 oppdrag for hvert hjelpemiddel. Hvert oppdrag får tildelt ett hjelpemiddel. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 52

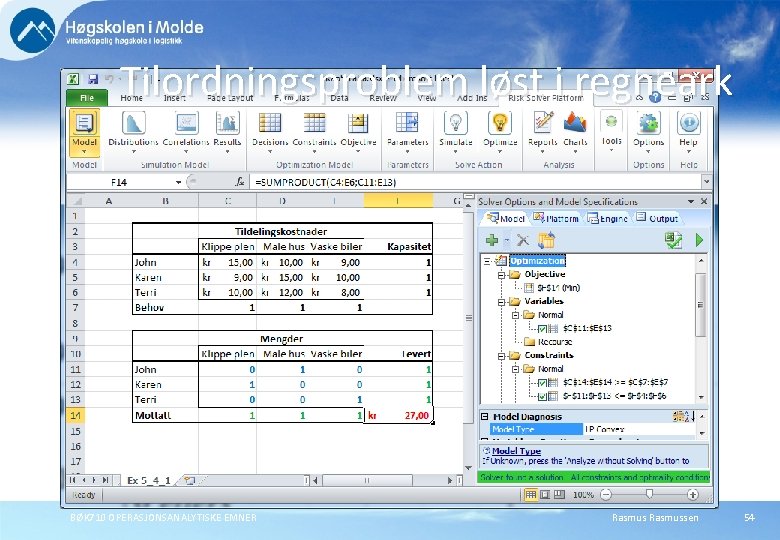
Barnearbeid hjemme Joe Klyne har tre barn som ønsker å tjene lommepenger. De har kommet med hemmelige bud på hva de mener er rettferdig betaling for følgende jobber: John Karen Terri Klippe plen 15, 9, 10, - Male hus Vaske biler 10, 9, 15, 10, 12, 8, - Faren ønsker å tildele jobbene slik at totale kostnader blir minimert. BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 53

Tilordningsproblem løst i regneark BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 54

Ubalansert tilordningsproblem Anta at vi har flere oppdrag enn hjelpemiddel. Dvs. m > n. Det betyr at vi får m - n uløste oppdrag. La: BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 55

Modell for ubalansert tilordning Minimere totale tilordningskostnader for alle hjelpemiddel og oppdrag. Max 1 oppdrag for hvert hjelpemiddel. Hvert oppdrag tildeles ett hjelpemiddel eller er udekket. Totalt udekkede oppdrag kan ikke overstige max(m – n; 0) BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 56

Generalized Assignment Problem (GAP) Anta at innenfor tidshorisonten så kan hjelpemiddel j brukes på et gitt antall oppgaver Aj. For en balansert modell må vi ha at: BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 57

GAP for ubalansert tilordning Minimere totale tilordningskostnader for alle hjelpemiddel og oppdrag. Max Aj oppdrag for hjelpemiddel j. Hvert oppdrag tildeles ett hjelpemiddel eller er udekket. Totalt udekkede oppdrag kan ikke overstige BØK 710 OPERASJONSANALYTISKE EMNER Rasmussen 58