OpenEnd Air Columns Standing Waves Review of Fundamental

Open-End Air Columns Standing Waves

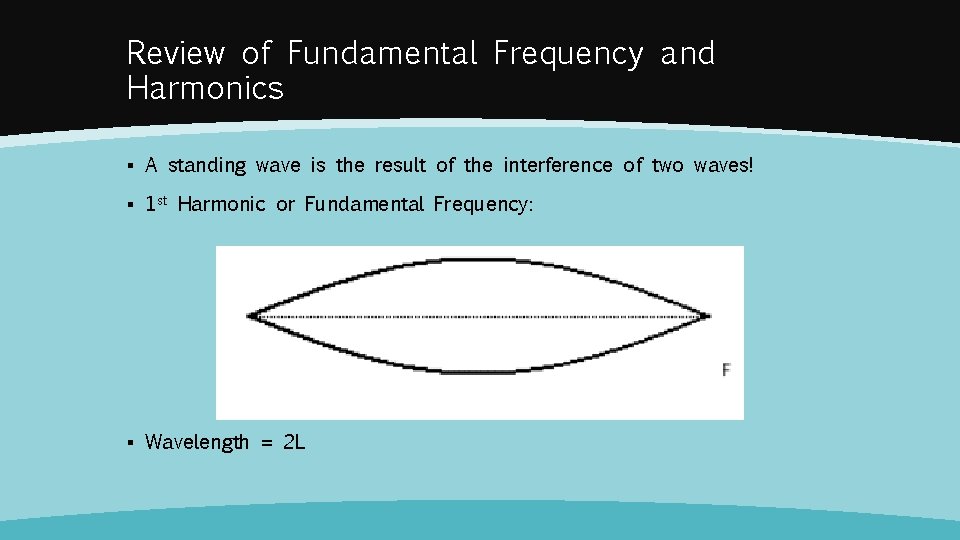
Review of Fundamental Frequency and Harmonics ▪ A standing wave is the result of the interference of two waves! ▪ 1 st Harmonic or Fundamental Frequency: ▪ Wavelength = 2 L

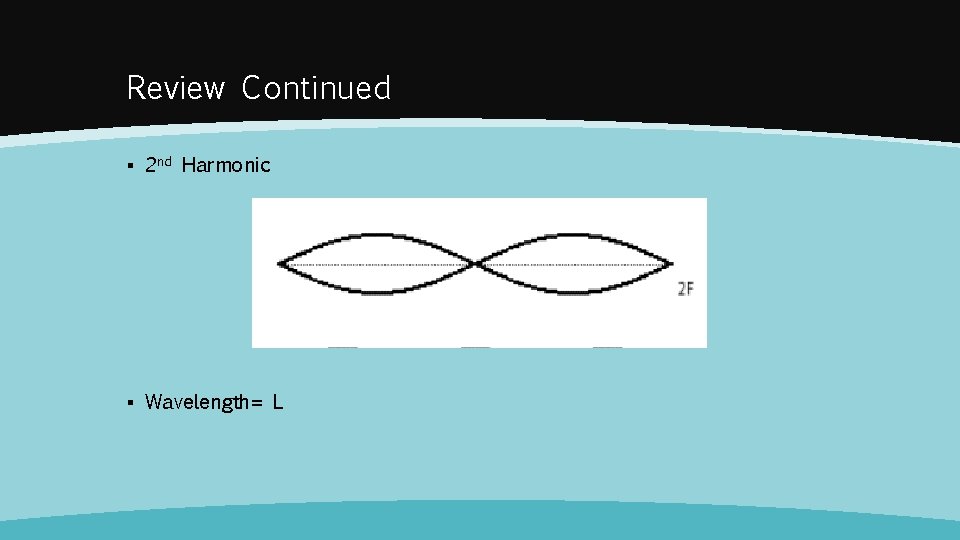
Review Continued ▪ 2 nd Harmonic ▪ Wavelength= L

Harmonics Continued ▪ 3 rd Harmonic ▪ * L = 3/2λ ▪ λ=2/3 L ▪ Where L is the string length

CHART OF HARMONICS Harmonic# # of. Wavesin String # of. Nodes Length# of. Anti-nodes Wavelength. Rel ationship 1 1/2 2 1 Wavelength = (2/1)*L 2 1 or 2/2 3 2 Wavelength = (2/2)*L 3 3/2 4 3 Wavelength = (2/3)*L 4 2 or 4/2 5 4 Wavelength = (2/4)*L 5 5/2 6 5 Wavelength = (2/5)*L

Open-End Air Columns ▪ Most instruments consist of an air column. ▪ Tone is determined by a standing wave inside the instrument. ▪ An open-end air column has two open ends like a flute. ▪ In open-end air columns there anti-nodes ALWAYS at the open ends of the instrument or column. ▪ How many waves are in this?

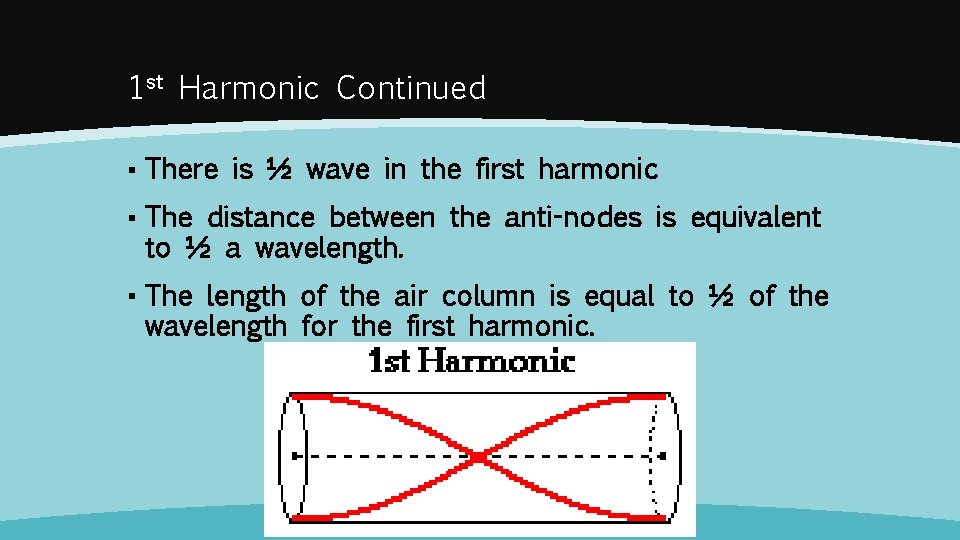
1 st Harmonic Continued ▪ There is ½ wave in the first harmonic ▪ The distance between the anti-nodes is equivalent to ½ a wavelength. ▪ The length of the air column is equal to ½ of the wavelength for the first harmonic.

2 nd Harmonic ▪ 2 nd harmonic can be produced when another node and anti-node is added, for a total of 3 antinodes and 2 nodes. ▪ There is one full wave in the column. ▪ One full wave is twice as many waves as in the first harmonic. That means that there are twice as many waves in the same amount of space. This means that the frequency is double that of the first harmonic.

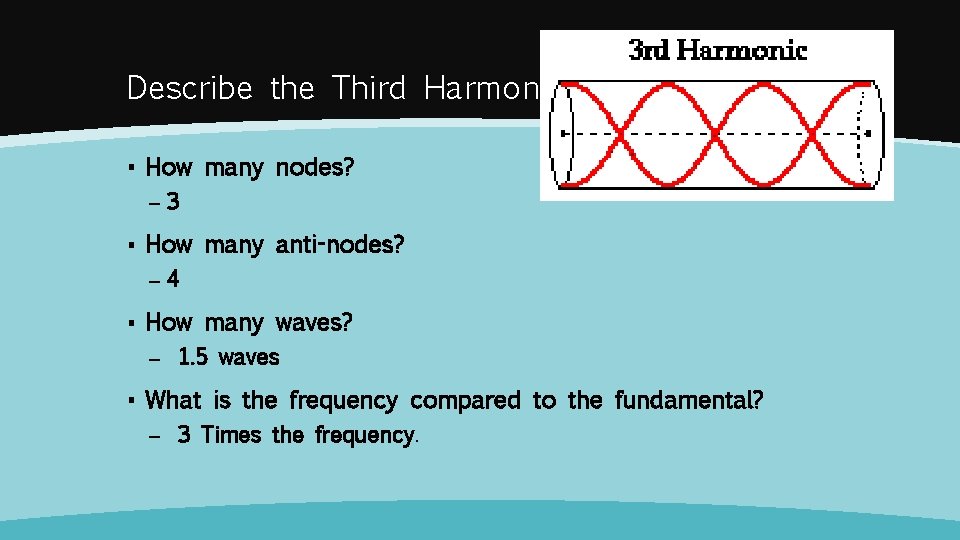
Describe the Third Harmonic ▪ How many nodes? – 3 ▪ How many anti-nodes? – 4 ▪ How many waves? – 1. 5 waves ▪ What is the frequency compared to the fundamental? – 3 Times the frequency.

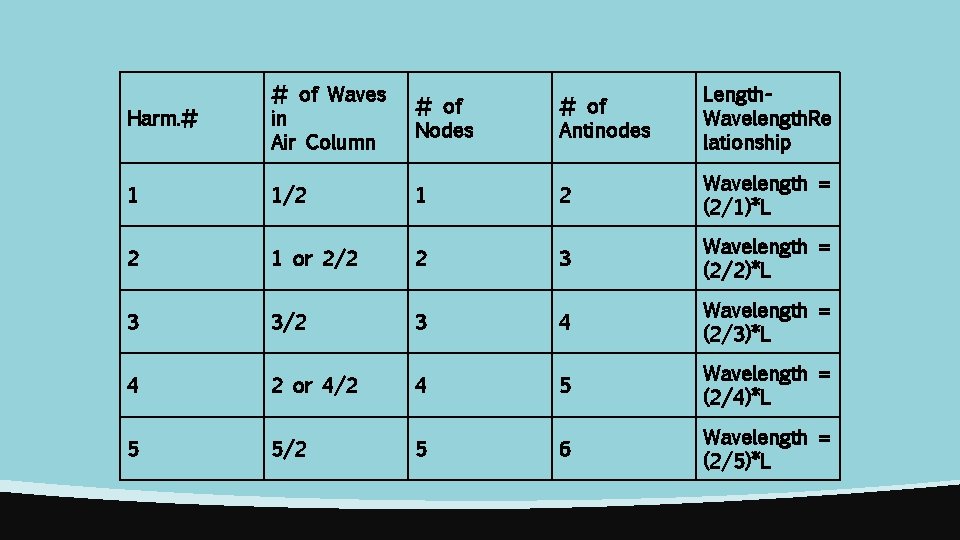
Harm. # # of Waves in Air Column # of Nodes # of Antinodes Length. Wavelength. Re lationship 1 1/2 1 2 Wavelength = (2/1)*L 2 1 or 2/2 2 3 Wavelength = (2/2)*L 3 3/2 3 4 Wavelength = (2/3)*L 4 2 or 4/2 4 5 Wavelength = (2/4)*L 5 5/2 5 6 Wavelength = (2/5)*L

Determine the length of an open-end air column required to produce a fundamental frequency (1 st harmonic) of 480 Hz. The speed of waves in air is known to be 340 m/s. speed = frequency • wavelength = speed / frequency wavelength = (340 m/s) / (480 Hz) wavelength = 0. 708 m Length = (1/2) • Wavelength Length = 0. 354 m

Example: ▪ Stan Dinghwaives is playing his open-end pipe. The frequency of the second harmonic is 880 Hz (a pitch of A 5). The speed of sound through the pipe is 350 m/sec. Find the frequency of the first harmonic and the length of the pipe. ▪ We know that the frequency will be half of the second harmonic. F=440 Hz. ▪ Λ=v/f=(350 m/s)/(440 Hz) = 0. 795 m ▪ L = 0. 5 * λ = 0. 396 m