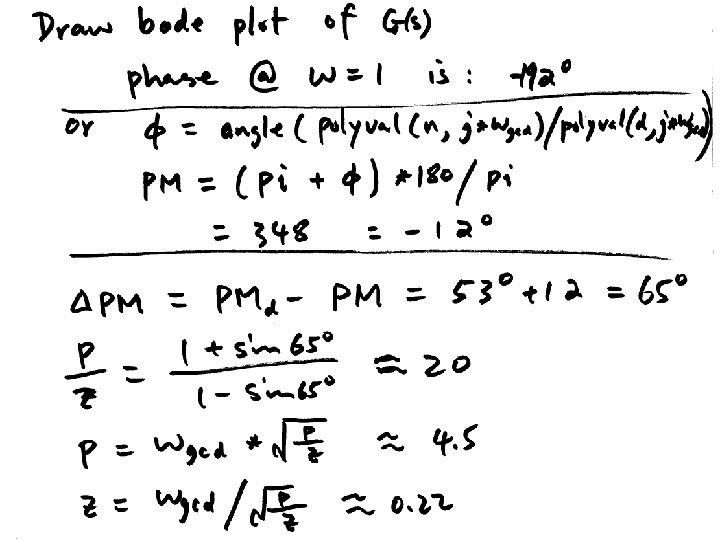Open vs Closed Loop Frequency Response And Frequency











![clear all; n=[0 0 40]; d=[1 2 0]; figure(1); clf; margin(n, d); %proportional control clear all; n=[0 0 40]; d=[1 2 0]; figure(1); clf; margin(n, d); %proportional control](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-17.jpg)



![n=[0 0 1]; d=[0. 02 0. 3 1 0]; figure(1); clf; margin(n, d); Could n=[0 0 1]; d=[0. 02 0. 3 1 0]; figure(1); clf; margin(n, d); Could](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-21.jpg)

![n=[0 0 5]; d=[0. 02 0. 3 1 0]; figure(1); clf; margin(n, d); Mp n=[0 0 5]; d=[0. 02 0. 3 1 0]; figure(1); clf; margin(n, d); Mp](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-23.jpg)









![Lead design example • Plant transfer function is given by: • n=[50000]; d=[1 60 Lead design example • Plant transfer function is given by: • n=[50000]; d=[1 60](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-33.jpg)
![n=[50000]; d=[1 60 500 0]; G=tf(n, d); figure(1); margin(G); Mp_d = 16/100; zeta_d =0. n=[50000]; d=[1 60 500 0]; G=tf(n, d); figure(1); margin(G); Mp_d = 16/100; zeta_d =0.](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-34.jpg)



![n=[50]; d=[1/5 1 0]; figure(1); clf; margin(n, d); grid; hold on; Mp = 20/100; n=[50]; d=[1/5 1 0]; figure(1); clf; margin(n, d); grid; hold on; Mp = 20/100;](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-38.jpg)





![n=[50]; d=[1/5 1 0]; figure(1); clf; margin(n, d); grid; hold on; Mp = 20/100; n=[50]; d=[1/5 1 0]; figure(1); clf; margin(n, d); grid; hold on; Mp = 20/100;](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-45.jpg)







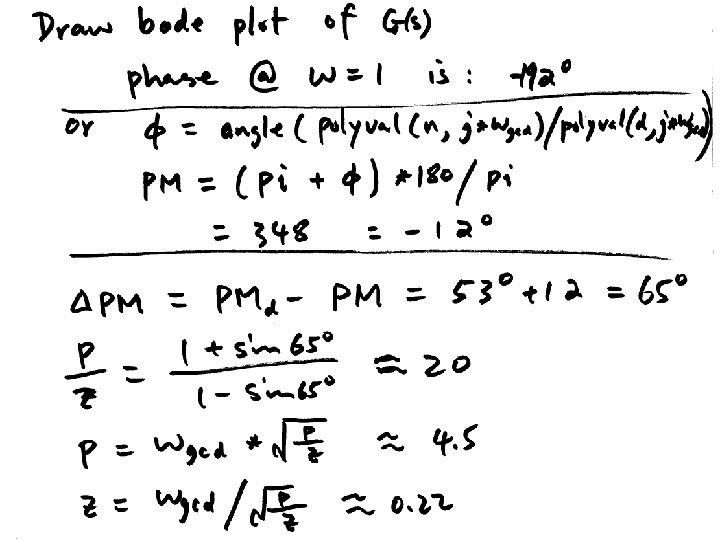









- Slides: 63

Open vs Closed Loop Frequency Response And Frequency Domain Specifications C(s) Goal: 1) Define typical “good” freq resp shape for closed-loop 2) Relate closed-loop freq response shape to step response shape 3) Relate closed-loop freq shape to open-loop freq resp shape 4) Design C(s) to make C(s)G(s) into “good” shape.

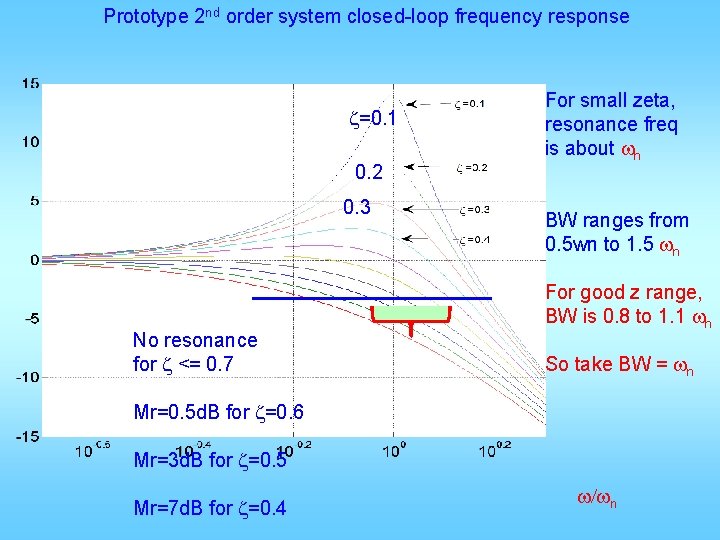
Prototype 2 nd order system closed-loop frequency response z=0. 1 0. 2 0. 3 No resonance for z <= 0. 7 For small zeta, resonance freq is about wn BW ranges from 0. 5 wn to 1. 5 wn For good z range, BW is 0. 8 to 1. 1 wn So take BW = wn Mr=0. 5 d. B for z=0. 6 Mr=3 d. B for z=0. 5 Mr=7 d. B for z=0. 4 w/wn

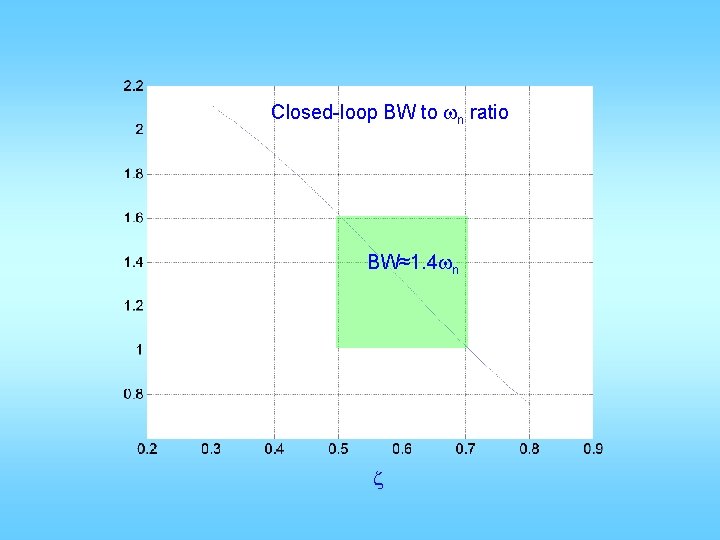
Closed-loop BW to wn ratio BW≈1. 4 wn z

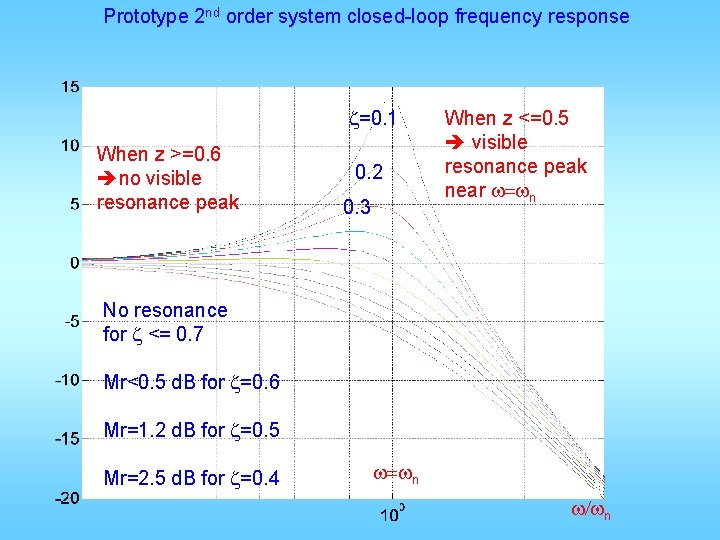
Prototype 2 nd order system closed-loop frequency response z=0. 1 When z >=0. 6 no visible resonance peak 0. 2 0. 3 When z <=0. 5 visible resonance peak near w=wn No resonance for z <= 0. 7 Mr<0. 5 d. B for z=0. 6 Mr=1. 2 d. B for z=0. 5 Mr=2. 5 d. B for z=0. 4 w=wn w/wn

Prototype 2 nd order system closed-loop frequency response Mr vs z

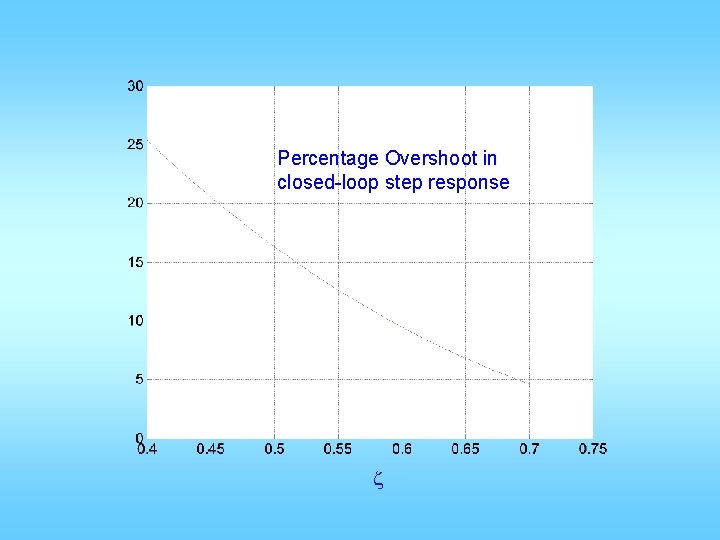
Percentage Overshoot in closed-loop step response z

Percentage Overshoot in closed-loop step response Mr

Percentage Overshoot in closed-loop step response Mr in d. B

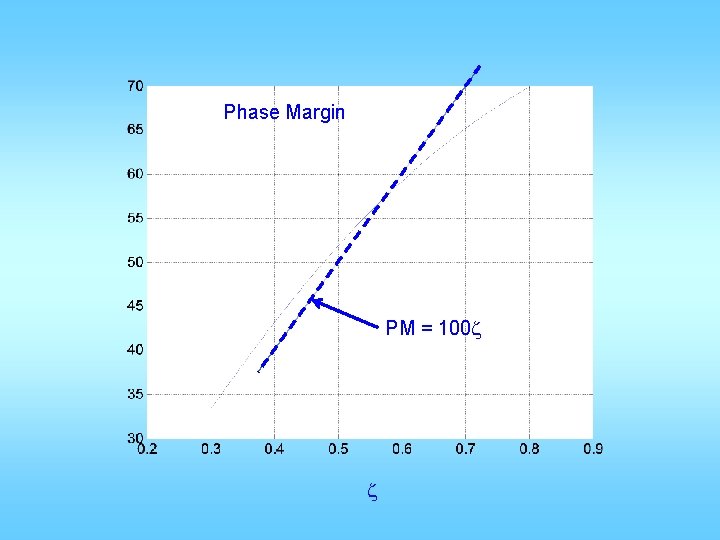
Phase Margin PM = 100 z z

PM+Mp =70 line Percentage Overshoot in closed-loop step response Phase Margin in degrees

z=0. 1 0. 2 0. 3 0. 4 wgc In the range of good zeta, wgc is about 0. 65 times to 0. 8 times wn w/wn

Open-loop wgc to wn ratio wgc≈0. 7 wn z

z=0. 1 In the range of good zeta, PM is about 100*z 0. 2 0. 3 0. 4 w/wn

Important relationships • Closed-loop BW are very close to wn • Open-loop gain cross over wgc ≈ (0. 65~0. 8)* wn, • When z <= 0. 6, wr and wn are close • When z >= 0. 7, no resonance • z determines phase margin and Mp: z 0. 4 0. 5 0. 6 0. 7 PM Mp 44 25 53 16 61 10 67 5 deg % ≈100 z

Desired Bode plot shape

Proportional controller design • Obtain open loop Bode plot • Convert design specs into Bode plot req. • Select KP based on requirements: – For improving ess: KP = Kp, v, a, des / Kp, v, a, act – For fixing Mp: select wgcd to be the freq at which PM is sufficient, and KP = 1/|G(jwgcd)| – For fixing speed: from td, tr, tp, or ts requirement, find out wn, let wgcd = wn and choose KP as above
![clear all n0 0 40 d1 2 0 figure1 clf marginn d proportional control clear all; n=[0 0 40]; d=[1 2 0]; figure(1); clf; margin(n, d); %proportional control](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-17.jpg)
clear all; n=[0 0 40]; d=[1 2 0]; figure(1); clf; margin(n, d); %proportional control design: figure(1); hold on; grid; V=axis; Mp = 10/100; zeta = sqrt((log(Mp))^2/(pi^2+(log(Mp))^2)); PMd = zeta * 100 + 3; semilogx(V(1: 2), [PMd-180], ': r'); %get desired w_gc x=ginput(1); w_gcd = x(1); KP = 1/abs(polyval(n, j*w_gcd)/polyval(d, j*w_gcd)); figure(2); margin(KP*n, d); figure(3); stepchar(KP*n, d+KP*n);

PD Controller

KP/KD 20*log(KP) Place wgcd here

![n0 0 1 d0 02 0 3 1 0 figure1 clf marginn d Could n=[0 0 1]; d=[0. 02 0. 3 1 0]; figure(1); clf; margin(n, d); Could](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-21.jpg)
n=[0 0 1]; d=[0. 02 0. 3 1 0]; figure(1); clf; margin(n, d); Could be a little less Mp = 10/100; zeta = sqrt((log(Mp))^2/(pi^2+(log(Mp))^2)); PMd = zeta * 100 + 3; tr = 0. 3; w_n=1. 8/tr; w_gcd = w_n; PM = angle(polyval(n, j*w_gcd)/polyval(d, j*w_gcd)); phi = PMd*pi/180 -PM; Td = tan(phi)/w_gcd; KP = 1/abs(polyval(n, j*w_gcd)/polyval(d, j*w_gcd)); KP = KP/sqrt(1+Td^2*w_gcd^2); KD=KP*Td; ngc = conv(n, [KD KP]); figure(2); margin(ngc, d); figure(3); stepchar(ngc, d+ngc);

Variation • Restricted to using KP = 1 • Meet Mp requirement • Find wgc and PM • Find PMd • Let f = PMd – PM + (a few degrees) • Compute TD = tan(f)/wgcd • KP = 1; KD=KPTD
![n0 0 5 d0 02 0 3 1 0 figure1 clf marginn d Mp n=[0 0 5]; d=[0. 02 0. 3 1 0]; figure(1); clf; margin(n, d); Mp](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-23.jpg)
n=[0 0 5]; d=[0. 02 0. 3 1 0]; figure(1); clf; margin(n, d); Mp = 10/100; zeta = sqrt((log(Mp))^2/(pi^2+(log(Mp))^2)); PMd = zeta * 100 + 18; [GM, PM, wgc, wpc]=margin(n, d); phi = (PMd-PM)*pi/180; Td = tan(phi)/wgc; Kp=1; Kd=Kp*Td; ngc = conv(n, [Kd Kp]); figure(2); margin(ngc, d); figure(3); stepchar(ngc, d+ngc);






Lead Controller Design

plead zlead 20 log(Kzlead/plead) Goal: select z and p so that max phase lead is at desired wgc and max phase lead = PM defficiency!


Lead Design • • • From specs => PMd and wgcd From plant, draw Bode plot Find PMhave = 180 + angle(G(jwgcd) DPM = PMd - PMhave + a few degrees Choose a=plead/zlead so that fmax = DPM and it happens at wgcd
![Lead design example Plant transfer function is given by n50000 d1 60 Lead design example • Plant transfer function is given by: • n=[50000]; d=[1 60](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-33.jpg)
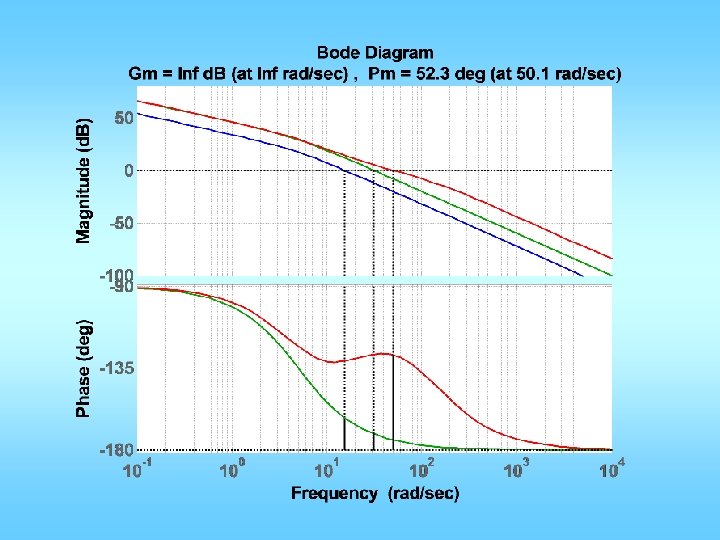
Lead design example • Plant transfer function is given by: • n=[50000]; d=[1 60 500 0]; • Desired design specifications are: – Step response overshoot <= 16% – Closed-loop system BW>=20;
![n50000 d1 60 500 0 Gtfn d figure1 marginG Mpd 16100 zetad 0 n=[50000]; d=[1 60 500 0]; G=tf(n, d); figure(1); margin(G); Mp_d = 16/100; zeta_d =0.](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-34.jpg)
n=[50000]; d=[1 60 500 0]; G=tf(n, d); figure(1); margin(G); Mp_d = 16/100; zeta_d =0. 5; % or calculate from Mp_d PMd = 100*zeta_d + 3; BW_d=20; w_gcd = BW_d*0. 7; Gwgc=evalfr(G, j*w_gcd); PM = pi+angle(Gwgc); phimax= PMd*pi/180 -PM; alpha=(1+sin(phimax))/(1 -sin(phimax)); zlead= w_gcd/sqrt(alpha); plead=w_gcd*sqrt(alpha); K=sqrt(alpha)/abs(Gwgc); ngc = conv(n, K*[1 zlead]); dgc = conv(d, [1 plead]); figure(1); hold on; margin(ngc, dgc); hold off; [ncl, dcl]=feedback(ngc, dgc, 1, 1); figure(2); step(ncl, dcl);

Before design After design

Closed-loop Bode plot by: margin(ncl*1. 414, dcl); Magnitude plot shifted up 3 So, gc is BW

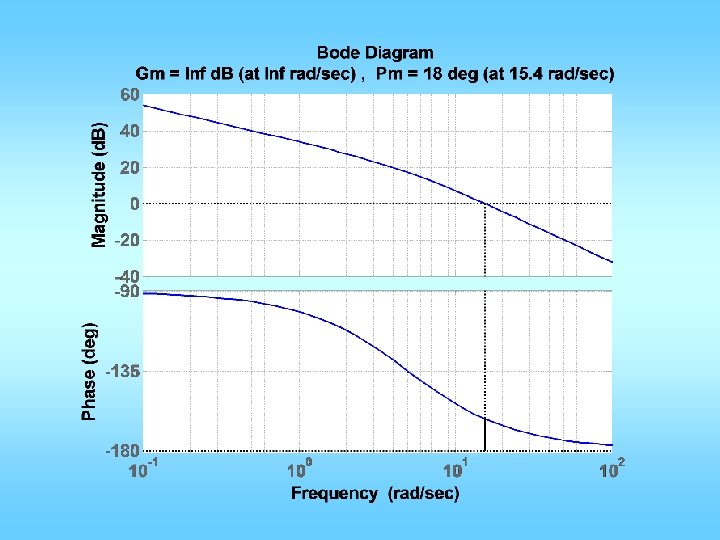
![n50 d15 1 0 figure1 clf marginn d grid hold on Mp 20100 n=[50]; d=[1/5 1 0]; figure(1); clf; margin(n, d); grid; hold on; Mp = 20/100;](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-38.jpg)
n=[50]; d=[1/5 1 0]; figure(1); clf; margin(n, d); grid; hold on; Mp = 20/100; zeta = sqrt((log(Mp))^2/(pi^2+(log(Mp))^2)); PMd = zeta * 100 + 10; ess 2 ramp= 1/200; Kvd=1/ess 2 ramp; Kva = n(end)/d(end-1); Kzp = Kvd/Kva; figure(2); margin(Kzp*n, d); grid; [GM, PM, wpc, wgc]=margin(Kzp*n, d); w_gcd=wgc; phimax = (PMd-PM)*pi/180; alpha=(1+sin(phimax))/(1 -sin(phimax)); z=w_gcd/sqrt(alpha); p=w_gcd*sqrt(alpha); ngc = conv(n, alpha*Kzp*[1 z]); dgc = conv(d, [1 p]); figure(3); margin(tf(ngc, dgc)); grid; [ncl, dcl]=feedback(ngc, dgc, 1, 1); figure(4); step(ncl, dcl); grid; figure(5); margin(ncl*1. 414, dcl); grid;






![n50 d15 1 0 figure1 clf marginn d grid hold on Mp 20100 n=[50]; d=[1/5 1 0]; figure(1); clf; margin(n, d); grid; hold on; Mp = 20/100;](https://slidetodoc.com/presentation_image_h2/48d57e3da07d246444e05d4d5dcce5c5/image-45.jpg)
n=[50]; d=[1/5 1 0]; figure(1); clf; margin(n, d); grid; hold on; Mp = 20/100; zeta = sqrt((log(Mp))^2/(pi^2+(log(Mp))^2)); PMd = zeta * 100 + 10; ess 2 ramp= 1/200; Kvd=1/ess 2 ramp; Kva = n(end)/d(end-1); Kzp = Kvd/Kva; figure(2); margin(Kzp*n, d); grid; [GM, PM, wpc, wgc]=margin(Kzp*n, d); w_gcd=wgc; phimax = (PMd-PM)*pi/180; alpha=(1+sin(phimax))/(1 -sin(phimax)); z=w_gcd/alpha^. 25; %sqrt(alpha); p=w_gcd*alpha^. 75; %sqrt(alpha); ngc = conv(n, alpha*Kzp*[1 z]); dgc = conv(d, [1 p]); figure(3); margin(tf(ngc, dgc)); grid; [ncl, dcl]=feedback(ngc, dgc, 1, 1); figure(4); step(ncl, dcl); grid; figure(5); margin(ncl*1. 414, dcl); grid;