Open Seminar at Tokyo Polytechnic University POD AND

Open Seminar at Tokyo Polytechnic University POD AND NEW INSIGHTS IN WIND ENGINEERING LE THAI HOA Vietnam National University, Hanoi PART 2

CONTENTS Introduction POD and its Proper Transformations in Time Domain and Frequency Domain New Insights in Wind Engineering Topic 1: POD and Pressure Fields Topic 2: POD and Wind Fields, Wind Simulation Topic 3: POD and Response Prediction Topic 4: POD and System Identification Further Perspectives and Development

TOPIC 3 STOCHASTIC RESPONSE PREDICTION OF WND-EXCITED STRUCTURES IN FREQUENCY DOMAIN AND TIME DOMAIN l l l Introduction Response Prediction in Frequency Domain Response Prediction in Time Domain Numerical Examples Remarks and Insights

Introduction (1) q Gust response prediction of structures due to turbulent wind faces the difficulty in projecting the full-scale buffeting forces on the structural generalized coordinates. The joint acceptance function technique has been used for this purpose the conventional approach. q Proper Orthogonal Decomposition (POD) and its Proper Transformations decompose the full-scale buffeting forces into so-called turbulent loading modes and projects onto generalized coordinates and structural modes.

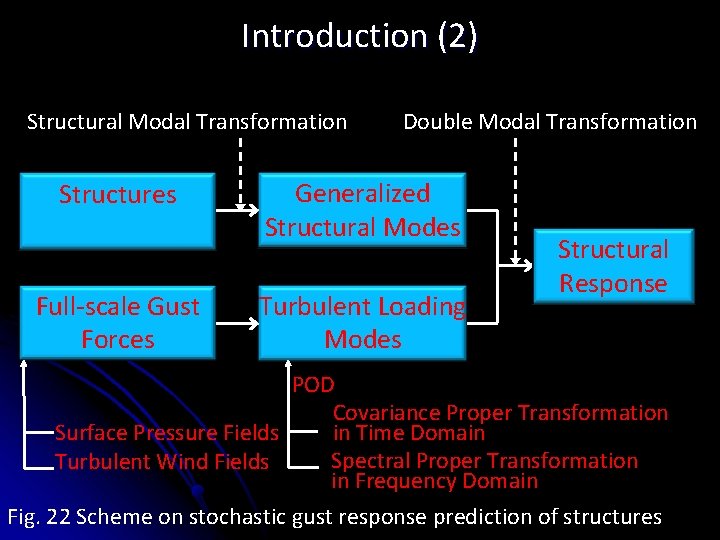
Introduction (2) Structural Modal Transformation Structures Full-scale Gust Forces Double Modal Transformation Generalized Structural Modes Turbulent Loading Modes Structural Response POD Covariance Proper Transformation Surface Pressure Fields in Time Domain Spectral Proper Transformation Turbulent Wind Fields in Frequency Domain Fig. 22 Scheme on stochastic gust response prediction of structures

Introduction (3) q Gust response of structures firstly proposed in the frequency domain by Davenport 1962. Time domain gust response was üdeveloped Formulation of the stochastic gust response prediction by Chen 1996 of structures applies both the POD-based Proper q Double Modal Transformation (DMT) for gust response Transformations prediction in the frequency domain proposed by Carassale and üSolari Effects of number of for andsimple low-order 1999, application frameturbulent structuresloading and modes on and. Solari global responses of for that of buildings by generalized Carassale 1999, 2000; Chen 2005; bridges by Solari 2005 using Spectral Proper Transformation. structures Interaction between structuralinmodes and thedomain, qüStochastic gust responsethe is predicted the frequency turbulent loading modes thus the time-domain formulation have been required as new line of the POD. Therefore, problems of unsteady forces, nonlinear aerodynamics can be solved as further development

Stochastic Gust Response in Time Domain q 1 DOF motion equation in i-th generalized coordinate: q Turbulent fields u(t), w(t) are approximated as the CPT: q 1 DOF equation in the generalized coordinate is expressed: q : Cross modal coefficients Time histories of generalized responses obtained by using direct integration methods (here Newton-beta method used). Finally, the global responses are determined

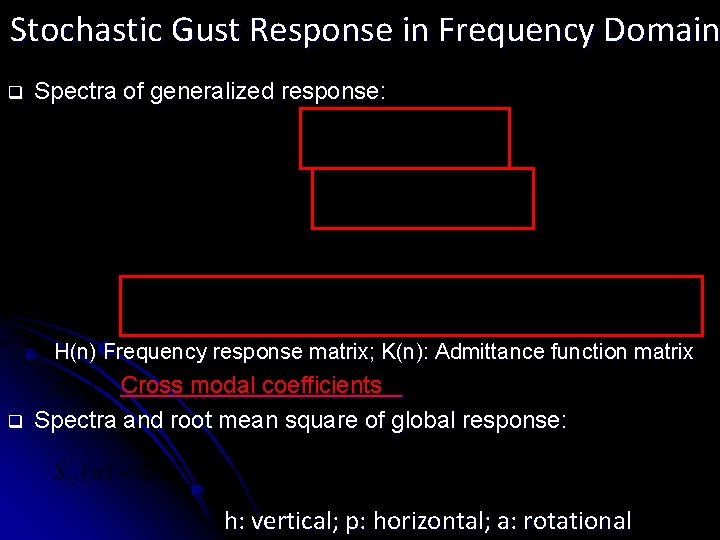
Stochastic Gust Response in Frequency Domain q Spectra of generalized response: H(n) Frequency response matrix; K(n): Admittance function matrix q Cross modal coefficients Spectra and root mean square of global response: h: vertical; p: horizontal; a: rotational

Numerical Example q q q A line-like structure is used for demonstration and investigation Kaimal spectrum and Bush&Panofsky spectrum are used auto spectral densities of longitudinal and vertical turbulences, respectively. Davenport’s empirical formula is used for spanwise coherence. Liepmann’s empirical function is used for the aerodynamic admittance. Static aerodynamic coefficients and its first-derivatives as

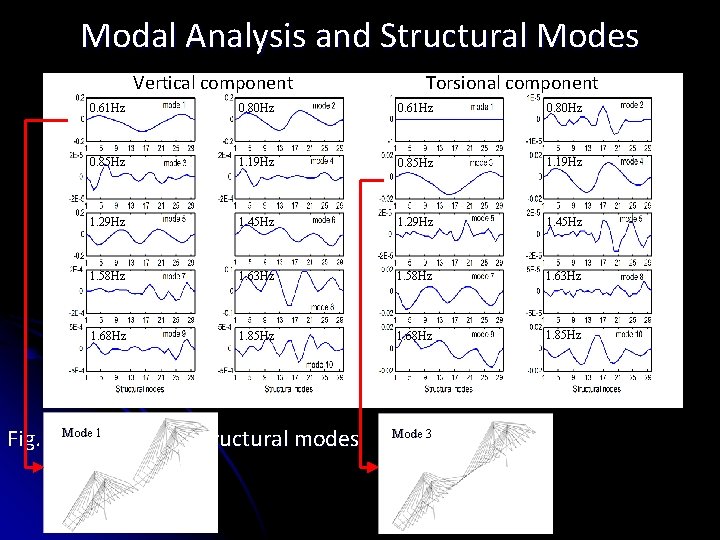
Modal Analysis and Structural Modes Vertical component Torsional component 0. 61 Hz 0. 80 Hz 0. 85 Hz 1. 19 Hz 1. 29 Hz 1. 45 Hz 1. 58 Hz 1. 63 Hz 1. 68 Hz 1. 85 Hz 1 Fig. 23 Mode Normalized structural modes Mode 3

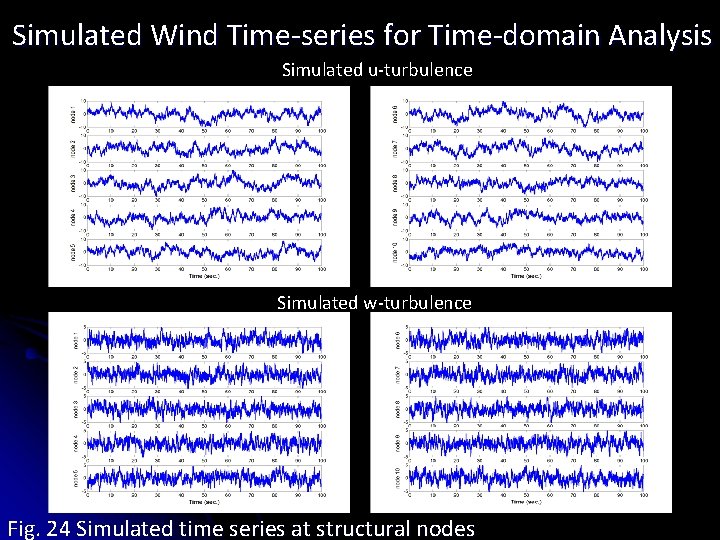
Simulated Wind Time-series for Time-domain Analysis Simulated u-turbulence Simulated w-turbulence Fig. 24 Simulated time series at structural nodes

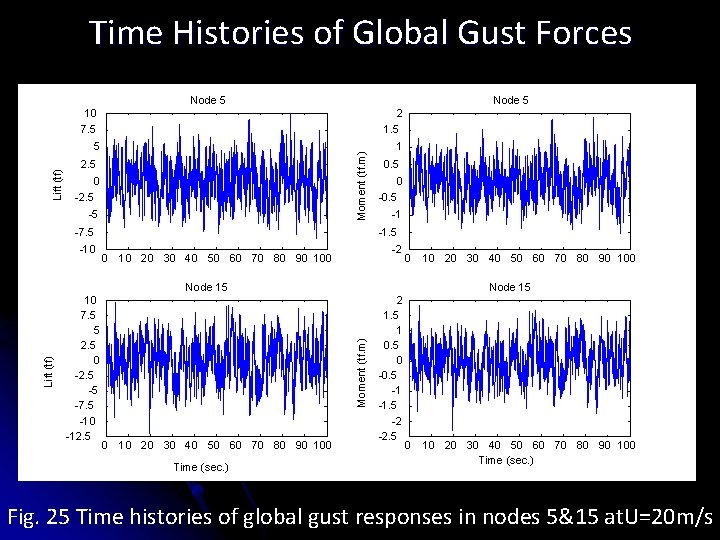
Time Histories of Global Gust Forces Node 5 10 7. 5 2 1. 5 5 1 Moment (tf. m) Lift (tf) Node 5 2. 5 0 -2. 5 -5 -7. 5 -10 0. 5 0 -0. 5 -1 -1. 5 0 -2 10 20 30 40 50 60 70 80 90 100 0 Node 15 Moment (tf. m) Lift (tf) Node 15 10 7. 5 5 2. 5 0 -2. 5 -5 -7. 5 -10 -12. 5 0 10 20 30 40 50 60 70 80 90 100 Time (sec. ) 10 20 30 40 50 60 70 80 90 100 2 1. 5 1 0. 5 0 -0. 5 -1 -1. 5 -2 -2. 5 0 10 20 30 40 50 60 70 80 90 100 Time (sec. ) Fig. 25 Time histories of global gust responses in nodes 5&15 at. U=20 m/s

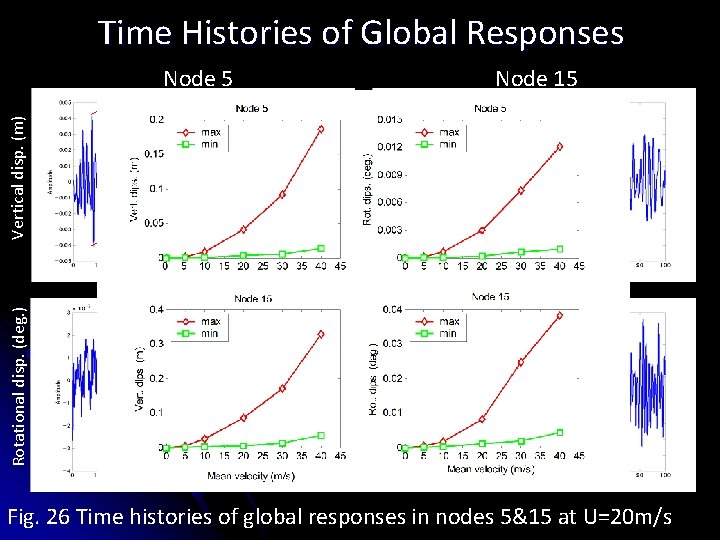
Time Histories of Global Responses Rotational disp. (deg. ) Vertical disp. (m) Node 5 Node 15 2 x Max. amplitude 2 x Max. Amplitude Fig. 26 Time histories of global responses in nodes 5&15 at U=20 m/s

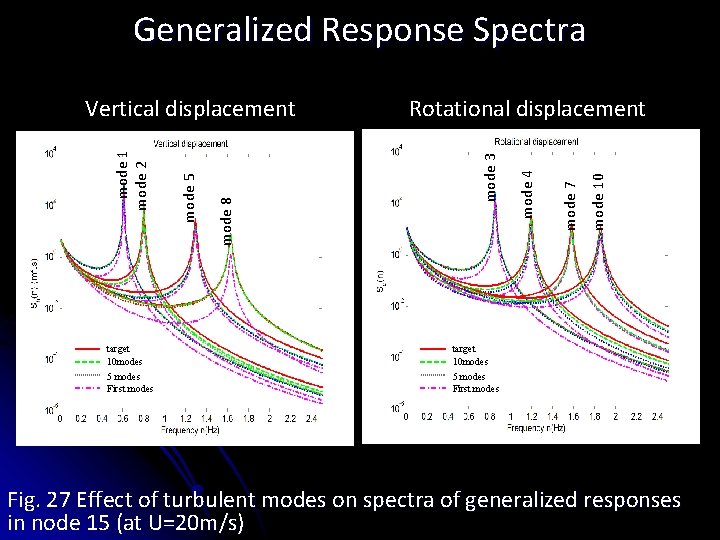
Generalized Response Spectra target 10 modes 5 modes First modes mode 10 mode 7 mode 4 Rotational displacement mode 3 mode 8 mode 5 mode 1 mode 2 Vertical displacement target 10 modes 5 modes First modes Fig. 27 Effect of turbulent modes on spectra of generalized responses in node 15 (at U=20 m/s)

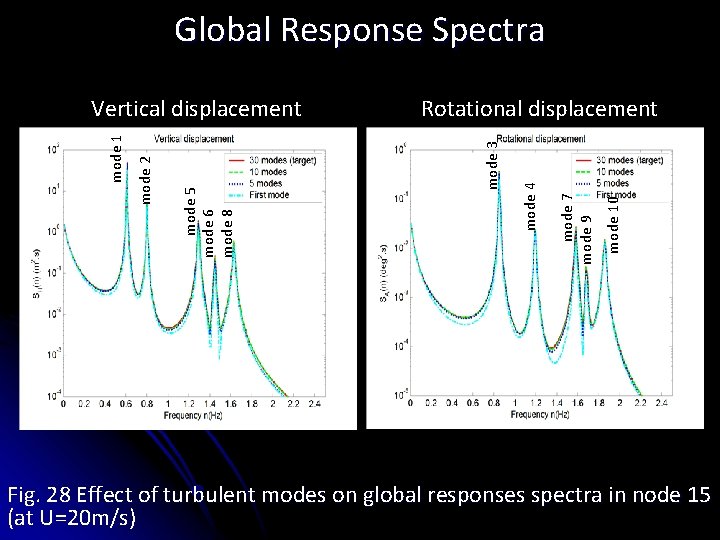
Global Response Spectra mode 10 mode 7 mode 9 mode 4 Rotational displacement mode 3 mode 5 mode 6 mode 8 mode 2 mode 1 Vertical displacement Fig. 28 Effect of turbulent modes on global responses spectra in node 15 (at U=20 m/s)

Cross Modal Coefficients Lift Moment Interaction between u-turbulent spectral modes and structural modes Fig. 29 Influence of spectral mode on structural modes Moment Lift Between w-turbulent spectral modes and structural modes

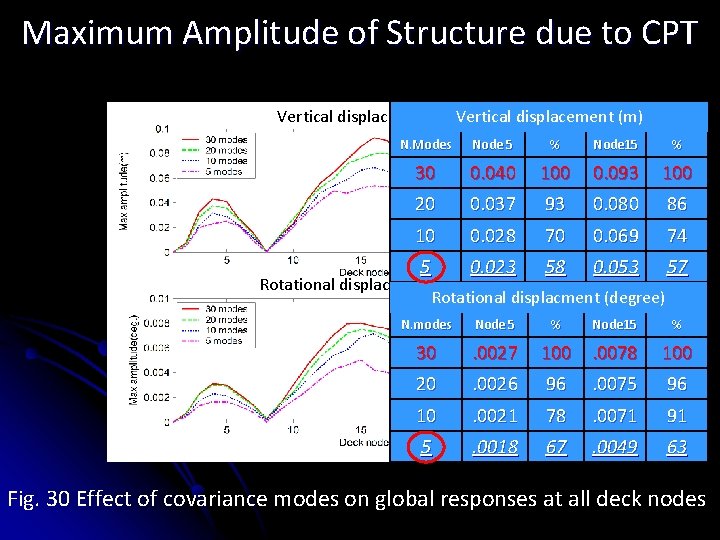
Maximum Amplitude of Structure due to CPT Vertical displacement (m) N. Modes Node 5 % Node 15 % 30 0. 040 100 0. 093 100 20 0. 037 93 0. 080 86 10 0. 028 70 0. 069 74 5 0. 023 58 0. 053 57 N. modes Node 5 % Node 15 % 30 . 0027 100. 0078 100 20 . 0026 96 . 0075 96 10 . 0021 78 . 0071 91 5 . 0018 67 . 0049 63 Rotational displacement (degree) Rotational displacment (degree) Fig. 30 Effect of covariance modes on global responses at all deck nodes

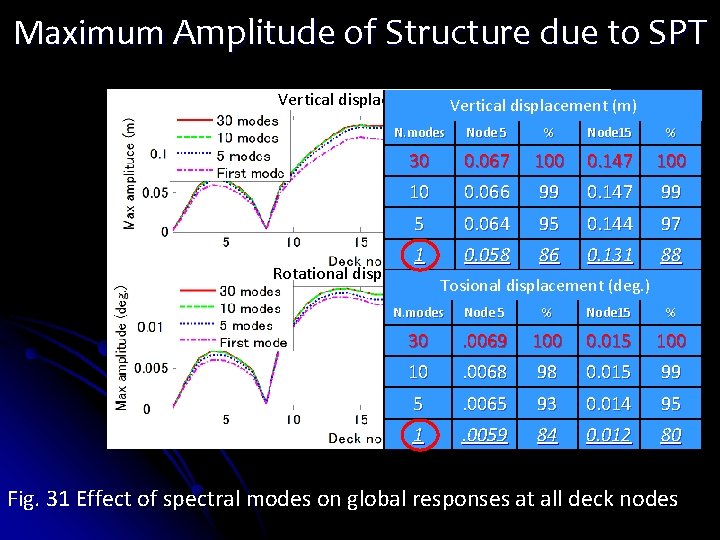
Maximum Amplitude of Structure due to SPT Vertical displacement (m) N. modes Node 5 % Node 15 % 30 0. 067 100 0. 147 100 10 0. 066 99 0. 147 99 5 0. 064 95 0. 144 97 1 0. 058 86 0. 131 88 N. modes Node 5 % Node 15 % 30 . 0069 100 0. 015 100 10 . 0068 98 0. 015 99 5 . 0065 93 0. 014 95 1 . 0059 84 0. 012 80 Rotational displacement (degree) Tosional displacement (deg. ) Fig. 31 Effect of spectral modes on global responses at all deck nodes

Remarks and Insights Framework on the gust response of bridges is formulated in both the time domain and frequency domain using both PODbased Proper Transformations with comprehensive approach of spatially-correlated turbulent field. q Only few basic. Gust turbulent modes contributeofdominantly Thus, Unsteady Response Prediction structures and effectively onto thethe global of bridges. formulated thanks SPT gust and response CPT in both frequency Concretely, thetime firstdomain spectral using turbulent mode. Response contributes domain and the Impulse significantly on will the gust response, whereas more basic Functions Model be next development covariance modes are required for the gust response. q q Effective turbulent field and cross modal coefficients can be refined for simulating the turbulent field and estimating the gust response by using few turbulent modes and effective spectral band.

TOPIC 4 SYSTEM IDENTIFICATION OF WNDEXCITED STRUCTURES IN FREQUENCY DOMAIN AND TIME DOMAIN l l l Introduction Frequency Domain Decomposition (FDD) Stochastic Subspace Identification (SSI) Numerical Examples Remarks and Insights

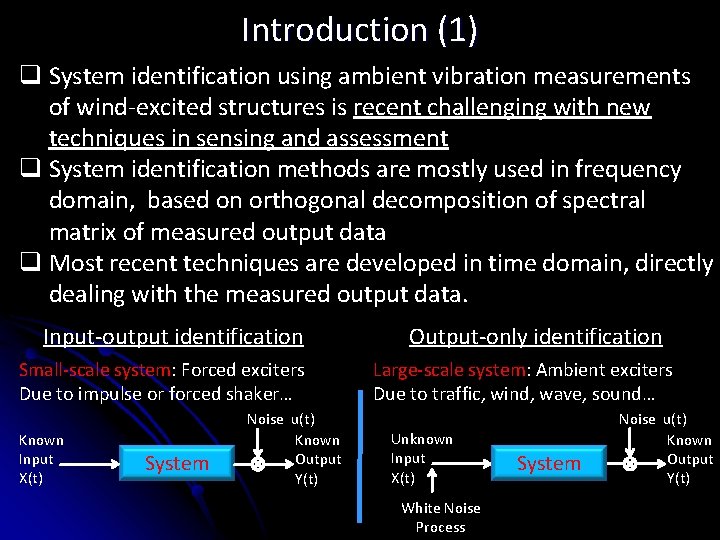
Introduction (1) q System identification using ambient vibration measurements of wind-excited structures is recent challenging with new techniques in sensing and assessment q System identification methods are mostly used in frequency domain, based on orthogonal decomposition of spectral matrix of measured output data q Most recent techniques are developed in time domain, directly dealing with the measured output data. Input-output identification Small-scale system: Forced exciters Due to impulse or forced shaker… Known Input X(t) System Noise u(t) Known Output Y(t) Output-only identification Large-scale system: Ambient exciters Due to traffic, wind, wave, sound… Unknown Input X(t) White Noise Process System Noise u(t) Known Output Y(t)

Introduction (2) Output-only System Identification Stochastic Subspace Identification (SSI) Nonparametric Methods Parametric Methods ü Projection and decomposition of either or covariance in Frequency Domain inspectral Time Domain P. Overschee matrices of output response time series, even dealing with B. D Moor, 1996 Peak Picking SSI with AR, ARMA directly output data must be needed Technique (PPT) J. H. Weng et. al. , 2008 ü Some robustness numerical methods are used such as QR Frequency Domain SSI with Covariance Decomposition (FDD) Decomposition, Least Squares, Singular Value Decomposition… Enhanced Frequency J. S. Bandat ü Advantage of POD will be exploited for this SSIpurpose with Data of Domain Decomposition et al. , 1993 R. Brincker decomposition Covariance Matrix et al. , 2001 Spectral Matrix of Output Data A. Yoshida Y. Tamura, 2004 L. Carassale, F. Percivale, 2007 Fig. 32 Only-output system identification methods of Output Data Hankel Matrix of Output Data

Comparison between FDD and SSI FDD SSI § Formulated in the frequency domain § Based on spectral matrix of measured output data § Formulated in the time domain § Directly deal with measured output data or covariance matrix § High accurate identification in cases of high noises § High applicable for closed modal identification § More complicated § Prior knowledge of modal frequencies not is required § Less accurate identification in cases of high noises § High applicable for closed modal identification § Easier in identification § Prior knowledge of modal frequencies is required

Frequency Domain Decomposition (FFD) q Firstly, cross spectral matrix estimated from measured output data üQRDecomposition üLeast Squares üSingular Values Decomposition… q Secondly, cross spectral matrix is decomposed using POD then Where: Eigenvalue and eigenvector matrices In the FDD, prior knowledge of modal frequencies is generally required to identify the modal parameters q ith modal identification, we decompose at selected frequency then and Thus, the ith mode:

State-space Representation in SSI (1) q Continuous state-space representation: Where: Stochastic identification requires finding system parameters: A, C, modal parameters, frequencies and damping ratios from ambient output x(t): measurements state vector; yk(t) : state matrix; input matrix; output matrix q Discrete state-space representation at interval time Inputs Where: Input-output relationship: If inputs are white noises (during free vibration), model reduce: Broad-band white noises

SSI-DATA (2) q Reconstructing output data to Hankel matrices (past, futurestates) q Orthogonal projection of Hankel matrices, the decomposing the projection using the POD üQRDecomposition üLeast Squares then q Identifying the system matrices: A, C and üSingular Values Decomposition… Where: from without last l row; from without first l rows of Extended observability matrix q Identifying modal parameter: then

Refining FDD, SSI by Wavelet Analysis q System identification techniques of structures from ambient natural excitations usually has many difficulties associated with high noises, low and closed eigenvalues (frequencies), a lot of effects on measured output data q Idea of the time-frequency analysis (wavelet analysis) can be applicable for to system identification or refinement of FDD, SSI, because of some following reasons: ü Wavelet analysis reveals time information of sources of excitation and eigenvalues ocurrance ü Wavelet analysis eliminates and localizes the system noise ü Wavelet analysis decomposes and localizes at many frequency bands ü Especially, wavelet analysis does high resolution on low frequency bands that clearly separate low and closed eigenvalues

Field Measurements of 5 -storey Steel Frame Floor 5 Floor 4 Floor 3 Floor 2 Floor 1 Ground Fig. 33 5 -storey steel frame at test site Disaster Prevention Research Institute (DPRI), Kyoto University

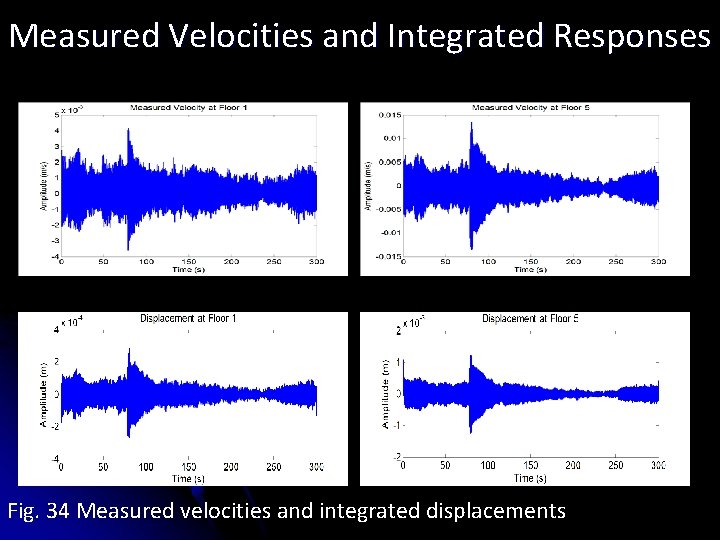
Measured Velocities and Integrated Responses Fig. 34 Measured velocities and integrated displacements

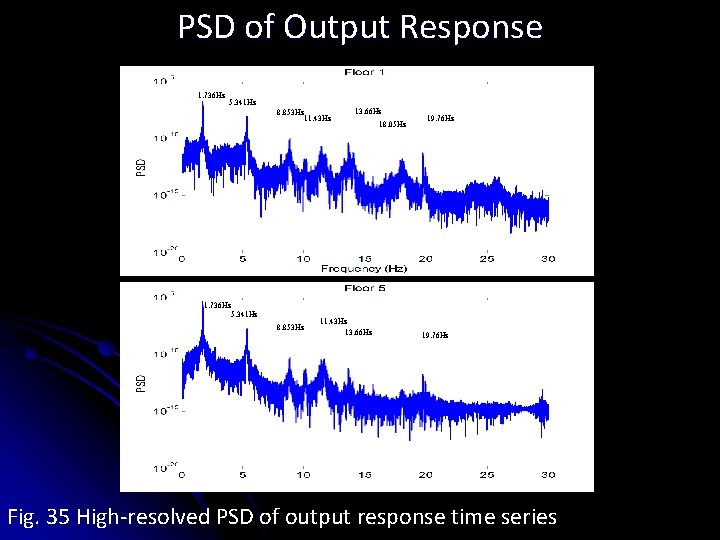
PSD of Output Response 1. 736 Hz 5. 341 Hz 8. 853 Hz 11. 43 Hz 1. 736 Hz 5. 341 Hz 8. 853 Hz 13. 66 Hz 11. 43 Hz 13. 66 Hz 18. 05 Hz 19. 76 Hz Fig. 35 High-resolved PSD of output response time series

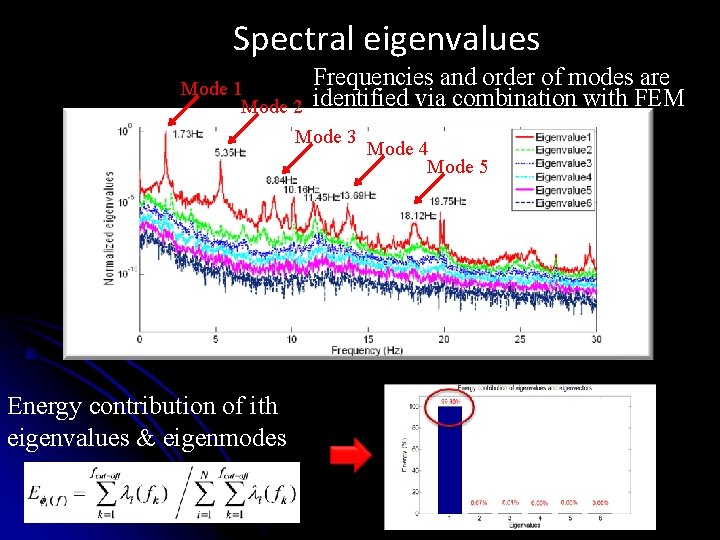
Spectral eigenvalues Frequencies and order of modes are with FEM Mode 1 Mode 2 identified via combination Mode 3 Mode 4 Mode 5 Energy contribution of ith eigenvalues & eigenmodes

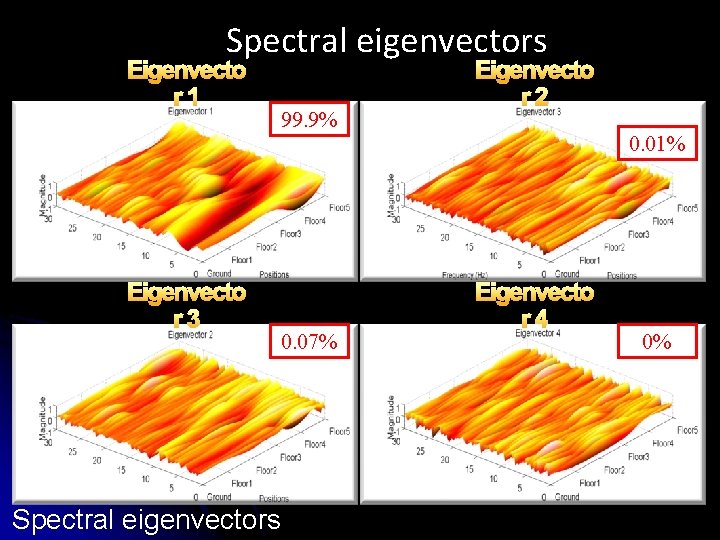
Spectral eigenvectors Eigenvecto r 1 Eigenvecto r 3 99. 9% 0. 07% Spectral eigenvectors Eigenvecto r 2 0. 01% Eigenvecto r 4 0%

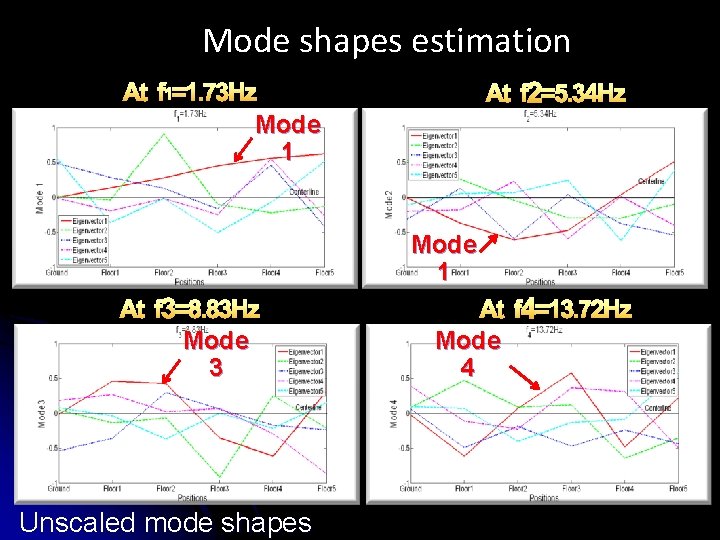
Mode shapes estimation At f 2=5. 34 Hz At f 1=1. 73 Hz Mode 1 At f 3=8. 83 Hz Mode 3 Unscaled mode shapes At f 4=13. 72 Hz Mode 4

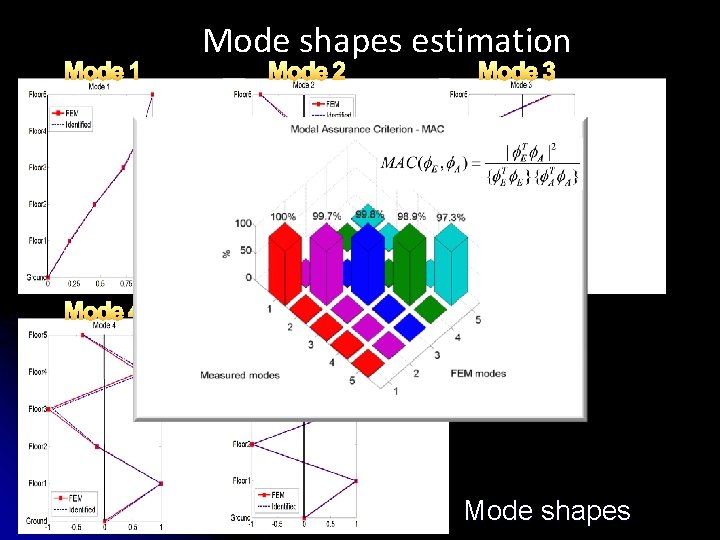
Mode 1 Mode 4 Mode shapes estimation Mode 2 Mode 3 Mode 5 Mode shapes

THANK YOU VERY MUCH FOR YOUR KIND ATTENTION どもありがとう ございます。