Open Channel Flow 1 Uniform flow Mannings Eqn

Open Channel Flow 1. Uniform flow - Manning’s Eqn in a prismatic channel - Q, v, y, A, P, B, S and roughness are all constant 2. Critical flow - Specific Energy Eqn (Froude No. ) 3. Non-uniform flow - gradually varied flow (steady flow) - determination of floodplains 4. Unsteady and Non-uniform flow - flood waves

Uniform Open Channel Flow Manning’s Eqn for velocity or flow where n = Manning’s roughness coefficient R = hydraulic radius = A/P S = channel slope Q = flow rate (cfs) = v A

Uniform Open Channel Flow – Brays Bayou Concrete Channel

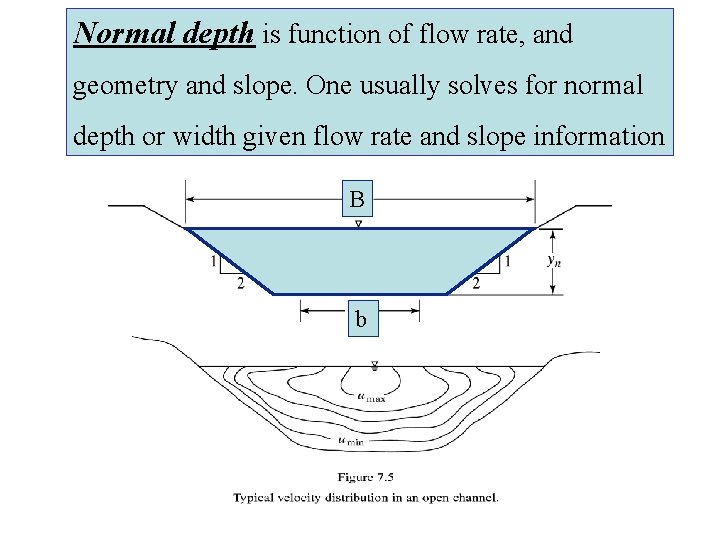
Normal depth is function of flow rate, and geometry and slope. One usually solves for normal depth or width given flow rate and slope information B b

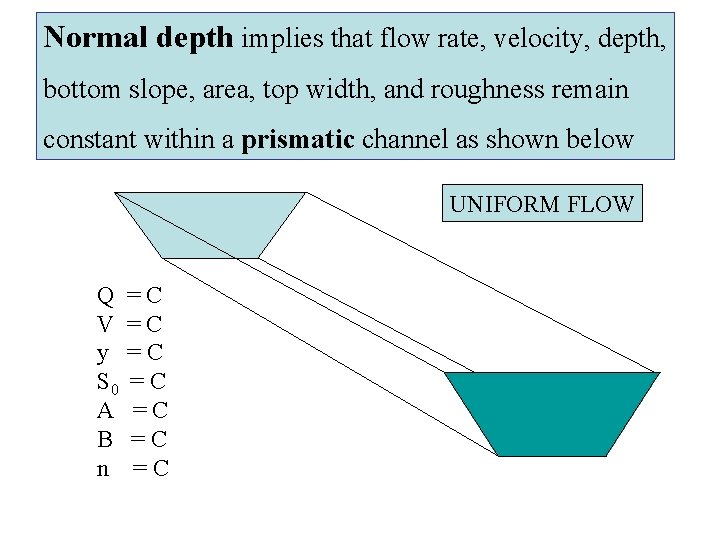
Normal depth implies that flow rate, velocity, depth, bottom slope, area, top width, and roughness remain constant within a prismatic channel as shown below UNIFORM FLOW Q V y S 0 A B n =C =C

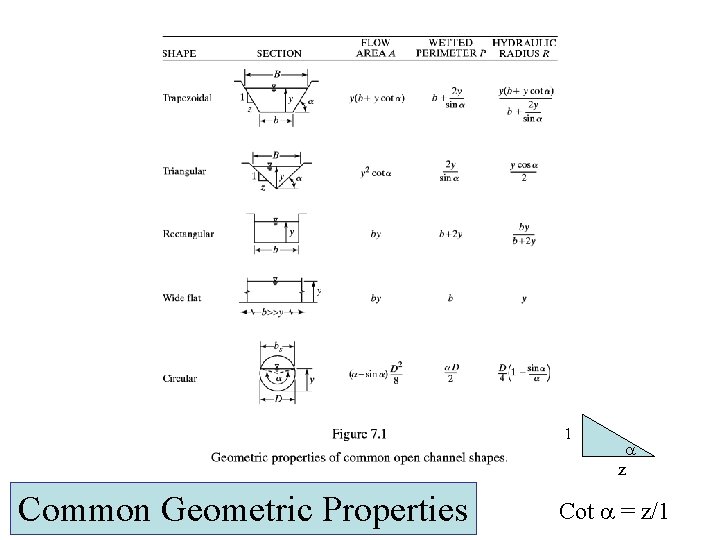
1 z Common Geometric Properties Cot = z/1

Optimal Channels - Max R and Min P

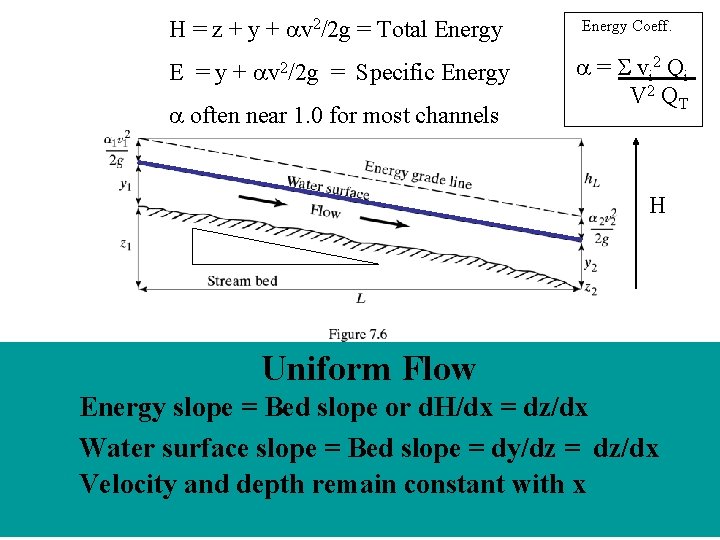
H = z + y + v 2/2 g = Total Energy E = y + v 2/2 g = Specific Energy often near 1. 0 for most channels Energy Coeff. = S vi 2 Qi V 2 QT H Uniform Flow Energy slope = Bed slope or d. H/dx = dz/dx Water surface slope = Bed slope = dy/dz = dz/dx Velocity and depth remain constant with x

My son Eric Critical Depth and Flow

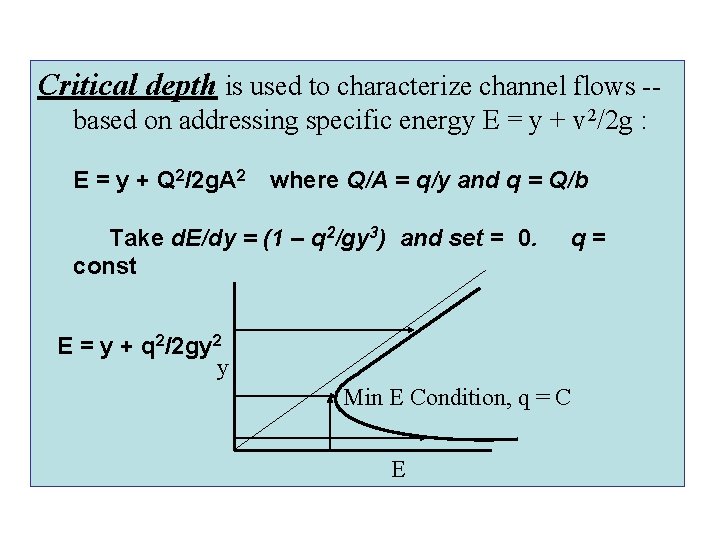
Critical depth is used to characterize channel flows -based on addressing specific energy E = y + v 2/2 g : E = y + Q 2/2 g. A 2 where Q/A = q/y and q = Q/b Take d. E/dy = (1 – q 2/gy 3) and set = 0. const q= E = y + q 2/2 gy 2 y Min E Condition, q = C E

Solving d. E/dy = (1 – q 2/gy 3) and set = 0. For a rectangular channel bottom width b, 1. Emin = 3/2 Yc for critical depth y = yc 2. yc/2 = Vc 2/2 g 3. yc = (Q 2/gb 2)1/3 Froude No. = v/(gy)1/2 We use the Froude No. to characterize critical flows

Y vs E E = y + q 2/2 gy 2 q = const

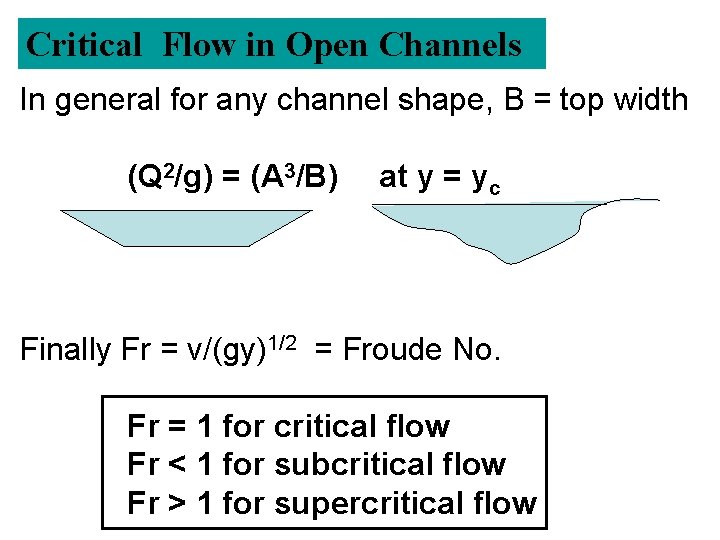
Critical Flow in Open Channels In general for any channel shape, B = top width (Q 2/g) = (A 3/B) at y = yc Finally Fr = v/(gy)1/2 = Froude No. Fr = 1 for critical flow Fr < 1 for subcritical flow Fr > 1 for supercritical flow

Non-Uniform Open Channel Flow With natural or man-made channels, the shape, size, and slope may vary along the stream length, x. In addition, velocity and flow rate may also vary with x. Non-uniform flow can be best approximated using a numerical method called the Standard Step Method.

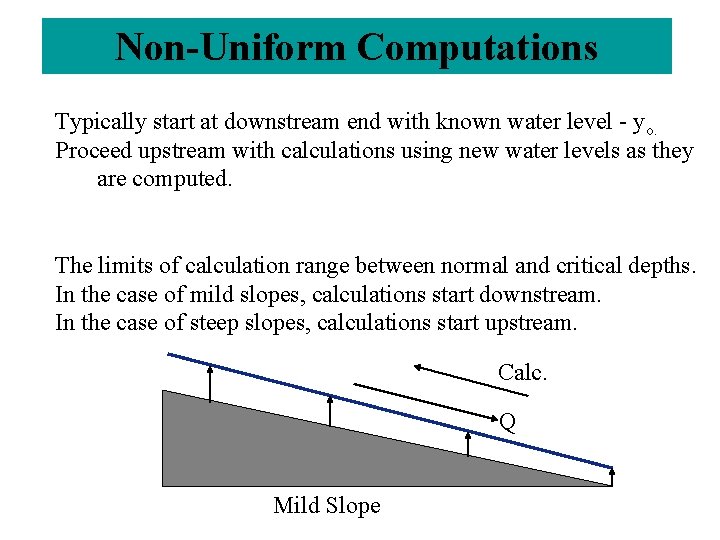
Non-Uniform Computations Typically start at downstream end with known water level - yo. Proceed upstream with calculations using new water levels as they are computed. The limits of calculation range between normal and critical depths. In the case of mild slopes, calculations start downstream. In the case of steep slopes, calculations start upstream. Calc. Q Mild Slope

Non-Uniform Open Channel Flow Let’s evaluate H, total energy, as a function of x. Take derivative, Where H = total energy head z = elevation head, v 2/2 g = velocity head

Replace terms for various values of S and So. Let v = q/y = flow/unit width - solve for dy/dx, the slope of the water surface

Given the Froude number, we can simplify and solve for dy/dx as a fcn of measurable parameters *Note that the eqn blows up when Fr = 1 and goes to �zeroo if = S, the S case of uniform OCF. where S = total energy slope So = bed slope, dy/dx = water surface slope

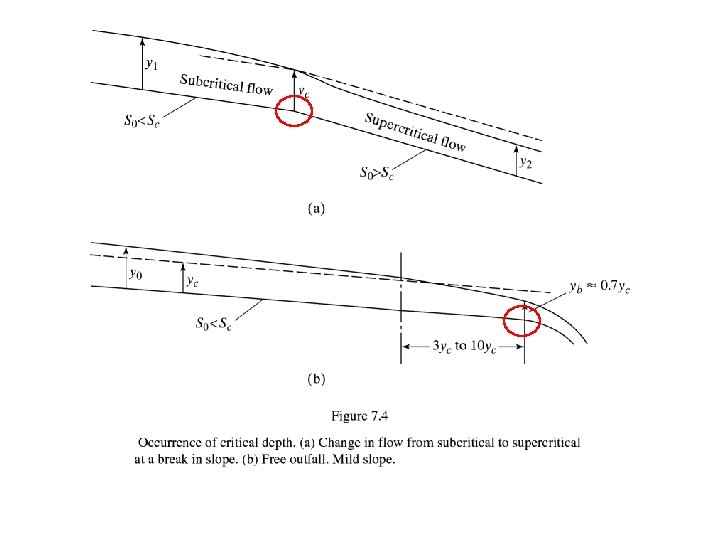
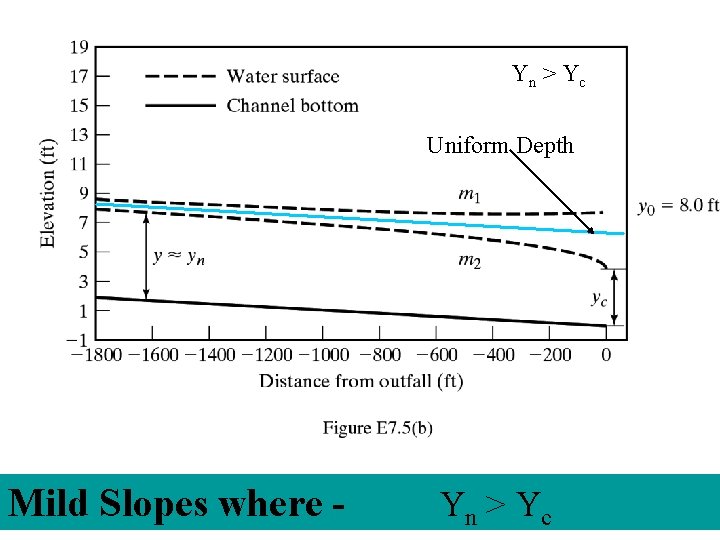
Yn > Y c Uniform Depth Mild Slopes where - Yn > Y c

Now apply Energy Eqn. for a reach of length L This Eqn is the basis for the Standard Step Method Solve for L = x to compute water surface profiles as function of y 1 and y 2, v 1 and v 2, and S 0

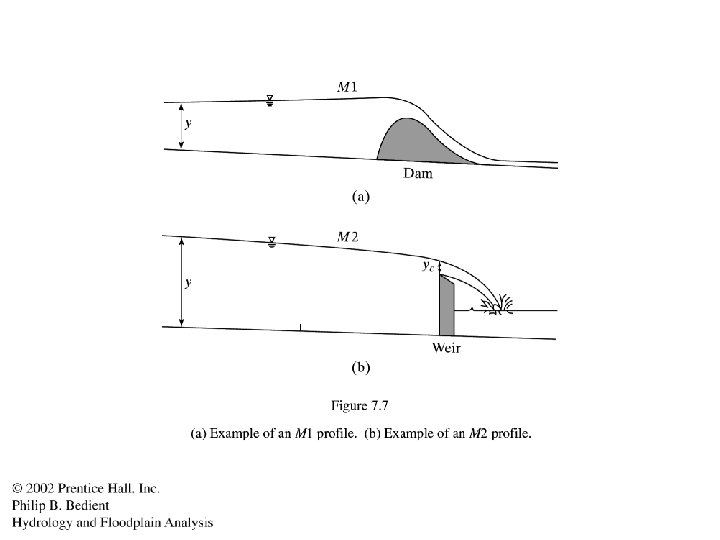
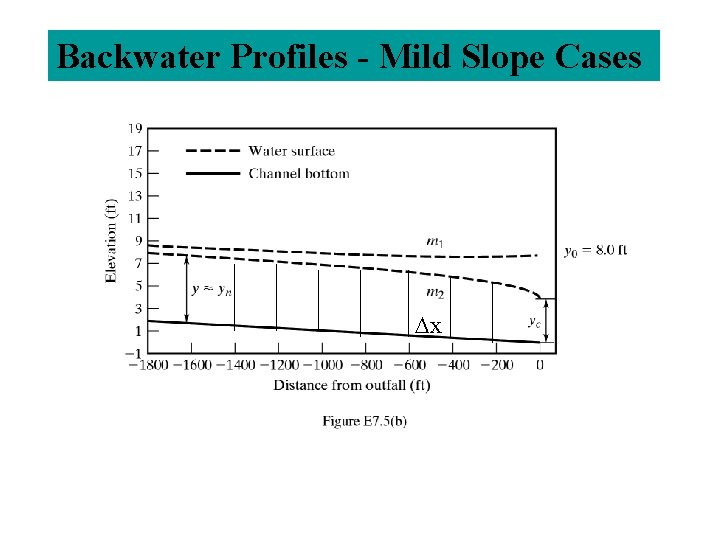
Backwater Profiles - Mild Slope Cases x

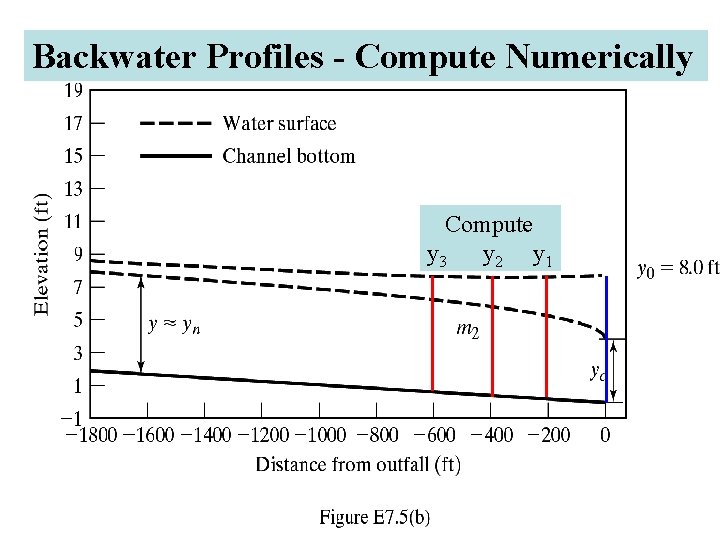
Backwater Profiles - Compute Numerically Compute y 3 y 2 y 1

Routine Backwater Calculations 1. Select Y 1 (starting depth) 2. Calculate A 1 (cross sectional area) 3. Calculate P 1 (wetted perimeter) 4. Calculate R 1 = A 1/P 1 5. Calculate V 1 = Q 1/A 1 6. Select Y 2 (ending depth) 7. Calculate A 2 8. Calculate P 2 9. Calculate R 2 = A 2/P 2 10. Calculate V 2 = Q 2/A 2

Backwater Calculations (cont’d) 1. Prepare a table of values Energy Slope Approx. 2. Calculate Vm = (V 1 + V 2) / 2 3. Calculate Rm = (R 1 + R 2) / 2 4. Calculate Manning’s 5. Calculate L = ∆X from first equation 6. X = ∑∆Xi for each stream reach (SEE SPREADSHEETS)

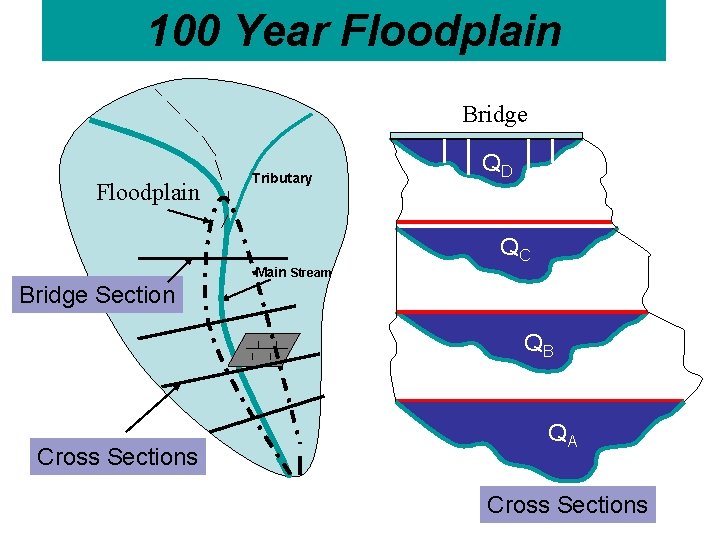
100 Year Floodplain Bridge D Floodplain Tributary C QD QC Main Stream Bridge Section B QB A Cross Sections QA Cross Sections

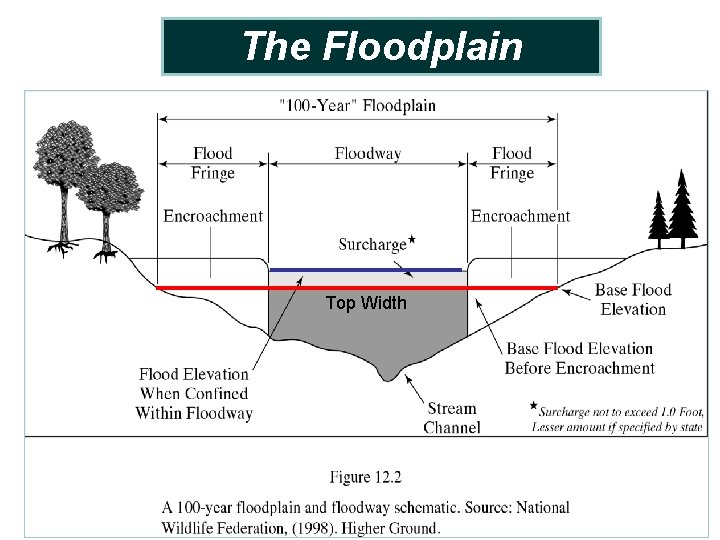
The Floodplain Top Width

Floodplain Determination

The Woodlands v The Woodlands planners wanted to design the community to withstand a 100 -year storm. v In doing this, they would attempt to minimize any changes to the existing, undeveloped floodplain as development proceeded through time.

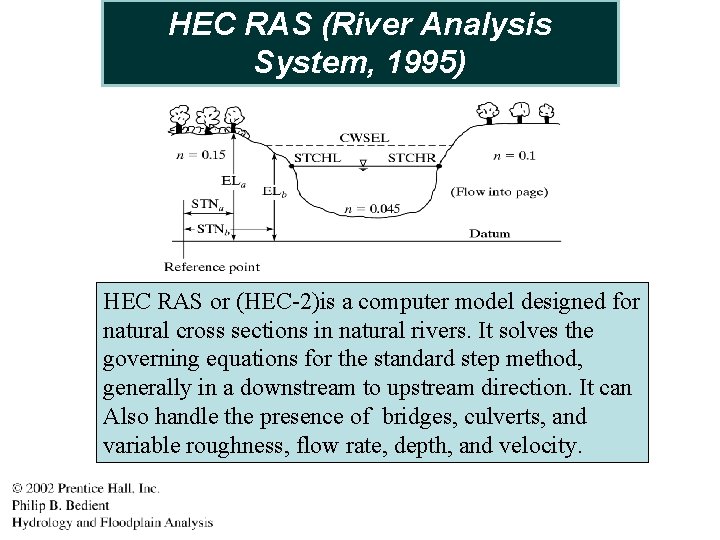
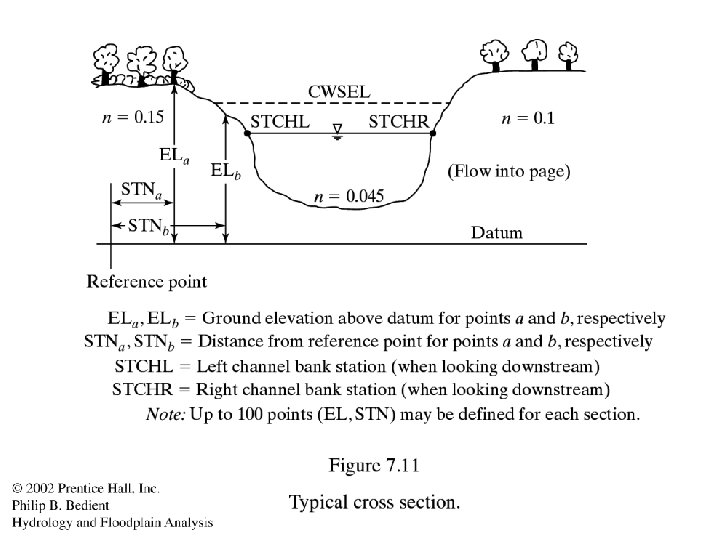
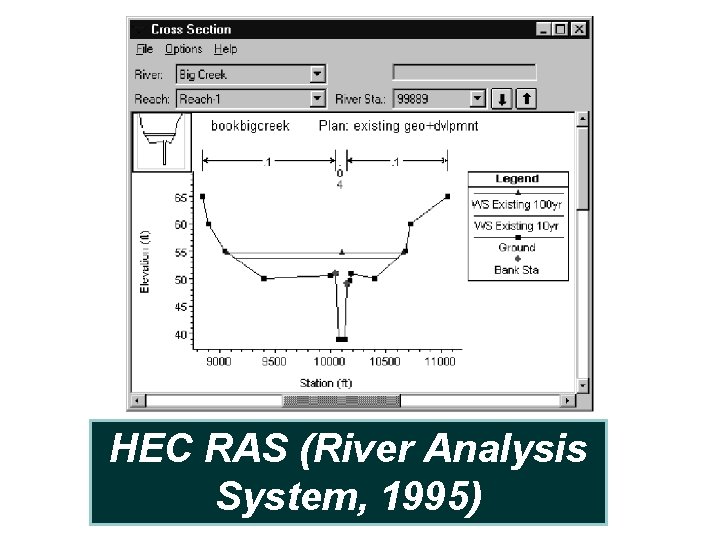
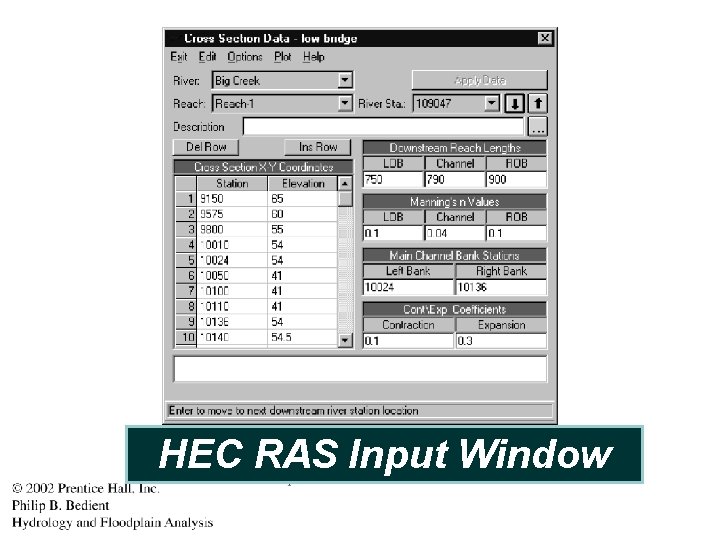
HEC RAS (River Analysis System, 1995) HEC RAS or (HEC-2)is a computer model designed for natural cross sections in natural rivers. It solves the governing equations for the standard step method, generally in a downstream to upstream direction. It can Also handle the presence of bridges, culverts, and variable roughness, flow rate, depth, and velocity.

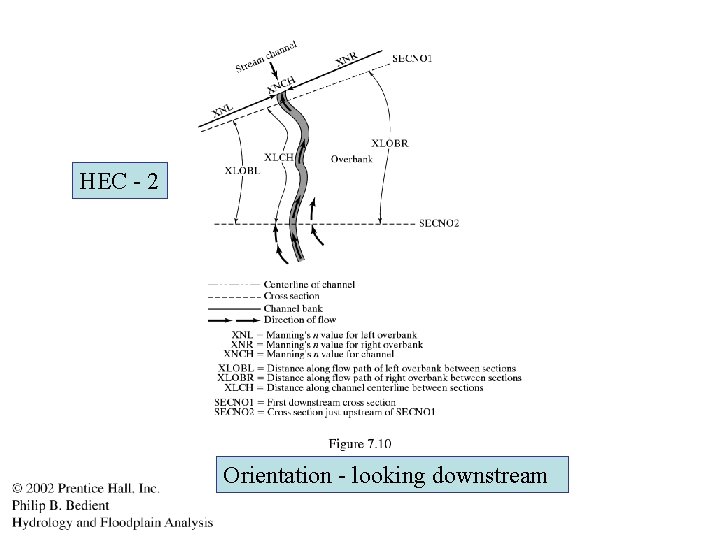
HEC - 2 Orientation - looking downstream

River Multiple Cross Sections

HEC RAS (River Analysis System, 1995)

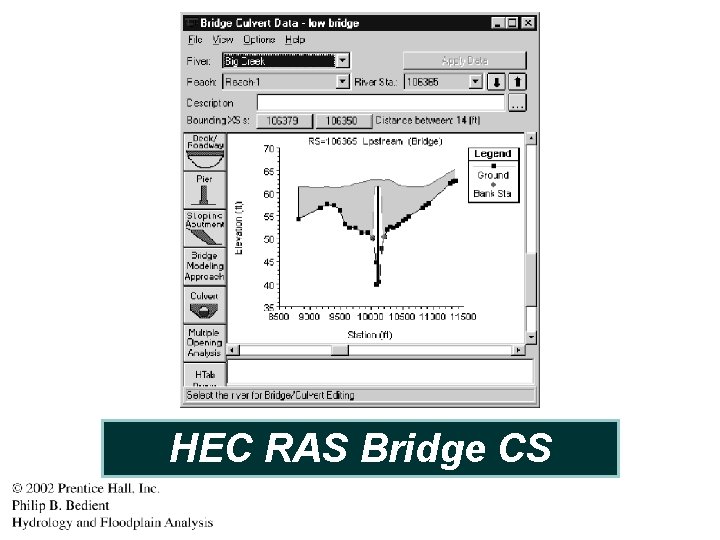
HEC RAS Bridge CS

HEC RAS Input Window

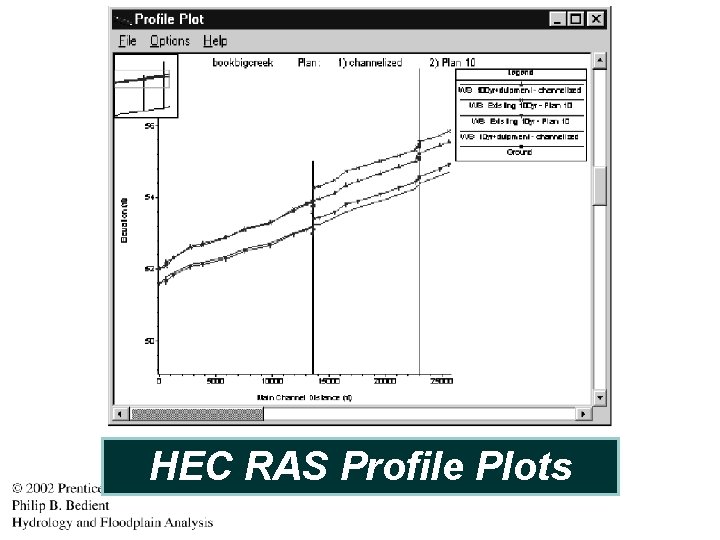
HEC RAS Profile Plots

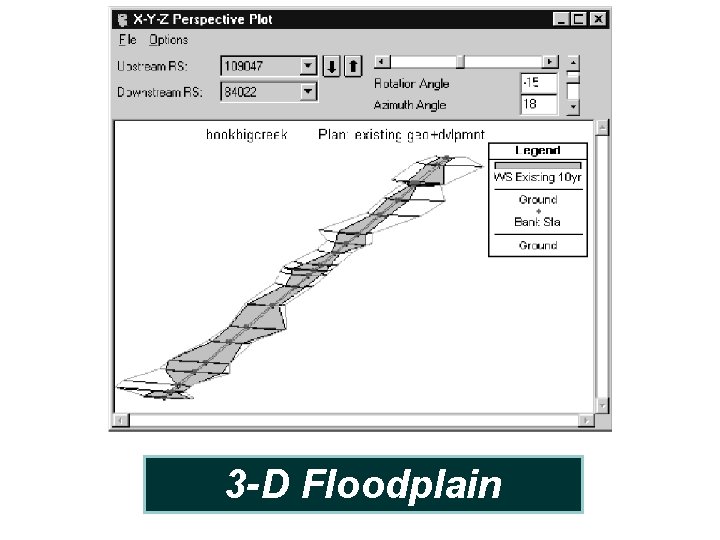
3 -D Floodplain

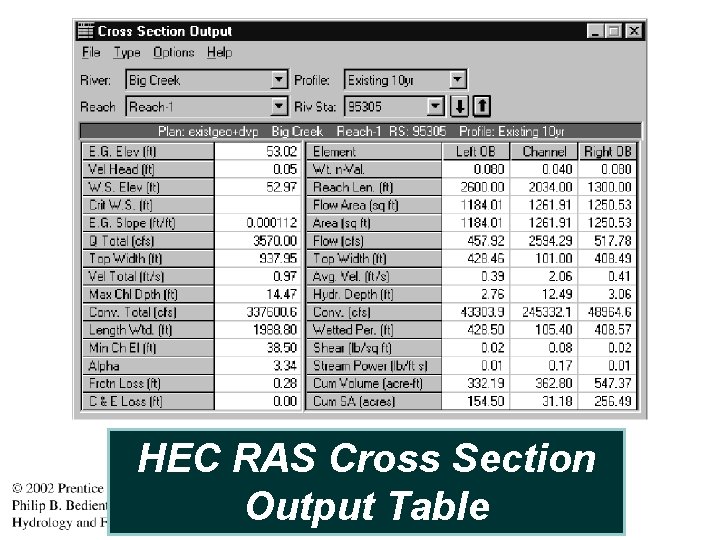
HEC RAS Cross Section Output Table

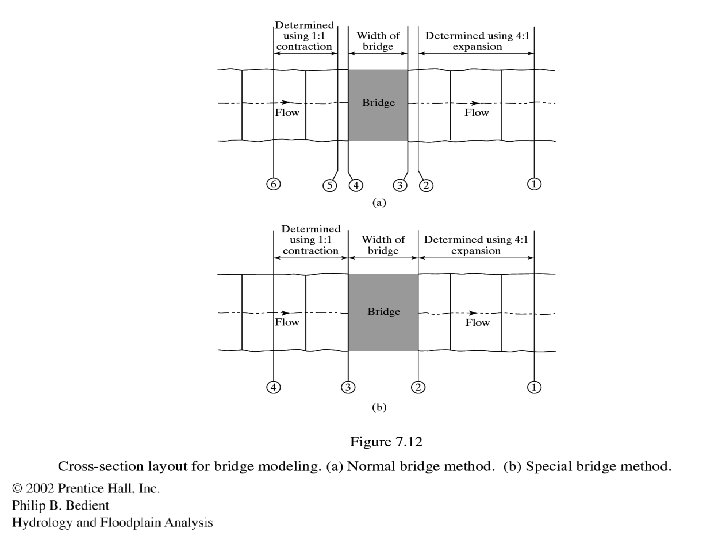
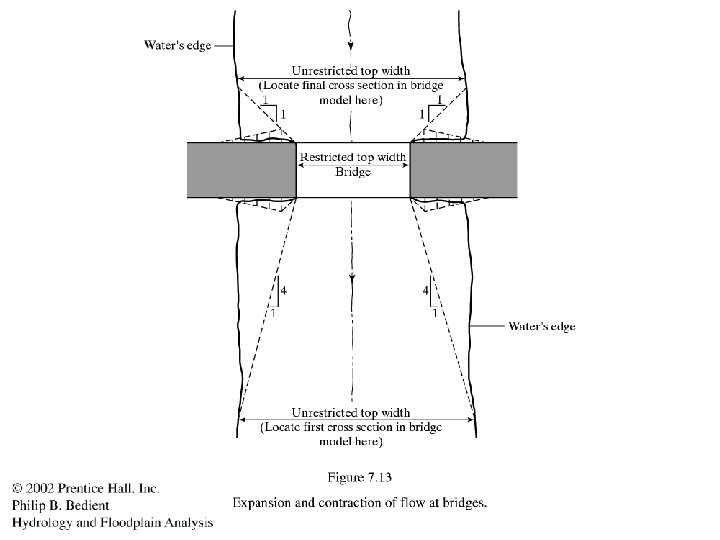
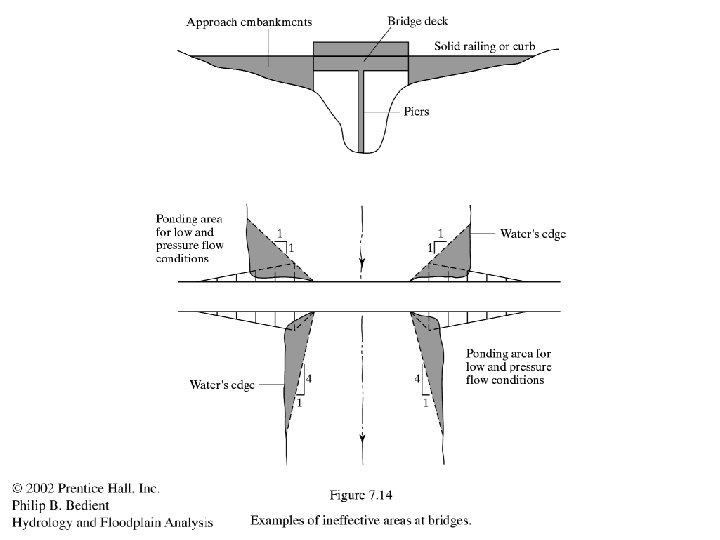
Brays Bayou-Typical Urban System • Bridges cause unique problems in hydraulics Piers, low chords, and top of road is considered Expansion/contraction cause hydraulic losses Several cross sections are needed for a bridge 288 Bridge causes a 2 ft Backup at TMC and is being replaced by TXDOT 288 Crossing