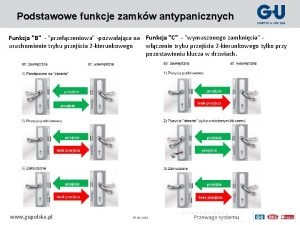
OPCJE OPCJE zagadnienia Funkcja wypaty funkcja zysku Terminy

OPCJE

OPCJE - zagadnienia § § Funkcja wypłaty, funkcja zysku Terminy: in the money, out of the money Rynek doskonały Wzory na wycenę opcji przy założeniu okresowej kapitalizacji odsetek § Wzory na wycenę opcji przy założeniu ciągłej kapitalizacji odsetek § Delta hedging (strategia osłonowa delta) § Algorytm wyceny w ustalonej liczbie etapów

OPCJE / DEFINICJA § Opcja jest prawem do zakupu lub sprzedaży określonej ilości wyspecyfikowanego przedmiotu (tzw. instrumentu bazowego) po z góry ustalonej cenie i w ciągu umówionego okresu lub w wyznaczonym terminie. § Opcja jest to umowa dająca jej posiadaczowi prawo do wykonania określonej czynności w określonym momencie lub przedziale czasu.

CELE ZAWIERANIA KONTRAKTÓW OPCYJNYCH § Zabezpieczenie przed niekorzystnymi zmianami cen instrumentu bazowego § Spekulacje na spadku lub wzroście instrumentu bazowego § Arbitraż między rynkiem instrumentów pochodnych a rynkiem instrumentów bazowych

INSTRUMENTY BAZOWE DLA OPCJI § Waluty opcje na kursy walutowe § Akcje opcje na poszczególne akcje § Obligacje opcje na obligacje § Towary opcje na towary § Stopy procentowe opcje na kontrakty na stopy procentowe

Funkcja wypłaty / europejska opcja kupna K - cena realizacji (wykonania) T - data wygaśnięcia opcji ST - cena w momencie T waloru bazowego, na który wystawiona jest opcja Jeśli w chwili T cena rynkowa waloru (ST) jest większa od ceny wykonania K , to posiadający opcję kupna uzyskuje kwotę ST - K , ( opcja daje mu prawo do zakupienia waloru za cenę K, który może sprzedać po cenie rynkowej wynoszącej ST ). Jeśli ST ≤ K, to opcja kupna jest bezwartościowa i nie zostanie zrealizowana. Niech C oznaczać będzie cenę opcji kupna a P będzie ceną opcji sprzedaży

Funkcja wypłaty / europejska opcja kupna Definicja Funkcję zdefiniowaną wzorem lub nazywamy funkcją wypłaty dla posiadacza opcji kupna.

Funkcja wypłaty / europejska opcja sprzedaży Funkcję zdefiniowaną wzorem lub nazywamy funkcją wypłaty dla posiadacza opcji sprzedaży.

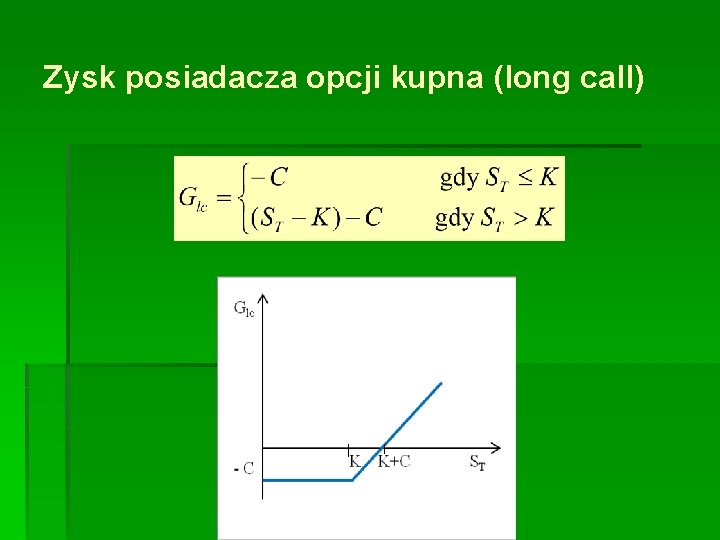
Zysk posiadacza opcji kupna (long call)

Zysk wystawcy opcji kupna (short call) C – cena opcji kupna (premia)

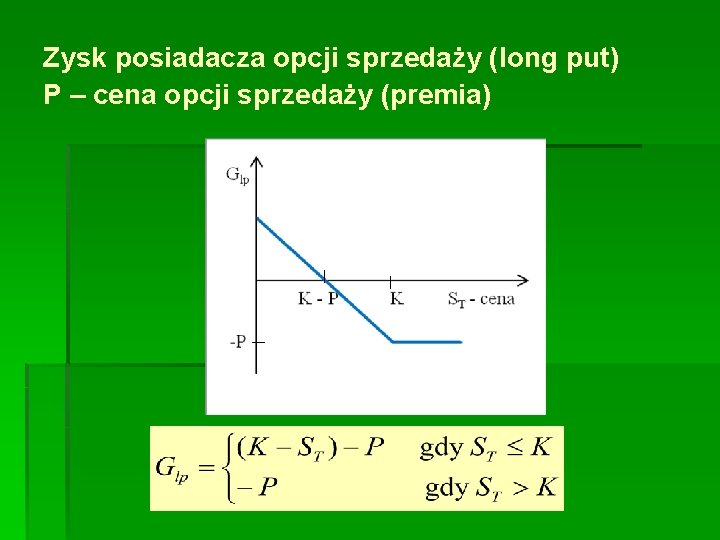
Zysk posiadacza opcji sprzedaży (long put) P – cena opcji sprzedaży (premia)

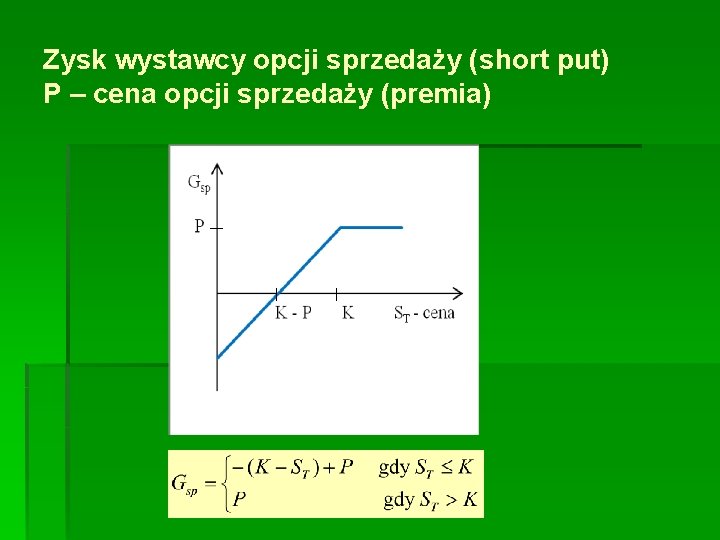
Zysk wystawcy opcji sprzedaży (short put) P – cena opcji sprzedaży (premia)

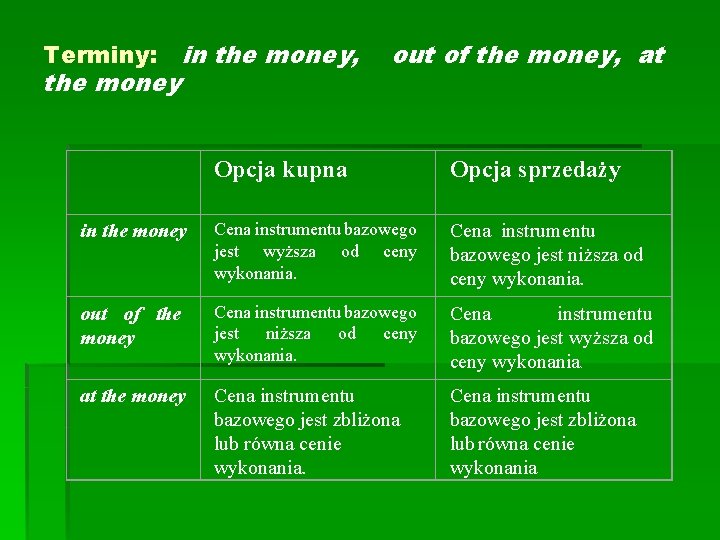
Terminy: the money in the money, out of the money, at Opcja kupna Opcja sprzedaży in the money Cena instrumentu bazowego jest wyższa od ceny wykonania. Cena instrumentu bazowego jest niższa od ceny wykonania. out of the money Cena instrumentu bazowego jest niższa od ceny wykonania. Cena instrumentu bazowego jest wyższa od ceny wykonania. at the money Cena instrumentu bazowego jest zbliżona lub równa cenie wykonania

Wycena opcji – model dwumianowy założenia o rynku doskonałym oprocentowanie depozytów i kredytów bankowych jest jednakowe wysokość zaciąganych kredytów nie jest ograniczona zapewniona jest płynność obrotu wszystkimi aktywami nie ma żadnych kosztów związanych z zawieraniem transakcji wszystkie aktywa są doskonale podzielne dopuszczalna jest krótka sprzedaż aktywów brak jest możliwości arbitrażu

Model dwustanowy jednookresowy wyceny opcji kupna. Kapitalizacja okresowa Cel: określenie ceny opcji kupna C 0 Dane: cena realizacji - K cena początkowa akcji - S 0 cena akcji po upływie okresu w przypadku wzrostu w przypadku spadku stopa wolna od ryzyka - r Zakładamy ponadto że - wycena będzie dokonana w warunkach obojętności wobec ryzyka, tzn. cena opcji nie będzie zależała od późniejszego zachowania akcji - akcja nie przynosi dywidendy - rynek jest doskonały - kapitalizacja okresowa

Model dwustanowy jednookresowy wyceny opcji kupna. Przykład cena realizacji – 110 zł cena początkowa akcji - 100 zł cena akcji po upływie okresu w przypadku wzrostu – 150 zł w przypadku spadku – 70 zł okresowa stopa wolna od ryzyka - 20 %

Model dwustanowy jednookresowy wyceny opcji kupna. Przykład Wartość opcji (funkcja wypłaty) po upływie jednego okresu w przypadku wzrostu ceny akcji Wartość opcji (funkcja wypłaty) po upływie jednego okresu w przypadku spadku ceny akcji

Model dwustanowy jednookresowy wyceny opcji kupna. Przykład § Rozważmy portfel składający się z jednej opcji kupna w pozycji krótkiej oraz pewnej liczby akcji, którą oznaczamy symbolem ∆0 § Wartość portfela po upływie jednego okresu będzie wynosić: - gdy cena akcji wzrośnie - gdy cena akcji spadnie.

Model dwustanowy jednookresowy wyceny opcji kupna. Przykład Zgodnie z założeniami portfel ma być wolny od ryzyka, czyli spełniać warunek oznacza to, że Stąd ∆0 = 0, 5 Portfel powinien składać się z długiej pozycji w akcjach w liczbie 0, 5 oraz z krótkiej pozycji opcji kupna w liczbie 1. W obu przypadkach (wzrostu bądź spadku ceny akcji) wartość portfela po upływie jednego okresu wynosi 35 zł.

Model dwustanowy jednookresowy wyceny opcji kupna. Przykład Aby po jednym okresie uzyskać z lokaty 35 zł należy w chwili początkowej zainwestować kwotę: Oznacza to, że wartość jego portfela (∆0 , - 1) w chwili początkowej musi być równa V 0 = 29, 17 zł. (Portfel jest wolny od ryzyka, dlatego jego okresowa stopa zwrotu musi być równa 20%). Z drugiej strony wartość portfela w chwili początkowej można przedstawić w postaci stąd C 0 = 20, 83

Model dwustanowy jednookresowy wyceny opcji kupna. Przykład § Cena opcji C 0 = 20, 83 zł jest tzw. ceną arbitrażową, lub ceną fair. § Gdyby cena opcji była większa, to inwestor potrzebowałby mniej niż 29, 17 zł na konstrukcję portfela w chwili początkowej, zatem roczny zysk byłby większy niż 20%, czyli. istniałaby możliwość arbitrażu. (C 0 = 22, to wartość portfela początkowego 28 zł, końcowego 35, zysk 25%) § Gdyby cena opcji była mniejsza niż 20, 83 zł , (np. 20 zł) to inwestor powinien zająć pozycję odwrotną (krótka sprzedaż 0, 5 akcji, kupno opcji, zdeponowanie pozostałych pieniędzy (30 zł) na koncie). Po okresie należy odkupić 0, 5 akcji za 75 zł i uzyskać z opcji 40 zł (w przypadku zwyżki), bądź odkupić 0, 5 akcji za 35 zł w przypadku zniżki, zatem wydać w obu sytuacjach 35 zł. Ale po upływie okresu depozyt jest wart 36 zł. Otrzymujemy arbitrażowy zysk w wysokości 1 zł.

Model dwustanowy jednookresowy wyceny opcji kupna. Przypadek ogólny Rozważmy - jak w przykładzie - portfel składający się z jednej opcji kupna w pozycji krótkiej oraz pewnej liczby akcji ∆0 Portfel ma być wolny od ryzyka tzn: czyli gdzie

Model dwustanowy jednookresowy wyceny opcji kupna. Przypadek ogólny Gdyby d > 1+r, to możliwy byłby arbitraż polegający na możliwości zaciągnięcia nieograniczonego kredytu przy stopie r oraz inwestycja w akcje. Gdyby 1+r >u, to możliwy byłby arbitraż polegający na krótkiej sprzedaży akcji i ulokowanie pieniędzy na lokacie o oprocentowaniu r.

Model dwustanowy jednookresowy wyceny opcji kupna. Przypadek ogólny Skoro portfel jest wolny od ryzyka, jego roczna stopa zwrotu musi być równa stopie zwrotu wolnej od ryzyka. Zatem: wart. końc. portf. /(1+r)= wart. początk. portf. Stąd wyliczając C 0 otrzymujemy (uwzględniając wzór na delta)

Po uproszczeniach otrzymujemy

Model dwustanowy jednookresowy wyceny opcji kupna. Przypadek ogólny. Podsumowanie Cena europejskiej opcji kupna w dwustanowym modelu jednookresowym (przy wcześniejszych oznaczeniach) dana jest wzorem zatem

Model dwustanowy jednookresowy wyceny opcji sprzedaży. Cena europejskiej opcji sprzedaży z ceną realizacji K w jednookresowym modelu dwumianowym wynosi: gdzie P 1 u oraz P 1 u oznaczają wartości opcji sprzedaży odpowiednio po wzroście lub spadku akcji, czyli Dowód w przypadku opcji sprzedaży można uzyskać naśladując postępowanie z dowodu dla opcji kupna

Model dwustanowy jednookresowy wyceny opcji kupna. UWAGI 1. Wzór określający cenę opcji kupna nie zawiera wartości prawdopodobieństw wzrostu ani spadku ceny akcji. 2. Liczby p i (1 -p) można interpretować jako prawdopodobieństwo (odpowiednio) wzrostu, spadku ceny akcji Przy interpretacji liczb p i (1 -p) jako prawdopodobieństwa, cena opcji kupna jest oczekiwaną wartością funkcji wypłaty zdyskontowaną czynnikiem 1/(1+ r).

Model dwustanowy jednookresowy wyceny opcji kupna. UWAGI Przy interpretacji probabilistycznej liczb p i (1 - p) wartość oczekiwana ceny akcji po jednym okresie jest równa wartości przyszłej kwoty S 0. Dowód

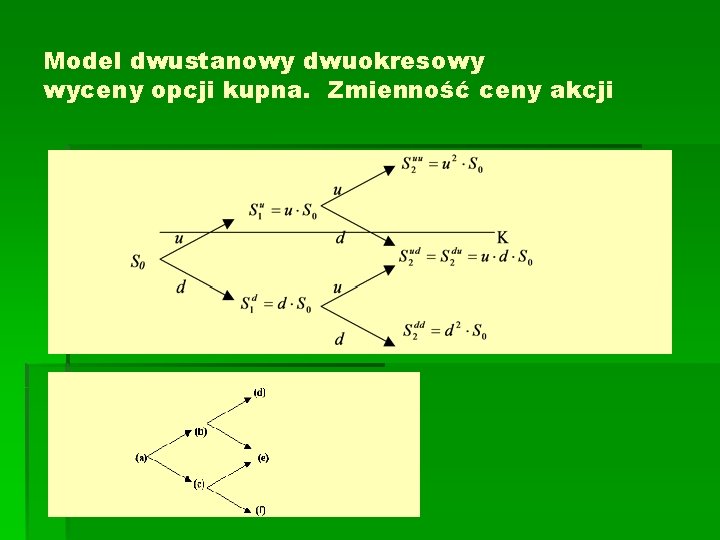
Model dwustanowy dwuokresowy wyceny opcji kupna. Zmienność ceny akcji

Model dwustanowy dwuokresowy § gdzie

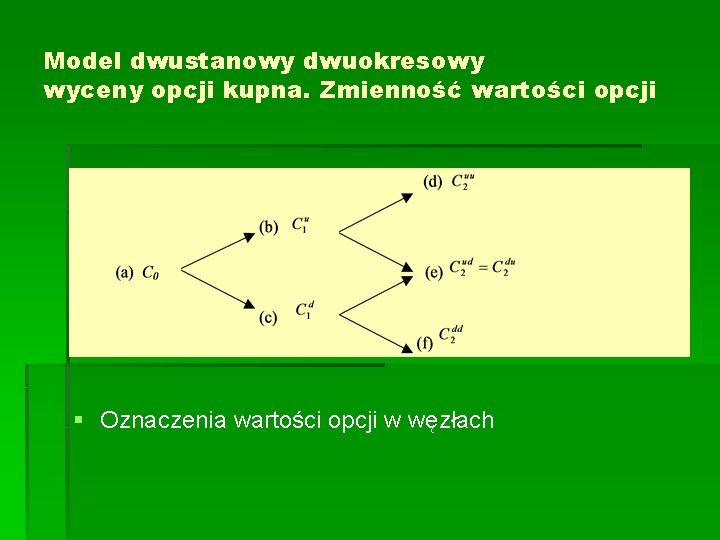
Model dwustanowy dwuokresowy wyceny opcji kupna. Zmienność wartości opcji § Oznaczenia wartości opcji w węzłach

Model dwustanowy dwuokresowy Stosując wzór na wycenę opcji kupna w modelu jednookresowym dla węzłów (b), (c) otrzymujemy Znając te wyceny można wyznaczyć cenę opcji w chwili początkowej - czyli w węźle (a)

Model dwustanowy dwuokresowy Podstawiając dwa poprzednie wzory do ostatniego otrzymujemy Mamy więc

Model dwustanowy dwuokresowy 1. Podobnie jak dla wyceny opcji w modelu jednookresowym liczby można interpretować jak prawdopodobieństwa odpowiednio dwukrotnego wzrostu , wzrostu i spadku oraz dwukrotnego spadku akcji. 2. Wzór na wycenę opcji można przedstawić następująco lub z użyciem dwumianu Newtona

Model dwustanowy n – okresowy Uogólnienie wzoru na wycenę opcji kupna dla modelu dwuokresowego Wzór na wycenę opcji kupna w modelu dwuokresowym można uogólnić (metodą indukcyjną) na przypadek modelu n - okresowego:

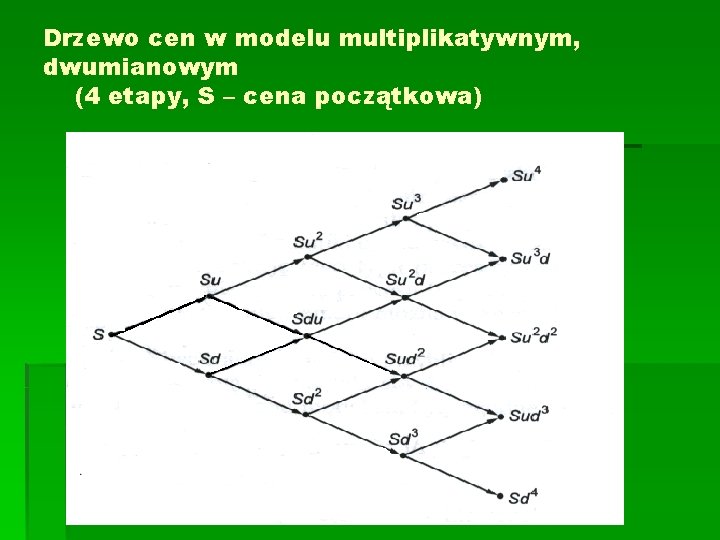
Drzewo cen w modelu multiplikatywnym, dwumianowym (4 etapy, S – cena początkowa)

Ceny końcowe akcji w modelu multiplikatywnym dwumianowym, n-etapowym Możliwe ceny końcowe muszą mieć postać Sukdn-k, gdzie k = 0, 1, …, n. Na drzewie cenowym istnieje różnych dróg prowadzących do węzła identyfikowanego z ceną Sukdn-k , gdyż każda droga jest jednoznacznie scharakteryzowana przez nwyrazowy ciąg (u, u, d, u, …, d, u), zawierający k liter u oraz (n-k) liter d.

Ceny końcowe w modelu multiplikatywnym dwumianowym, n-etapowym § Prawdopodobieństwo każdej takiej drogi – jako koniunkcji zdarzeń niezależnych - wynosi § pk (1 -p)n-k Zatem prawdopodobieństwo ceny końcowej S 0 ukdn-k wynosi §

Interpretacja wzoru na wycenę opcji kupna w modelu n - okresowym Jeżeli p potraktujemy jak prawdopodobieństwo wzrostu akcji, to liczba dana wyżej jest prawdopodobieństwem uzyskania ceny końcowej akcji ukdn-k. S 0, zaś liczba max(ukdn-k. S 0 -K, 0) jest wartością (funkcją wypłaty) opcji kupna przy tej cenie akcji. Cena opcji kupna C 0 jest więc równa wartości bieżącej oczekiwanej funkcji wypłaty.

Model dwustanowy n – okresowy Wzór na wycenę opcji sprzedaży Jeżeli p potraktujemy jako prawdopodobieństwo wzrostu akcji, to liczba P 0 jest równa zaktualizowanej na moment początkowy oczekiwanej wartości funkcji wypłaty opcji sprzedaży. Liczba Max(K-ukdn-k. S 0, 0) jest wartością (funkcją wypłaty) opcji sprzedaży przy cenie akcji ukdn-k. S 0.

Wzory na wycenę opcji przy założeniu ciągłej kapitalizacji odsetek § W modelu jednookresowym § W modelu wielookresowym

Porównanie wzorów w modelu jednookresowym kapitalizacja ciągła, kapitalizacja roczna

Model dwumianowy wyceny opcji ciągła kapitalizacja odsetek TW. Wartość opcji w modelu jednookresowym dwumianowym jest dana wzorem C = e – r. T [p Cu +(1 -p) Cd ] gdzie p = (e r. T – d)/(u – d) Dowód. § Rozważmy portfel składający się z ∆ akcji (długa pozycja) i jednej opcji (krótka pozycja). § Obliczymy wartość ∆, dla której portfel ten jest wolny od ryzyka. § W przypadku wzrostu ceny akcji wartość portfela w momencie wygaśnięcia opcji jest równa Su∆ - Cu zaś w drugim przypadku Sd∆ - Cd.

Model dwumianowy wyceny opcji ciągła kapitalizacja odsetek Obojętność wobec ryzyka wymaga by wartości te były równe; Su ∆ - Cu = Sd ∆ - Cd. Zatem liczba akcji w portfelu wynosi ∆ = (Cu-Cd) / (Su – Sd) Bieżąca wartość rozpatrywanego portfela (Su∆ - Cu)e – r. T. Ponieważ początkowy koszt utworzenia portfela wynosił S∆ - C, mamy więc równość S∆ - C = (Su∆ - Cu ) e – r. T S∆ - (Su∆ - Cu ) e – r. T = C S∆ e r. T - (Su∆ - Cu ) = C e r. T ∆(S e r. T – Su) + Cu = C e r. T

Model dwumianowy wyceny opcji ciągła kapitalizacja odsetek ∆(S e r. T – Su) + Cu = C e r. T podstawiając ∆ = (Cu-Cd) / S(u – d) równanie przyjmie postać: C e r. T = (Cu-Cd) S (e r. T – u) /S(u – d) + Cu C e r. T = (Cu-Cd) (e r. T – u) /(u – d) + (u – d)Cu/(u – d) C e r. T = [Cu e r. T - Cd e r. T – Cu u + Cd u + u Cu – d. Cu ]/(u – d) C e r. T = [Cu e r. T - Cd e r. T + Cd u – d. Cu ]/(u – d) C e r. T = Cu (e r. T –d) )/(u – d) + Cd (u-e r. T )/(u – d) C = e – r. T [p Cu +(1 -p) Cd ] gdzie p = (e r. T –d)/(u – d), 1 - p = (u-d- er. T +d)/(u – d)= (u- er. T )/(u – d)

Porównanie wzorów w modelu n – okresowym kapitalizacja ciągła, kapitalizacja roczna

UWAGI O DELCIE (delta hedging) W analizie jednookresowego modelu wyceny opcji ustaliliśmy liczbę akcji przypadającej na jedną opcję w pozycji krótkiej Jest on jednocześnie proporcją liczby akcji do liczby opcji (w pozycji krótkiej) dla portfela całkowicie zabezpieczonego (hedge ratio). W modelu wielookresowym delta może być różna w każdym węźle siatki zmienności ceny akcji (zatem dla każdego etapu, dla każdej sytuacji) Jeżeli w każdym momencie portfel akcji i opcji ma być całkowicie zabezpieczony, należy modyfikować jego skład w zależności od scenariusza zmiany ceny akcji.

Drzewo cen w modelu multiplikatywnym, dwumianowym (4 etapy, S – cena początkowa)

UWAGI O DELCIE (delta hedging) § Po k – tym okresie istnieje k+1 węzłów w przyjętym modelu zmienności akcji, które odpowiadają różnym, zrealizowanym do tego momentu scenariuszom. W każdym węźle wielkość delty może być inna. Można przyjąć, że w poniższym wzorze i=1 odpowiada scenariuszowi samych (dotychczasowych) spadków, zaś i = k+1 – samych wzrostów

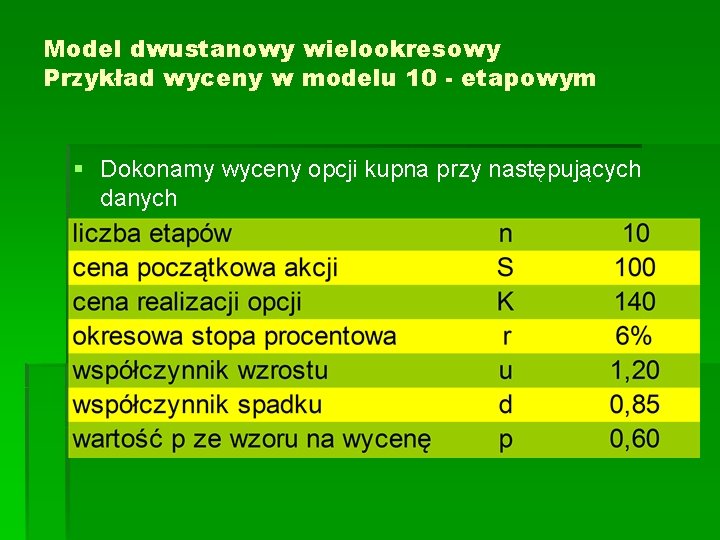
Model dwustanowy wielookresowy Przykład wyceny w modelu 10 - etapowym § Dokonamy wyceny opcji kupna przy następujących danych

Model dwustanowy wielookresowy Algorytm wyceny w modelu 10 – etapowym § Zbudowanie siatki cen akcji w modelu dwumianowym § Ustalenie funkcji wypłaty opcji ( max{ cena końcowa akcji – cena realizacji opcji, zero}) § Wycena opcji w węzłach sieci etapu 9, ze wzoru na wycenę w modelu jednoetapowym § Wycena opcji w węzłach sieci etapu 8, ze wzoru na wycenę w modelu jednoetapowym § Itd. § Wycena opcji w momencie początkowym

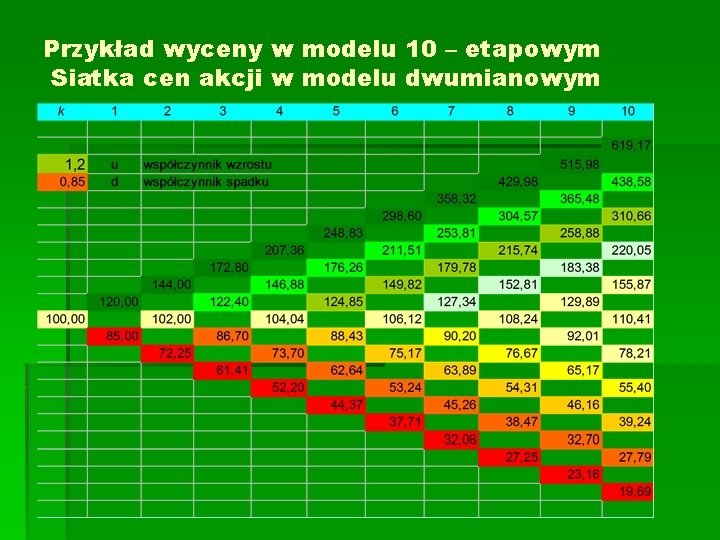
Przykład wyceny w modelu 10 – etapowym Siatka cen akcji w modelu dwumianowym

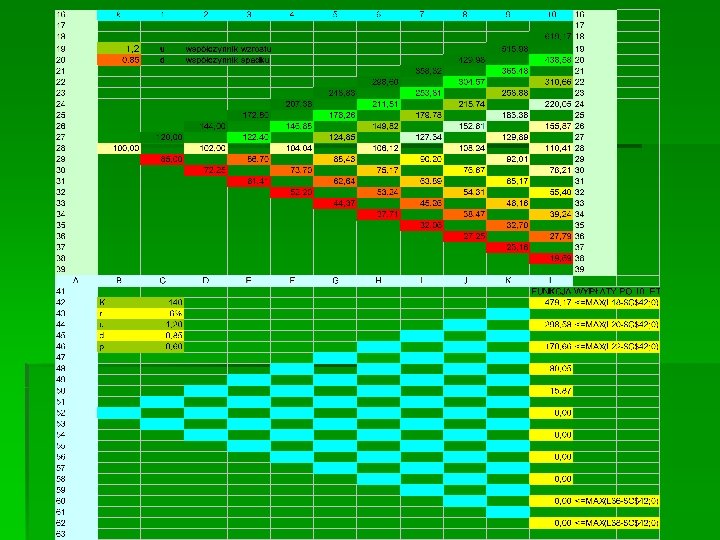
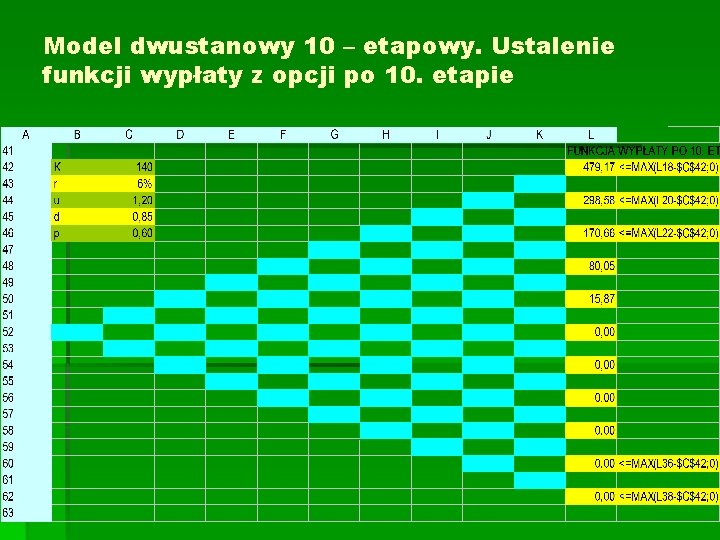
Model dwustanowy 10 – etapowy. Ustalenie funkcji wypłaty z opcji po 10. etapie

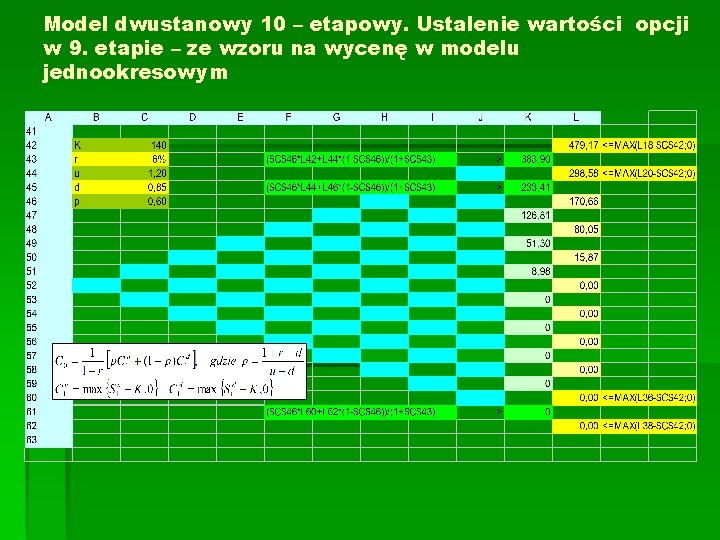
Model dwustanowy 10 – etapowy. Ustalenie wartości opcji w 9. etapie – ze wzoru na wycenę w modelu jednookresowym

Model dwustanowy 10 – etapowy. Ustalenie wartości opcji w każdym etapie, w kazdej sytuacji ( ze wzoru na wycenę w modelu jednookresowym)

Model dwustanowy 10 – etapowy. Ustalenie wartości opcji na podstawie wzoru

Wartość wewnętrzna i wartość czasowa Wartość wewnętrzna opcji jest to różnica między ceną instrumentu bazowego, a ceną wykonania w przypadku opcji kupna, natomiast w przypadku opcji sprzedaży wartość wewnętrzna jest równa różnicy między ceną wykonania, a ceną instrumentu bazowego. Wartość czasowa (zewnętrzna) opcji jest to różnica między ceną opcji (premią), a jej wartością wewnętrzną jeśli różnica ta jest nieujemna w przeciwnym razie wartość czasowa jest równa zeru.

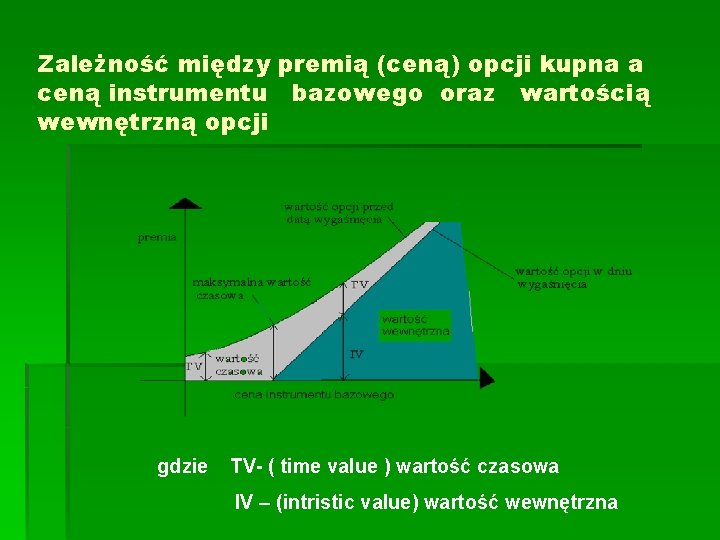
Zależność między premią (ceną) opcji kupna a ceną instrumentu bazowego oraz wartością wewnętrzną opcji gdzie TV- ( time value ) wartość czasowa IV – (intristic value) wartość wewnętrzna

Wycena opcji § J. C. Cox, S. A. Ross, M. Rubinstein Wycena opcji europejskiej w modelu dyskretnym § Fischer Black, Myron Sholes, Robert Merton (1973) Wycena opcji europejskiej w modelu ciągłym § Fischer Black, Myron Sholes Nagroda Nobla 1997 - za nową metodę wyceny instrumentów pochodnych