OnShell Meets Observation or the Rubber Meets the

On-Shell Meets Observation or, the Rubber Meets the Road David A. Kosower Institut de Physique Théorique, CEA–Saclay on behalf of the Black. Hat Collaboration Carola Berger, Z. Bern, L. Dixon, Fernando Febres Cordero, Darren Forde, Harald Ita, DAK, Daniel Maître, Tanju Gleisberg at the Hidden Structures in Field Theory Amplitudes Workshop Niels Bohr Institute, Copenhagen, Denmark August 12, 2009

November 16? Campbell, Huston & Stirling ‘ 06 On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Backgrounds at the LHC • Basic tools: Parton shower programs (Pythia, Herwig, Sherpa) – Leading-order parton-level codes (MADGRAPH; Comp. HEP; AMEGIC++; ALPGEN; HELAC; O’MEGA) – Parton shower programs with matching to leading-order matrix elements – • These give a basic description of a given background • A process with n jets starts at O(α sn), and has an expansion, σ LO α sn(μ) + σ NLO(μ) α sn+1(μ) + σ NNLO(μ) α sn+2(μ) + … but at leading order the description is not quantitative because of the renormalization-scale dependence On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

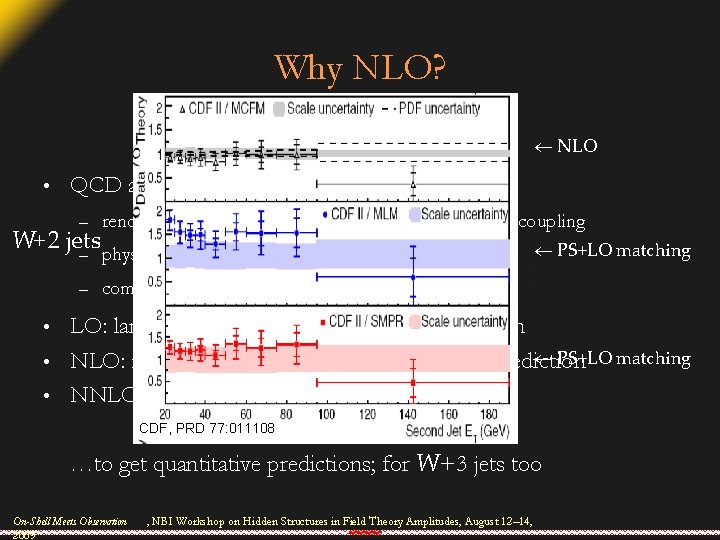
Why NLO? NLO • QCD at LO is not quantitative – renormalization scale enters into the definition of the coupling – physical quantities are independent of it – computations to fixed order are not W+2 jets PS+LO matching LO: large dependence, no quantitative prediction PS+LO matching • NLO: reduced dependence, first quantitative prediction • NNLO: precision prediction • CDF, PRD 77: 011108 …to get quantitative predictions; for W+3 jets too On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

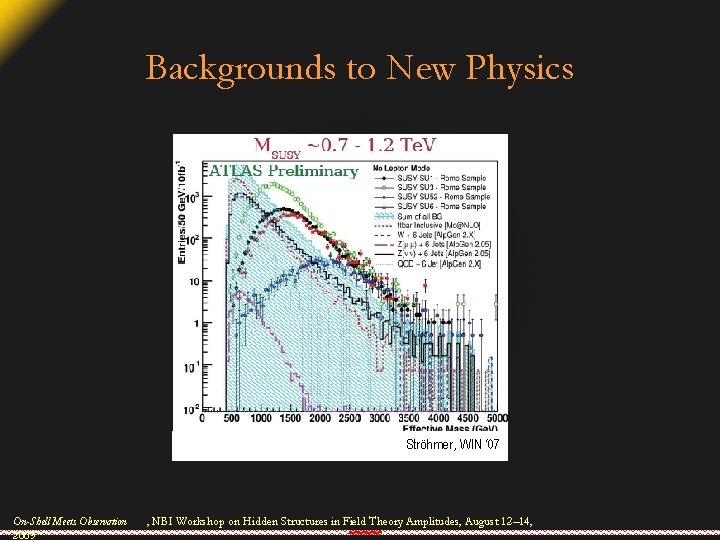
Backgrounds to New Physics Ströhmer, WIN ‘ 07 On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Ingredients for NLO • Leading-order contributions: tree-level • Real-emission contributions: tree-level with one more parton • Virtual corrections: one-loop amplitude 2 On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Ingredients for NLO Calculations • Tree-level matrix elements for LO and real-emission terms known since ’ 80 s Singular (soft & collinear) behavior of tree-level amplitudes, integrals, initial-state collinear behavior known since ’ 90 s • NLO parton distributions known since ’ 90 s • General framework for numerical programs known since ’ 90 s • Catani, Seymour (1996) [Giele, Glover, DAK (1993); Frixione, Kunszt, Signer (1995)] • Automating it for general processes Gleisberg, Krauss; Seymour, Tevlin; Hasegawa, Moch, Uwer; Frederix, Gehrmann, Greiner (2008) Bottleneck: one-loop amplitudes • W+2 jets (MCFM) W+3 jets • 2 Bern, Dixon, DAK, Weinzierl (1997– 8); Campbell, Glover, Miller (1997) On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

One-Loop Amplitudes • From the point of view of the final user , want Accurate and reliable codes – Many processes – Several suppliers, to cross-check results – Easy integration into existing tools (MCFM, SHERPA, ALPGEN, HELAC PYTHIA, …) – On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Traditional Approach • Feynman diagrams • Tensor loop integrals • Tensor reductions (Brown–Feynman, Passarino–Veltman) • Loop integral reductions (Melrose) • Huge intermediate expressions On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Why Feynman Diagrams Won’t Get You There Huge number of diagrams in calculations of interest — factorial growth • 2 → 6 jets: 34300 tree diagrams, ~ 2. 5 ∙ 107 terms ~2. 9 ∙ 106 1 -loop diagrams, ~ 1. 9 ∙ 1010 terms • But answers often turn out to be very simple • Vertices and propagators involve gauge-variant off-shell states • Each diagram is not gauge invariant — huge cancellations of gauge-noninvariant, redundant, parts in the sum over diagrams Simple results should have a simple derivation — Feynman (attr) • Is there an approach in terms of physical states only? • On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Focus on Amplitudes Differential cross sections • Use helicities, replace momenta by spinors • Use spinor notation On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

New Technologies: On-Shell Methods Use only information from physical states • Use properties of amplitudes as calculational tools • Factorization → on-shell recursion relations – Unitarity → unitarity method – Underlying field theory → integral basis – • Known integral basis: Formalism Unitarity On-Shell Meets Observation 2009 On-shell Recursion; D-dimensional unitarity via ∫ mass , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Unitarity: Prehistory • General property of scattering amplitudes in field theories • Understood in ’ 60 s at the level of single diagrams in terms of Cutkosky rules obtain absorptive part of a one-loop diagram by integrating tree diagrams over phase space – obtain dispersive part by doing a dispersion integral – In principle, could be used as a tool for computing 2 → 2 processes • No understanding • of how to do processes with more channels – of how to handle massless particles – of how to combine it with field theory: false gods of S-matrix theory – On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Unitarity as a Practical Tool Bern, Dixon, Dunbar, & DAK (1994) Key idea: sew amplitudes not diagrams • Compute cuts in a set of channels • Compute required tree amplitudes – Reconstruct corresponding Feynman integrals – Perform algebra to identify coefficients of master integrals – • Assemble the answer, merging results from different channels On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

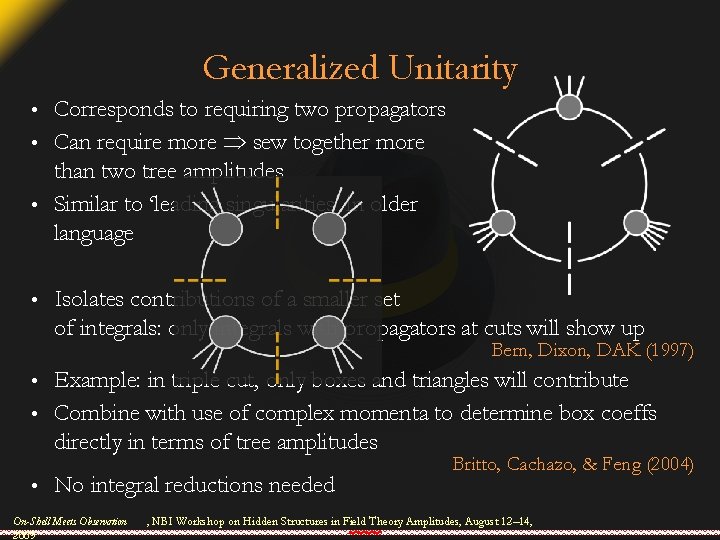
Generalized Unitarity Corresponds to requiring two propagators • Can require more sew together more than two tree amplitudes • Similar to ‘leading singularities’ in older language • • Isolates contributions of a smaller set of integrals: only integrals with propagators at cuts will show up Bern, Dixon, DAK (1997) Example: in triple cut, only boxes and triangles will contribute • Combine with use of complex momenta to determine box coeffs directly in terms of tree amplitudes • • No integral reductions needed On-Shell Meets Observation 2009 Britto, Cachazo, & Feng (2004) , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Remaining Integrals • In QCD, we also need triangle and bubble integrals Triangle coefficients can be extracted from triple cuts • But boxes have triple cuts too need to isolate triangle from them • Subtract box integrands (Ossola, Papadopoulos, Pittau) – Isolate using different analytic behavior (Forde) – Spinor residue extraction (Britto, Feng, Mastrolia) – On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

“One of the most remarkable discoveries in elementary particle physics has been the existence of the complex plane” On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

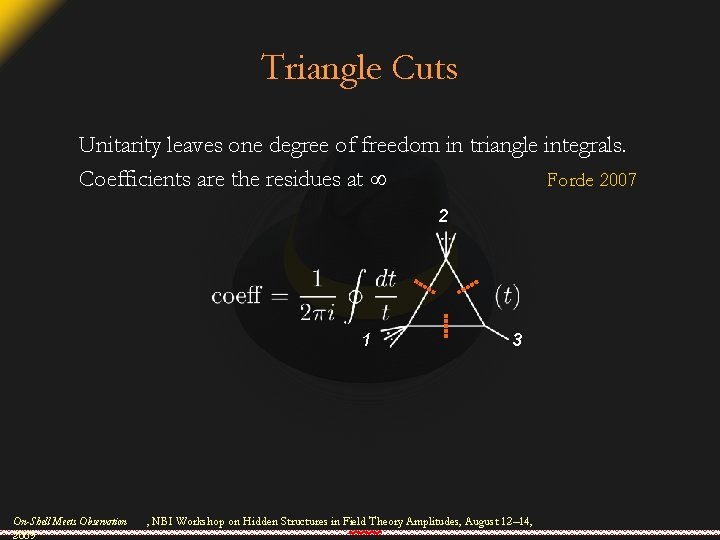
Triangle Cuts Unitarity leaves one degree of freedom in triangle integrals. Coefficients are the residues at Forde 2007 2 1 On-Shell Meets Observation 2009 3 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Direct Rational Contributions Badger (2008) • Replace D-dimensional components of gluon by massive scalar, integrate over scalar’s mass • Careful parametrization of loop momentum isolates rational coefficient as high-power behavior of integrand in the scalar mass, or via pole at On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

A Contour Integral Consider the contour integral Determine A(0) in terms of other residues On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

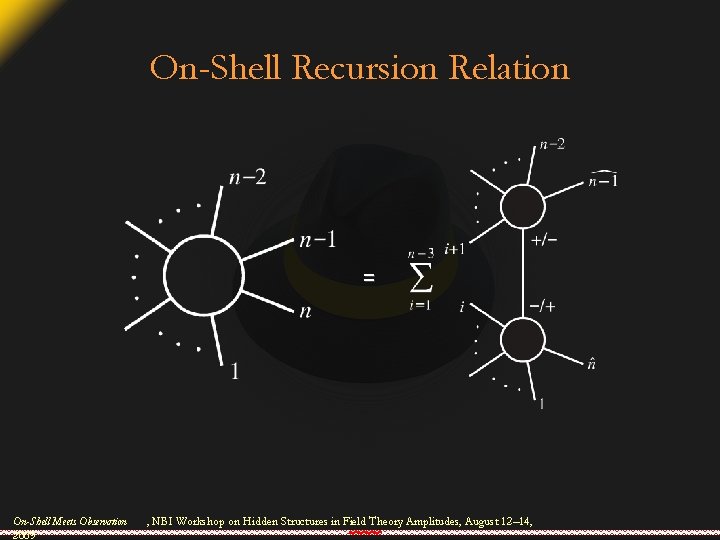
On-Shell Recursion Relation = On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Rational Terms Britto, Cachazo, Feng, & Witten; Bern, Dixon, DAK (2005) • Consider contour integral Spurious singularities If there’s a surface term, use auxiliary recursion On-shell recursion On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Computational Complexity Basic object: color-ordered helicity amplitude • Differential cross section needs sum over color orderings and helicities • Use phase-space symmetry to reduce sum over color orderings to polynomial number (or do sum by Monte Carlo) – Sum over helicities by Monte Carlo – • What is the complexity of a helicity amplitude? C exp n vs C np Asymptotically, only overall behavior really matters – We’re interested in moderate n – Brute-force calculations have huge prefactors as well as exp or worse behavior – • Want polynomial behavior – • Purely analytic answers for generic helicities are exponential Require a (partly) numerical approach for maximal commonsubexpression elimination, with analytic building blocks (e. g. ∫s) On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

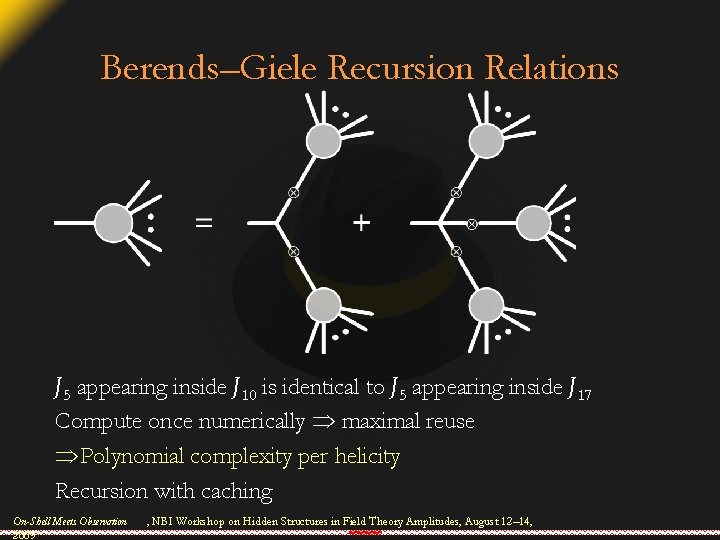
Berends–Giele Recursion Relations J 5 appearing inside J 10 is identical to J 5 appearing inside J 17 Compute once numerically maximal reuse Polynomial complexity per helicity Recursion with caching On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Aaron Bacall “Rather than learning how to solve that, shouldn’t I be learning how to write software that can solve that? ” On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Intelligent Automation • To date: bespoke calculations Need industrialization automation • Easiest to do this numerically • Numerical approach overall: worry about numerical stability • Do analysis analytically • Do algebra numerically • Only the unitarity method combined with a numerically recursive approach for the cut trees can yield a polynomial-complexity calculation at loop level • On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Black. Hat Carola Berger (MIT), Z. Bern, L. Dixon, Fernando Febres Cordero (UCLA), Darren Forde (SLAC), Harald Ita (UCLA), DAK, Daniel Maître (SLAC→Durham); Tanju Gleisberg (SLAC) • Written in C++ • Framework for automated one-loop calculations Organization in terms of integral basis (boxes, triangles, bubbles) – Assembly of different contributions – Library of functions (spinor products, integrals, residue extraction) • Tree amplitudes (ingredients) • Caching • Thus far: implemented gluon amplitudes; V + one/two quark pairs + gluon amplitudes • On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Other groups pursuing complementary lines of attack for numerical calculations within the unitarity framework: Ossola, Papadopoulos, Pittau, Mastrolia, Draggiotis, Garzelli, van Hameren Ellis, Giele, Kunszt, et al. Anastasiou, Britto, Feng, Mastrolia • Internal masses: Britto, Feng, Mastrolia; Ellis, Giele, Kunszt, et al. ; Badger • On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Numerical Stability • Usually ordinary double precision is sufficient for stability • Detect instabilities dynamically, event by event Check correctness of 1/ε coefficient • Check cancellation of spurious singularities in bubble coefficients • • For exceptional points (1 -2%), use quad precision On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

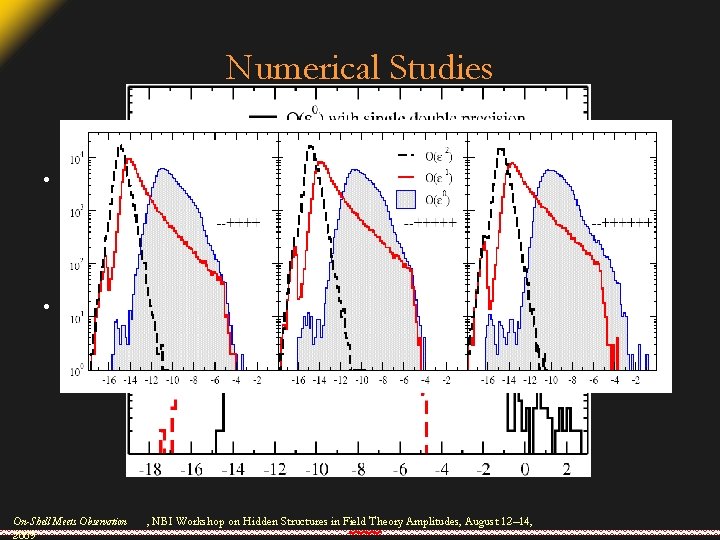
Numerical Studies • Check MHV amplitudes (− −++…+), against all-n analytic expressions; check other six-point amplitudes against highprecision values • Check W + 3 jet amplitudes against ultra high-precision values On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

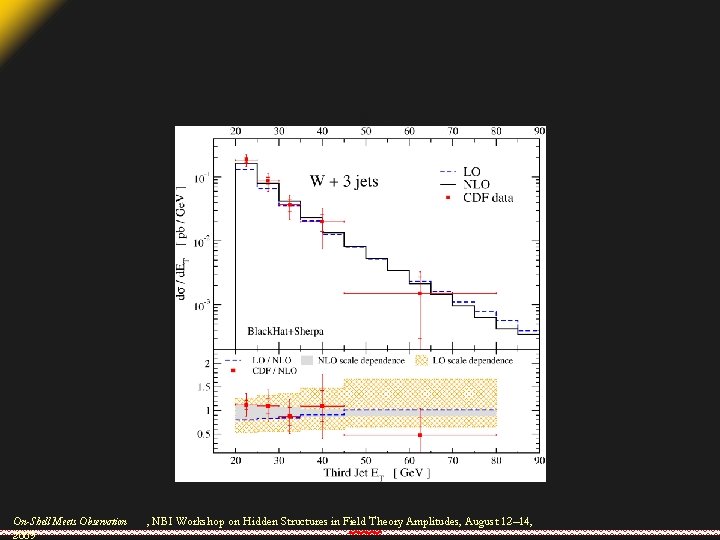
• To compute a physical cross-section, also need real-emission contributions – subtraction terms – Integration over phase space – Analysis package – Use SHERPA for these • Standard CDF jet cuts • SIScone (Salam & Soyez), with R = 0. 4 On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

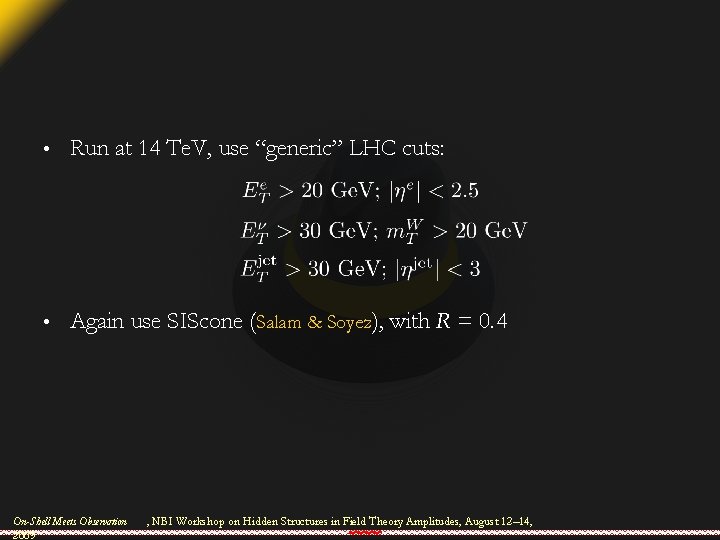
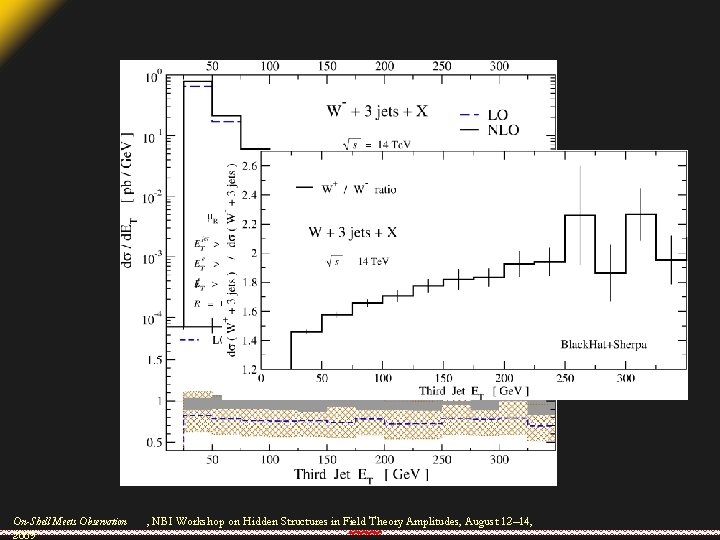
• Run at 14 Te. V, use “generic” LHC cuts: • Again use SIScone (Salam & Soyez), with R = 0. 4 On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

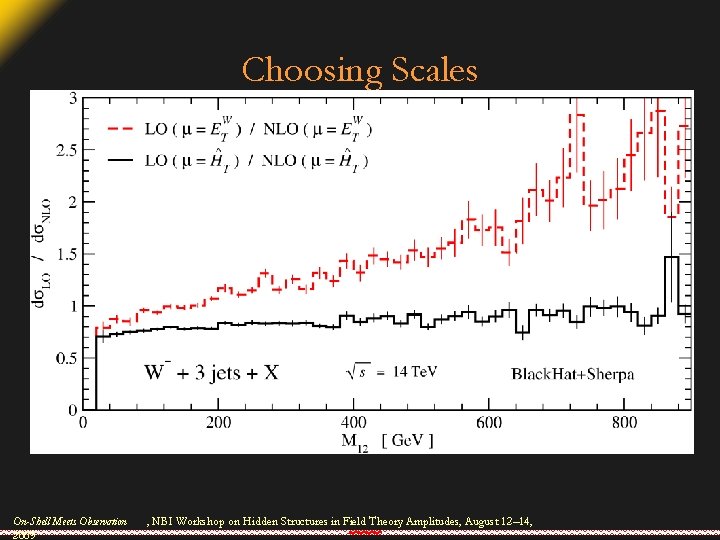
Choosing Scales • More important for LO calculations than NLO • Can affect shapes of distributions! • No perfect solution in processes with high jet multiplicity • Total partonic transverse energy appears to be a good choice, ETW isn’t On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

W Polarization • Polarization of low-p T Ws is well-known dilution in chargedlepton rapidity distribution asymmetry at Tevatron • Ws also appear to be polarized at high p T ET dependence of e +/e − ratio and missing ET in W +/W − • Useful for distinguishing “prompt” Ws from daughter Ws in top decay? On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

Summary • It’s been a long road, but an entirely new approach to amplitude calculations — on-shell methods — has made contact with experimental data • It promises to deliver important theoretical support for the LHC experimental program • Future insights and enhancements will have a role to play too! On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,

On-Shell Meets Observation 2009 , NBI Workshop on Hidden Structures in Field Theory Amplitudes, August 12– 14,