Online Class ANIMAL GENETICS BREEDING UNIT II Principles

Online Class ANIMAL GENETICS & BREEDING UNIT – II Principles of Animal & Population Genetics Lecture – 3 Quantitative Genetics: Components of Variance Dr K G Mandal Department of Animal Genetics & Breeding Bihar Veterinary College, Patna Bihar Animal Sciences University, Patna

Qualitative vs. Quantitative Genetics 1. Qualitative Genetics is the study of inheritance of those characters which are qualitative in nature. 2. Qualitative characters follow discontinuous variation 1. Quantitative Genetics is the study of inheritance of those difference between individuals which are of degree rather than kind, quantitative rather than qualitative. 2. Quantitative characters follow continuous variation.

3. Inheritance of qualitative characters is controlled by one, two or a very few number of genes. 3. Inheritance of quantitative characters is controlled by a large number of genes called polygenes, hence character are called polygenic traits. 4. Effect of individual gene is so prominent that its presence can be visible in the trait, for which those genes are called major gene. 4. Effect of individual gene is very small and not appreciable. cumulative effect of all the genes exhibits in the character, for which the polygenes are also called minor genes.

5. Qualitative traits can not be measured. 5. 6. Qualitative traits can be analysed through chisquare test only. 6. Quantitative traits are analysed through statistical tools, like mean, variance, SD, SE, correlation, regression, ANOVA etc. Quantitative traits can be measured/quantified through metric units (Kg. , ml, mm, cm, ltr, etc. ) for which they are also known as quantitative traits/biometric traits.

7. The classical mendelian phenotypic ratios can be seen between groups due to effect of a single gene difference at a given locus. 8. Does not influence by environment. 7. Classical medallion phenotypic ratios can not be seen. 8. Influenced through the effect of environment.

Qualitative vs Quantitative Genetics v v v v Measurement of characters No. of genes involved Effect of genes Types of variation Distribution Causes of variation Method of analysis : Biometric or non-biometric. : One, Two or Polygene : Major or Minor : Continuous or discontinuous : Normal or Binominal. : Genetic or environment or both : chi-square/Mean, SE, SD, Correlation, regression, ANOVA.

Values and Means P=G+E Where, P = Phenotypic value G = Genotypic value E = Environmental deviation Value assigned to the genotypes A 2 A 2 A 1 A 1 -a 0 d +a

Population Mean For a single locus M = a(p - q) + 2 pqd M = population mean a = assigned genotype value of homozygotes. d = degree of dominance assigned to heterozygote. if d = 0, then M = a (1 – 2 q) if d = a, then M = a (1 – 2 q 2) if A 1 is fixed (p = 1), then M = a if A 2 is fixed (q = 1), then M = -a

Since, quantitative traits are influenced by the genes situated at many loci then, M = ∑a(p – q) + 2∑pqd. If all the genes that increase the value are fixed, then population mean, M = +∑a and vice versa , (M = -∑a).

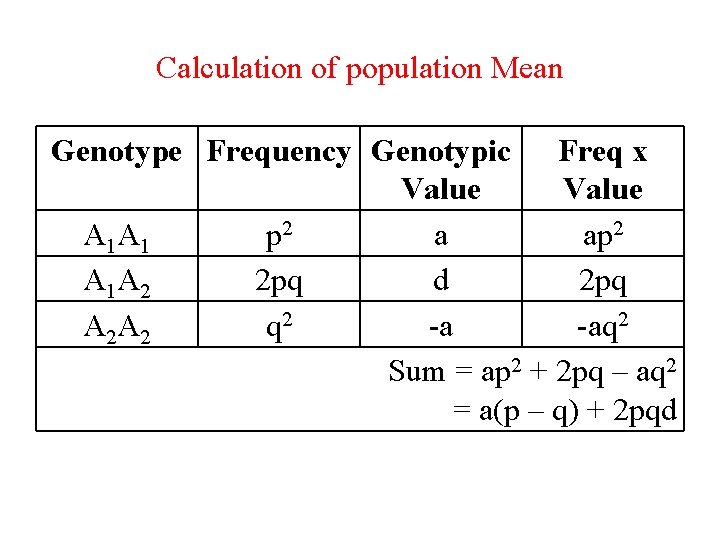
Calculation of population Mean Genotype Frequency Genotypic Freq x Value A 1 A 1 p 2 a ap 2 A 1 A 2 2 pq d 2 pq A 2 A 2 q 2 -a -aq 2 Sum = ap 2 + 2 pq – aq 2 = a(p – q) + 2 pqd

Genotypic value It is measured as a deviation from the population mean Genotype Assigned Values GV deviated from population mean A 1 A 1 a a – M= a – [(p – q) + 2 pqd] = 2 q ( a – pd) A 1 A 2 d A 2 A 2 -a d – M = d – [(p– q) + 2 pqd] = a (q – p) + d (1 – 2 pq) -a –M = -a – [(p – q) + 2 pqd] = -2 p (a +qd) Mean genotypic value = 0 (zero)

Average effect of Gene It is the mean deviation from the population mean of individuals which have received that gene from one parent the gene received from other parent having the at random from the population. Gene Frequency Average effect A 1 p X 1 A 2 q X 2 A 1 = A 1 Gene A 2 = Genotype Frequency Value GV A 1 p a ap A 1 A 2 q d qd ______________________________ Mean GV of A 1 A 1 & A 1 A 2 = ap + qd The average effect of A 1 = X 1 = (ap+qd)-[a(p-q)+2 pqd] =ap+qd-a(p-q)-2 pqd =ap+qd-ap-aq-2 pqd =aq+qd-2 pqd =q[a+d-2 pd] =q[a+d(1 -2 p} =q[a+d(p+q-2 p)] =q[a+d(q-p)]

A 1=A 1 A 2 Gene A 2=A 2 A 2 Genotype Frequency Value GV A 1 A 2 p d pd A 2 q -a -aq _______________________________ Genotypic value of A 1 A 2 & A 2 A 2 = pd-aq Average effect of A 2=X 2 =-pd-aq -[a(p-q)+2 pqd] = pd- aq – ap +aq - 2 pqd = p[-a+d-2 qd] = -p[a-d(p+q-2 q)] = -p[a+d(q-p)] Thus, X 1 = q[a+d(q-p)] X 2 = -p[a+d(q-p)]

Average effect of gene in terms of gene substitution. Suppose, x=average effect of gene in terms of gene substitution & A 2 is substituted by A 1. Genotype Freq. Amount of change Thus, A 1 A 2 A 1 A 1 p(a-d) d a p Amount of change = p(a-d) A 2 A 2 A 1 A 2 Freq. -a d q q(d-(-a)) =q(d+a) Overall change in mean genotypic value = p(a-d)+q(d+a) = ap-pd+qd+aq = a(P+q)+qd-pd = a+d(q-p) Thus, X 1=q. X X 2=q. X

Breeding Value v Breeding value is the value associated with the genes carried by an individual. v Breeding value can also be judged by the mean phenotypic value of its progeny. v If an individual is mated to a number of individuals taken at random from the population, then its breeding value is twice the mean deviation from the population mean. v In terms of average effect of gene, the breeding value of an individual is equal to sum of the average effect of genes it carries, the summation being made over the pair of alleles at each locus and over all loci.

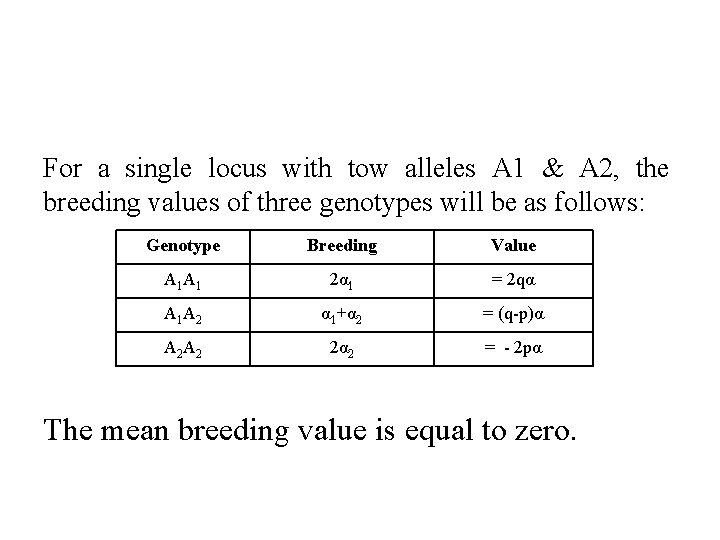
For a single locus with tow alleles A 1 & A 2, the breeding values of three genotypes will be as follows: Genotype Breeding Value A 1 2α 1 = 2 qα A 1 A 2 α 1+α 2 = (q-p)α A 2 2α 2 = - 2 pα The mean breeding value is equal to zero.

Components of variance v Population mean gives no idea about the phenotypic value recorded on different individuals. v Measures of dispersion tells about scaterness of the observations in a set of data. v Variance is an important components of measures of dispersion because of its two important properties: § Additivity § Sub divisibility

When values are expressed as deviation from the population mean, the mean of the squared deviation is known as variance (s 2) = 1/N ∑(xi-x)2 Where, x = population mean xi = x 1, x 2, x 3, ……………x. N Variance can be sub divided or partitioned into different components according to different causes of variation.

Phenotypic value of an individual depends on its genotypic value and environment in which it is subjected as well as interaction between genotype and phenotype. Thus, P=G+E P 2 = (G + E)2 = G 2 +E 2 +2 GE Where, P = Phenotypic value, G = Genotypic value, E = Environmental deviation. Since, all values are taken as deviation from the population mean, then VP=VG+VE+2 COVGE In absence of interaction between genotype and environment, VP=VG+VE

Genotypic value, depends on breeding value, dominance deviation and gene interaction, then G=A+D+I To find out important causes of genetic variation the genotypic variance is to be partitioned according to different causes of variation, i. e. VG = VA+ VD+VI There are two different kinds of environmental factors which may influence phenotype, they are: 1. General environmental variance, VEg 2. Special environmental variance, VEs Hence, VE = Veg + VEs Thus, VP=VG+VE =VA+VD+VI+VEg+VEs

Importance of variance & its components v Variance can be partitioned into different components corresponding to its causing factors. v Partitioning of variance is useful to know the effect of different factors causing the variation in the character. v To estimate the percent contribution of different causing factors to the total phenotypic variance. v To estimate the relative importance of different causing factors as a proportion of the total phenotypic variance.