Online Ascending Auctions for Gradually Expiring Items Ron

Online Ascending Auctions for Gradually Expiring Items Ron Lavi SISL/IST, Caltech and Noam Nisan Hebrew University

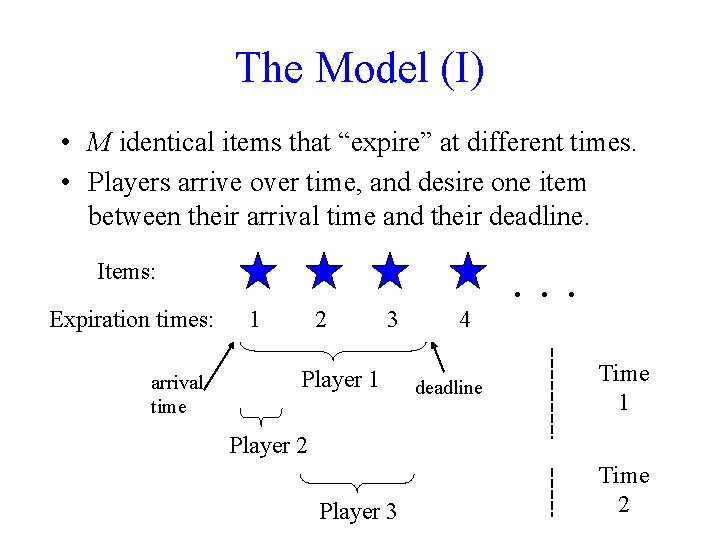
The Model (I) • M identical items that “expire” at different times. • Players arrive over time, and desire one item between their arrival time and their deadline. Items: Expiration times: arrival time 1 2 3 Player 1 4 deadline . . . Time 1 Player 2 Player 3 Time 2

The Model (II) • Player i has value vi for receiving a desired item. • Players are selfish: – All information (arrival time, deadline, value) is private, known only to the player. – Each player acts in order to maximize his own utility: value - price. • Our goal is to maximize the sum of (true) values of players that receive an item (the “social welfare”). • Applications: – In economic settings e. g. transportation tickets – In computational settings e. g. bandwidth allocation

Algorithmic Status • Well studied - equivalent to scheduling of unit jobs. • Offline optimal allocation is poly-time computable (has a matroid structure). • Lower bound of 1. 618 for online approximation. [Hajek] • Online greedy is a 2 - approximation: greedy: at time t, allocate item t to the player with highest value. – This assumes obedient players that simply reveal their private information.

Truthfulness and its difficulties • A popular approach: truthful auctions. – Motivating the player to reveal his true parameters. – Strong argument of dominant strategy: no matter what others do, the truth will maximize “my” utility. – Many recent positive examples for truthful auctions. • Unfortunately, we show that: Theorem: Any deterministic truthful auction for our allocation problem cannot obtain an approximation ratio better than M. – A simple truthful M - approximation exists.

How to approach this difficulty? • Relax the equilibrium notion to Bayesian - Nash: – Not a worst-case analysis. Requires strong distributional assumptions. • Add assumptions about player types. E. g. assume values in [vmin , vmax]. Then a randomized truthful 2 log(vmax - vmin) approximation exists (a special case of [BSZ]). – vs. a deterministic 2 - approximation without any assumptions when truthfulness is dropped. • Our approach: – New, relaxed, notion of equilibrium. – Worst - case analysis. No distributional assumptions. – No additional assumptions about player types.

Outline for rest of the talk • Describe two ascending auctions: – Their algorithmic properties – Intuition to an equilibrium notion that fits well • Describe a new notion of equilibrium – discuss its properties • Main theorem – Intuition for the proof

The Online Iterative Auction • Maintain temporary prices and owners for each item (initialized to 0). • At each time unit t=1, 2… : • Repeat: Some player that doesn’t currently own an item temporarily takes an item, and increases the price by . Until no losing player wishes to make a new bid. • Allocate item t to its current owner for the listed price - . Keep prices and temporary owners for next time unit. • This is an adaptation of the Iterative Auction of [DGS].

Example Temp. price 0 0 Temp. winner -- -- 1 2 Item Player I: v=3, d=2 Player II: v=5, d=2 Player III: v=2, d=1 =1

Example Temp. price 1 0 =1 Temp. winner I -- (phase 1) 1 2 Item Player I: v=3, d=2 Player II: v=5, d=2 Player III: v=2, d=1

Example Temp. price 1 1 =1 Temp. winner I II (phase 2) 1 2 Item Player I: v=3, d=2 Player II: v=5, d=2 Player III: v=2, d=1

Example Temp. price 2 1 =1 Temp. winner III II (phase 3) 1 2 Item Player I: v=3, d=2 Player II: v=5, d=2 Player III: v=2, d=1

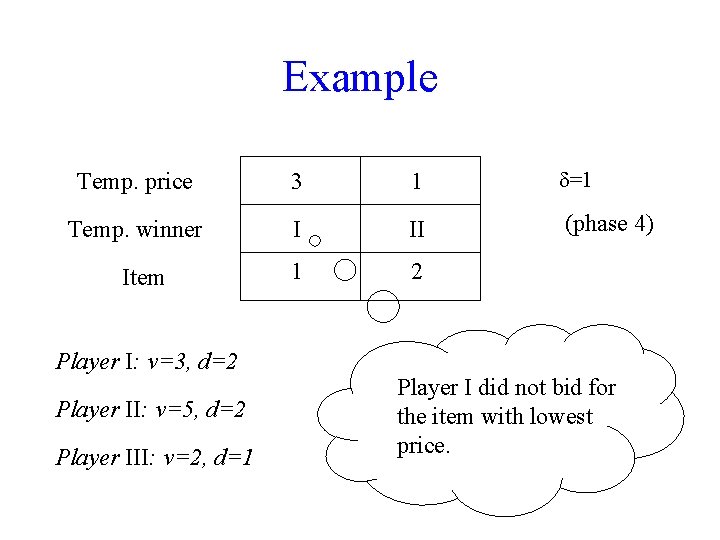
Example Temp. price 3 1 =1 Temp. winner I II (phase 4) 1 2 Item Player I: v=3, d=2 Player II: v=5, d=2 Player III: v=2, d=1

Example Temp. price 3 1 =1 Temp. winner I II (phase 4) 1 2 Item Player I: v=3, d=2 Player II: v=5, d=2 Player III: v=2, d=1 Player I did not bid for the item with lowest price.

Example Temp. price 3 1 Temp. winner I II 1 2 Item =1 Result: Player I: v=3, d=2 Player I wins item 1 and pays 2. Player II: v=5, d=2 If no new player will arrive, player II will win item 2 for a price of 0. Player III: v=2, d=1 But, player II might not win at all if a new high valued player will now arrive.

Players’ behaviors (the offline case) DFN([DGS]): A player is myopic if he always bids on the item with lowest price among those he desires. THM([DGS], [GS]): Assume all players arrive at time 1: • When all players are myopic then the online iterative auction finds the optimal allocation*. • When all other players are myopic, player i will maximize* his utility by behaving myopically. * up to a difference of about .

Basic structure of allocations S = the optimal allocation j’’ 1 2 j’ j . . . d M • A tight block B S: |B|=d and j B d(j) < d. • Tight blocks must be prefixes of S, thus contained one in the other. • Special focus in the minimal tight block f.

Basic structure of allocations f j’’ 1 2 S = the optimal allocation j’ j . . . d M i* Highest un-allocated player determines VCG price of all players in f • A tight block B S: |B|=d and j B d(j) < d. • Tight blocks must be prefixes of S, thus contained one in the other. • Special focus in the minimal tight block f. • Every j in f can be located first. • Therefore, its “social cost” is the value of the highest unallocated player.

The offline iterative auction with myopic players finds the optimal allocation f j’’ 1 2 S = the optimal allocation j’ j . . . d M i* Highest un-allocated player determines VCG price of all players in f • All prices in f are equal (because of the structure of swaps): – p(j’) < p(j’’) since j’ is myopic – p(j’’) < p(j’) since j’’ is myopic and has far-enough deadline. • Prices will continue to go up exactly until v(i*).

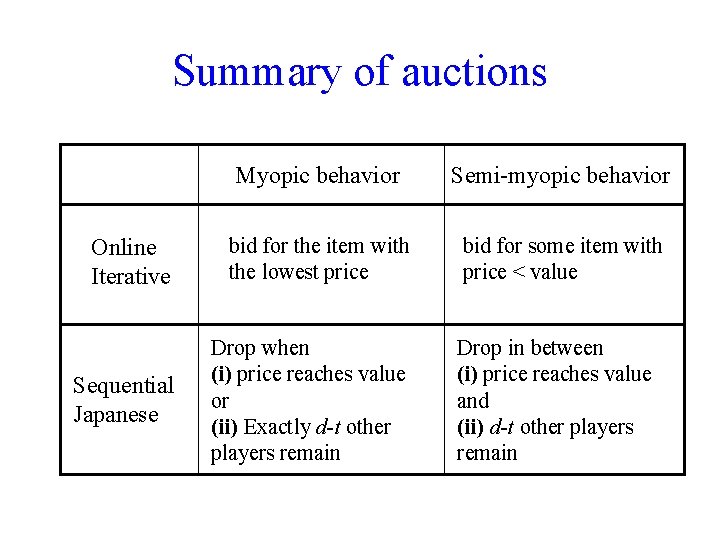
Players’ behaviors (the online case) • In the online case, non myopic behaviors might perform better. • E. g. bidding more aggressively for the current item makes sense if one anticipates that many competitive players will arrive later on. DFN: A player is semi - myopic if he bids on some item with price lower than his value. THM: If all players are semi - myopic then the online iterative auction obtains a 3 - approximation.

The Sequential Japanese Auction • Item t is sold at time t using a classic Japanese auction: – The auctioneer starts raising a price. – Each player decides whether to drop or to stay as the price ascends. – We allow to observe how many players remain at each moment. – The price halts when only one player remains. This player wins and pays the price that was reached (up to some tie breaking adjustment rule).

Example Player I: v=3, d=2 Player II: v=5, d=2 What if players I and II decide not to participate at all in the auction for item 1? Player III: v=2, d=1 Player III will win item 1. Player I will certainly not win anything. Player II might win item 2, but for a price of 3.

Example continued Player I: v=3, d=2 Player II: v=5, d=2 Player III: v=2, d=1 Suppose players I and II decide to stay until the price reaches their value, or until there remain two players in the auction (including themselves): At price=2, player III will drop. 2 Immediately afterwards, both I and II drops. So either I or II wins and pays 2. Price

Players’ behaviors (the offline case) Surprisingly, a notion of myopic behavior leads to the optimal allocation here as well: DFN: A player is myopic if, at any time t, he drops exactly: – when the price reaches his value, or – when d - t other players remain (where d is his deadline). THM: If all players arrive at time 1, and are all myopic, then the Sequential Japanese Auction finds the optimal allocation.

Proof • p*=value of highest unallocated player i*, |f|=d • Price < p* implies that no one from f drops: – At least d+1 players still remain (all f + i*) – Price is still low. • At price = p* all remaining unallocated players drop, and after them all remaining players of S. • Players of f start to drop only after all others have dropped. • winner of item 1 = optimal item 1 winner. • Continue inductively. p* Price

Players’ behaviors (the online case) • In the online case, again, bidding more aggressively for the current item makes sense if one anticipates that many competitive players will arrive later on. DFN: A player is semi - myopic if, at any time t, he drops: – not earlier than d-t other players remain, and – not later than when the price reaches his value. THM: If all players are semi - myopic then the Sequential Japanese Auction obtains a 3 approximation.

Summary of auctions Myopic behavior Semi-myopic behavior Online Iterative bid for the item with the lowest price bid for some item with price < value Sequential Japanese Drop when (i) price reaches value or (ii) Exactly d-t other players remain Drop in between (i) price reaches value and (ii) d-t other players remain

Proving the approximation Semi - Myopic Algorithms Greedy Myopic Allocate to bidder with highest value Semi - myopic Allocate according to current best allocation Allocate to someone with value > value of the winner of item t in a current best allocation ( = an optimal allocation of items t, …, M among the active players at time t ). Lemma: Any semi - myopic algorithm obtains a 3 - approximation. Lemma: When players are semi - myopic then both our auctions are semi - myopic algorithms.

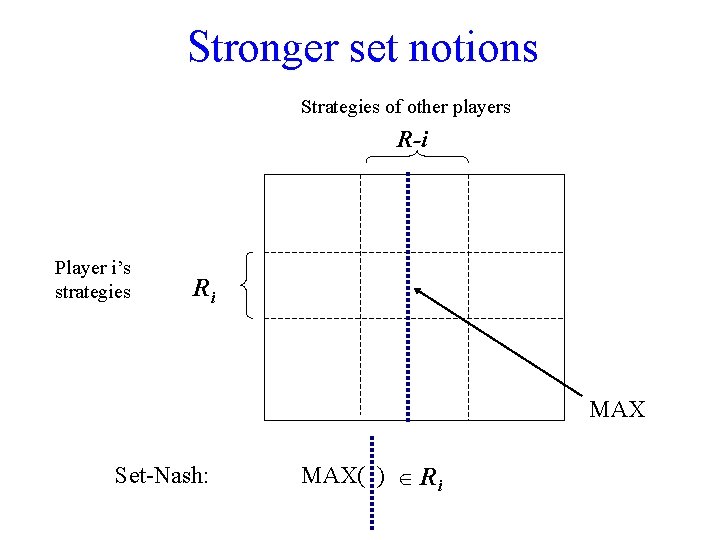
Set - Nash Equilibrium • The above intuition implies that we do not expect a player to follow a specific strategy. Instead, we define a set of “recommended strategies” Ri for player i. DFN: The strategy sets R 1 … Rn are in Set – Nash equilibrium if a best response to every s-i R-i exists in Ri • Comment 1: If | Ri |=1, then equivalent to regular Nash. • Comment 2: Best response to mixed strategies might be outside Ri – stronger definitions can require that too. • Comment 3: Only interesting if you can say something about the outcome when everyone plays in Ri • Comment 4: Naturally generalizes to games with incomplete information without a Bayesian prior: Ri(ti)

Stronger set notions Strategies of other players R-i Player i’s strategies Ri Set domination: > (coordinate-wise)

Stronger set notions Strategies of other players R-i Player i’s strategies Ri Set mixed Nash: E π( ) > E π( )

Stronger set notions Strategies of other players R-i Player i’s strategies Ri MAX Set-Nash: MAX( ) Ri

Main Theorem: The Online Iterative Auction and the Sequential Japanese Auction Set - Nash implement a 3 - approximation of the welfare. I. e. , both auctions have Set - Nash equilibrium that are all semi - myopic, hence guarantee a 3 - approximation. • All the recommended strategies are not dominated. • The recommended strategies contain best responses even if the strategies of the others are from a much larger set. • The recommended strategies do not necessarily contain b. r. to mixed recommended strategies -- We think this is an interesting open problem.

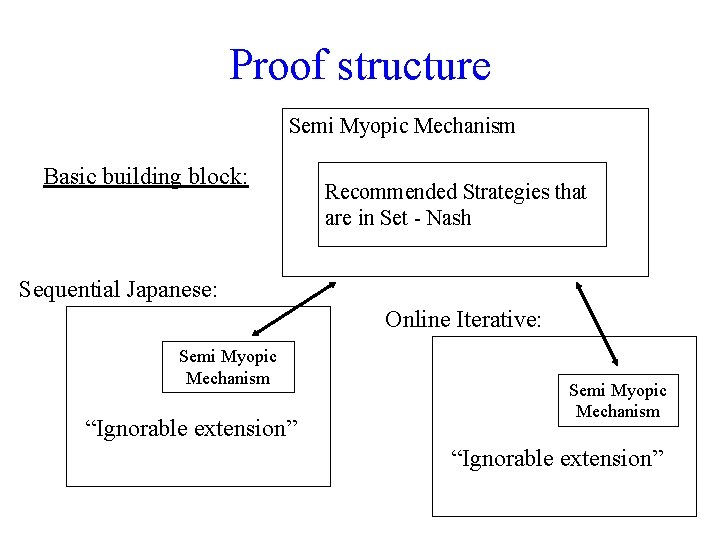
Proof structure Semi Myopic Mechanism Basic building block: Recommended Strategies that are in Set - Nash Sequential Japanese: Online Iterative: Semi Myopic Mechanism “Ignorable extension”

Reminder: basic structure of allocations ft j j’ t St = the optimal allocation t+1 . . . d M i* Highest un-allocated player determines VCG price of all players in ft Reminder: with myopic players, the ascending auctions compute ft and VCG prices

Semi Myopic Mechanisms Strategy space. Extended direct revelation: { arrival time, value, “false” deadline, “true” deadline } (Similar in spirit to “ 2 nd chance mechanisms” [NR]) Allocation rule. Compute St according to “pretend deadlines”: “pretend deadline” = “false” deadline “true” deadline If this has not passed. Otherwise. – Allocate item t to some player in ft. Payment Rule. – For any player i, let ct(i) be his VCG price for entering St. ct(i) If i ft. – Set temporary prices pt(i) = [0, ct(i) ] If i St - ft. Otherwise – The winner i pays max p (i) 0 t’<t t’

Set - Nash in Semi Myopic Mechanisms Recommended strategies: declare true arrival time, value, and true “true deadline”, and any “false deadline” < true deadline. Lemma 1: When all players play recommended strategies then the allocation rule of a semi myopic mechanism is a semi myopic algorithm. Lemma 2: These recommended strategies form a Set Nash Equilibrium.

Semi Myopic Mechanism Ascending Auctions Recommended strategies for the Online Iterative Auction: play myopically with a fake deadline until it has passed, and myopically with the real deadline afterwards. Lemma: The Semi Myopic Mechanism is embedded in the Online Iterative Auction. Proof sketch: need to show that the requirements of the semimyopic mechanism hold: – winners belong to ft – prices are VCG Already know these from the offline analysis

Summary • We study an online setting with “gradually expiring items”. • We first saw that truthful auctions cannot perform well. • We then explored a new approach to this difficulty. – Worst case, no additional assumptions on players. • Analyzed two adaptations to classical ascending auctions. – Both obtain a 3 - approximation under a large family of selfish behaviors. • Introduced the notion of “Set - Nash equilibrium”. – Both our auctions have Set - Nash equilibrium that guarantees a 3 - approximation of the social welfare.