Onetotwo dimensional mapping of DFT Let so that

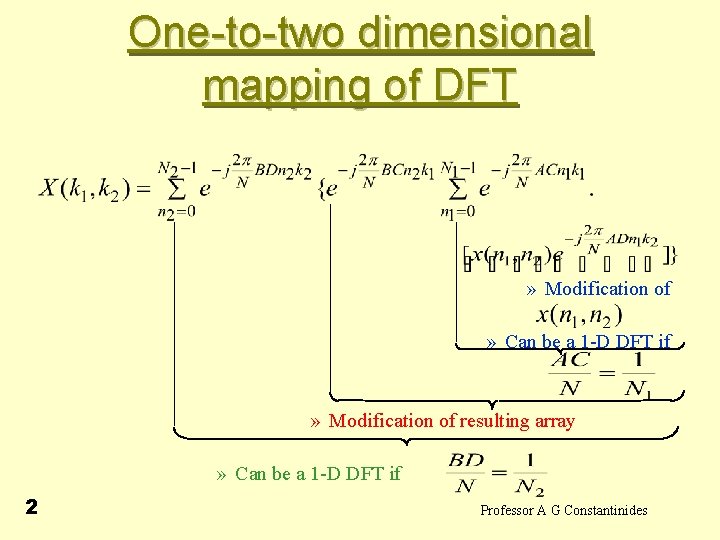
One-to-two dimensional mapping of DFT • Let • so that • and • • 1 Professor A G Constantinides

One-to-two dimensional mapping of DFT » Modification of » Can be a 1 -D DFT if » Modification of resulting array » Can be a 1 -D DFT if 2 Professor A G Constantinides

One-to-two dimensional mapping of DFT • Thus the conditions below must prevail • We identify 4 cases. • 1) When • 2) When 3 Professor A G Constantinides

One-to-two dimensional mapping of DFT • 3) When • 4) When 4 Professor A G Constantinides

One-to-two dimensional mapping of DFT • Since. • • And n must range from 0 to • and k must range from 0 to Only two cases are viable Case A and Case B 5 Professor A G Constantinides

One-to-two dimensional mapping of DFT. Twiddle factors Computational Complexity: 6 Inner DFT: Outer DFT: Twiddle factors: Total: Professor A G Constantinides

One-to-two dimensional mapping of DFT • Address mappings (Case A) 0 1 1 … • 0 1 2 3. . 7 . … … … Professor A G Constantinides

Good - Thomas mapping • Consider the index in the exponential of a DFT • For the elimination of cross terms and for proper DFTs we need: • Thus and hence • Similarly • All conditions w. r. t. 8 Professor A G Constantinides

Good - Thomas mapping • When such that • Euclid’s Algorithm there exist • … 9 Professor A G Constantinides

Euclid’s Algorithm (31, 11) • (1) 31=2 x 11+9 • (2) 11=1 x 9+2 • (3) 9=4 x 2+1 • 4 x(2) yields 4 x 11=4 x 9+4 x 2=4 x 9+(9 -1)=5 x 9 -1 • 5 x(1) yields 5 x 31=10 x 11+5 x 9=10 x 11+(4 x 11+1) Thus 5 x 31 -4 x 11=1 ie 10 Professor A G Constantinides

One-to-two dimensional mapping of DFT • The mapping from n to from as is obtained • Hence • and 11 Professor A G Constantinides

Euclid’s Algorithm • Given to show that • Assume and write • Now consider 12 • And reduce result is then the in some order Professor A G Constantinides

One-to-two dimensional mapping of DFT • For each residue of different, else we have , and for will be and • And hence divides r which is untrue as or divides which is also untrue as 13 Professor A G Constantinides

One-to-two dimensional mapping of DFT • Hence • Thus hence an n such that. But • Or • Since and follows that it is also true 14 and it Professor A G Constantinides

Prime Radix Algorithm • Finite duration signal • DFT • Set 15 so that Professor A G Constantinides

Prime Radix Algorithm • Computational Complexity • Reduction in complexity is achievable via segmented computations • ; for even N • 16 point DFTs Professor A G Constantinides

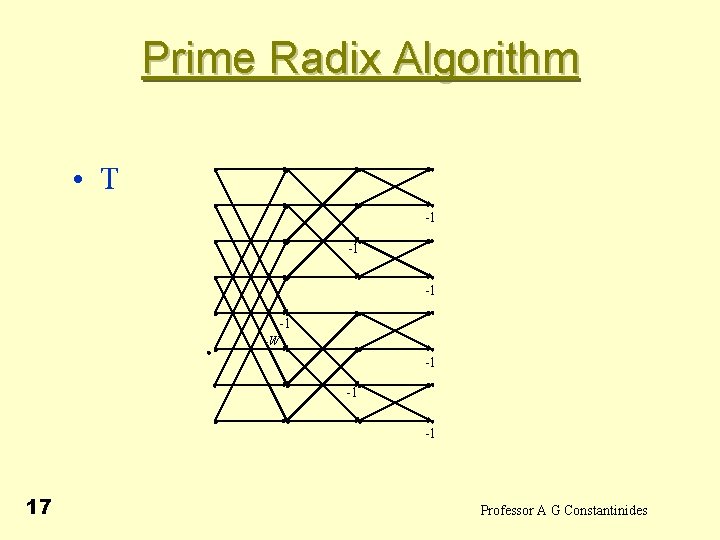
Prime Radix Algorithm • T -1 -1 -W -1 -1 -1 17 Professor A G Constantinides

Prime Radix Algorithm • May be regarded as 18 Professor A G Constantinides

Prime Radix Algorithm • Recall that and for any fixed with prime • is equal to a rearrangement of the integers 19 Professor A G Constantinides

Prime Radix Algorithm • Since • (i) and there are no common factors between n. k and P • (ii) For every multiple of P we have • It follows that all powers of W from 0 to P will exist in each but not in the same order. 20 Professor A G Constantinides

Prime Radix Algorithm • Thus for 21 Professor A G Constantinides

Prime Radix Algorithm 22 Professor A G Constantinides

Prime Radix Algorithm • • • 23 In general and where Note that in view of the Number Theoretic result we can also rearrange w. r. t. any number Q i. e. Reduce {n. k. Q} mod P Professor A G Constantinides

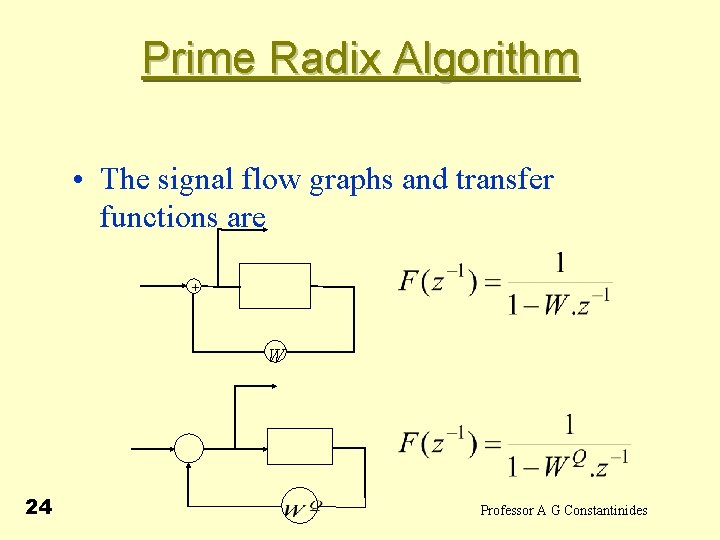
Prime Radix Algorithm • The signal flow graphs and transfer functions are + W 24 Professor A G Constantinides

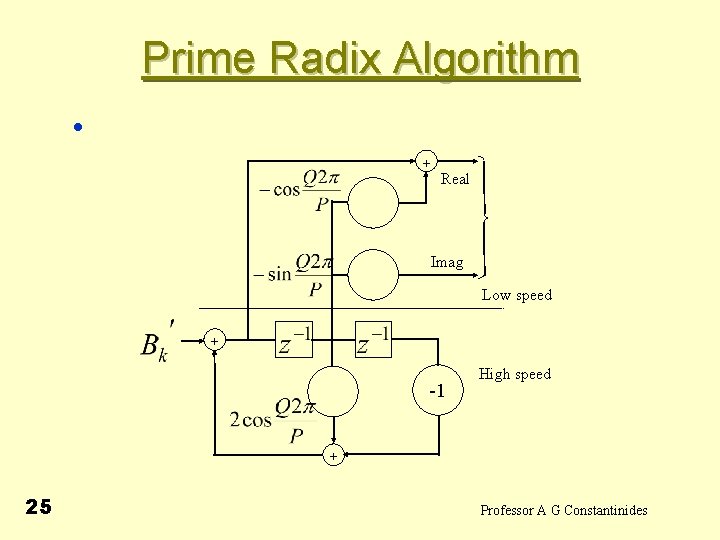
Prime Radix Algorithm • + Real Imag Low speed + -1 High speed + 25 Professor A G Constantinides

Prime Radix Algorithm • 26 P Q Cos(2πQ/P) 17 4 0. 0923 29 7 0. 05411 47 1 0. 9911 Shift/PROM Scaling Professor A G Constantinides

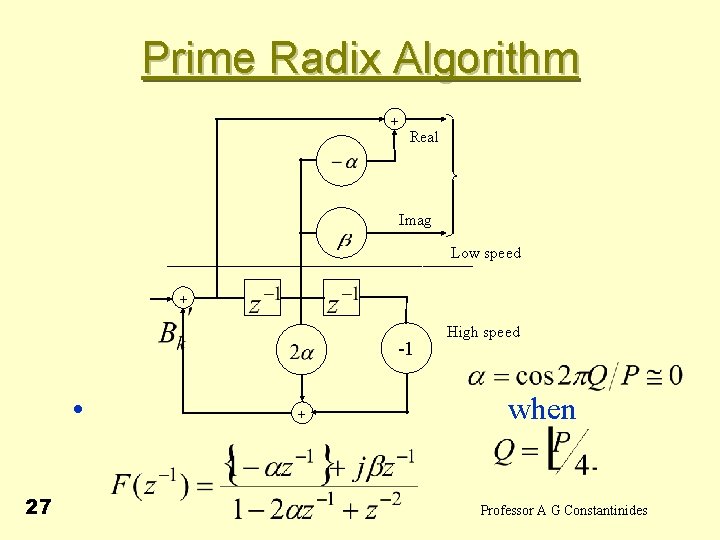
Prime Radix Algorithm + Real Imag Low speed + -1 • 27 + High speed when Professor A G Constantinides

Prime Radix Algorithm • Approximation is in the denominator where ideally • Actually 28 with small • Hence actual operation can be modified to improve performance towards ideal Professor A G Constantinides

Prime Radix Algorithm • Thus • hence • where 29 Professor A G Constantinides