OneHot State Machine Design 1 ECE 352 Digital

One-Hot State Machine Design 1 ECE 352 Digital System Fundamentals One-Hot State Machine Design

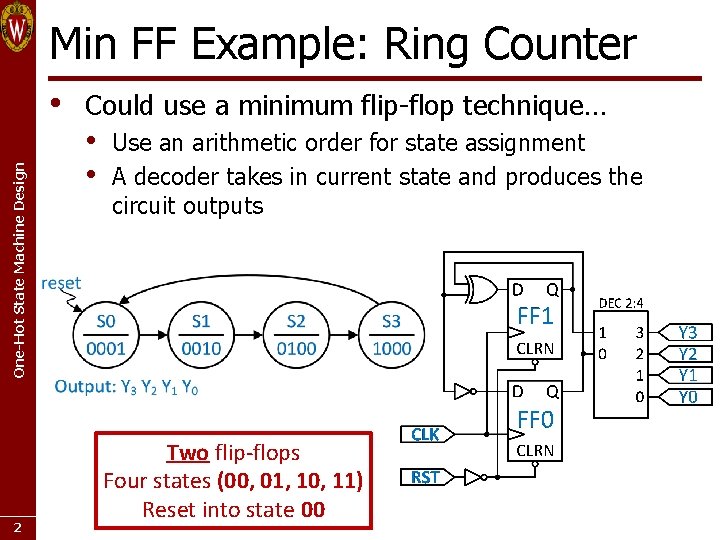
Min FF Example: Ring Counter One-Hot State Machine Design • 2 Could use a minimum flip-flop technique… • • Use an arithmetic order for state assignment A decoder takes in current state and produces the circuit outputs Two flip-flops Four states (00, 01, 10, 11) Reset into state 00

One-Hot State Machine Design One-Hot State Assignment 3 • • Alternative to minimum FF assignment If m states, use m flip-flops • • • The current state is defined by the flip-flop that contains a 1 (all others MUST contain 0) i. e. , “one” of the flip-flop outputs is “hot” (a “ 1”) This method is also called “one flip-flop per state” Conceptually, the “ 1” is a token passed from the current state to the next state In reality, a FF’s input logic will produce a 1 if and only if that FF is the next state

One-Hot State Machine Design Create Hardware From Diagram • Does not require a state table! • • One flip-flop per state Create an AND gate per incoming transition and OR these together to make FF input logic “What are all the ways this can be the next state? ” • • 4 Moore outputs: OR together outputs of FFs that represent states where the output is 1 Mealy: create an AND gate for each transition where the output is 1, and OR these together “What are all the ways this output can be 1? ”

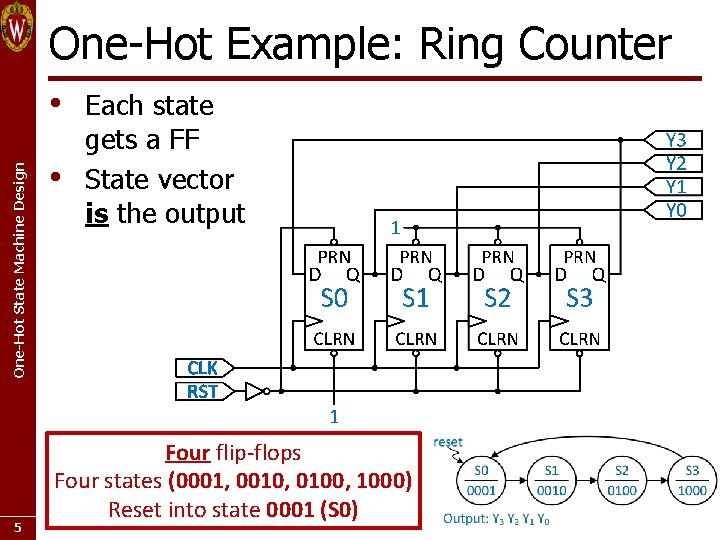
One-Hot Example: Ring Counter One-Hot State Machine Design • 5 • Each state gets a FF State vector is the output Four flip-flops Four states (0001, 0010, 0100, 1000) Reset into state 0001 (S 0)

One-Hot Reset State One-Hot State Machine Design • Remember, exactly one FF must contain a 1 at any moment • • The one that has a flip-flop with an output equal to 1 Which state is the next state? • The one that has a flip-flop with an input equal to 1 On a circuit reset, we need to load 1 into FF that represents the reset state, and 0 into the others • • 6 Which state is the current state? Use PRESET (SET) (“on reset, become 1”) for that FF Use CLEAR (RESET) (“on reset, become 0”) for others

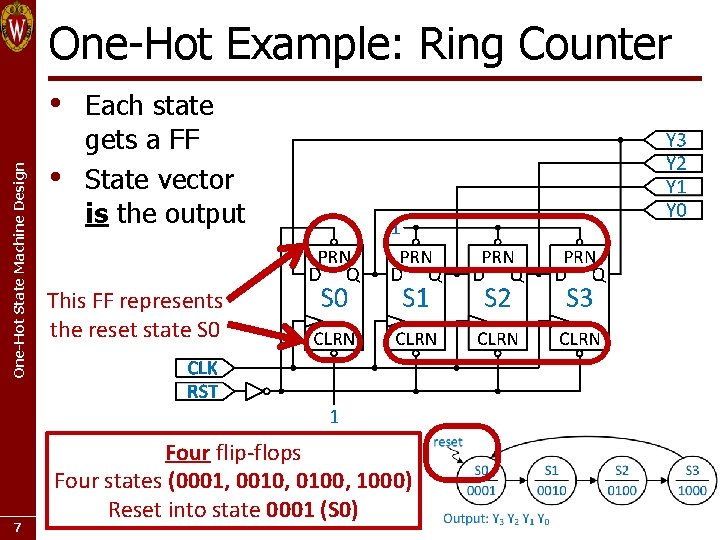
One-Hot Example: Ring Counter One-Hot State Machine Design • 7 • Each state gets a FF State vector is the output This FF represents the reset state S 0 Four flip-flops Four states (0001, 0010, 0100, 1000) Reset into state 0001 (S 0)

One-Hot Terminology & Naming One-Hot State Machine Design • 8 • Since we use one flip-flop per state, we may use the words “state” and “flip-flop” interchangeably If we say the current state is S 0, remember the “current state” is actually the complete state vector (all FF outputs, not just FF S 0’s output) • On the previous slide, the state vector for each state is that state’s output (e. g. , state S 0 is actually state 0001) • This means there a lot of “unused” states! • For state S 0 we created a flip-flop named S 0 • • • We might name its output S 0 (same as the FF) or Q 0 We might name its input D 0, S 0 NEXT, etc. Its input and output cannot both be called S 0…

Design Tradeoffs One-Hot State Machine Design • • Design Simplicity • Circuit Quality • • • 9 Usually less work to create, less work to debug, less work to add a new state because we handle each state separately The design will require more flip-flops than a “minimum flip-flop” implementation May actually reduce combinational logic area • • If flip-flop input equations and circuit output equations are simpler as a result… But this is not guaranteed! This means a one-hot design may or may not require more area/delay/power/energy…

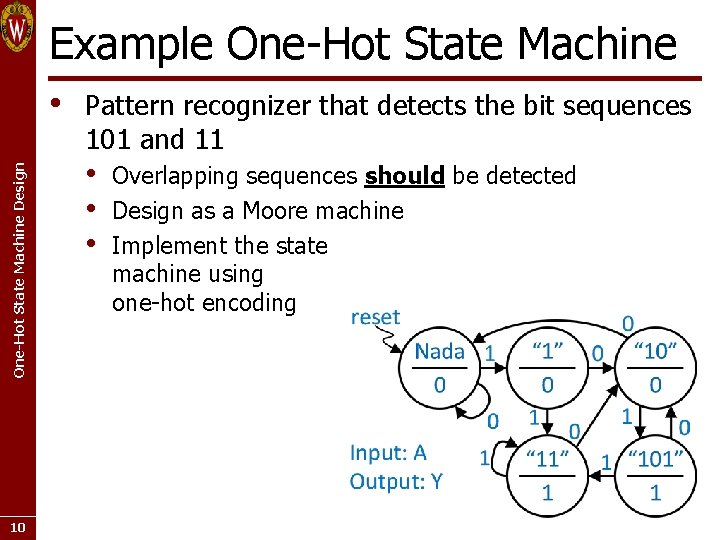
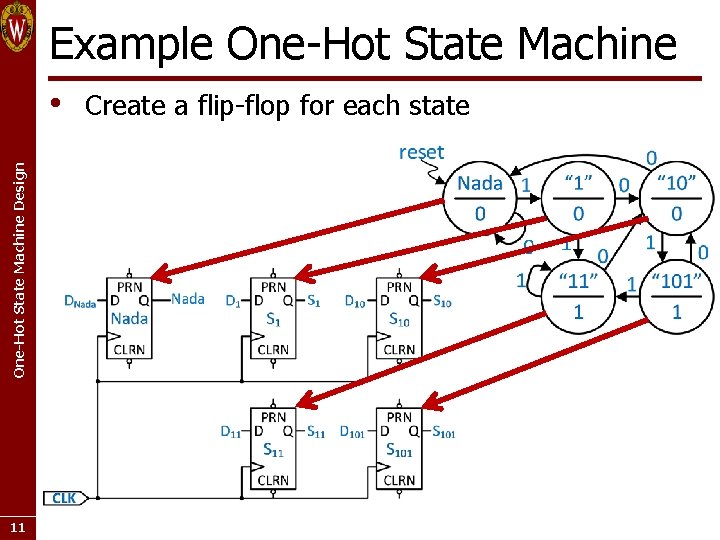
Example One-Hot State Machine Design • 10 Pattern recognizer that detects the bit sequences 101 and 11 • • • Overlapping sequences should be detected Design as a Moore machine Implement the state machine using one-hot encoding

Example One-Hot State Machine Design • 11 Create a flip-flop for each state

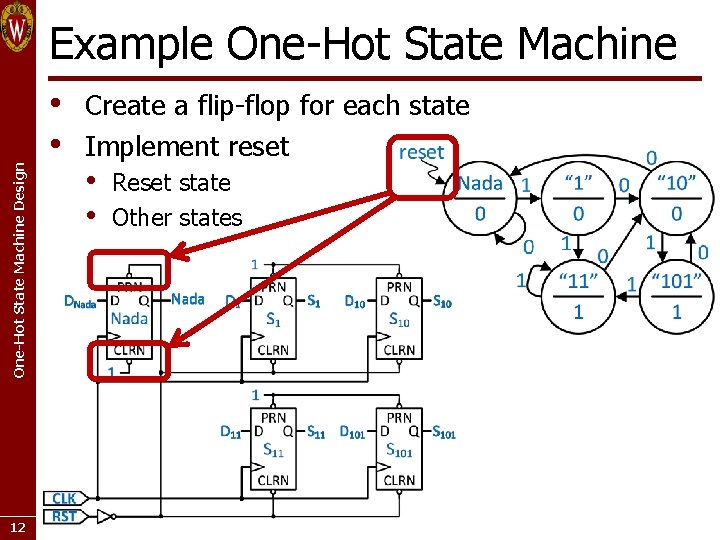
One-Hot State Machine Design Example One-Hot State Machine 12 • • Create a flip-flop for each state Implement reset • • Reset state Other states

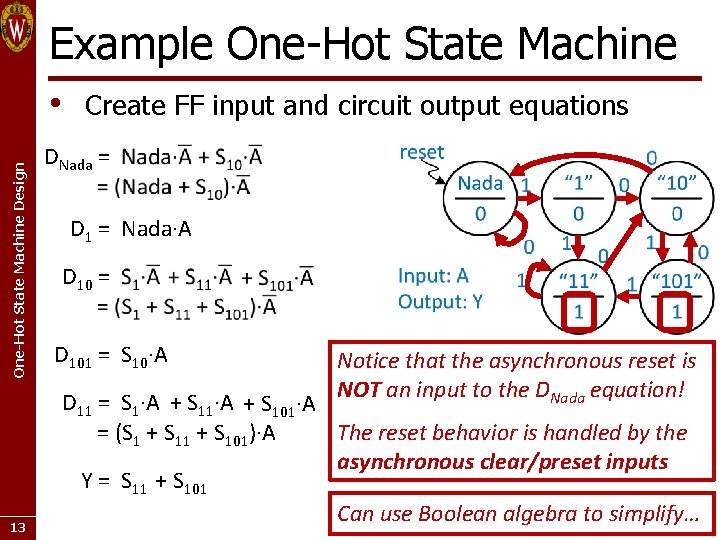
Example One-Hot State Machine Design • 13 Create FF input and circuit output equations DNada = D 1 = Nada·A D 10 = D 101 = S 10·A Notice that the asynchronous reset is NOT an input to the DNada equation! D 11 = S 1·A + S 101·A = (S 1 + S 101)·A The reset behavior is handled by the asynchronous clear/preset inputs Y = S 11 + S 101 Can use Boolean algebra to simplify…

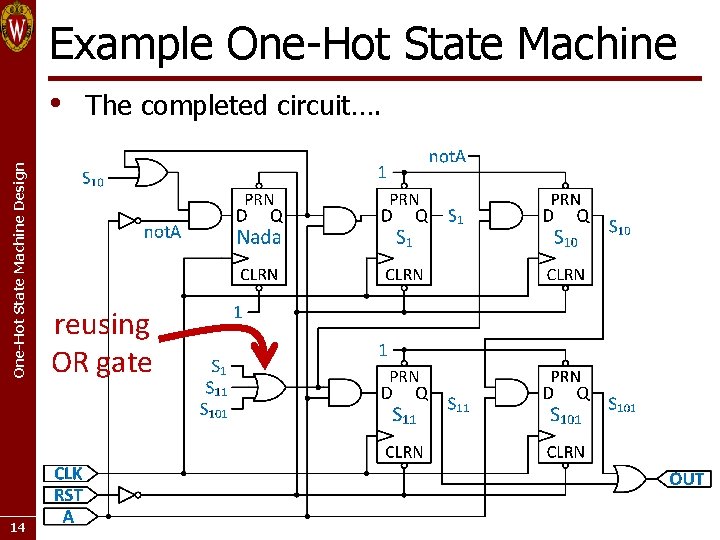
Example One-Hot State Machine Design • 14 The completed circuit…. reusing OR gate

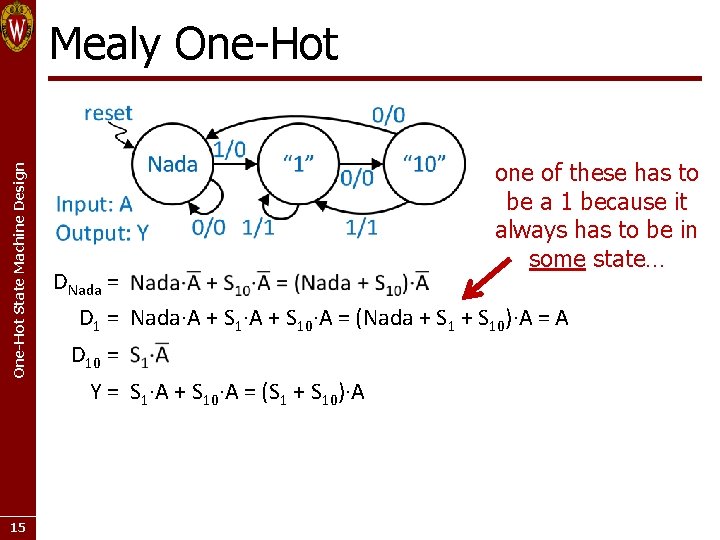
One-Hot State Machine Design Mealy One-Hot 15 one of these has to be a 1 because it always has to be in some state… DNada = D 1 = Nada·A + S 10·A = (Nada + S 10)·A = A D 10 = Y = S 1·A + S 10·A = (S 1 + S 10)·A

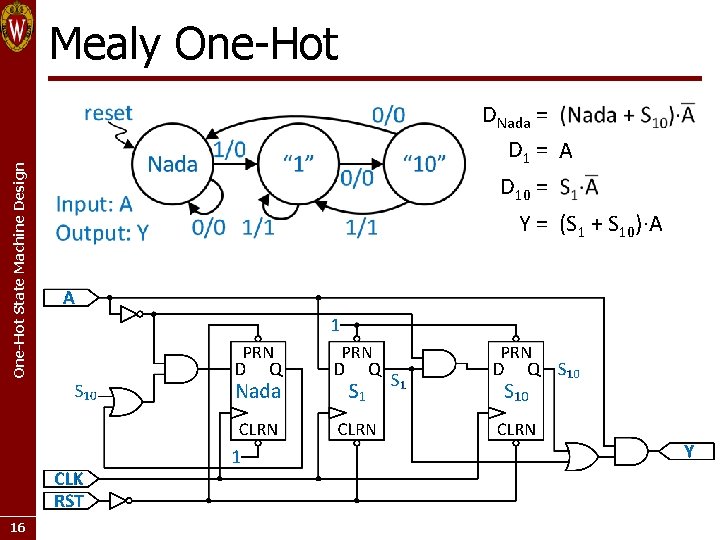
One-Hot State Machine Design Mealy One-Hot 16 DNada = D 1 = A D 10 = Y = (S 1 + S 10)·A

Optimizing One-Hot FSMs One-Hot State Machine Design • • Design simplicity is a major motivating factor! Some simplifications are straightforward, and can save time when drawing the schematic • • • 17 The logic equations from the direct translation may not be as simplified as they could be Optimization may not be critical; we already decided to use more flip-flops than the minimum e. g. , the factorization in the Moore example The downside is that changes may be less straightforward when debugging or modifying the FSM In this class, you do not have to simplify one-hot equations (it will be easier to debug!)

One-Hot State Machine Design 18 ECE 352 Digital System Fundamentals One-Hot State Machine Design