OneDimensional Bound States Bound and Unbound States To

One-Dimensional Bound States Bound and Unbound States To understand the nature of solutions, compare energy to potential at • Classically, there are two types of solutions to these equations – Bound States are when E < V( ). – Unbound states are when E > V( ) • Quantum mechanically, there are bound and unbound states as well, with the same criteria – Bound states are a little easier to understand, so V(x) we’ll do these first E > V( ) E < V( )

Wave Function Constraints The wave function (x) must be continuous Its derivative must exist everywhere Its derivative must be continuous* Its second derivative must exist everywhere* The wave function must be properly normalized† • Must not blow up at *Except where V(x) is infinite †There are exceptions and ways around this problem 1. 2. 3. 4. 5. Normalization What if the wave function is not properly normalized? • If the integral is finite, multiply by a constant to fix it – Modified wave satisfies Schrödinger • If the integral is infinite, it gets complicated – For bound states, this is still trouble – For unbound states, it is okay

The 1 D Infinite Square Well (1) V(x) • Outside of the well, the wave function must vanish • In remaining region, we need to solve differential equation • What functions are minus their second derivative? • We prefer real Boundary Conditions • Must vanish at x = 0 • And at x = L – Where does sin vanish? • Don’t worry about derivative because V(x) blows up there

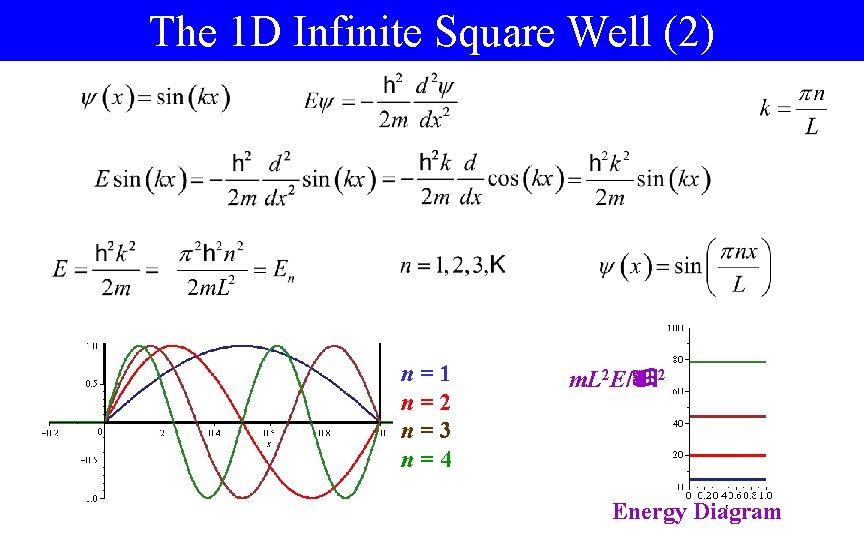
The 1 D Infinite Square Well (2) n=1 n=2 n=3 n=4 m. L 2 E/ 2 Energy Diagram

The 1 D Infinite Square Well (3) BUT WAIT: What about normalization? To fix it: multiply by (2/L). • The most general solution is superposition of this solution

The Finite Square Well (1) I • We need to solve equation in all three regions; this takes work • In region II, we get solutions like before – No longer necessary that it vanish at the boundaries • In regions I and III, we solve a different equation: • If we are looking at bound state (E < V 0), in these regions, we get exponentials II III

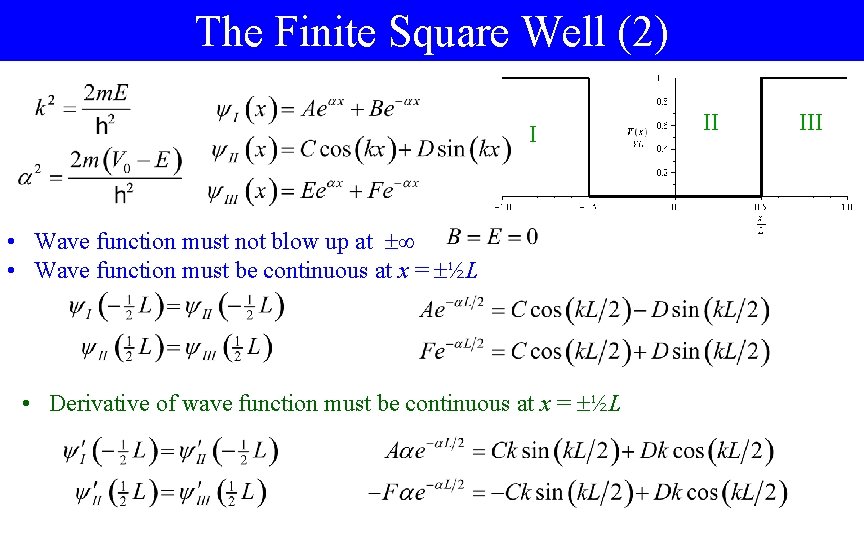
The Finite Square Well (2) I • Wave function must not blow up at • Wave function must be continuous at x = ½L • Derivative of wave function must be continuous at x = ½L II III

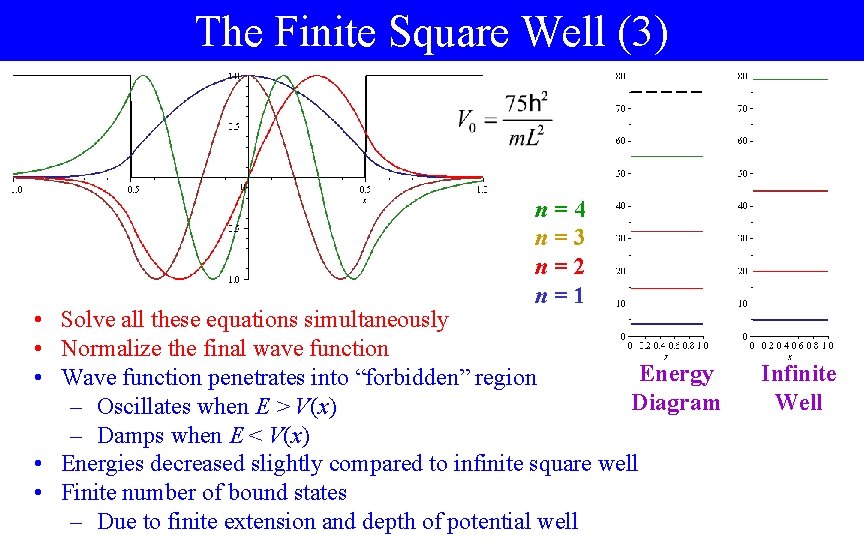
The Finite Square Well (3) n=4 n=3 n=2 n=1 • Solve all these equations simultaneously • Normalize the final wave function Energy • Wave function penetrates into “forbidden” region Diagram – Oscillates when E > V(x) – Damps when E < V(x) • Energies decreased slightly compared to infinite square well • Finite number of bound states – Due to finite extension and depth of potential well Infinite Well

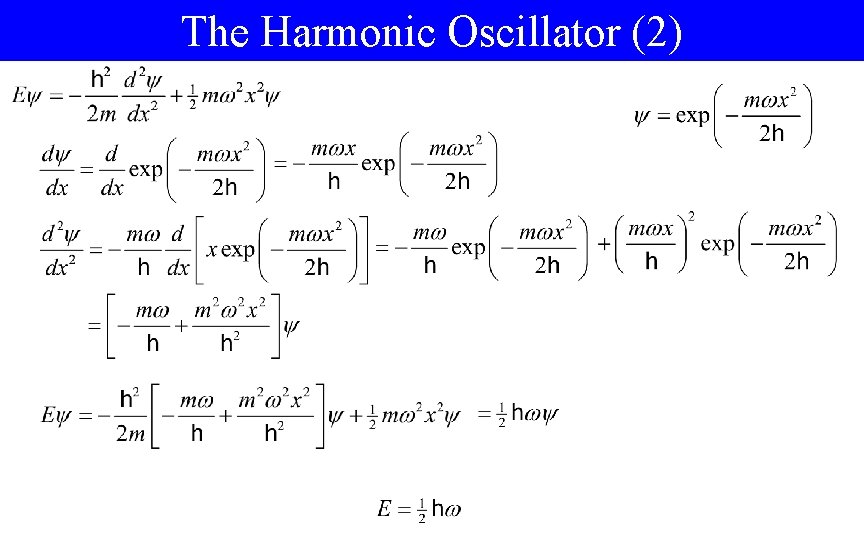
The Harmonic Oscillator (1) • At large x, the behavior is governed (mostly) by the x 2 term • Now we guess • Don’t want it blowing up at infinity! Our strategy: • Check that this works • Find more solutions and check them

The Harmonic Oscillator (2)

The Harmonic Oscillator (3) • We still need to normalize it • Expect other solutions to have similar behavior, at least at large x – We will guess the nature of these solutions • Multiply the wave function above by an arbitrary polynomial P(x) • Substitute in and see if it works – This will give you En n=3 n=2 n=1 n=0