One dimensional models of hydraulic fracture Anthony Peirce

One dimensional models of hydraulic fracture Anthony Peirce (UBC) Collaborators: Jose` Adachi (SLB) Shira Daltrop (UBC) Emmanuel Detournay (UMN) WITS University 1 April 2009

Outline • The HF problem and 2 D models • Slender geometries -> the possibilities for 1 D models • The classic PKN model – porous medium eq – limitations • Extension of PKN to include toughness - 1 D integro-PDE • P 3 D model – PKN methodology ->pseudo 3 D • Conclusions 2

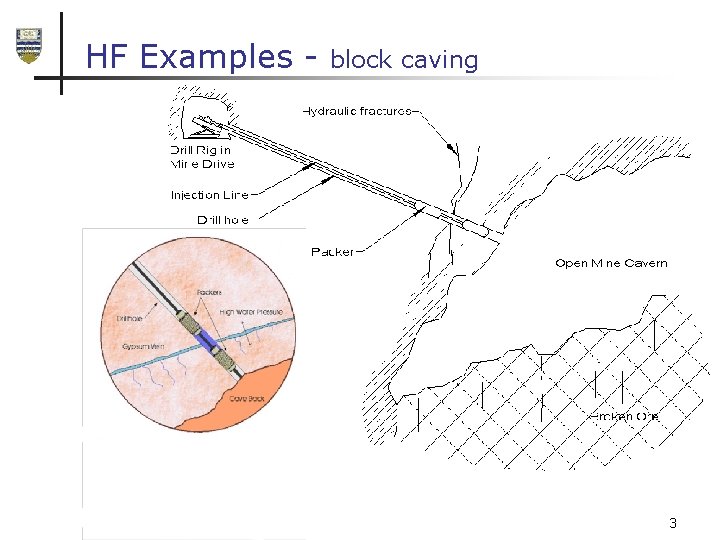
HF Examples - block caving 3

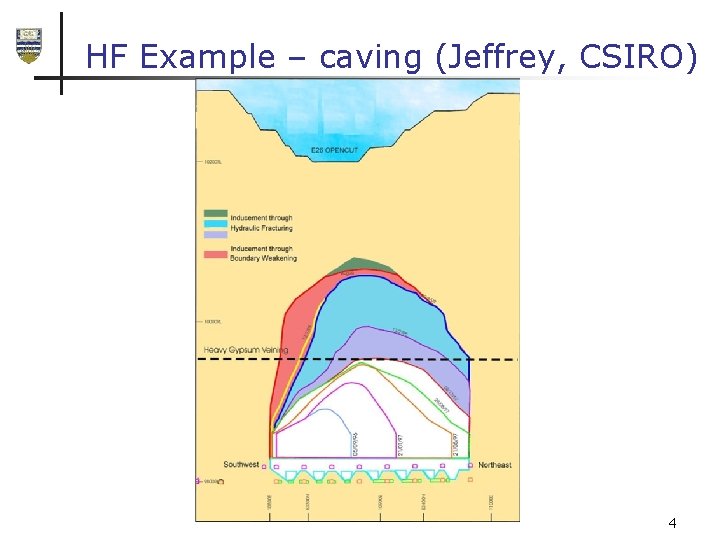
HF Example – caving (Jeffrey, CSIRO) 4

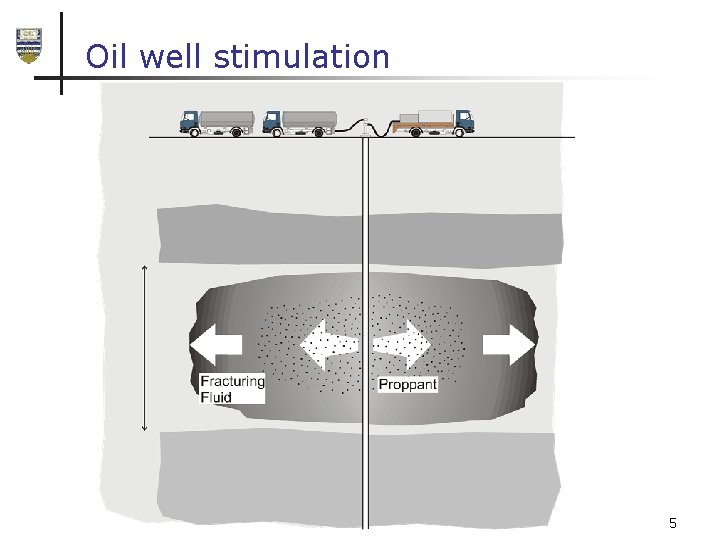
Oil well stimulation 5

Lab test with stress contrast (Bunger) 6

2 -3 D HF Equations • Elasticity (non-locality) • Lubrication (non-linearity) • Boundary conditions at moving front (free boundary) 7

8

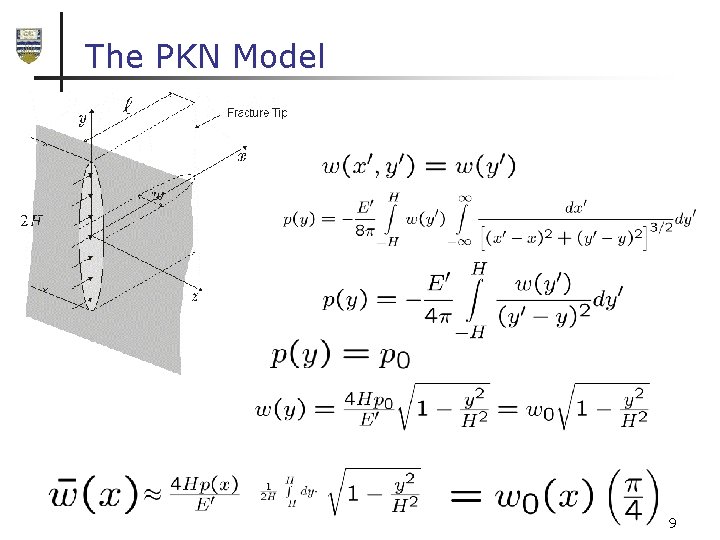
The PKN Model 9

Assumptions behind the PKN Model • Pressure independent of : • Vertical sections approximately in a state of plane strain: • PKN model: Ø Local elasticity equation Ø Can’t model pressure singularities for example when 10

PKN – Averaging the Lubrication Eq 11

Scaled lubrication & similarity solution 12

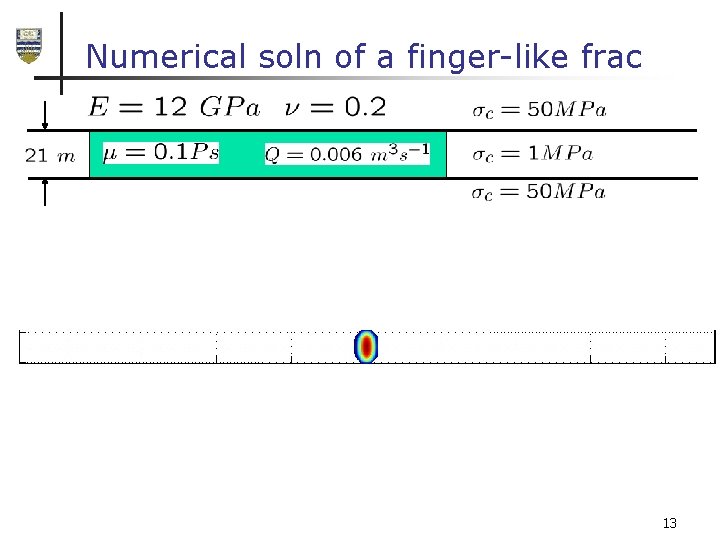
Numerical soln of a finger-like frac 13

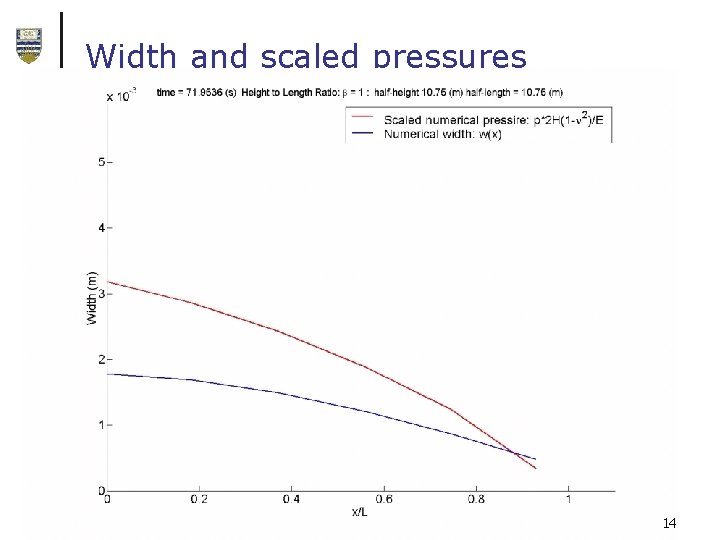
Width and scaled pressures 14

Asymptotics of numerical soln 15

Extended PKN: 2 D integral eq 1 D integral eq • Integral eq for a pressurized rectangular crack • Re-scale variables: 16

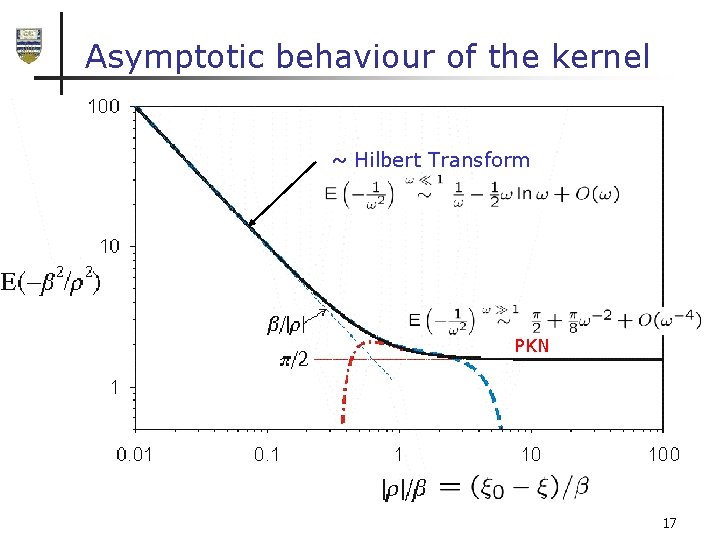
Asymptotic behaviour of the kernel ~ Hilbert Transform PKN 17

Assumed behaviour of § Power law in the tip regions: § Analytic away from the tips: 18

Outer expansion Hilbert Transform Region PKN 19

Outer expansion Test function: 20

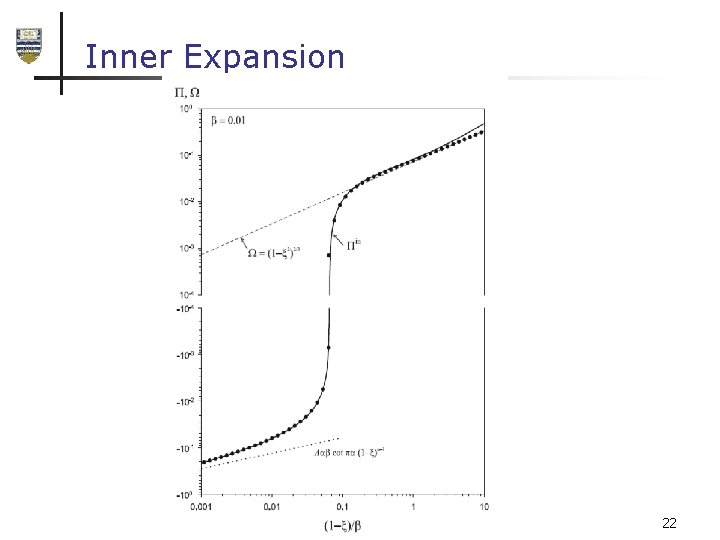
Inner expansion: Hilbert Transform Region PKN Region 21

Inner Expansion 22

Discretizing the Elasticity Equation 23

Discretizing the Fluid Flow Equation 24

EPKN Tip solutions – viscosity Close to the tip 25

Locating the tip position Viscosity Dominated: Toughness Dominated: 26

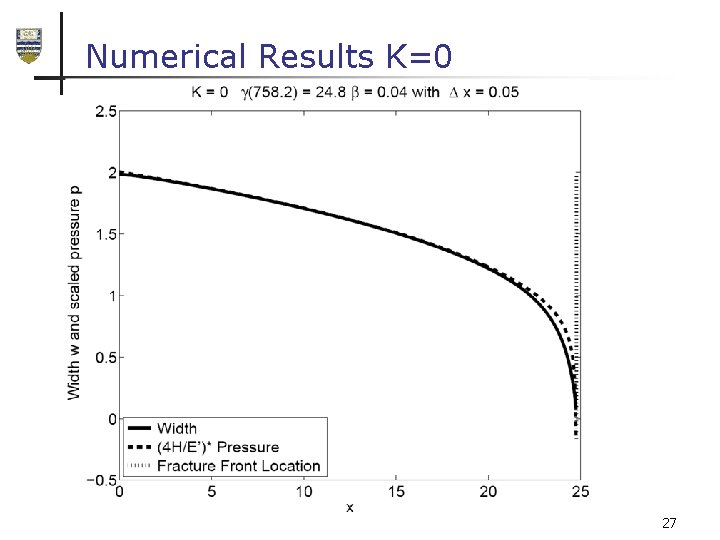
Numerical Results K=0 27

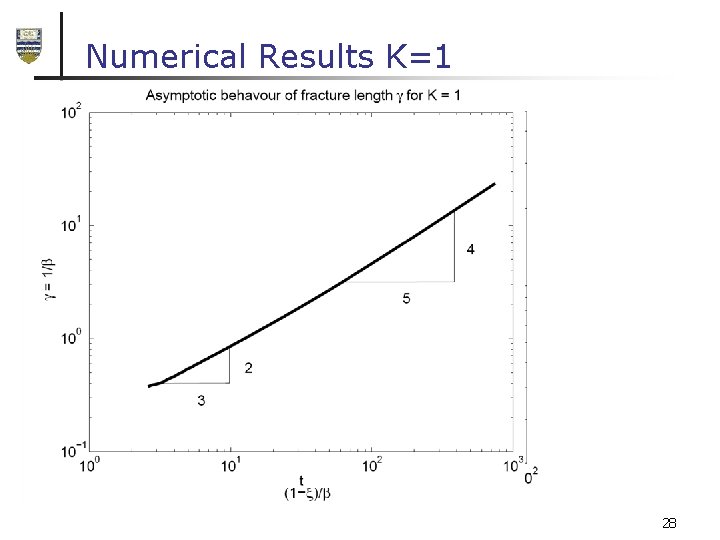
Numerical Results K=1 28

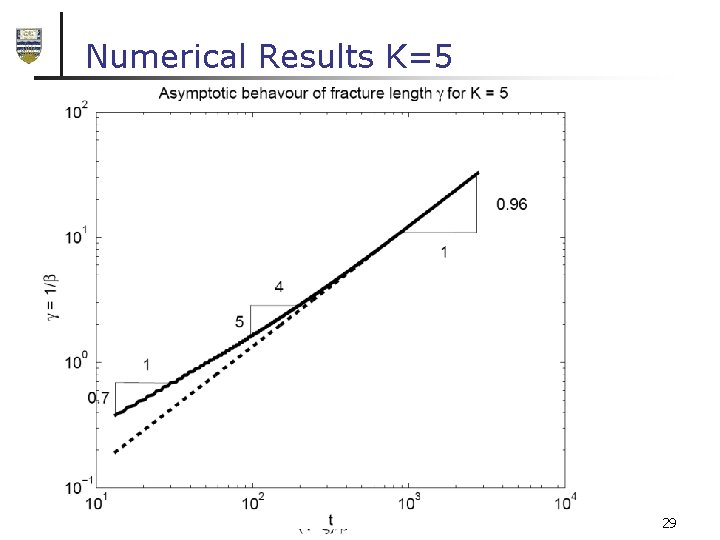
Numerical Results K=5 29

P 3 D models 30

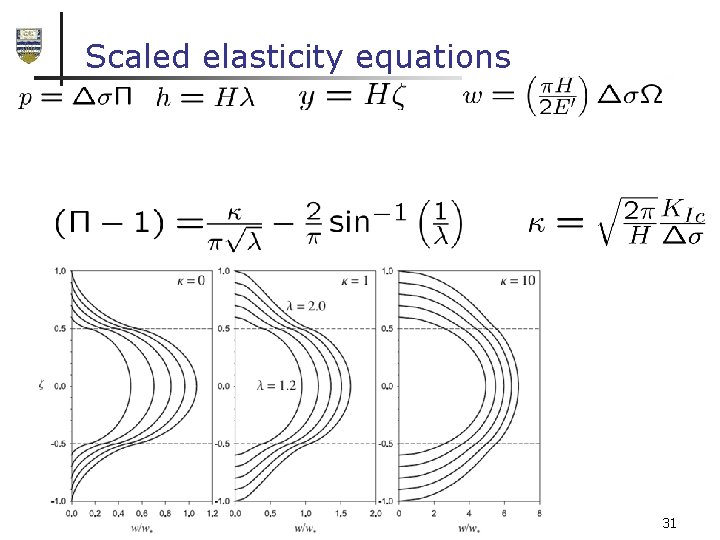
Scaled elasticity equations 31

Averaged equations 32

Scaled lubrication equation 33

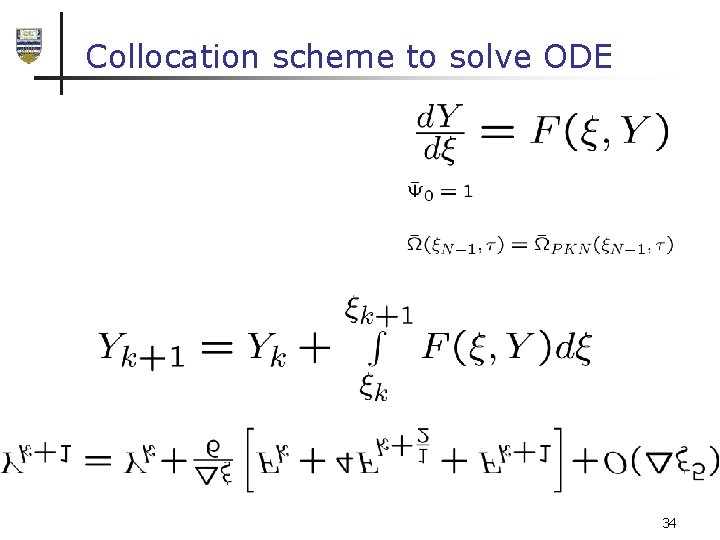
Collocation scheme to solve ODE 34

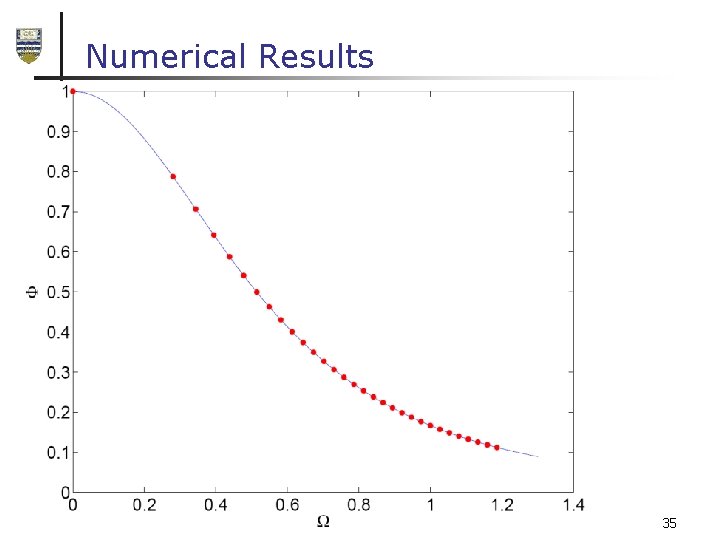
Numerical Results 35

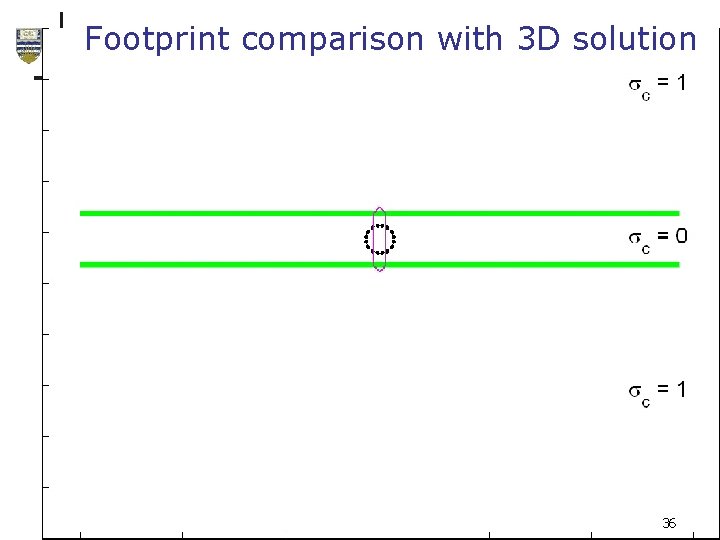
Footprint comparison with 3 D solution 36

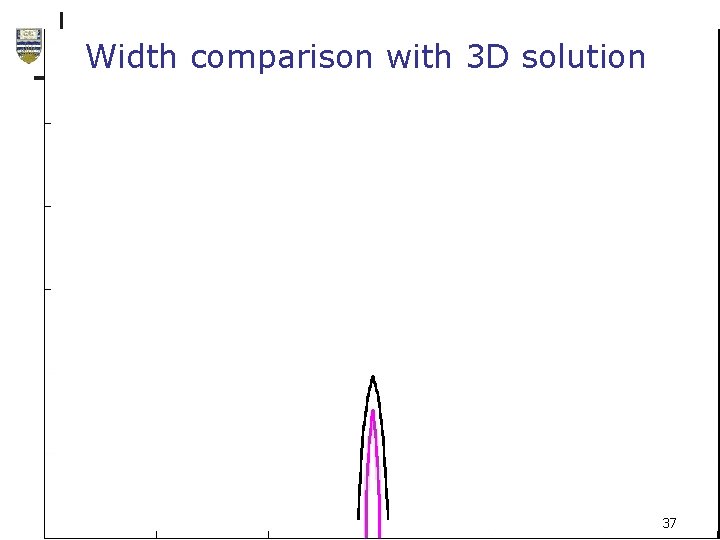
Width comparison with 3 D solution 37

Concluding remarks • • The HF problem and 2 D models Slender geometries -> the possibilities for 1 D models The classic PKN model – porous medium eq - limitations Extension of PKN to include toughness - 1 D integro-PDE Ø Reduction of the 2 D integral to a 1 D nonlocal equation in the small aspect ratio limit Ø Asymptotics of the 1 D kernel Ø Asymptotic analysis to determine the action of the integral operator in different regions of the domain: v Outer region: 1 D integral equation - local PDE v Inner tip region: 1 D integral equation - Hilbert Transform Ø Tip asymptotics and numerical solution • P 3 D model – PKN methodology ->pseudo 3 D Ø Ø Ø Plane strain width solution and averaging Averaging and scaling the lubrication Reduction to a convection diffusion equation Numerical solution via collocation Results and comparison with 3 D solution 38

PKN Traveling Wave solution 39