Once upon a time Eulers problem 1936 Knigsbergs

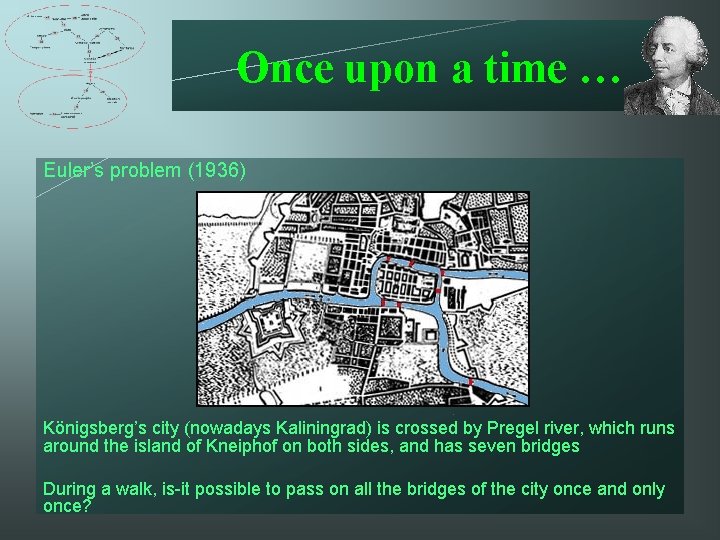
Once upon a time … Euler’s problem (1936) Königsberg’s city (nowadays Kaliningrad) is crossed by Pregel river, which runs around the island of Kneiphof on both sides, and has seven bridges During a walk, is-it possible to pass on all the bridges of the city once and only once?

Some references … • König, D. (1936). Theorie der endlichen und unendlichen Graphen. König, D. (1990). Theory of finite and infinite graphs. Berlin: Birkhauser • Berge, C. (1958). Théorie des graphes et ses applications. Paris: Dunod. English edition, Wiley 1961; Methuen & Co, New York 1962; Dover, New York 2001. Russian, Moscow 1961; Spanish, Mexico 1962; Roumanian, Bucharest 1969; Chinese, Shanghai 1963;

Some references … 3 fundamental articles to use similitude analysis in the social representations’ domain Flament (1962). L’analyse de similitude. Cahiers du Centre de Recherche Opérationnelle, 4, 63 -97 Degenne, A. & Vergès, P. (1973). Introduction à l’analyse de similitude. Revue française de Sociologie, 14, 471 -512 Flament, C. , Degenne, A. & Vergès, P. (1971). Similarity Analysis. Paris: Maison des Sciences de l’Homme.

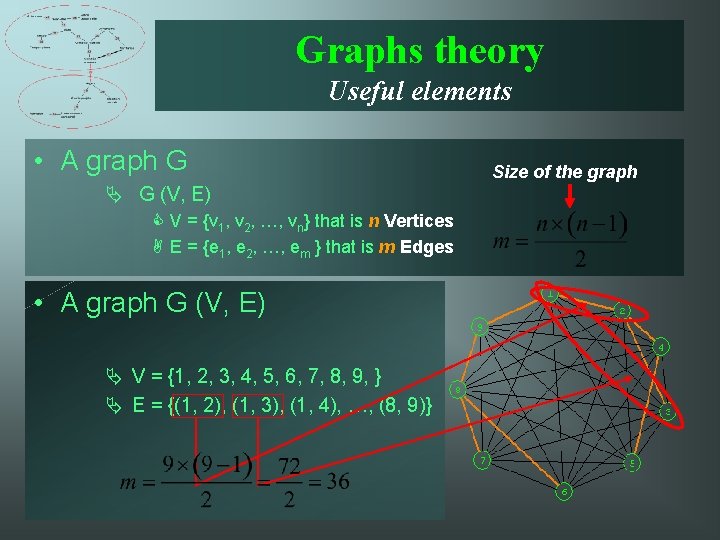
Graphs theory Useful elements • A graph G Ä G (V, E) C V = {v 1, v 2, …, vn} that is n Vertices A E = {e 1, e 2, …, em } that is m Edges • A graph G (V, E) Ä V = {1, 2, 3, 4, 5, 6, 7, 8, 9, } Ä E = {(1, 2), (1, 3), (1, 4), …, (8, 9)} Size of the graph

Graphs theory Useful elements G(V, E) – – V = {1, 2, 3, 4, 5} E = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)} G(V, E) – – V’ = {1, 2, 3} E’ = {(1, 2), (1, 3), (2, 3)} Some vertices = subgraph of G G(V, E) – V’ = {1, 2, 3, 4, 5} – E’ = {(1, 2), (3, 4), (4, 5)} All the vertices, some edges = Spanning Subgraph of G

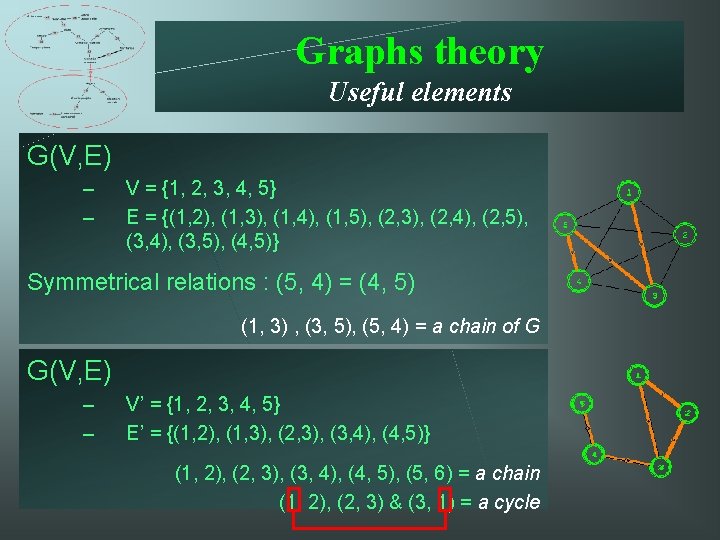
Graphs theory Useful elements G(V, E) – – V = {1, 2, 3, 4, 5} E = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)} Symmetrical relations : (5, 4) = (4, 5) (1, 3) , (3, 5), (5, 4) = a chain of G G(V, E) – – V’ = {1, 2, 3, 4, 5} E’ = {(1, 2), (1, 3), (2, 3), (3, 4), (4, 5)} (1, 2), (2, 3), (3, 4), (4, 5), (5, 6) = a chain (1, 2), (2, 3) & (3, 1) = a cycle

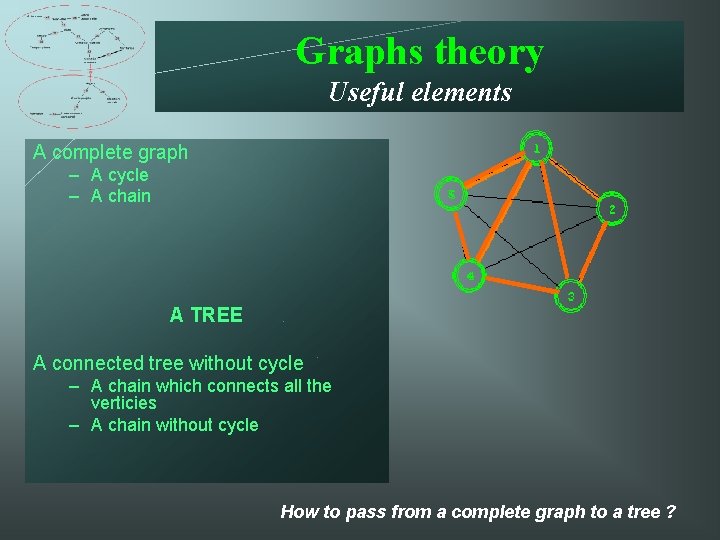
Graphs theory Useful elements A complete graph – A cycle – A chain A TREE A connected tree without cycle – A chain which connects all the verticies – A chain without cycle How to pass from a complete graph to a tree ?

Useful elements for SR How to pass from a complete graph to a tree ? Searching for the structure of the relations = Searching for the skeleton of the representation = Searching for a tree Each edge has a weight = Similitude analysis ￫ weight = similitude index = Co-occurrence, symmetrical co-occurrence, Phi square measure, Correlation, squared index of similitude (Guimelli), etc.

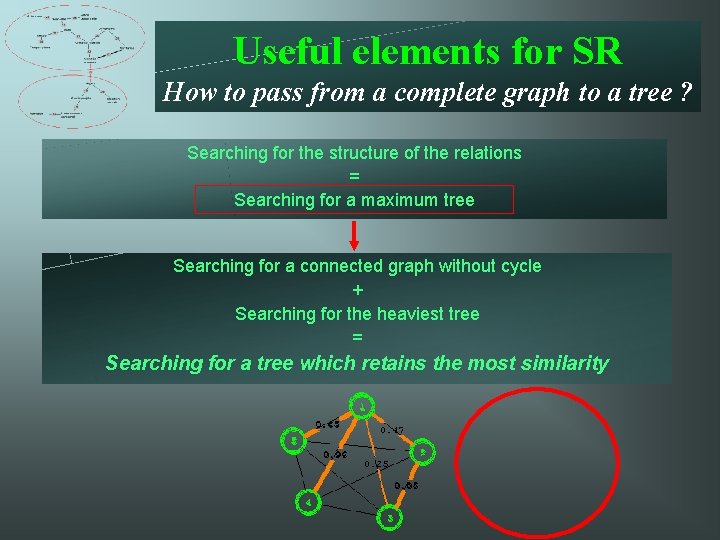
Useful elements for SR How to pass from a complete graph to a tree ? Searching for the structure of the relations = Searching for a maximum tree Searching for a connected graph without cycle + Searching for the heaviest tree = Searching for a tree which retains the most similarity

Let us return to our example …

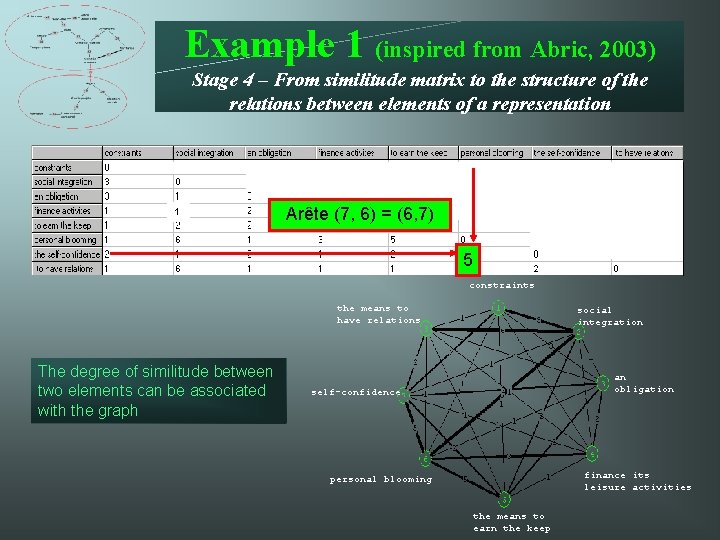
Example 1 (inspired from Abric, 2003) Stage 4 – From similitude matrix to the structure of the relations between elements of a representation 1 Arête (7, 6) = (6, 7) 5 constraints the means to have relations The degree of similitude between two elements can be associated with the graph social integration an obligation self-confidence finance its leisure activities personal blooming the means to earn the keep

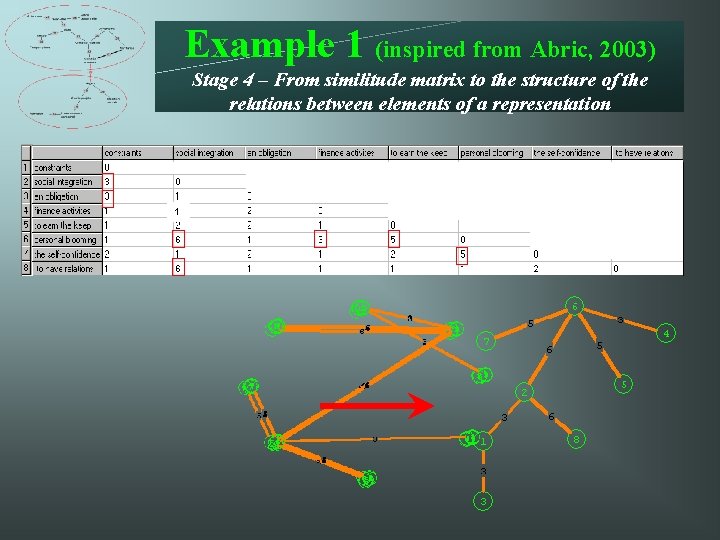
Example 1 (inspired from Abric, 2003) Stage 4 – From similitude matrix to the structure of the relations between elements of a representation 1

Example 1 (inspired from Abric, 2003) Stage 4 – From similitude matrix to the structure of the relations between elements of a representation 1 Edges S 1 (2, 6) 6 (1, 7) 2 (1, 4) 1 (3, 6) 1 (2, 8) 6 (2, 5) 2 (1, 5) 1 (3, 8) 1 (5, 6) 5 (3, 4) 2 (1, 6) 1 (4, 5) 1 (6, 7) 5 (3, 5) 2 (1, 8) 1 (4, 7) 1 (1, 2) 3 (3, 7) 2 (2, 3) 1 (4, 8) 1 (1, 3) 3 (5, 7) 2 (2, 4) 1 (5, 8) 1 (4, 6) 3 (7, 8) 2 (2, 7) 1 (6, 8) 1

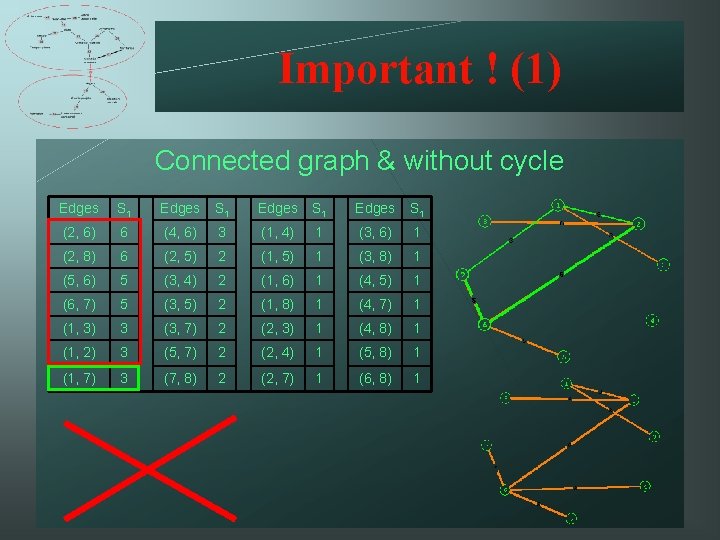
Important ! (1) Connected graph & without cycle Edges S 1 (2, 6) 6 (4, 6) 3 (1, 4) 1 (3, 6) 1 (2, 8) 6 (2, 5) 2 (1, 5) 1 (3, 8) 1 (5, 6) 5 (3, 4) 2 (1, 6) 1 (4, 5) 1 (6, 7) 5 (3, 5) 2 (1, 8) 1 (4, 7) 1 (1, 3) 3 (3, 7) 2 (2, 3) 1 (4, 8) 1 (1, 2) 3 (5, 7) 2 (2, 4) 1 (5, 8) 1 (1, 7) 3 (7, 8) 2 (2, 7) 1 (6, 8) 1

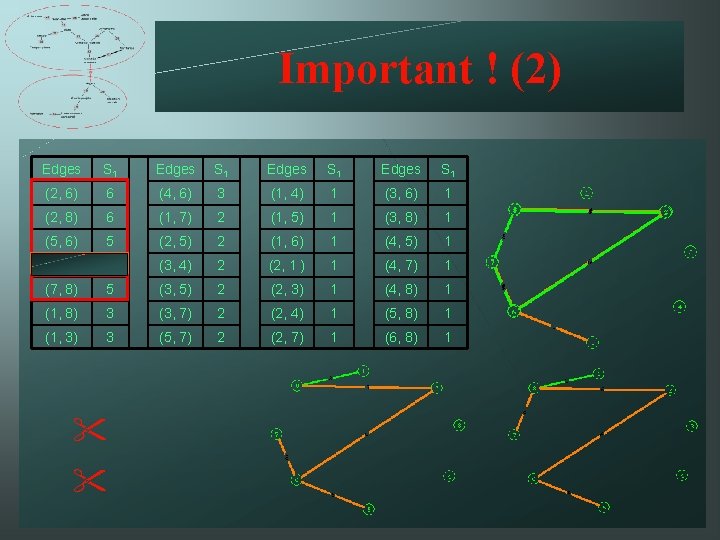
Important ! (2) Edges S 1 (2, 6) 6 (4, 6) 3 (1, 4) 1 (3, 6) 1 (2, 8) 6 (1, 7) 2 (1, 5) 1 (3, 8) 1 (5, 6) 5 (2, 5) 2 (1, 6) 1 (4, 5) 1 (6, 7) 5 (3, 4) 2 (2, 1 ) 1 (4, 7) 1 (7, 8) 5 (3, 5) 2 (2, 3) 1 (4, 8) 1 (1, 8) 3 (3, 7) 2 (2, 4) 1 (5, 8) 1 (1, 3) 3 (5, 7) 2 (2, 7) 1 (6, 8) 1

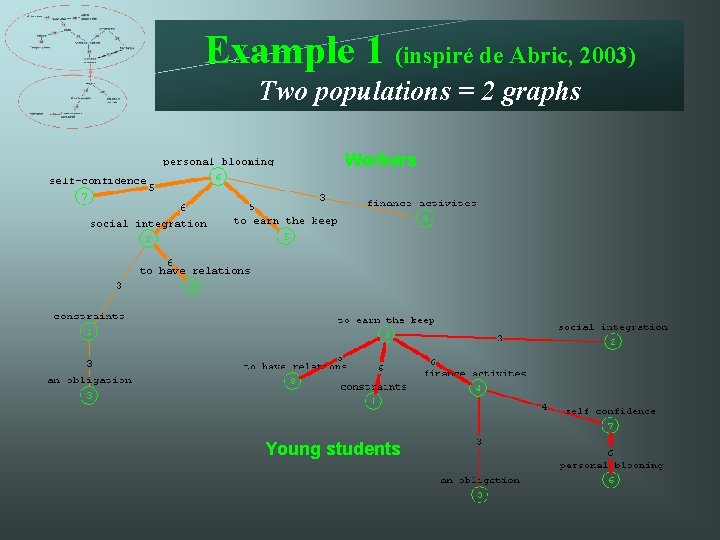
Example 1 (inspiré de Abric, 2003) Two populations = 2 graphs Workers Young students