On using a functional measure to capture the

On using a functional measure to capture the probabilistic character of measurement in quantum mechanics Erik Deumens UFIT Research Computing & Quantum Theory Project Dept. of Physics and Dept. of Chemistry University of Florida 9/8/2019 1

Some history • 1926 – Birth of quantum mechanics • The correct mathematical formulation! • Never contradicted by any finding since! • Heisenberg, Jordan, Born, Schrödinger, Dirac, … • 1900 – 1926 – today – Discussion about quantum mechanics • Arguments about quantum phenomena… • Invention of contradicting interpretations… • Planck, Einstein, Bohr, … 9/8/2019 2

Scientific method Phenomenology - Description Theory - Explanation • 1619 – Kepler – laws of planetary motion • 1869 – Mendeleev – Periodic table of elements • 1926 – Born – Probability rule • 1687 – Newton – Law of force and law of gravity • 1913 – Bohr – Atomic theory of elements and chemical bonding • 2013 – Allaverdyan, Balian, Nieuwenhuizen – derivation of Born’s rule from Liouville-von Neumann equation 9/8/2019 3

Some philosophy

The mystery of quantum mechanics 9/8/2019 5

Tomomura, Endo, Matsuda, Kawasaki, Exawa Amer. J. Phys, 57, p. 117 (1989) 9/8/2019 6

The math of mechanics

The measurement of systems Classical – direct measurement Quantum – Born probability rule • System state values q • Detector state values r • Measurement process is simple dynamics • Can be approximated by simple transfer of values q -> r • Probability is incidental and comes from inaccuracies and uncertainties • System state function ψ • Detector state values r • Measurement process is complex • Born rule P(q)=|ψ(q)|2 gives probability for q -> r • Probability is intrinsic 9/8/2019 8

A circular argument 9/8/2019 9

How does this work? • Quantum dynamics evolves wave functions ψ(q) • Interaction with measurement apparatus produces a value q • Value q is recorded from apparatus • clearly q is a property of the apparatus • Einstein-Bohr assumption • q is also a property of the system • How does q line up with the wave function ψ(q) ? • Unending controversy… 9/8/2019 10

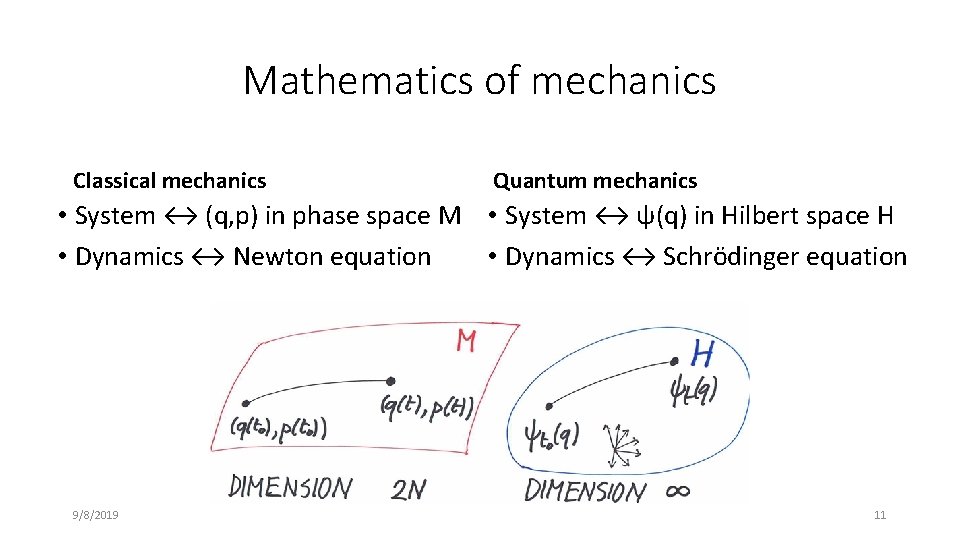
Mathematics of mechanics Classical mechanics Quantum mechanics • System ↔ (q, p) in phase space M • System ↔ ψ(q) in Hilbert space H • Dynamics ↔ Newton equation • Dynamics ↔ Schrödinger equation 9/8/2019 11

Superposition and entanglement 9/8/2019 12

Schmidt decomposition and density matrix

von Neumann density matrix • Gemenge – ensemble of systems • With statistical probability of being in one of several wave functions • Wave functions -> D • Reconstruction not unique: D -> wave functions 9/8/2019 14

Measure theory (mathematics) • Lebesgue measure • translation invariant • universal reference • Probability measures • Finite measure μ(M)=1 • Density matrix • Measure on subspaces of Hilbert space • Measures on ∞-dim spaces • No Lebesgue exists • Finite measures exist 9/8/2019 15

Probability in quantum mechanics Statistical interpretation Functional measure view • Wave functions – Schrödinger equation • Density matrix – Liouville-von. Neumann equation • Probabilistic nature of wave function cannot be separated from that of density matrix • Same • No probability interpretation • Deny Born rule • Functional probability measure • Flow induced by SE • Probabilistic nature of QM lies in the measure • Same as in classical stat. mech. 9/8/2019 16

Mathematics of probability and statistics Classical statistics Quantum statistics • Probability density ρ(q, p) • Probability measure μ on M • Can have functional measure, • But no density w. r. t. Lebesgue • Probability measure μ on H 9/8/2019 17

Statistical state in quantum mechanics 9/8/2019 18

Gaussian measures 19 9/8/2019

Observable A, self-adjoint opera 20 9/8/2019

Measurement theory (physics) • Wave functions are theoretical foundation • Not directly accessible to experiment • System being observed is in a narrow statistical state • Carefully prepared • All system wave functions with weight are very similar, experimentally indistinguishable • Detector is always in a broad statistical state • Impossible to prepare precisely – has Avogadro number of degrees of freedom 1023 • Many detector wave functions with weight are very different, with different macroscopic outcomes for the measurement process 9/8/2019 21

Detector statistics and dynamics • Electron statistical state – sharp – one wave function • Detector statistical state – broad – very many wave functions – many superpositions • Electron interacts with all mini detectors – all in different wave functions – some: fly through – some: excite few molecules, not enough to see – one: excites 500 molecules and sends 500 photons • Photons are captured – fly through optical fiber – excite secondary electrons – current detected – write bit in RAM – display dot on screen 9/8/2019 22

Emergence of classical systems • One mini detector has 500 molecules with 30 atoms – 15, 000 degrees of freedom • Variance of the collective variable that tracks excitation of mini detector is square root of N=15, 000, which is 122 – two orders less than one molecule • That makes the collective variable effectively dispersionless = classical • We define this to be a q-classical variable • A set of q-classical variables can form a q-classical system • By Ehrenfest theorem, q-classical evolution follows Newton equation 9/8/2019 23

Where do probabilities come from? • From the statistical state of the quantum system! • It gives many random wave functions for every macroscopic system – for all mini detectors in an experimental apparatus • The mini-detector collective variable tracking excitation of 500 photons follows classical dynamics • The mini-detector that gets excited is the random selection of the statistical state evolution • The measurement then proceeds classically – the result is recorded 9/8/2019 24

From deterministic to probabilistic • Wave functions are fundamental – functions • Deterministic dynamics by Schrödinger equation • Probability distribution on Hilbert space of wave functions • Evolution of quantum statistical state • Derive q-classical variables and systems – values • Deterministic dynamics by Newton equation follows from Ehrenfest theorem → Recover classical mechanics • Probability distribution on q-classical phase space • Liouville equation for evolution of q-classical statistical state → Recover classical statistical mechanics → Describe probabilistic quantum measurement process 9/8/2019 25

An analogy: photographs and movies Classical mechanics: values Quantum mechanics: functions ANALOGY • 1 photograph ANALOGY • 2 hour movie • 24 frames per second • 172, 800 = 24 x 7, 200 frames • smoothly aligned sequence MATHEMATICS Schrödinger equation • 1 frame • static MATHEMATICS Newton equation 4/4/2019 26

Questions and discussion Slides and paper at https: //people. clas. ufl. edu/deumens 9/8/2019 27

Wave function collapse in space • Position is an operator • Time is a parameter/coordinate • That is inconsistent • Attempts to make time an operator have been made • Make position a coordinate of events • Same as time • Does work well • Even in non-relativistic quantum mechanics 9/8/2019 28