On to Open GL Introduction to Computer Graphics

On to Open. GL Introduction to Computer Graphics and Animation (Principle of Computer Graphics) Rattapoom Waranusast

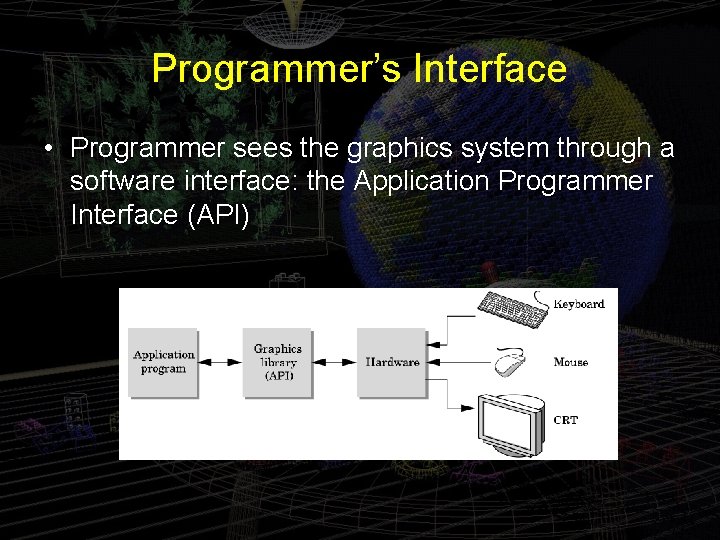
Programmer’s Interface • Programmer sees the graphics system through a software interface: the Application Programmer Interface (API)

SGI and GL • Silicon Graphics (SGI) revolutionized the graphics workstation by implementing the pipeline in hardware (1982) • To use the system, application programmers used a library called GL • With GL, it was relatively simple to program three dimensional interactive applications

Open. GL • The success of GL lead to Open. GL in 1992, a platformindependent API that was – – – Wide availability and hardware support. Easy to use Close enough to the hardware to get excellent performance Device and language independence (portability) Multiple programming language support Stability • Backward compatibility is mandated by the ARB. – Scalability. • It can be implemented in PCs, workstations, supercomputers, consumer electronics (games), and, recently, even mobile phones. – Powerful 3 D graphics.

Open. GL History • Controlled by an Architectural Review Board (ARB) until 2006 (now Khronos Group) – Members include SGI, Microsoft (left in 2003), Nvidia, AMD/ATI, Adobe, Apple, Intel, Google, IBM, Sony, Samsung, Nokia, Sun/Oracle, Mozilla, EA … – Relatively stable (present version 4. 1) • Evolution reflects new hardware capabilities – Allows for platform specific features through extensions • See http: //www. opengl. org for up-to-date info

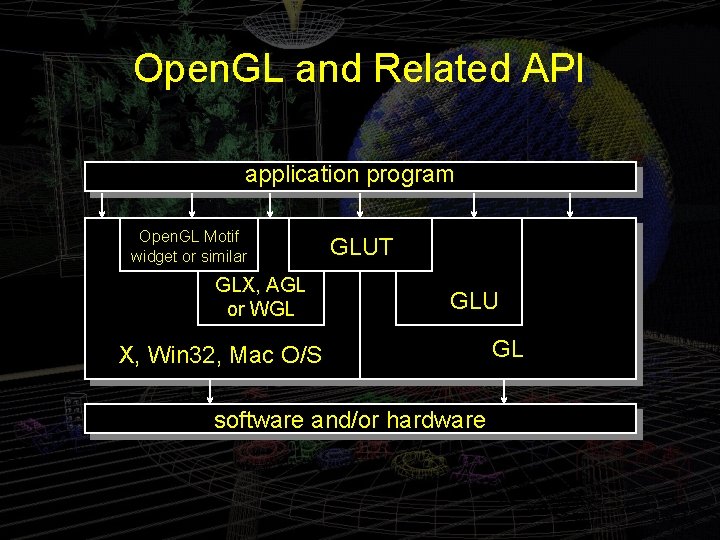
Open. GL Libraries • Open. GL core library (GL, Open. GL 32) – Lowest level: vertex, matrix manipulation • gl. Vertex 3 f(point. x, point. y, point. z) • Open. GL Utility Library (GLU) – Provides functionality in Open. GL core but avoids having to rewrite code – Helper functions for shapes, transformations • glu. Perspective( fovy, aspect, near, far ) • Open. GL Utility Toolkit (GLUT) – Highest level: Window and interface management – Portable windowing API – Not officially part of Open. GL • glut. Swap. Buffers() • Links with window system – GLX for X window systems – WGL for Windows – AGL for Macintosh

Open. GL and Related API application program Open. GL Motif widget or similar GLX, AGL or WGL GLUT GLU X, Win 32, Mac O/S software and/or hardware GL

Windowing with Open. GL • Open. GL is independent of any specific window systems • Open. GL can be used with different window systems – X windows (GLX) – MFC –… • GLUT provide a portable API for creating window and interacting with I/O devices

Open. GL State • Open. GL is a state machine • Open. GL functions are of two types – Primitive generating • Can cause output if primitive is visible • How vertices are processed and appearance of primitive are controlled by the state – State changing • Transformation functions • Attribute functions

Open. GL Conventions • Functions in Open. GL start with gl – Most functions just gl (e. g. , gl. Color()) – Functions starting with glu are utility functions (e. g. , glu. Look. At()) • Note that GLU functions can always be composed entirely from core GL functions – Functions starting with glut are from the GLUT library, built on top of Open. GL and WGL (Windows) or X (Linux) for window management, mouse and keyboard events, etc. • Created and distributed as an entirely different library

Open. GL Conventions • Function names indicate argument type and number – – – Functions ending with f take floats Functions ending with i take ints Functions ending with b take bytes Functions ending with ub take unsigned bytes Functions that end with v take an array. • Examples – gl. Color 3 f() takes 3 floats – gl. Color 4 fv() takes an array of 4 floats

Open. GL #defines • Most constants are defined in the include files gl. h, glu. h and glut. h – Note #include <glut. h> should automatically include the others – Examples – gl. Begin(GL_POLYGON) – gl. Clear(GL_COLOR_BUFFER_BIT) • include files also define Open. GL data types: Glfloat, Gldouble, …

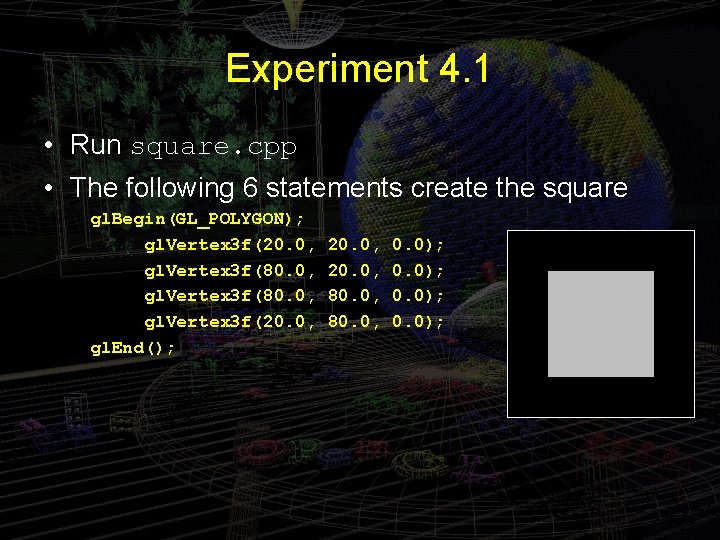
Experiment 4. 1 • Run square. cpp • The following 6 statements create the square gl. Begin(GL_POLYGON); gl. Vertex 3 f(20. 0, gl. Vertex 3 f(80. 0, gl. Vertex 3 f(20. 0, gl. End(); 20. 0, 80. 0, 0. 0);

Experiment 4. 1 • Determine which way the x- and y-axes are oriented. • One way to do that is by changing the vertex coordinates. • The last co-ordinate is obviously the z coordinate.

Open. GL Co-ordinate system y (80, 0) (20, 0) (0, 0) x

Experiment 4. 2 • What exactly do the vertex coordinate value mean? mm. ? cm. ? pixels? • Change the glut. Init. Window. Size() parameter values of square. cpp first to glut. Init. Window. Size(300, 300) and then to glut. Init. Window. Size(500, 250).

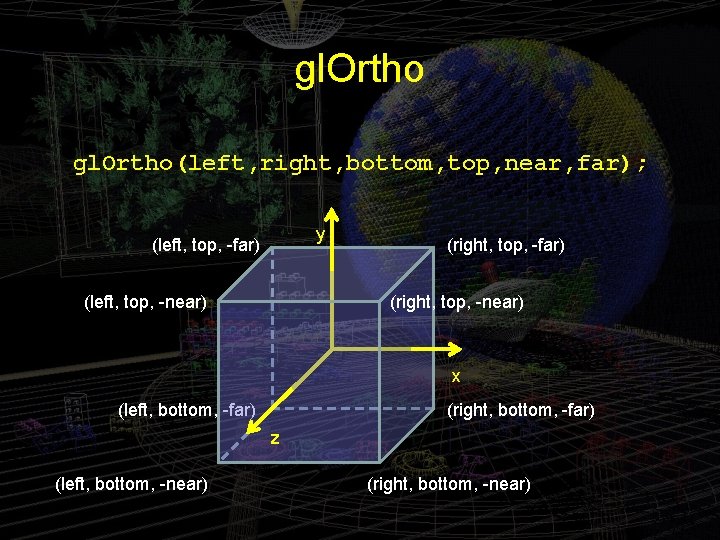
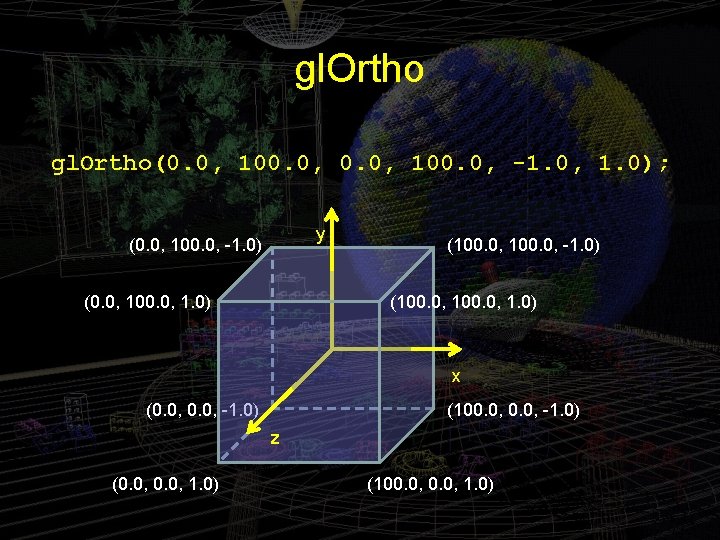
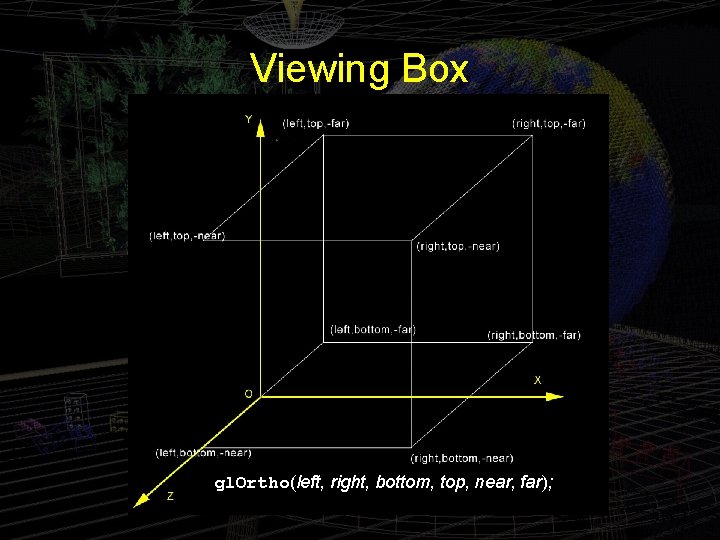
Projection Statement gl. Ortho(0. 0, 100. 0, -1. 0, 1. 0); • In the resize() function, which determine an imaginary view box inside which the programmer draws. • Generally gl. Ortho(left, right, bottom, top, near, far); sets up a viewing box with corners at 8 points.

gl. Ortho(left, right, bottom, top, near, far); y (left, top, -far) (left, top, -near) (right, top, -far) (right, top, -near) x (left, bottom, -far) (right, bottom, -far) z (left, bottom, -near) (right, bottom, -near)

gl. Ortho(0. 0, 100. 0, -1. 0, 1. 0); y (0. 0, 100. 0, -1. 0) (0. 0, 100. 0, 1. 0) (100. 0, -1. 0) (100. 0, 1. 0) x (0. 0, -1. 0) (100. 0, -1. 0) z (0. 0, 1. 0) (100. 0, 1. 0)

Viewing Box gl. Ortho(left, right, bottom, top, near, far);

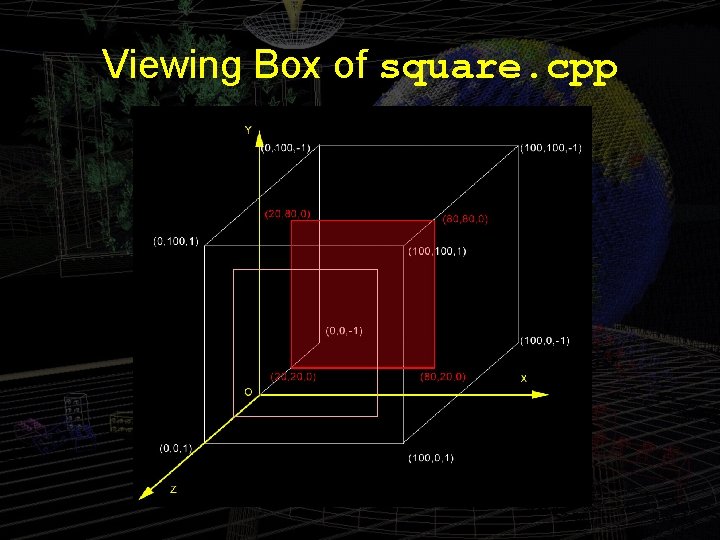
Viewing Box of square. cpp

Rendering Process of gl. Ortho • Shoot – Objects are projected perpendicularly onto the front face of the viewing box. – The front face of the viewing box is called the viewing face and the plane on which is lies the viewing plane. • Print – The viewing face is proportionately scaled to fit the rectangular Open. GL window.

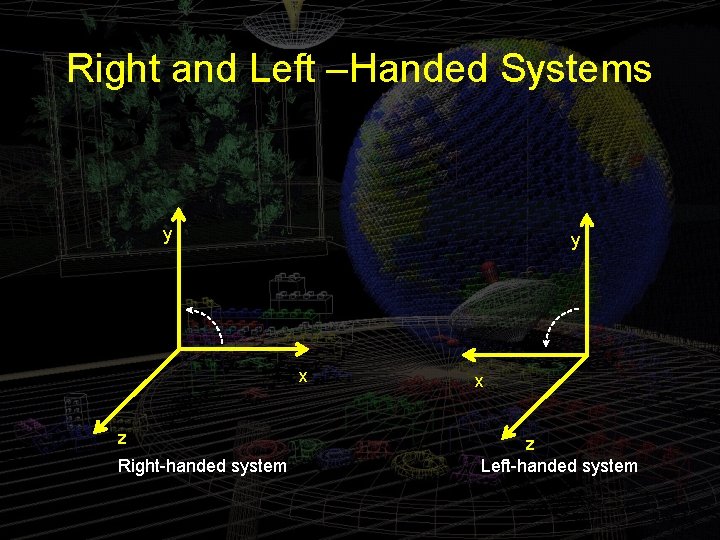
Right and Left –Handed Systems y y x z Right-handed system x z Left-handed system

Experiment 4. 3 • Change only the viewing box of square. cpp by replacing – gl. Ortho(0. 0, 100. 0, -1. 0, 1. 0) with – gl. Ortho(-100. 0, -1. 0, 1. 0). • The location of the square in the new viewing box is different and, so as well, the result of shoot-and-print.

Experiment 4. 3 • Change the viewing box of square. cpp by replacing – gl. Ortho(0. 0, 100. 0, -1. 0, 1. 0) successively with the following, in each case trying to predict the output before running: – gl. Ortho(0. 0, 200. 0, -1. 0, 1. 0) – gl. Ortho(20. 0, 80. 0, -1. 0, 1. 0) – gl. Ortho(0. 0, 100. 0, -2. 0, 5. 0)

Experiment 4. 4 • Alter the z coordinates of each vertex of “square” as follows: gl. Begin(GL_POLYGON); gl. Vertex 3 f(20. 0, gl. Vertex 3 f(80. 0, gl. Vertex 3 f(20. 0, gl. End(); 20. 0, 80. 0, 0. 5); -0. 5); 0. 1); 0. 3); • The rendering does not change, why?

Experiment 4. 5 • Add another square by inserting the following right after the code for the original square in square. cpp: gl. Begin(GL_POLYGON); gl. Vertex 3 f(120. 0, gl. Vertex 3 f(180. 0, gl. Vertex 3 f(120. 0, gl. End(); 120. 0, 180. 0, 0. 0);

Clipping • Open. GL clips the scene to within the viewing box before rendering, so that objects or parts of objects drawn outside are not rendered. • In Experiment 4. 5, can you redefine the viewing box by changing the parameters of the gl. Ortho() statement so that both squares are visible?

Experiment 4. 6 • For a more dramatic illustration of clipping, first replace the square in the original square. cpp with a triangle; in particular, replace the polygon code with the following: gl. Begin(GL_POLYGON); gl. Vertex 3 f(20. 0, 0. 0); gl. Vertex 3 f(80. 0, 0. 0); gl. End();

Experiment 4. 6 • Next, lift the first vertex up the z-axis by changing it to gl. Vertex 3 f(20. 0, 0. 5); lift it further by changing its z-value to 1. 5, then 2. 5 and, finally, 10. 0. Make sure you believe that what you see in the last three cases is indeed a triangle clipped to within the viewing box.

Screen Co-ordinates (0, 0) x Computer Screen y • So, careful about this, especially when coding programs where data is read from one system and used in the other.

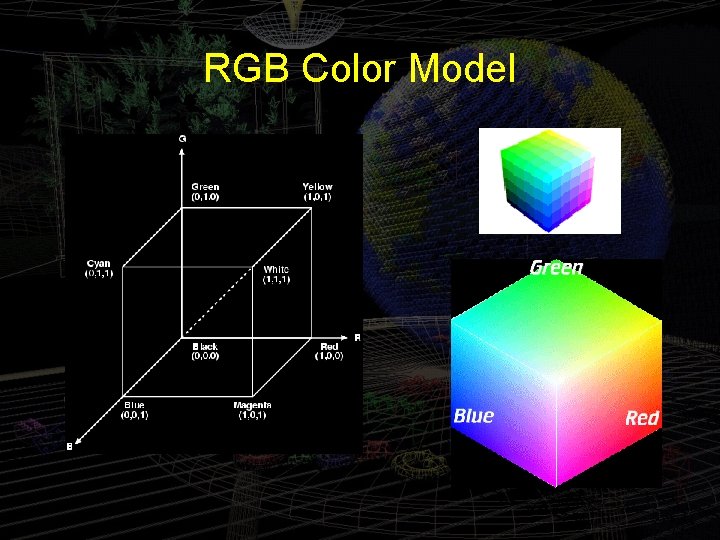
Experiment 4. 7 • The color of the square in square. cpp is specified by the three parameters of the gl. Color 3 f(0. 0, 0. 0) statement in the draw. Scene() routine, each of which gives the value of one of the three primary components, blue, green and red. • Determine which parameters to gl. Color 3 f determine the blue, green, red components. • Change parameters in gl. Clear. Color()

RGB Color Model

Experiment 4. 8 • Add the additional color declaration statement gl. Color 3 f(1. 0, 0. 0) just after the existing one gl. Color 3 f(0. 0, 0. 0) in the drawing routine of square. cpp so that the foreground color block becomes // Set foreground (or drawing) color. gl. Color 3 f(0. 0, 0. 0); gl. Color 3 f(1. 0, 0. 0);

Experiment 4. 8 • Replace the polygon declaration part of square. cpp with: gl. Begin(GL_POLYGON); gl. Color 3 f(1. 0, 0. 0); gl. Vertex 3 f(20. 0, 0. 0); gl. Color 3 f(0. 0, 1. 0, 0. 0); gl. Vertex 3 f(80. 0, 20. 0, 0. 0); gl. Color 3 f(0. 0, 1. 0); gl. Vertex 3 f(80. 0, 0. 0); gl. Color 3 f(1. 0, 0. 0); gl. Vertex 3 f(20. 0, 80. 0, 0. 0); gl. End(); • Color is a state variable.

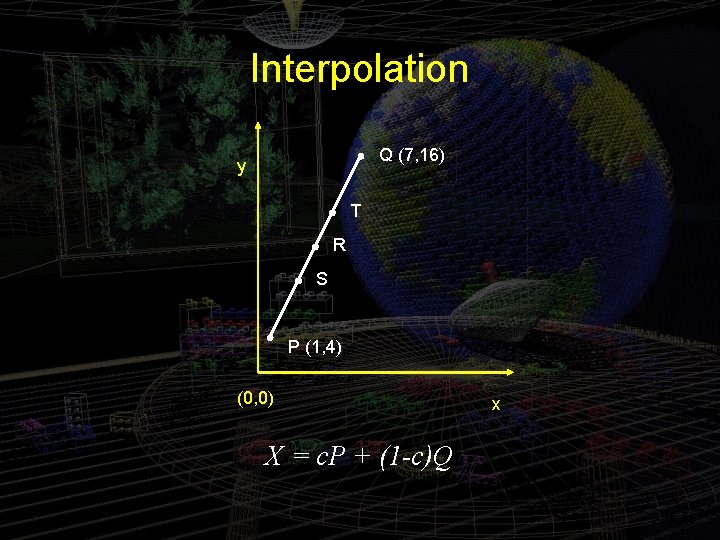
Interpolation Q (7, 16) y T R S P (1, 4) (0, 0) X = c. P + (1 -c)Q x

Exercise 4. 1 1. Modify square. cpp to draw 6 squares (red, green, blue, cyan, magenta, and yellow) on the white background as: (in class)

Exercise 4. 2 2. Modify square. cpp to draw one Equilateral, one Isosceles, one Scalene, and one Right triangles with different colors. (in class)

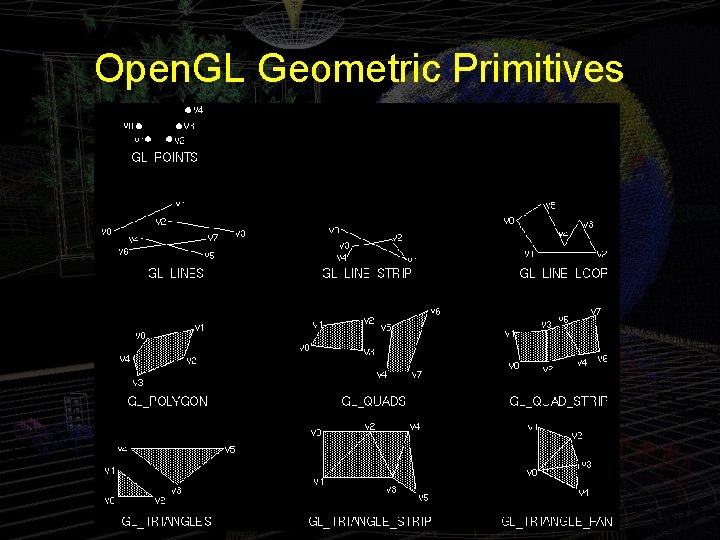
Open. GL Geometric Primitives

Experiment 4. 9 • Replace gl. Begin(GL_POLYGON) with gl. Begin(GL_POINTS) in square. cpp and make the point size bigger by inserting // Set point size gl. Point. Size(5. 0); just before gl. Begin(GL_POINTS) • Continue, replacing GL_POINTS with GL_LINES, GL_LINE_STRIP and, GL_LINE_LOOP. • The thickness of lines can be set by a gl. Line. Width(width) call.

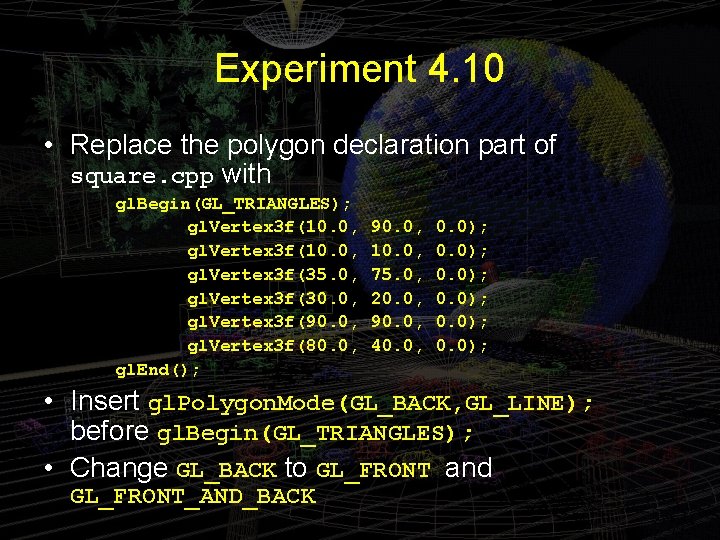
Experiment 4. 10 • Replace the polygon declaration part of square. cpp with gl. Begin(GL_TRIANGLES); gl. Vertex 3 f(10. 0, gl. Vertex 3 f(35. 0, gl. Vertex 3 f(30. 0, gl. Vertex 3 f(90. 0, gl. Vertex 3 f(80. 0, gl. End(); 90. 0, 10. 0, 75. 0, 20. 0, 90. 0, 40. 0, 0. 0); • Insert gl. Polygon. Mode(GL_BACK, GL_LINE); before gl. Begin(GL_TRIANGLES); • Change GL_BACK to GL_FRONT and GL_FRONT_AND_BACK

Experiment 4. 11 • Replace the polygon declaration part of square. cpp with gl. Polygon. Mode(GL_FRONT_AND_BACK, GL_LINE); gl. Begin(GL_TRIANGLE_STRIP); gl. Color 3 f(1. 0, 0. 0); gl. Vertex 3 f(10. 0, 90. 0, 0. 0); gl. Color 3 f(0. 0, 1. 0, 0. 0); gl. Vertex 3 f(10. 0, 0. 0); gl. Color 3 f(0. 0, 1. 0); gl. Vertex 3 f(35. 0, 75. 0, 0. 0); gl. Color 3 f(1. 0, 0. 0); gl. Vertex 3 f(30. 0, 20. 0, 0. 0); gl. Color 3 f(1. 0, 0. 0, 1. 0); gl. Vertex 3 f(90. 0, 0. 0); gl. Color 3 f(0. 0, 1. 0); gl. Vertex 3 f(80. 0, 40. 0, 0. 0); gl. End();

Experiment 4. 12 • Replace GL_FRONT_AND_BACK in the previous experiment with GL_FRONT and GL_BACK • Replace the polygon declaration part of square. cpp with gl. Begin(GL_TRIANGLE_FAN); gl. Vertex 3 f(10. 0, gl. Vertex 3 f(15. 0, 90. 0, gl. Vertex 3 f(55. 0, 75. 0, gl. Vertex 3 f(80. 0, 30. 0, gl. Vertex 3 f(90. 0, 10. 0, gl. End(); 0. 0); • Apply both the filled and outlined drawing modes.

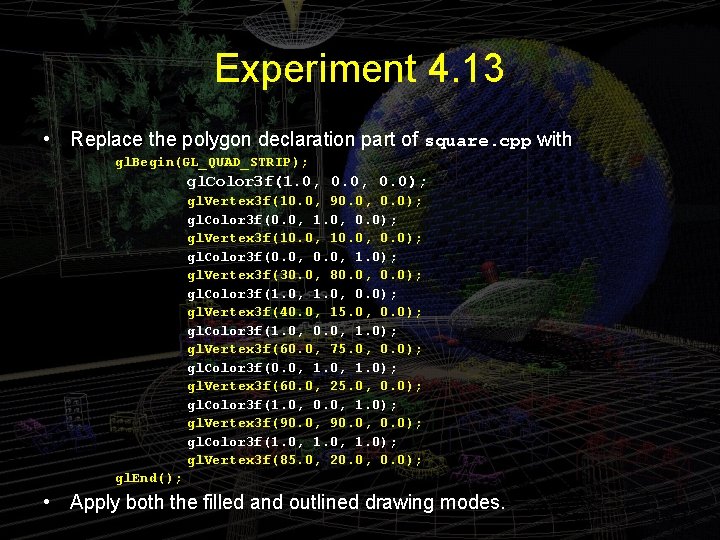
Experiment 4. 13 • Replace the polygon declaration part of square. cpp with gl. Begin(GL_QUAD_STRIP); gl. Color 3 f(1. 0, 0. 0); gl. Vertex 3 f(10. 0, 90. 0, 0. 0); gl. Color 3 f(0. 0, 1. 0, 0. 0); gl. Vertex 3 f(10. 0, 0. 0); gl. Color 3 f(0. 0, 1. 0); gl. Vertex 3 f(30. 0, 80. 0, 0. 0); gl. Color 3 f(1. 0, 0. 0); gl. Vertex 3 f(40. 0, 15. 0, 0. 0); gl. Color 3 f(1. 0, 0. 0, 1. 0); gl. Vertex 3 f(60. 0, 75. 0, 0. 0); gl. Color 3 f(0. 0, 1. 0); gl. Vertex 3 f(60. 0, 25. 0, 0. 0); gl. Color 3 f(1. 0, 0. 0, 1. 0); gl. Vertex 3 f(90. 0, 0. 0); gl. Color 3 f(1. 0, 1. 0); gl. Vertex 3 f(85. 0, 20. 0, 0. 0); gl. End(); • Apply both the filled and outlined drawing modes.

Experiment 4. 14 • Replace GL_QUAD_STRIP in the previous experiment with GL_QUADS and GL_POLYGON • Try to change some vertices, to make the polygon lines not cross to each other. • Apply both the filled and outlined drawing modes.

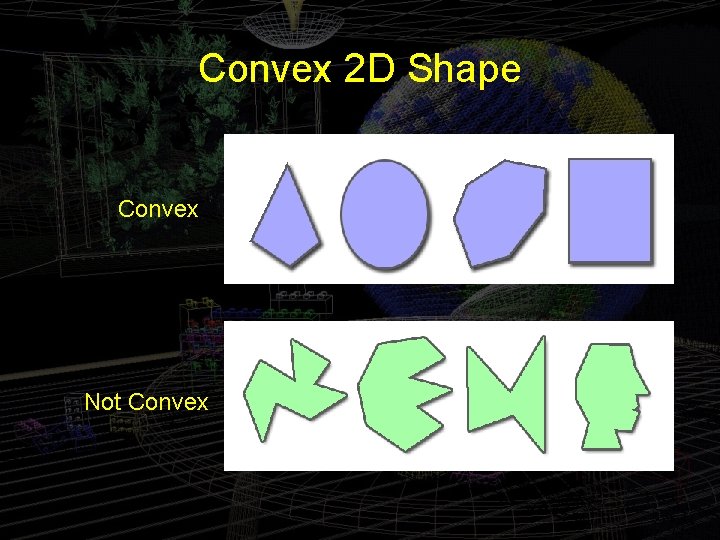
(Extremely) Important Note • When specifying triangles in Open. GL, ensure that contiguous triangles are consistently oriented. • Also ensure when using GL_QUADS, GL_QUAD_STRIP or GL_POLYGON that each polygon is a plane convex figure.

Convex 2 D Shape Convex Not Convex

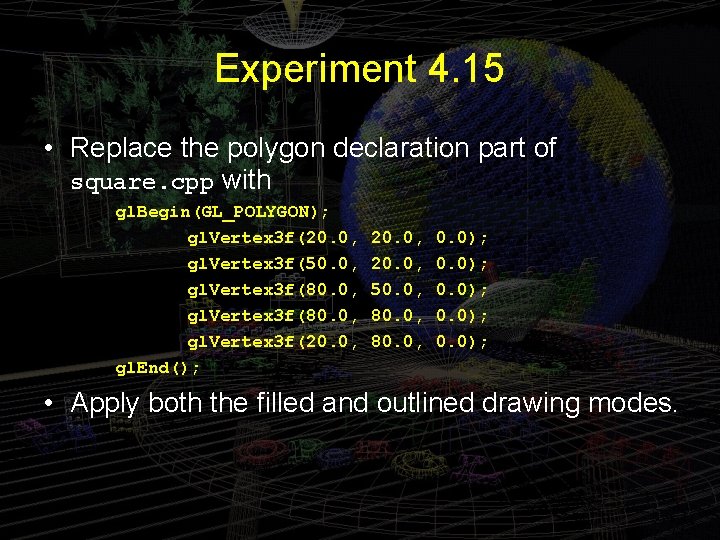
Experiment 4. 15 • Replace the polygon declaration part of square. cpp with gl. Begin(GL_POLYGON); gl. Vertex 3 f(20. 0, gl. Vertex 3 f(50. 0, gl. Vertex 3 f(80. 0, gl. Vertex 3 f(20. 0, gl. End(); 20. 0, 50. 0, 80. 0, 0. 0); • Apply both the filled and outlined drawing modes.

Experiment 4. 16 • Replace the polygon declaration part of square. cpp with gl. Begin(GL_POLYGON); gl. Vertex 3 f(20. 0, gl. Vertex 3 f(80. 0, gl. Vertex 3 f(40. 0, gl. Vertex 3 f(20. 0, gl. End(); 20. 0, 40. 0, 80. 0, 0. 0); • Apply both the filled and outlined drawing modes.

Experiment 4. 16 • Draw the same shape, but change the sequence, move the first vertex to the last vertex as. gl. Begin(GL_POLYGON); gl. Vertex 3 f(80. 0, gl. Vertex 3 f(40. 0, gl. Vertex 3 f(20. 0, gl. End(); 20. 0, 40. 0, 80. 0, 20. 0, 0. 0); • Apply both the filled and outlined drawing modes. • What happened? Why?

Approximating Curved Objects • There is no Open. GL primitive objects for curves, or circles. • Sincerity is a very important human quality. If you don’t have it, you gotta fake it!!” y p r t (h, k) p = (h + rcos(t), k + rsin(t)) x

Experiment 4. 17 • Run circle. cpp. Increase the number of vertices on the line loop by pressing ‘+’ till it “becomes” a circle. Press ‘-’ to decrease the number of vertices. • Draw a disc (a filled circle) by way of – A polygon – A triangle fan.

Experiment 4. 18 • Run parabola. cpp. Increase the number of vertices on the line strip by pressing ‘+’ and decrease the number of vertices by pressing ‘-’. • The parametric equations implemented are x = 50 + 50 t, y = 100 t 2, -1 <= t <= 1 • Try to modify the equation.

Assignment 1 1. Modify square. cpp to draw a Pythagoras diagram (the diagram must be accurate).

Assignment 1 2. Create a square annulus (a) using a single triangular strip (in class). 3. Create a shape (b) using a single triangular strip. 4. Create a square annulus (a) using two triangle fans. (a) (b)

Assignment 1 5. Draw a sine curve between x = -p and x = p. 6. Draw an ellipse. Recall the parametric equations for an ellipse with semi-major axis of length A and semi-minor of length B. y (h, k + B) p = (h + Acos(t), k + Bsin(t)), 0 £ t £ p r t (h, k) x (h + A, k)

Assignment 1 7. Modify square. cpp or circle. cpp to draw a house. Please feel free to use your imagination.