On the Optimality and Interconnection of VLB Networks

On the Optimality and Interconnection of VLB Networks Moshe Babaioff and John Chuang UC Berkeley IEEE INFOCOM 2007 Anchorage, Alaska, USA May 8, 2007 Clean Slate Project Babaioff & Chuang 2007

Main Points • Universal optimality of Valiant Load Balancing (VLB) network under node failures (in paper) • Interconnection of multiple VLB networks – Interconnection challenges – Generalization: m-hubs VLB – Support peering and transit relationships 2 Clean Slate Project Babaioff & Chuang 2007

Backbone Network Design r r 1 n r 2 r 3 Network? … 4 r r • Many challenges: – Traffic matrix can change over short and long timescales – Customers expect high availability and low congestion – Network operator must design for low congestion and high fault tolerance over the lifetime of the network 3 Clean Slate Project Babaioff & Chuang 2007

Valiant Load-Balancing (VLB) [Zhang-Shen & Mc. Keown; Kodialam et. al. ] • Clean-slate approach to backbone design: – Design a network that supports any legal traffic matrix (fij)i, j • Input: – n : the number of nodes – r : bound on each node’s ingress and egress rates (hose model) • Output: A network that supports any legal traffic matrix on the n nodes: – Capacity cij on each edge (i, j) – A routing scheme that respects the edge capacities 4 Clean Slate Project Babaioff & Chuang 2007

Valiant Load-Balancing (VLB) [Zhang-Shen & Mc. Keown] • fij : rate from i to j • Σj fij ≤r , Σi fij ≤r • Two-stage routing of fij : • i sends fij/n to each node k • k forwards to j 1 1 2 n r … 4 • For any legal traffic matrix, flow of at most: Σj fij/n ≤r/n per stage per edge • Total capacity: 2 r(n-1) is optimal • Additional results for heterogeneous nodes, fault tolerance 2 r/n 3 r r 5 Clean Slate Project Babaioff & Chuang 2007

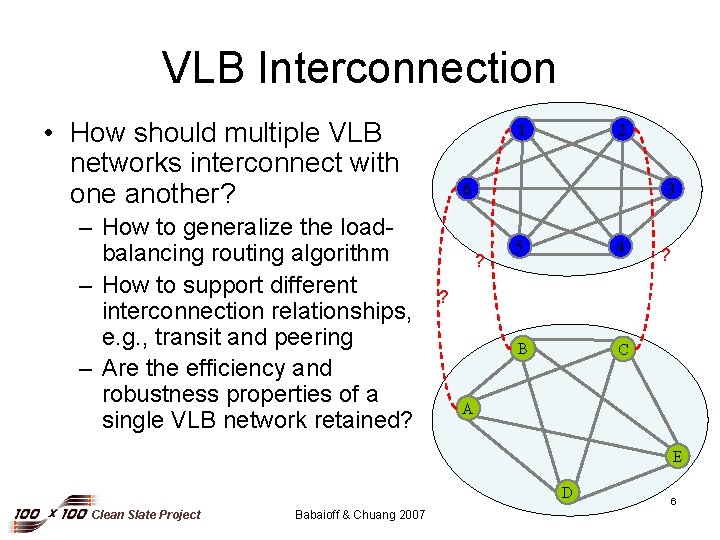
VLB Interconnection • How should multiple VLB networks interconnect with one another? – How to generalize the loadbalancing routing algorithm – How to support different interconnection relationships, e. g. , transit and peering – Are the efficiency and robustness properties of a single VLB network retained? 1 2 6 3 ? 5 4 B C ? ? A E D Clean Slate Project Babaioff & Chuang 2007 6

VLB Generalization: m-hubs VLB • Each stream is equally loadbalanced on m nodes (the hubs) – n-hubs = VLB – 1 -hub = star r/m r/m 2 r/m • Fact: any m-hubs network can support any legal traffic matrix, and it has optimal network capacity of 2 r(n-1). Capacity: 2(n-m)m (r/m) + m(m-1) (2 r/m) = 2 r(n-1) 7 Clean Slate Project Babaioff & Chuang 2007

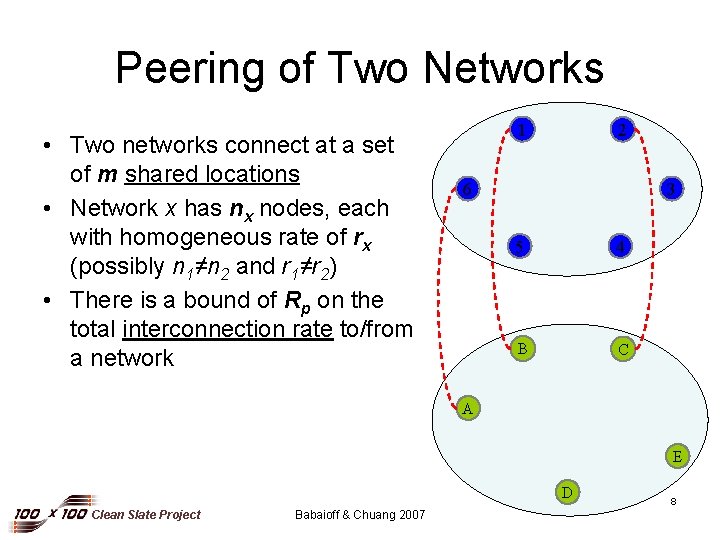
Peering of Two Networks • Two networks connect at a set of m shared locations • Network x has nx nodes, each with homogeneous rate of rx (possibly n 1≠n 2 and r 1≠r 2) • There is a bound of Rp on the total interconnection rate to/from a network 1 2 6 3 5 4 B C A E D Clean Slate Project Babaioff & Chuang 2007 8

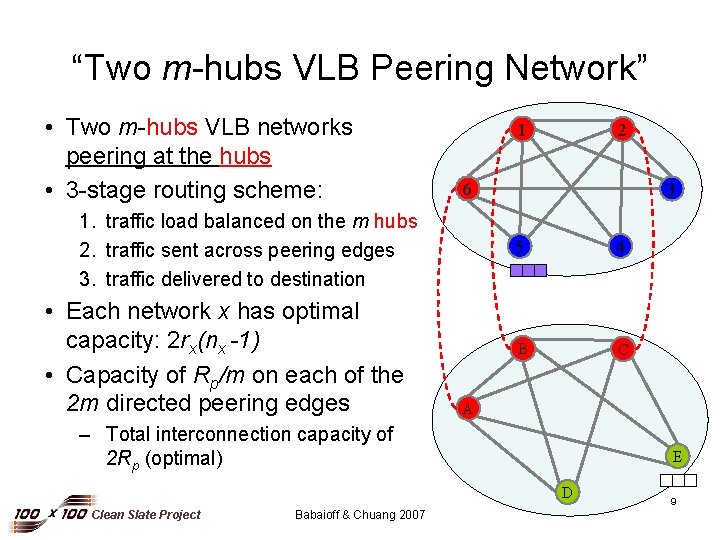
“Two m-hubs VLB Peering Network” • Two m-hubs VLB networks peering at the hubs • 3 -stage routing scheme: 1 6 1. traffic load balanced on the m hubs 2. traffic sent across peering edges 3. traffic delivered to destination • Each network x has optimal capacity: 2 rx(nx -1) • Capacity of Rp/m on each of the 2 m directed peering edges 2 3 5 4 B C A – Total interconnection capacity of 2 Rp (optimal) E D Clean Slate Project Babaioff & Chuang 2007 9

Peering of 2 Networks: Results Theorem: The “two m-hubs VLB peering network” can support any legal traffic matrix and has minimal capacity in each network and minimal interconnection capacity. • Result extends to q>2 networks in the case of universally shared locations: all networks share m>0 locations • Extension to node failures 10 Clean Slate Project Babaioff & Chuang 2007

Interconnection without Universally Shared Locations • With three or more VLB networks, it may be infeasible to require a set of interconnection points universally shared by all networks – – Networks have different coverage areas Raises entry barrier for new networks; reduces evolvability • Consider alternate VLB interconnection schemes – – Transit vs. peering schemes Note: routing stages will have to increase 11 Clean Slate Project Babaioff & Chuang 2007

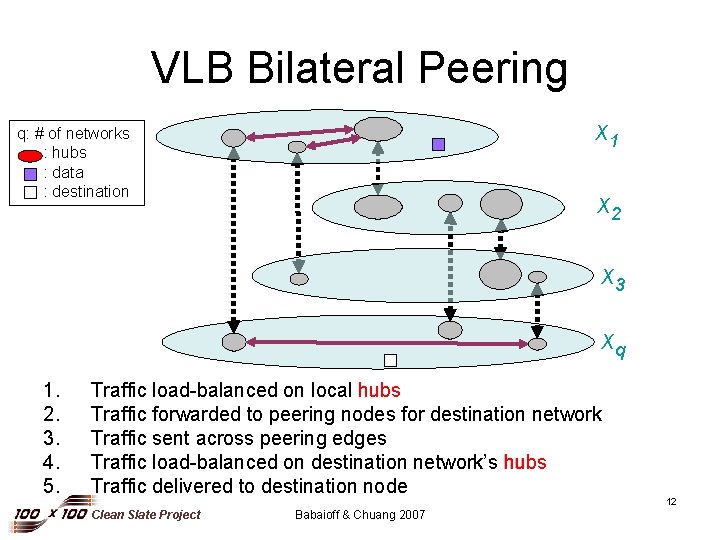
VLB Bilateral Peering x 1 q: # of networks : hubs : data : destination x 2 x 3 xq 1. 2. 3. 4. 5. Traffic load-balanced on local hubs Traffic forwarded to peering nodes for destination network Traffic sent across peering edges Traffic load-balanced on destination network’s hubs Traffic delivered to destination node Clean Slate Project Babaioff & Chuang 2007 12

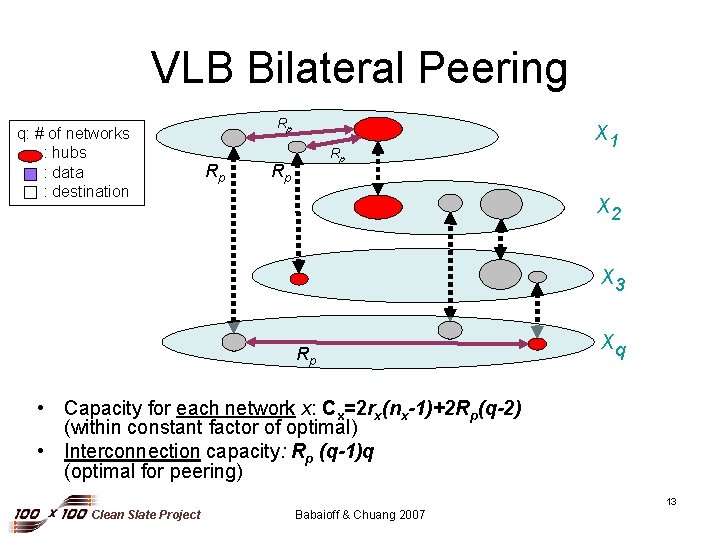
VLB Bilateral Peering q: # of networks : hubs : data : destination Rp Rp x 1 x 2 x 3 Rp xq • Capacity for each network x: Cx=2 rx(nx-1)+2 Rp(q-2) (within constant factor of optimal) • Interconnection capacity: Rp (q-1)q (optimal for peering) 13 Clean Slate Project Babaioff & Chuang 2007

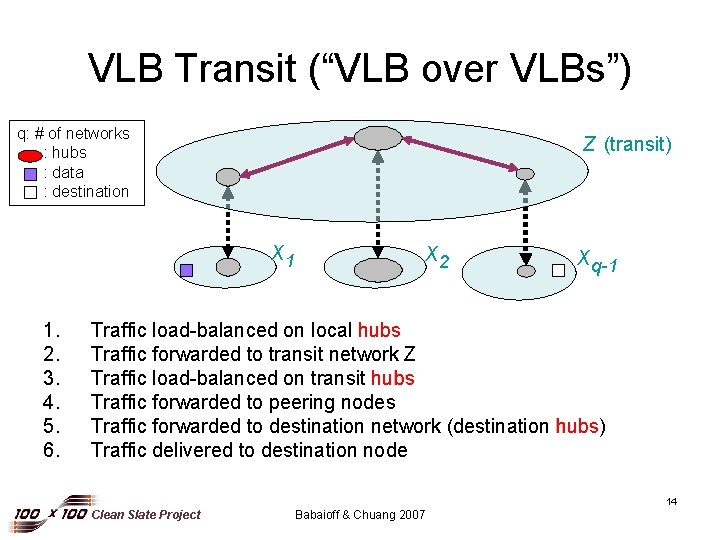
VLB Transit (“VLB over VLBs”) q: # of networks : hubs : data : destination z (transit) x 1 1. 2. 3. 4. 5. 6. x 2 xq-1 Traffic load-balanced on local hubs Traffic forwarded to transit network Z Traffic load-balanced on transit hubs Traffic forwarded to peering nodes Traffic forwarded to destination network (destination hubs) Traffic delivered to destination node 14 Clean Slate Project Babaioff & Chuang 2007

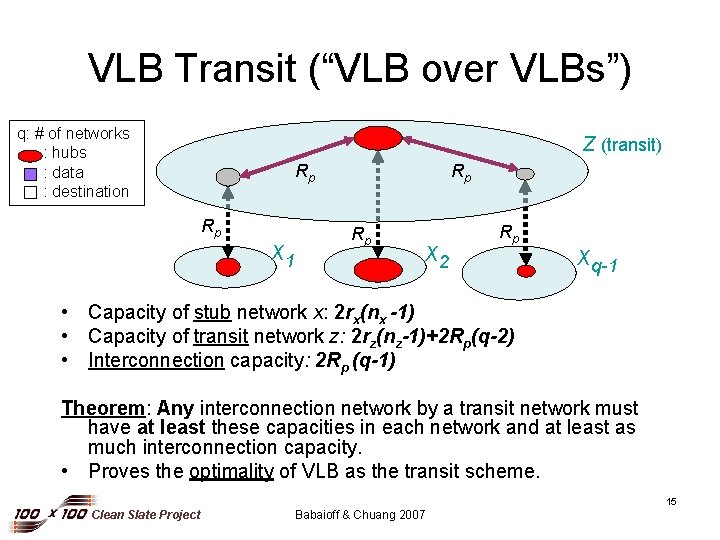
VLB Transit (“VLB over VLBs”) q: # of networks : hubs : data : destination z (transit) Rp Rp x 1 Rp Rp x 2 Rp xq-1 • Capacity of stub network x: 2 rx(nx -1) • Capacity of transit network z: 2 rz(nz-1)+2 Rp(q-2) • Interconnection capacity: 2 Rp (q-1) Theorem: Any interconnection network by a transit network must have at least these capacities in each network and at least as much interconnection capacity. • Proves the optimality of VLB as the transit scheme. 15 Clean Slate Project Babaioff & Chuang 2007

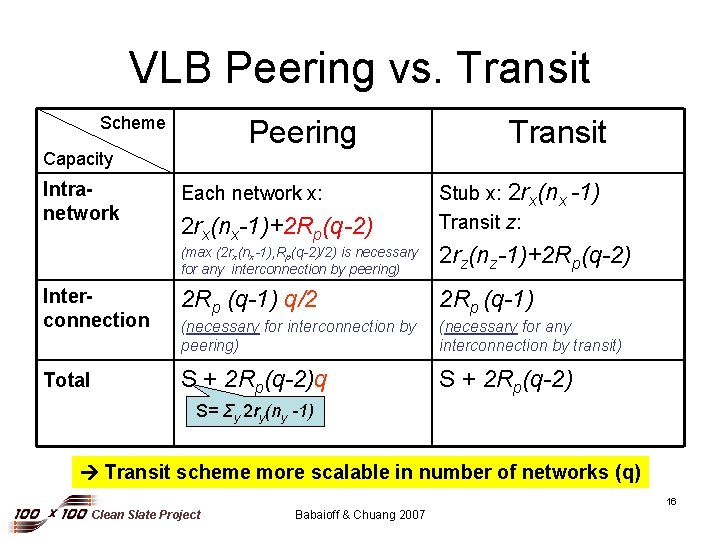
VLB Peering vs. Transit Scheme Peering Capacity Intranetwork Each network x: 2 rx(nx-1)+2 Rp(q-2) Transit Stub x: 2 rx(nx -1) Transit z: (max (2 rx(nx-1), Rp(q-2)/2) is necessary for any interconnection by peering) 2 rz(nz-1)+2 Rp(q-2) Interconnection 2 Rp (q-1) q/2 2 Rp (q-1) (necessary for interconnection by peering) (necessary for any interconnection by transit) Total S + 2 Rp(q-2)q S + 2 Rp(q-2) S= Σy 2 ry(ny -1) Transit scheme more scalable in number of networks (q) 16 Clean Slate Project Babaioff & Chuang 2007

Summary • Established universal optimality of VLB under node failures (not presented today) • Generalized m-hubs VLB network serves as building block for VLB interconnection – m-hubs VLB design retains desirable properties of VLB while allowing diverse VLB networks to interconnect – Can support both peering and transit relationships – Established optimality for VLB transit, and within constant factor of optimality for VLB peering • Open questions: – Support simultaneous transit and peering – Fault tolerance: failure of nodes, edges, transit networks – Strategic interaction between VLB networks 17 Clean Slate Project Babaioff & Chuang 2007