On the Importance of Synchronization Primitives with Low








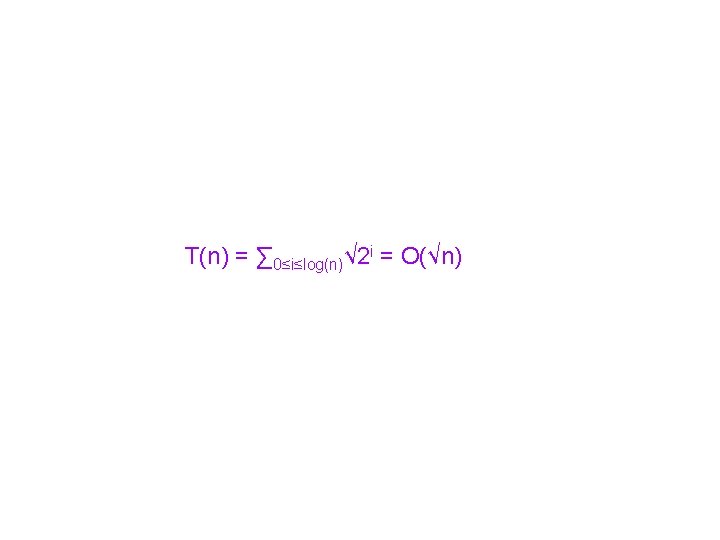


- Slides: 48

On the Importance of Synchronization Primitives with Low Consensus Numbers Pankaj Khanchandani, Roger Wattenhofer Distributed Computing Group (DISCO) ETH Zurich

Multiprocessor machines with 100+ hardware threads such Intel Xeon or AMD Epyc are quite common now.

0 1 2 3 4

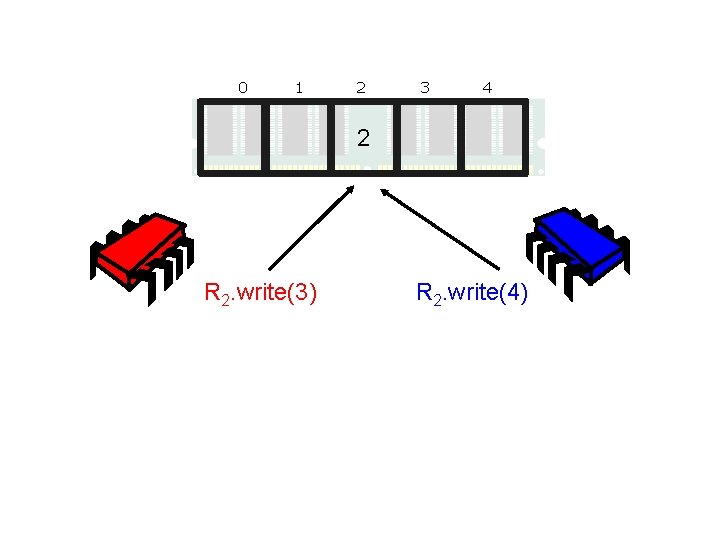
0 1 2 3 4 2 R 2. write(3) R 2. write(4)

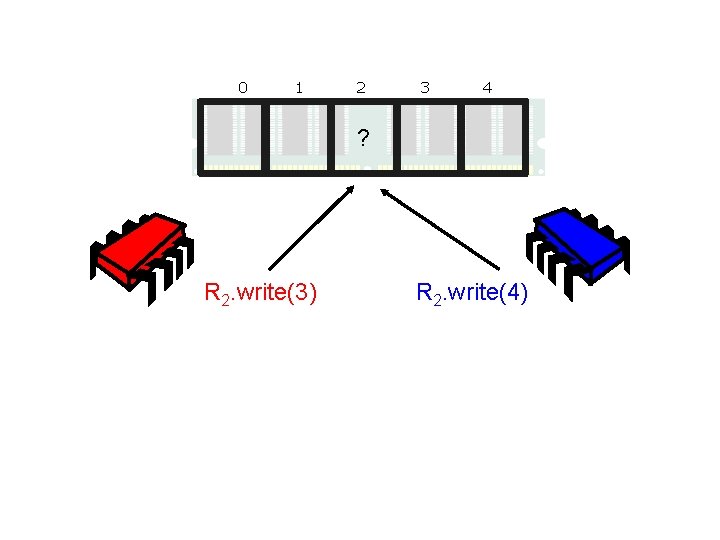
0 1 2 3 4 ? R 2. write(3) R 2. write(4)

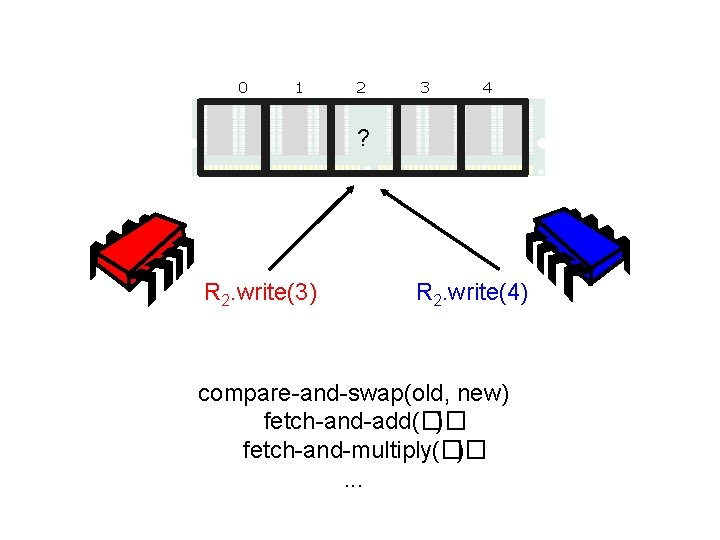
0 1 2 3 4 ? R 2. write(3) R 2. write(4) compare-and-swap(old, new) fetch-and-add(�� ) fetch-and-multiply(�� ). . .

Synchronization Power = Consensus Number compare-and-swap ∞ fetch-and-add 2 fetch-and-multiply 2 read, write 1 A read-modify-write instruction with consensus number n can solve any synchronization task among n processes [Herlihy 1991].

Status Quo: Compare-and-swap is widely supported and used for solving synchronization tasks. Our Claim: Ignoring low consensus number synchronization primitives can be very inefficient.

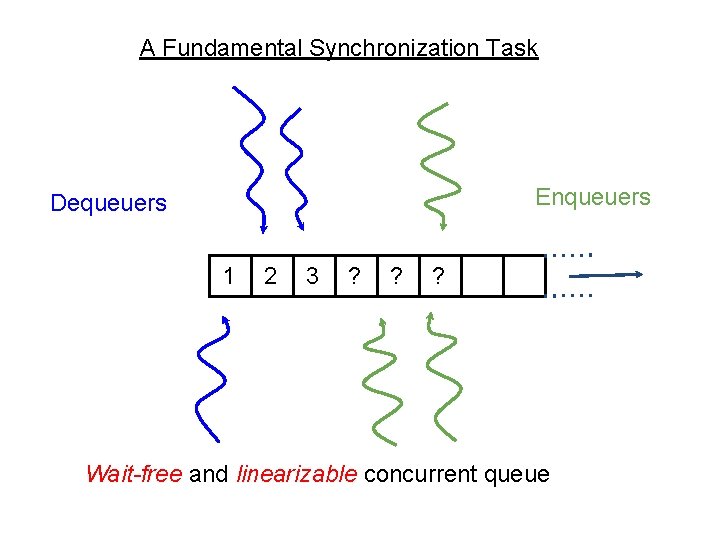
A Fundamental Synchronization Task Enqueuers Dequeuers 1 2 3 ? ? ? Wait-free and linearizable concurrent queue

Our Contribution Improving the runtime of wait-free and linearizable concurrent queue using low consensus number primitives. Known: compare-and-swap O(n) New: compare-and-swap + half-max (c. n. 1) + O(√n) half-increment (c. n. 2) combining low consensus number instructions [Ellen et al. 2016]

Wait-free and linearizable concurrent queue using the following register operations enqueue(�� ) 1. read() 1. write(�� ) 1. compare-and-swap(�� , �� ) ∞ 1. half-increment() 2 1. half-max(�� ) 1 dequeue()

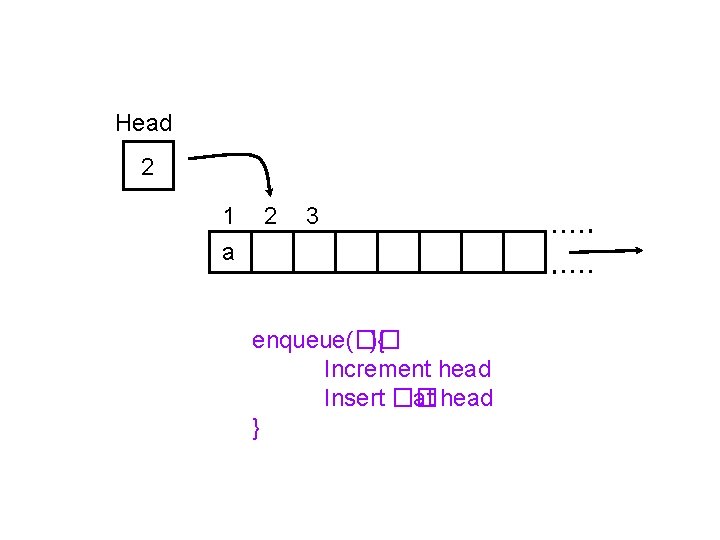
Head 2 1 a 2 3 enqueue(�� ){ Increment head Insert �� at head }

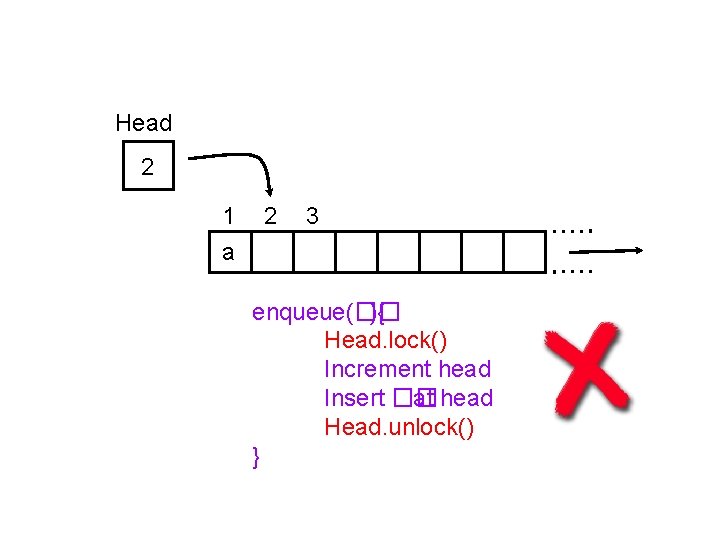
Head 2 1 a 2 3 enqueue(�� ){ Head. lock() Increment head Insert �� at head Head. unlock() }

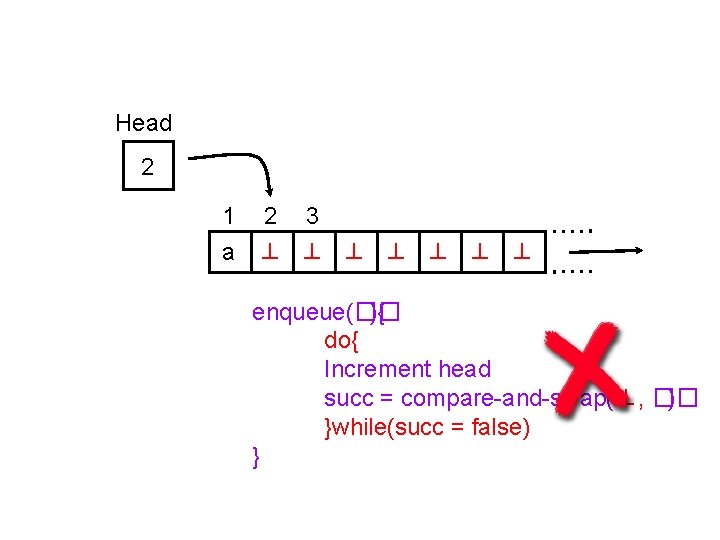
Head 2 1 2 3 a ⊥ ⊥ ⊥ ⊥ enqueue(�� ){ do{ Increment head succ = compare-and-swap(⊥, �� ) }while(succ = false) }

Queue Design in Two Steps Queue for at most n pending enqueue operations (Counting Set) Queue for all the enqueue operations

Counting Set 1. insert(�� ): inserts �� and returns the # of insert operations completed. 2. remove(i): removes and returns the ith inserted element if it was not already removed o. w. returns ⊥. 3. Stores at most one element per process. Operation Return Set {⊥, ⊥} 1 P 1. insert(a) {a, ⊥} 2 P 2. insert(b) {a, b} b P 1. remove(2) {a, ⊥} ⊥ {a, ⊥}

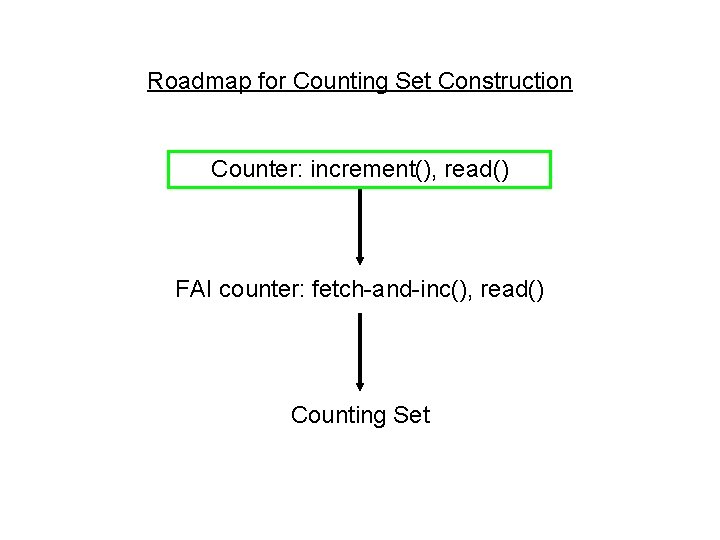
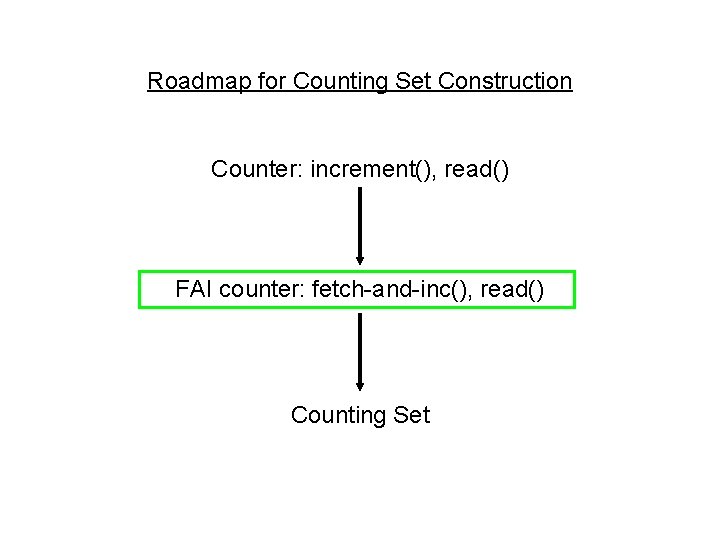
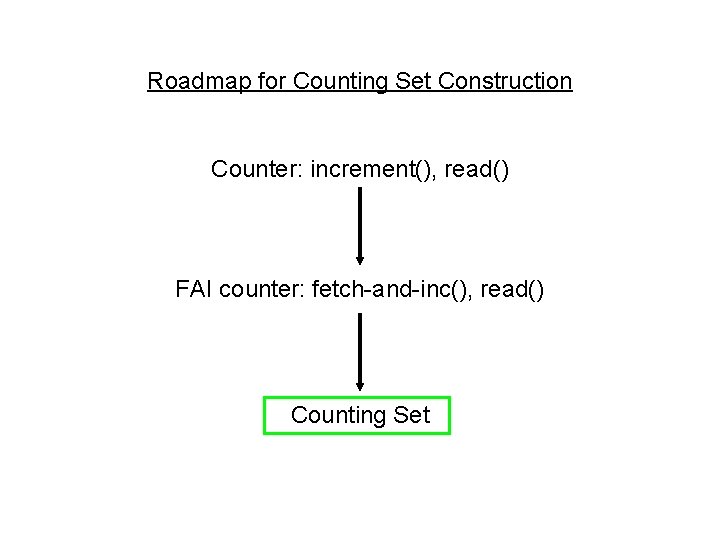
Roadmap for Counting Set Construction Counter: increment(), read() FAI counter: fetch-and-inc(), read() Counting Set

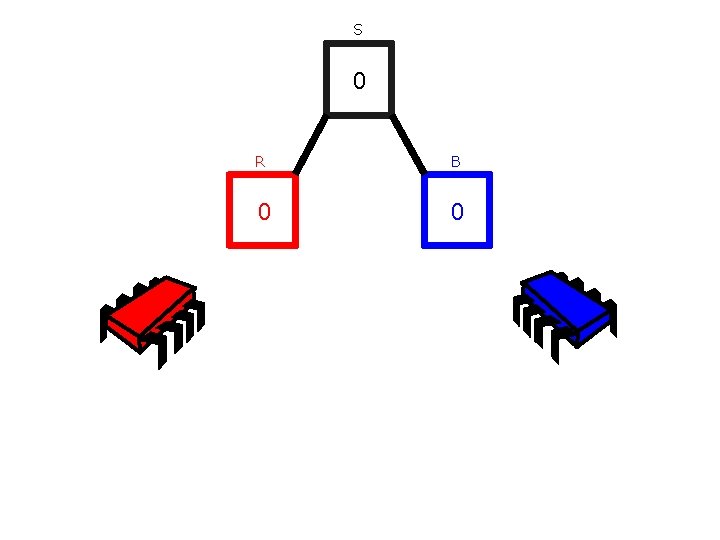
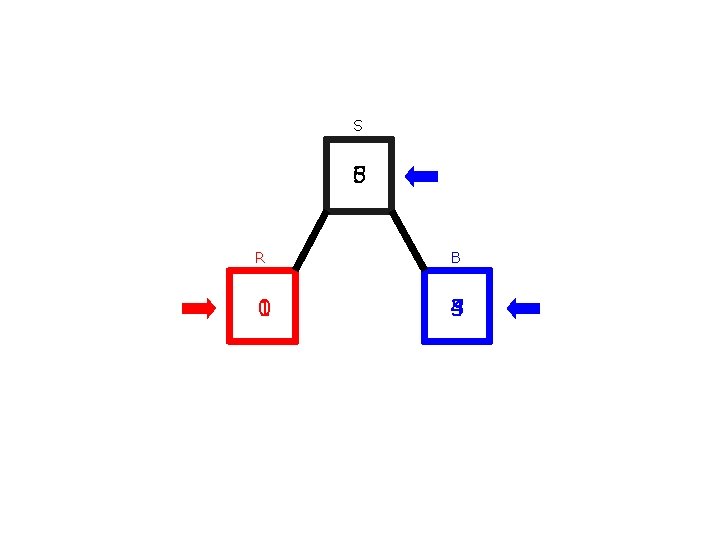
S 0 R B 0 0

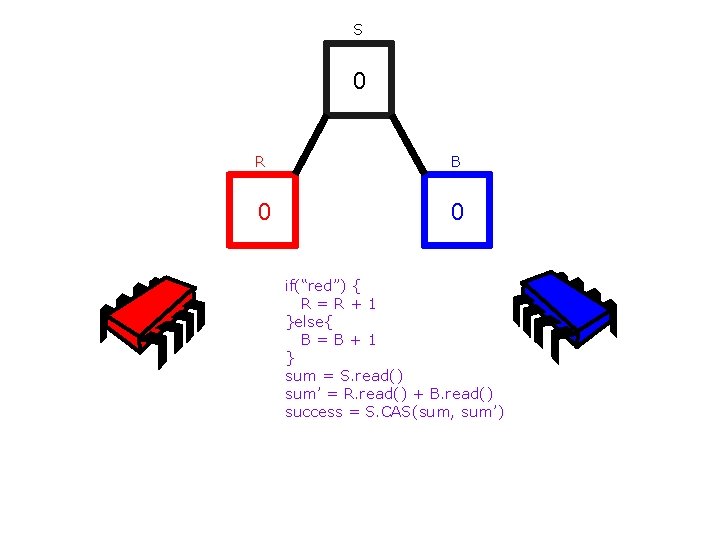
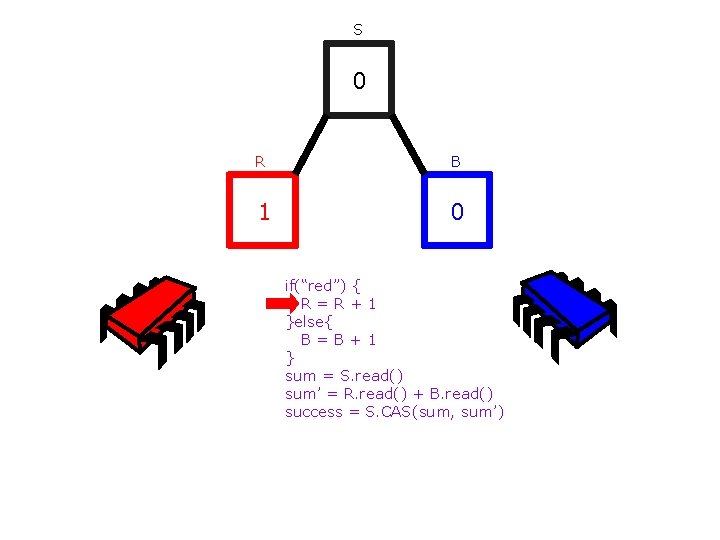
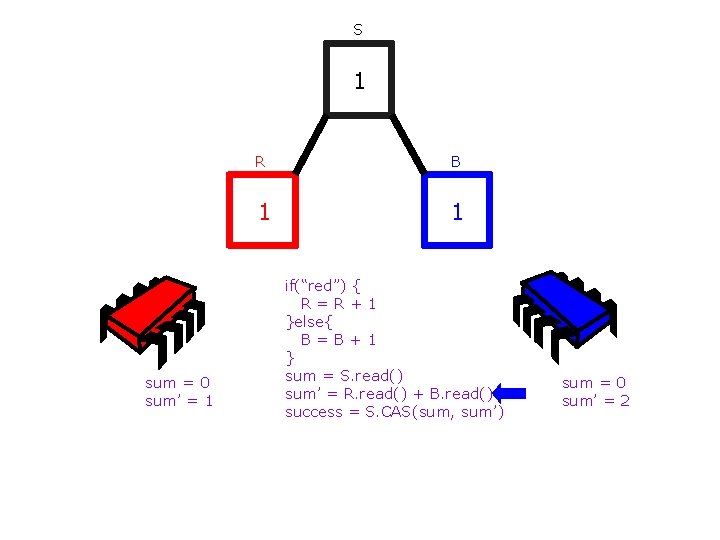
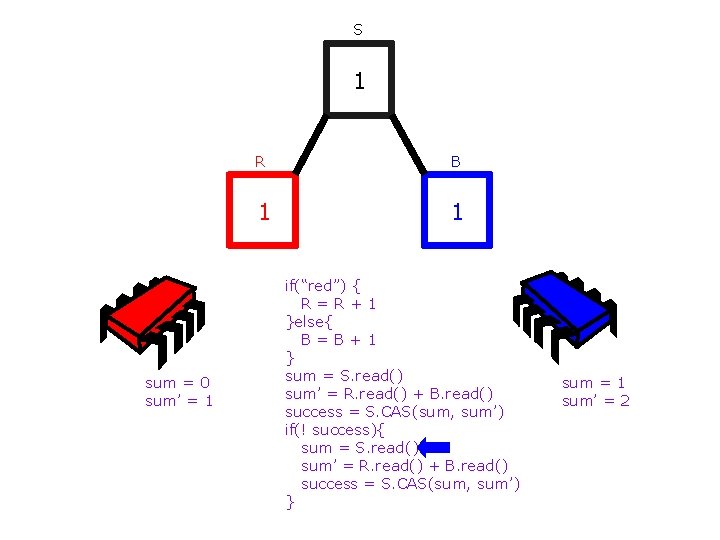
S 0 R B 0 0 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’)

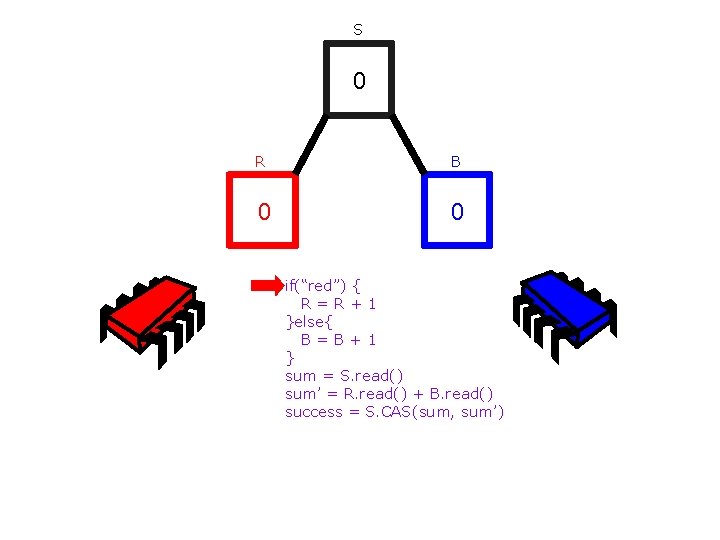
S 0 R B 0 0 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’)

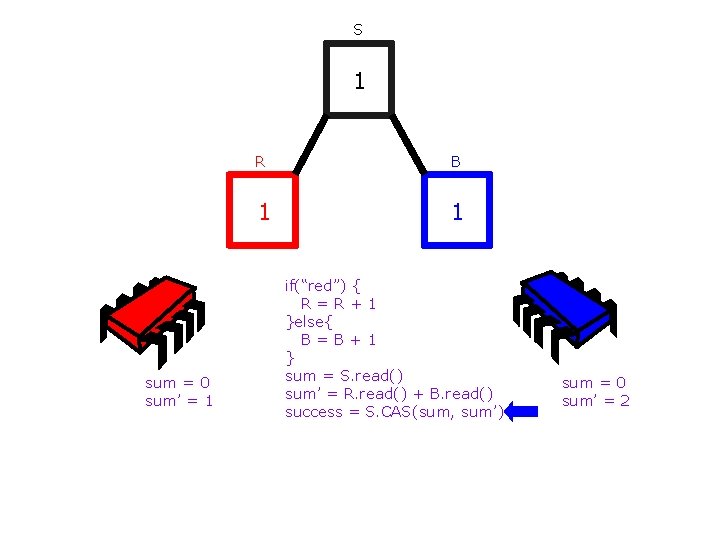
S 0 R B 1 0 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’)

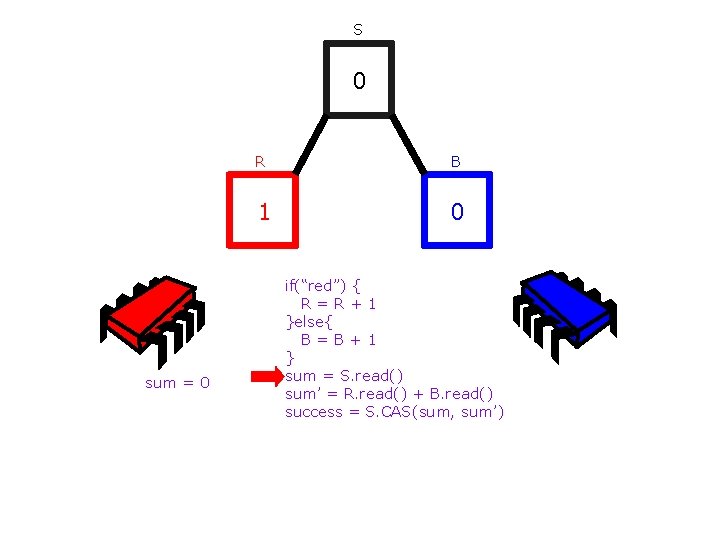
S 0 sum = 0 R B 1 0 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’)

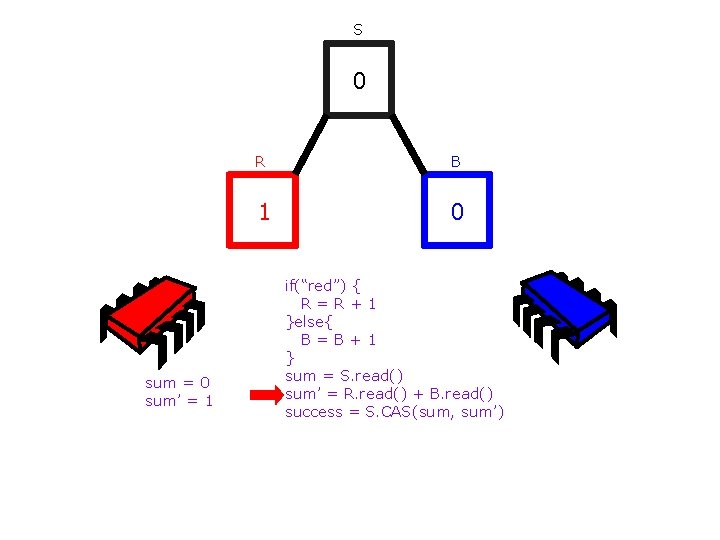
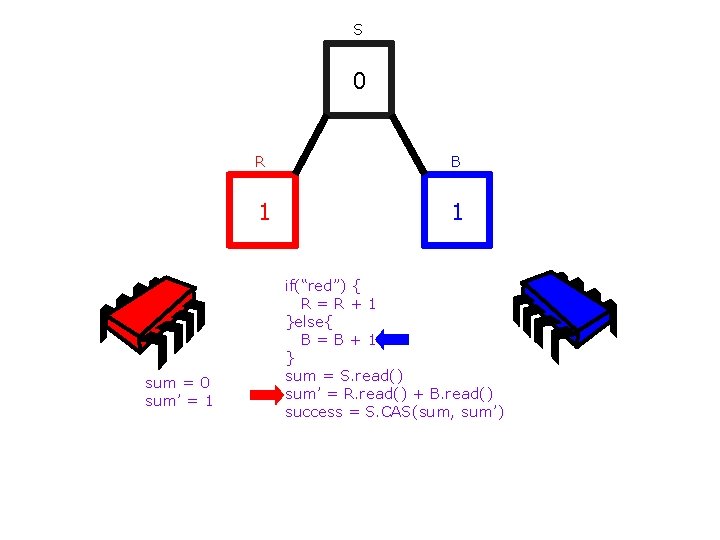
S 0 sum = 0 sum’ = 1 R B 1 0 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’)

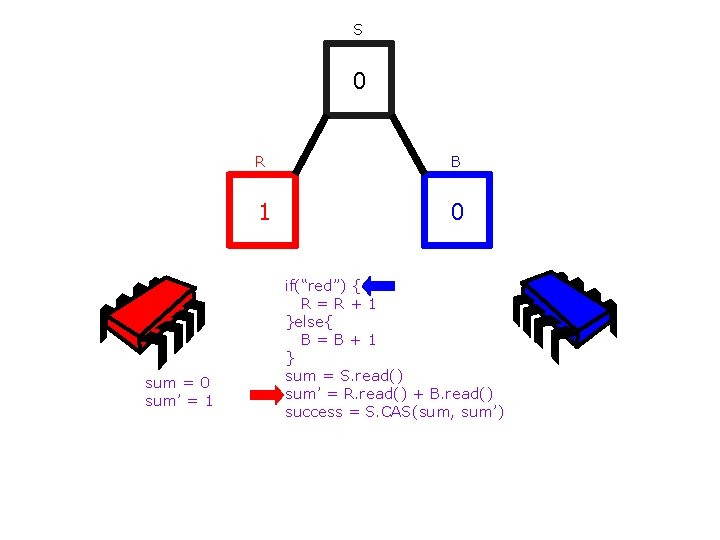
S 0 sum = 0 sum’ = 1 R B 1 0 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’)

S 0 sum = 0 sum’ = 1 R B 1 1 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’)

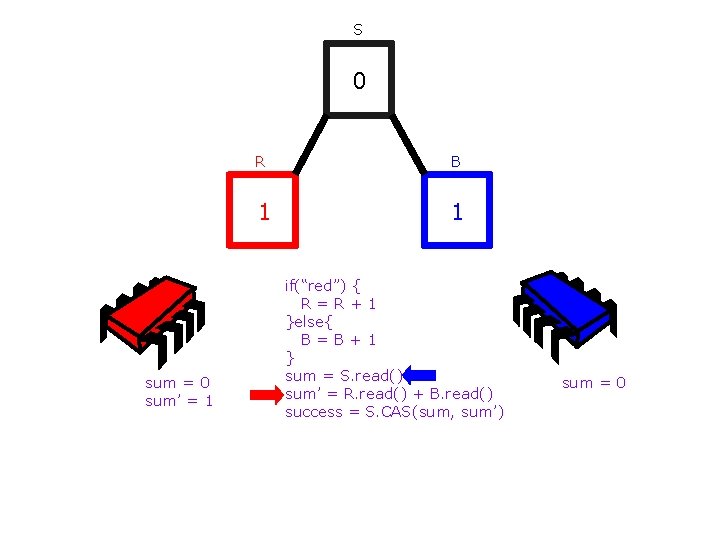
S 0 sum = 0 sum’ = 1 R B 1 1 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) sum = 0

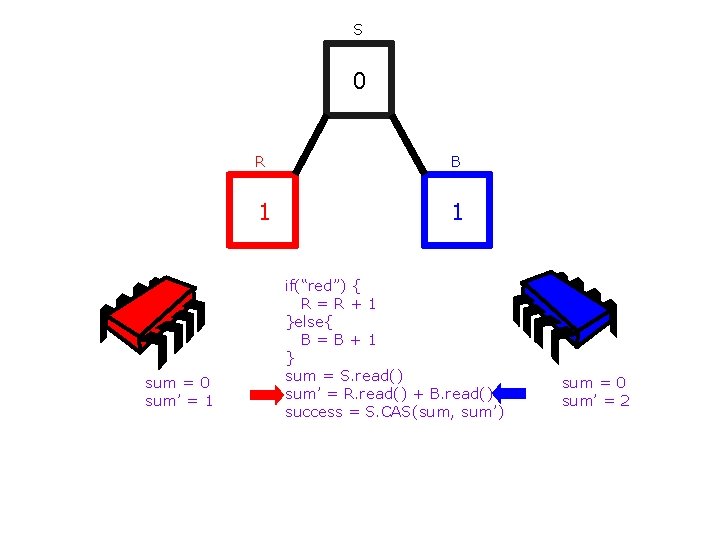
S 0 sum = 0 sum’ = 1 R B 1 1 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) sum = 0 sum’ = 2

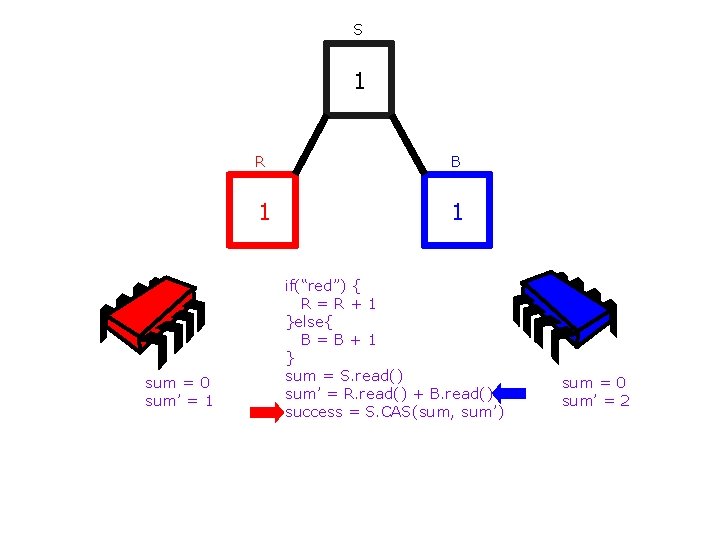
S 1 sum = 0 sum’ = 1 R B 1 1 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) sum = 0 sum’ = 2

S 1 sum = 0 sum’ = 1 R B 1 1 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) sum = 0 sum’ = 2

S 1 sum = 0 sum’ = 1 R B 1 1 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) sum = 0 sum’ = 2

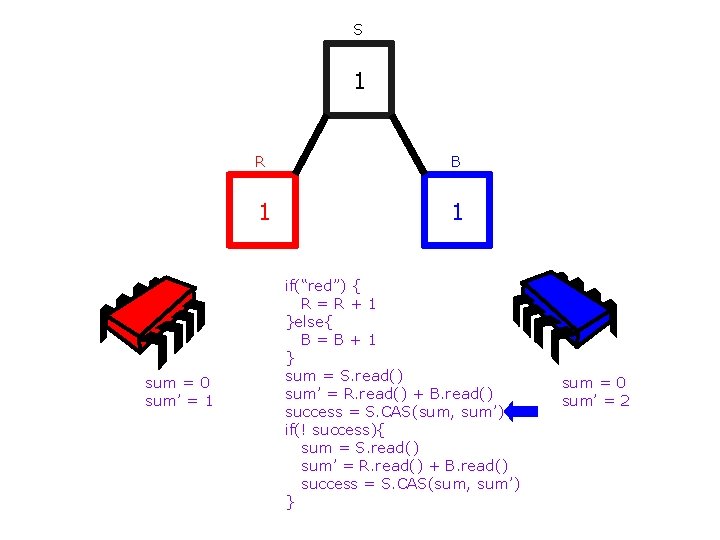
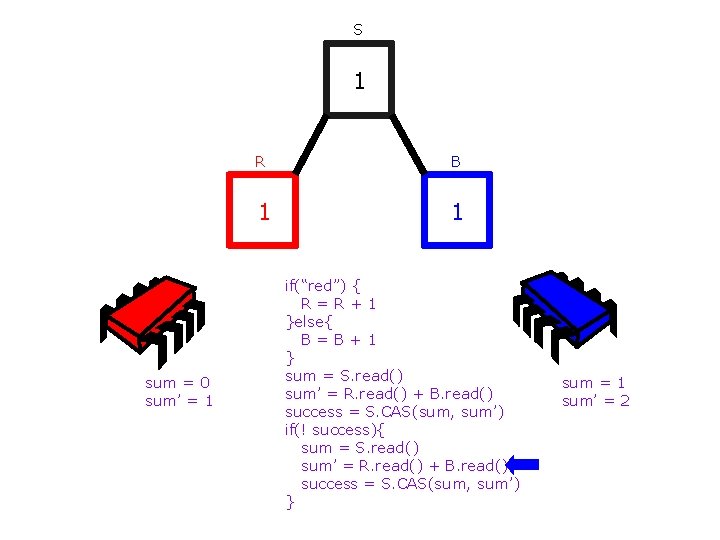
S 1 sum = 0 sum’ = 1 R B 1 1 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) if(! success){ sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) } sum = 0 sum’ = 2

S 1 sum = 0 sum’ = 1 R B 1 1 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) if(! success){ sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) } sum = 0 sum’ = 2

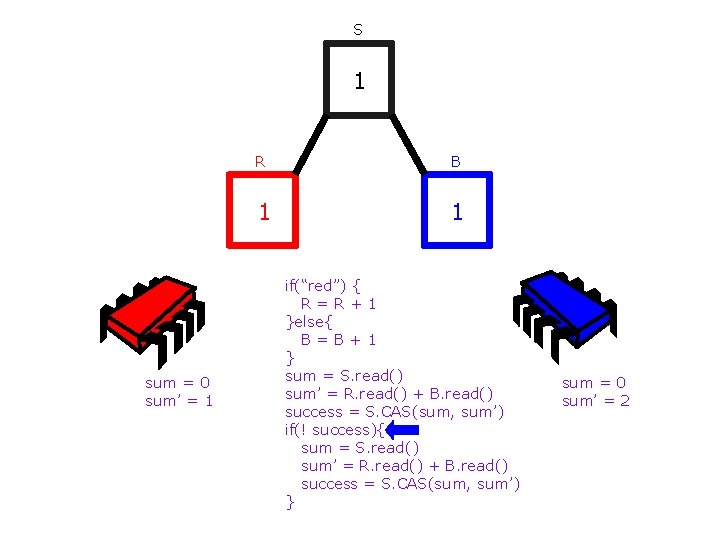
S 1 sum = 0 sum’ = 1 R B 1 1 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) if(! success){ sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) } sum = 1 sum’ = 2

S 1 sum = 0 sum’ = 1 R B 1 1 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) if(! success){ sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) } sum = 1 sum’ = 2

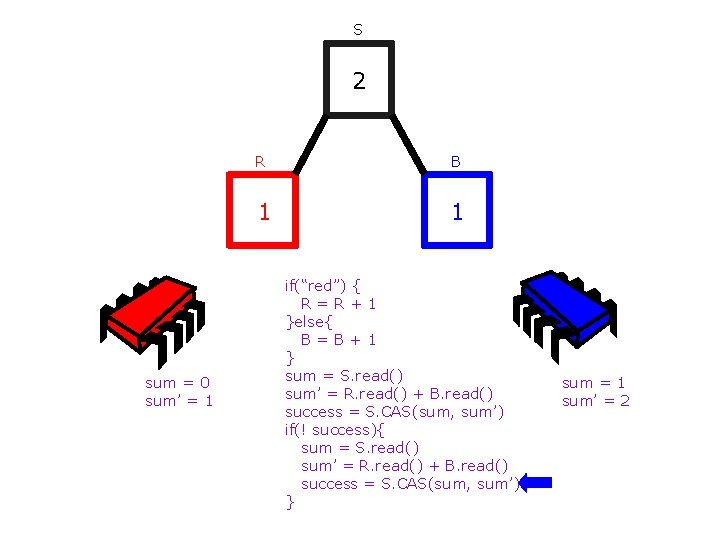
S 2 sum = 0 sum’ = 1 R B 1 1 if(“red”) { R=R+1 }else{ B=B+1 } sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) if(! success){ sum = S. read() sum’ = R. read() + B. read() success = S. CAS(sum, sum’) } sum = 1 sum’ = 2

Roadmap for Counting Set Construction Counter: increment(), read() FAI counter: fetch-and-inc(), read() Counting Set

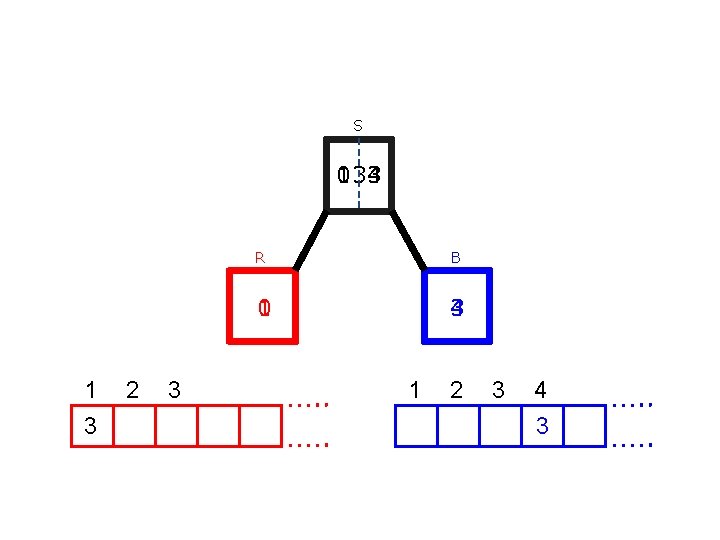
S 3 5 6 R B 0 1 3 4 5

S 034 1 3 2 3 R B 0 1 3 4 1 2 3 4 3

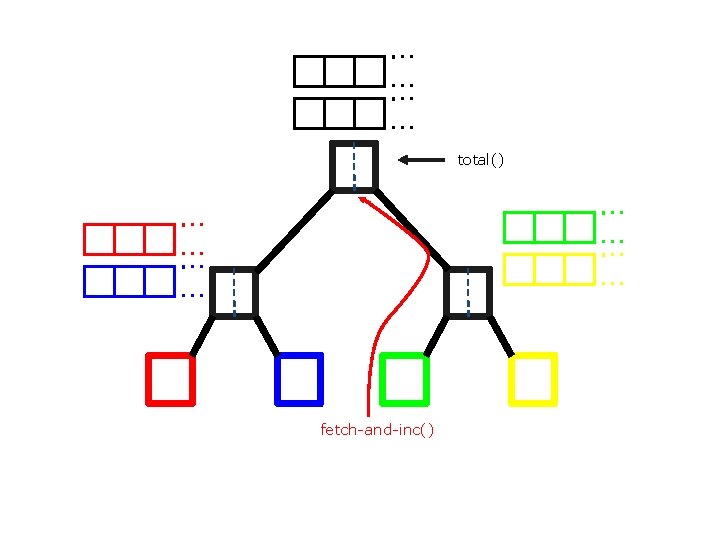
total() fetch-and-inc()
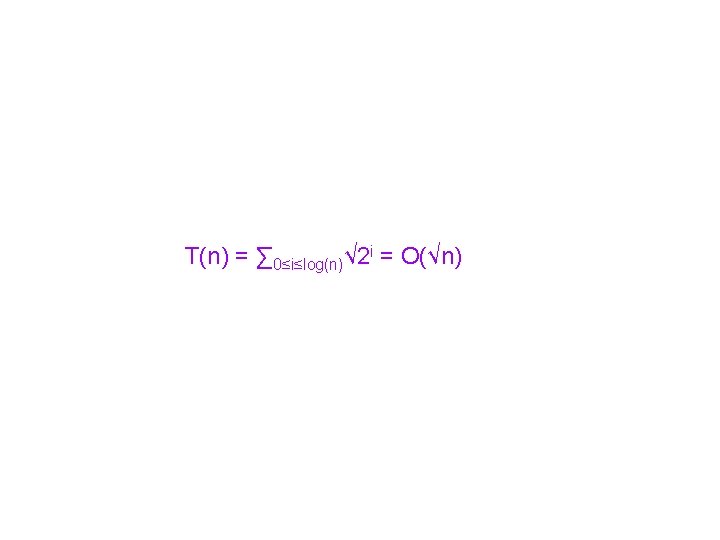

Roadmap for Counting Set Construction Counter: increment(), read() FAI counter: fetch-and-inc(), read() Counting Set

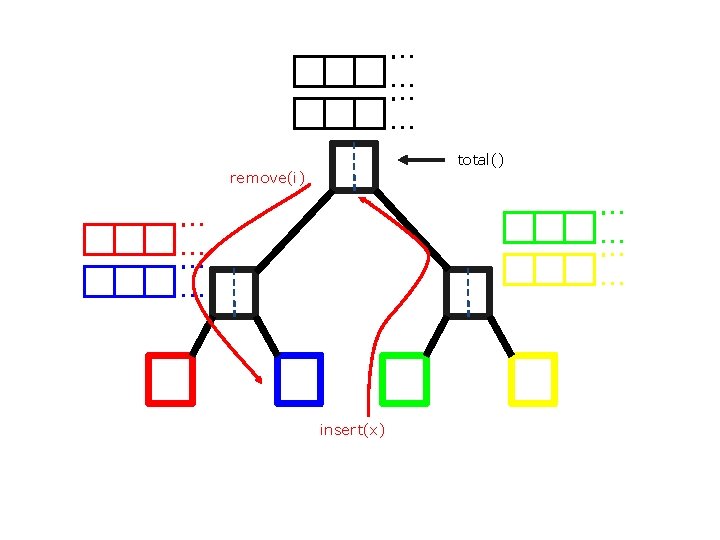
total() remove(i) insert(x)

Queue Design in Two Steps Queue for at most n pending enqueue operations (Counting Set) - O(√n) Queue for all the enqueue operations - O(1)

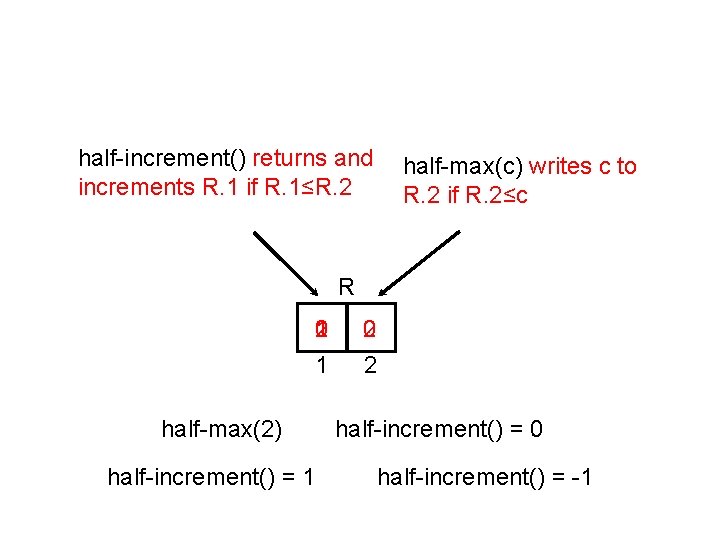
half-increment() returns and increments R. 1 if R. 1≤R. 2 half-max(c) writes c to R. 2 if R. 2≤c R 2 0 1 1 half-max(2) half-increment() = 1 2 0 2 half-increment() = 0 half-increment() = -1

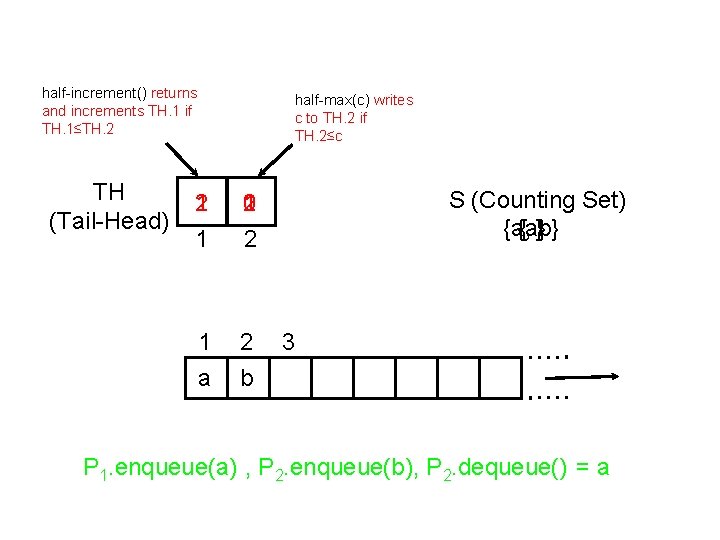
half-increment() returns and increments TH. 1 if TH. 1≤TH. 2 TH (Tail-Head) half-max(c) writes c to TH. 2 if TH. 2≤c 2 1 1 2 0 1 2 1 a 2 b S (Counting Set) {a} {a, { }b} 3 P 1. enqueue(a) , P 2. enqueue(b), P 2. dequeue() = a

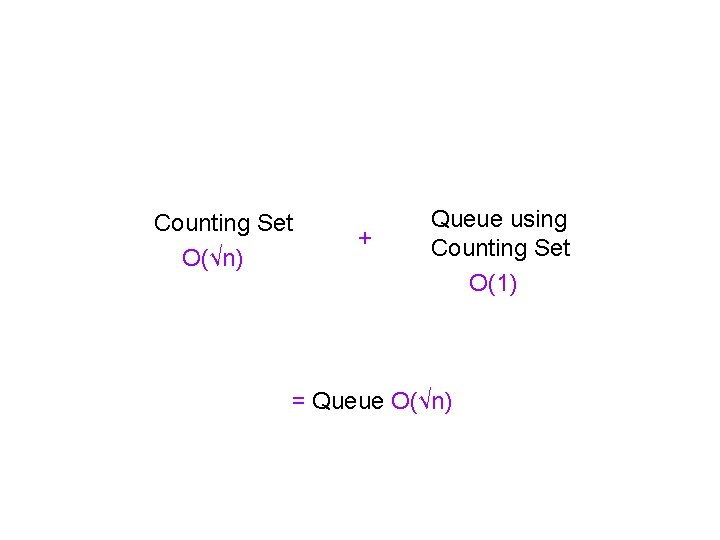
Counting Set O(√n) + Queue using Counting Set O(1) = Queue O(√n)

Counting Set seems quite generic to design other sublinear wait-free data structures. half-increment CAS FAA half-max

Thank You! Questions and Comments? kpankaj@ethz. ch