ON THE EFFICIENCY OF THE HAMMING CCENTERSTRING PROBLEMS

ON THE EFFICIENCY OF THE HAMMING C-CENTERSTRING PROBLEMS Amihood Amir Liam Roditty Jessica Ficler Oren Sar Shalom

Motivation – the Conference Location Problem

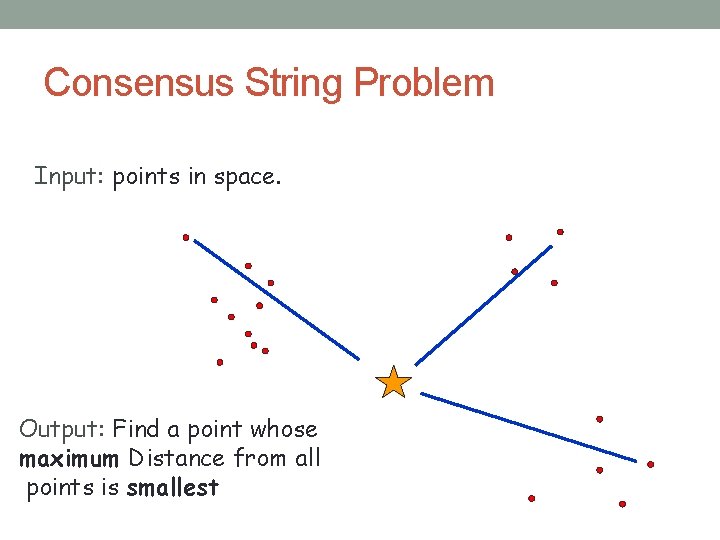
Consensus String Problem Input: points in space. Output: Find a point whose maximum Distance from all points is smallest

Hamming Distance •

Consensus String Problem (1 -HRC) •

History: Frances and Litman [1997]: Problem is NP-complete even for binary alphabets Therefore: 3 directions. 1. Solution for small k. 2. Fixed parameter tractability. 3. Approximation algorithms.

History: Solution for small k: Gramm, Niedermeier, and Rossmanith [2001] (3) Boucher, Brown, and Durocher [2008] (4 binary) A. , Landau, Na, Park, and Sim [2009] (3, radius & dist. sum optimization) A. , Paryenty, and Roditty [2012] (5 binary, l for all k: l k) 2

History: Fixed Parameter Tractability for all Parameters: Fixed l: Ben-Dor, Lancia, Perone, and Ravi [1997] Fixed k: Gramm, Niedermeier, and Rossmanith [2003] Fixed d: Sojanovic, Berman, Gumucio, Hardison, and Miller [1997] Lanctot, Li, Ma, Wang, and Zhang [1999] Sze, Lu, and Chen [2004]

History: Approximations: PTAS: Li, Ma, and Wang [2002] – not practical. Rounded LP: Ben-Dor, Lancia, Perone, and Ravi [1997] large number of variables: |Σ|l Chimani, Woste, and Bocker [2011]: can be reduced to: |Σ|(l-1) A. , Paryenty, and Roditty [2011]: |T(S)| |Σ| (T(S)= set of column types)

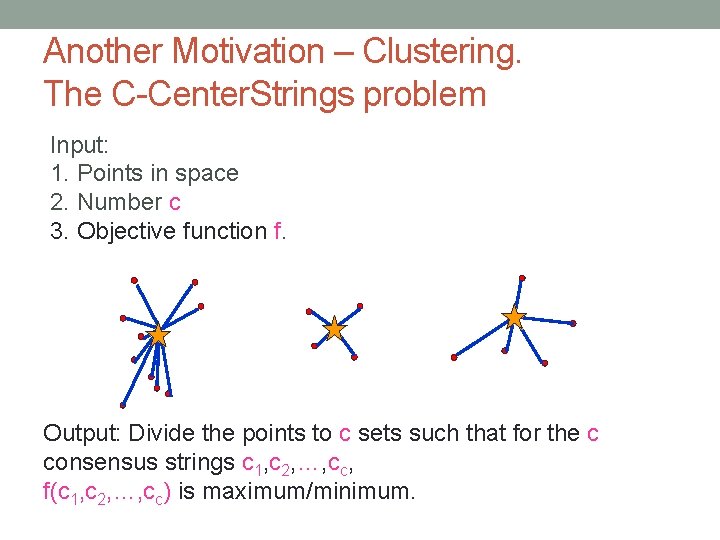
Another Motivation – Clustering. The C-Center. Strings problem Input: 1. Points in space 2. Number c 3. Objective function f. Output: Divide the points to c sets such that for the c consensus strings c 1, c 2, …, cc, f(c 1, c 2, …, cc) is maximum/minimum.

Three Types of Objective functions: • Let HRC (Hamming Radius Clustering) be the consensus string problem defined before. 1. c-HRC: partition into c sets, each of which has center with radius d. • 2. c-HRLC: partition into c sets, each of which has center with radius d, but center is part of input set. • 3. c-HRSC: partition into c sets, each of which has a center and the sum of the radii does not exceed d.

The Hamming radius c-clustering problem (c-HRC) Example: For the following strings and d=1, we show it belongs to 2 -HRC.

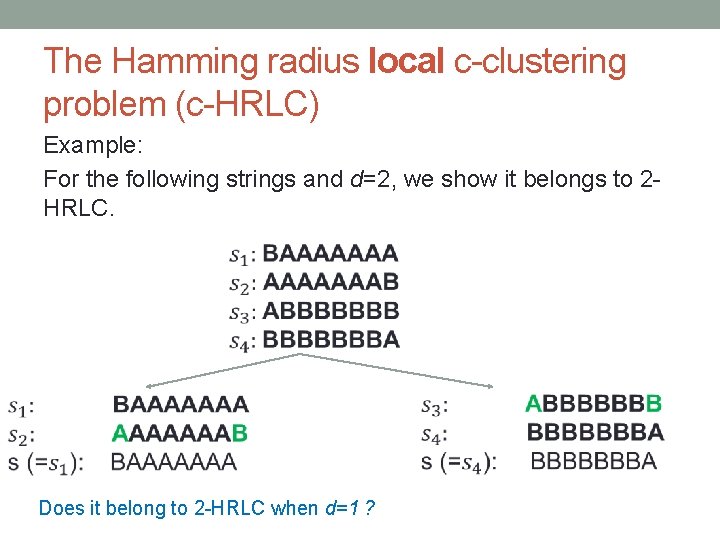
The Hamming radius local c-clustering problem (c-HRLC) Example: For the following strings and d=2, we show it belongs to 2 HRLC. Does it belong to 2 -HRLC when d=1 ?

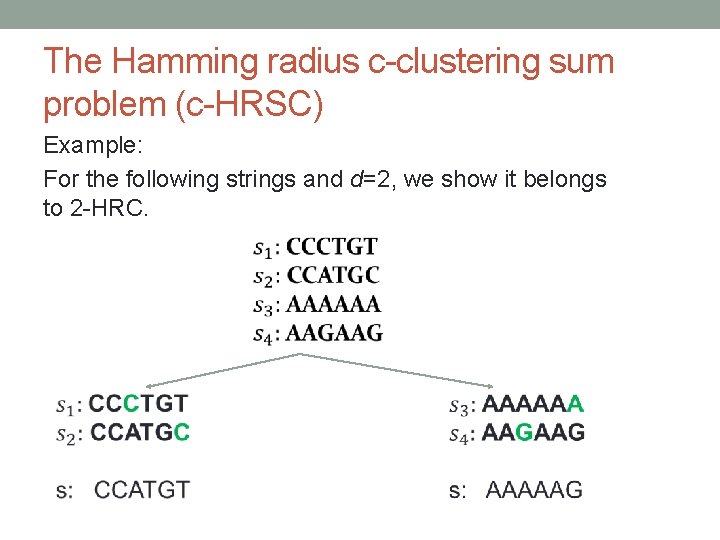
The Hamming radius c-clustering sum problem (c-HRSC) Example: For the following strings and d=2, we show it belongs to 2 -HRC.

In this Paper: We consider: 1. Parametetrized Complexity, and 2. Approximations Small k is not too meaningful in the context of clustering.

C-Center. String Parameterized Complexity c Fixed HRC HRLC HRSC k Fixed NPC polynomial time NPC polynomial time d Fixed (d=1) d/l and c Fixed l Fixed (l=2) NPC polynomial time ? ? polynomial time NPC ? polynomial time ?

Theorem: HRC, HRLC and HRSC can be solved in polynomial time for fixed k. • If k≤c then input strings can be assigned to c centers where d=0. • Otherwise c<k. There are ck<kk options for partitioning k strings to c sets. - For each set, find the consensus center in polynomial time. - The partition that gives the best result is the optimal solution.

C-Center. String Parameterized Complexity c Fixed HRC HRLC HRSC k Fixed NPC polynomial time NPC polynomial time d Fixed (d=1) d/l and c Fixed l Fixed (l=2) NPC polynomial time ? ? polynomial time NPC ? polynomial time ?

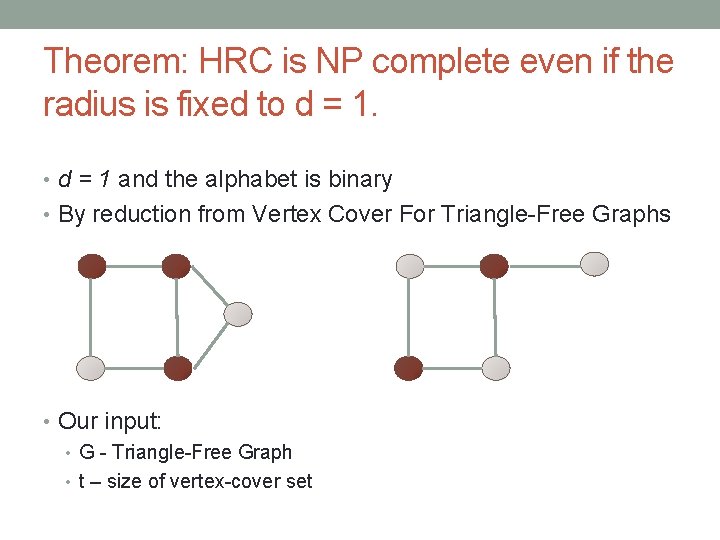
Theorem: HRC is NP complete even if the radius is fixed to d = 1. • d = 1 and the alphabet is binary • By reduction from Vertex Cover For Triangle-Free Graphs • Our input: • G - Triangle-Free Graph • t – size of vertex-cover set

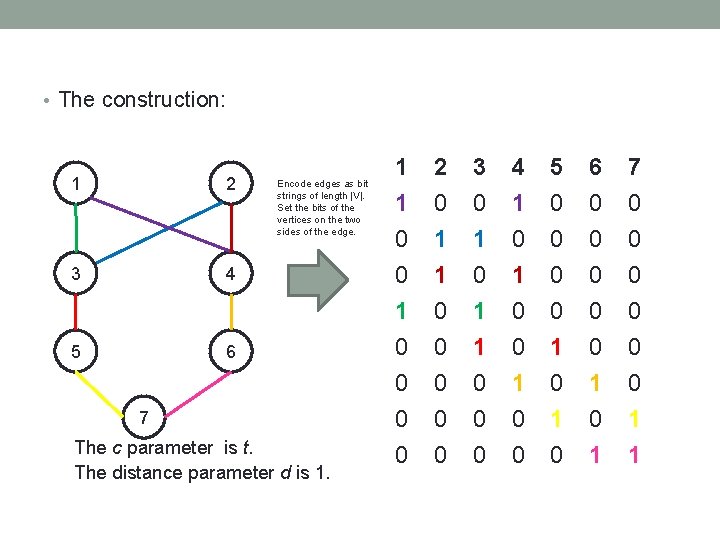
• The construction: 1 2 3 4 5 Encode edges as bit strings of length |V|. Set the bits of the vertices on the two sides of the edge. 6 7 The c parameter is t. The distance parameter d is 1. 1 1 0 0 2 0 1 1 3 0 1 0 4 1 0 1 5 0 0 0 6 0 0 0 7 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 1

• 1 2 3 4 5 6 7 0 1 1 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 1 1 0 0 0 1

• 0 1 1 0 0 0 0 1 0 0

• 0 0 1 0 1 0 0 0 0 ? ?

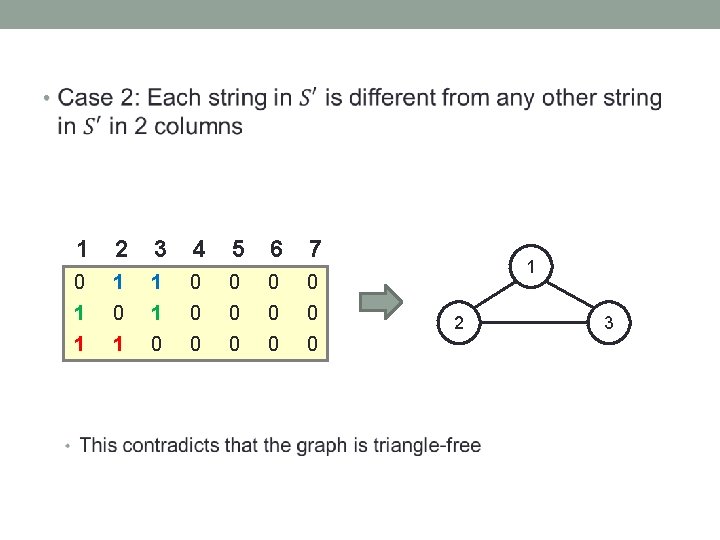
• 1 2 3 4 5 6 7 0 1 1 0 0 0 0 1 1 0 0 0 1 2 3

C-Center. String Parameterized Complexity c Fixed HRC HRLC HRSC k Fixed NPC polynomial time NPC polynomial time d Fixed (d=1) d/l and c Fixed l Fixed (l=2) NPC polynomial time ? ? polynomial time NPC ? polynomial time ?

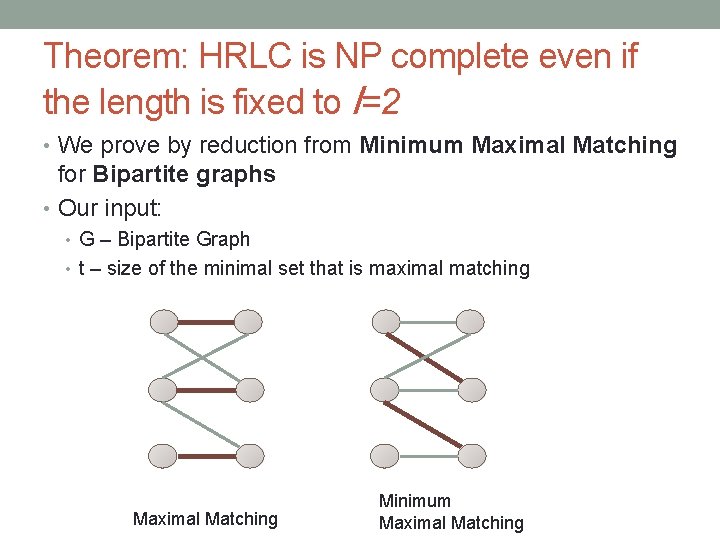
Theorem: HRLC is NP complete even if the length is fixed to l=2 • We prove by reduction from Minimum Maximal Matching for Bipartite graphs • Our input: • G – Bipartite Graph • t – size of the minimal set that is maximal matching Maximal Matching Minimum Maximal Matching

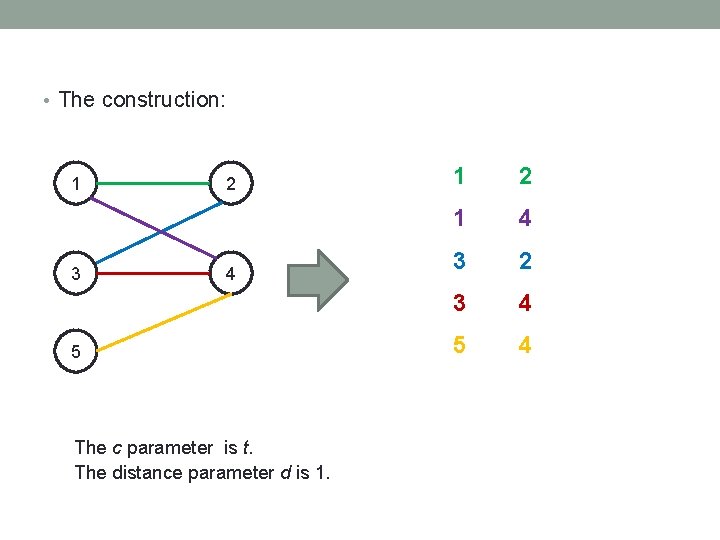
• The construction: 1 3 2 4 5 The c parameter is t. The distance parameter d is 1. 1 2 1 4 3 2 3 4 5 4

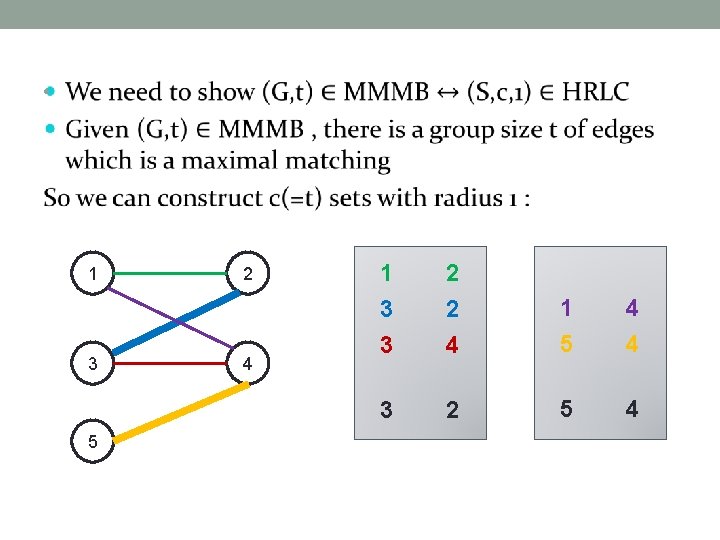
• 1 3 5 2 4 1 3 3 2 2 4 1 5 4 4 3 2 5 4

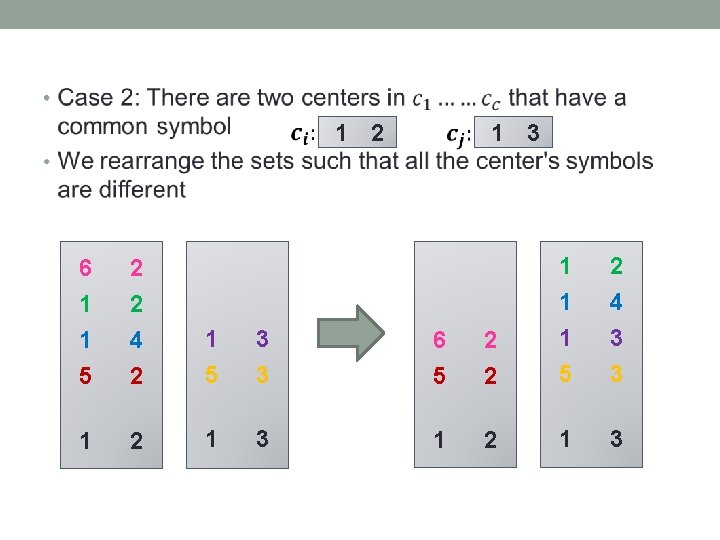
• 1 2 1 3 6 1 1 5 2 2 4 2 1 5 3 3 6 5 1 2 1 3 1 2 2 1 1 1 5 2 4 3 3 2 1 3

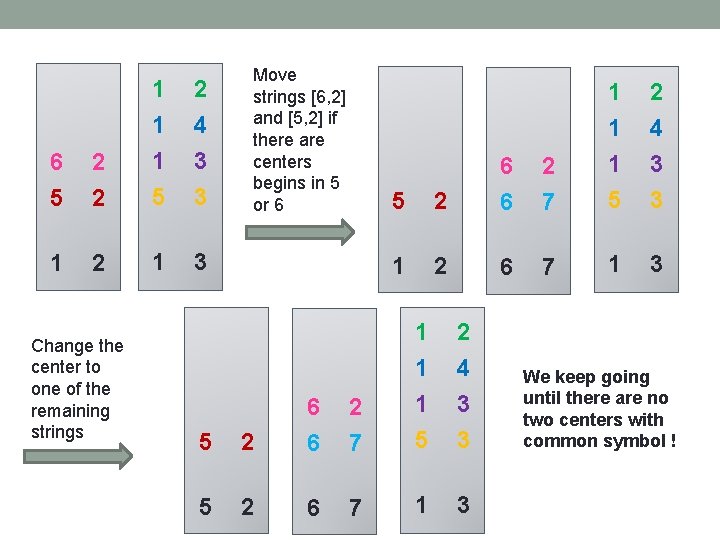
6 5 2 2 1 1 1 5 1 2 1 Change the center to one of the remaining strings 2 4 3 3 3 Move strings [6, 2] and [5, 2] if there are centers begins in 5 or 6 5 2 6 6 1 2 6 2 7 1 1 1 5 7 1 2 4 3 3 3 We keep going until there are no two centers with common symbol !

Approximation Algorithms • 1. A linear-time 4 -Approximation for the 2 -HRSC problem. • 2. A polynomial time 3 -Approximation for the 2 -HRSC problem. • 3. Special case PTAS – by computing the clusters and doing 1 -HRC approximation on each cluster.

Lemma • >2 d >2 d

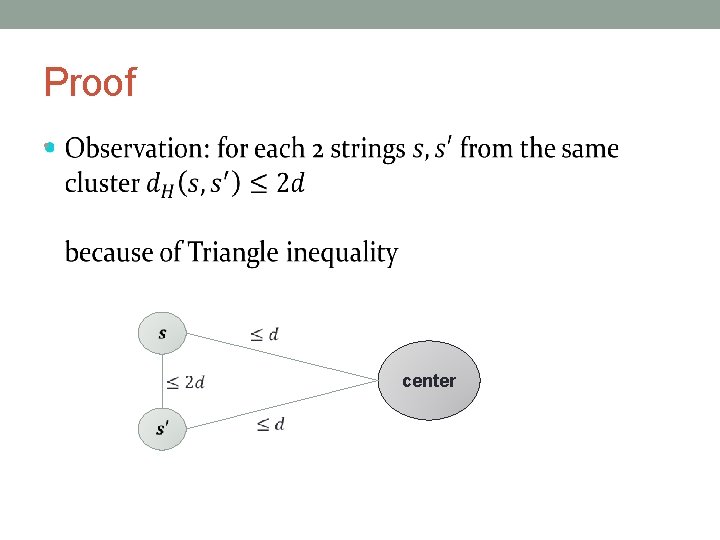
Proof • center

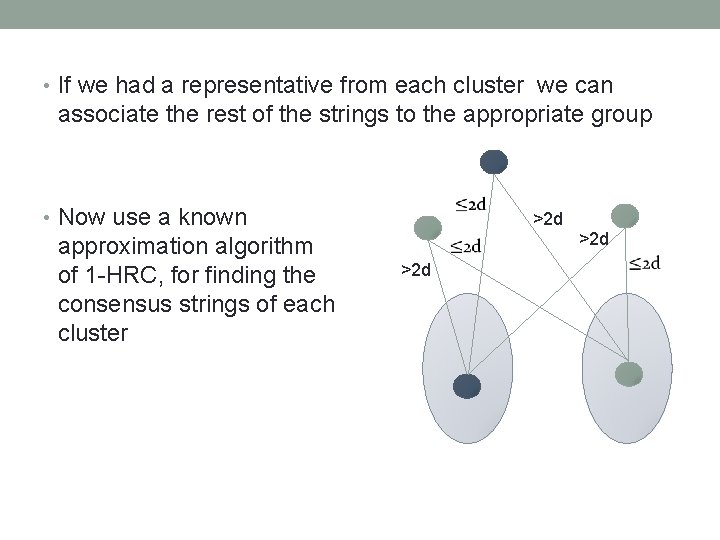
• If we had a representative from each cluster we can associate the rest of the strings to the appropriate group • Now use a known approximation algorithm of 1 -HRC, for finding the consensus strings of each cluster >2 d >2 d

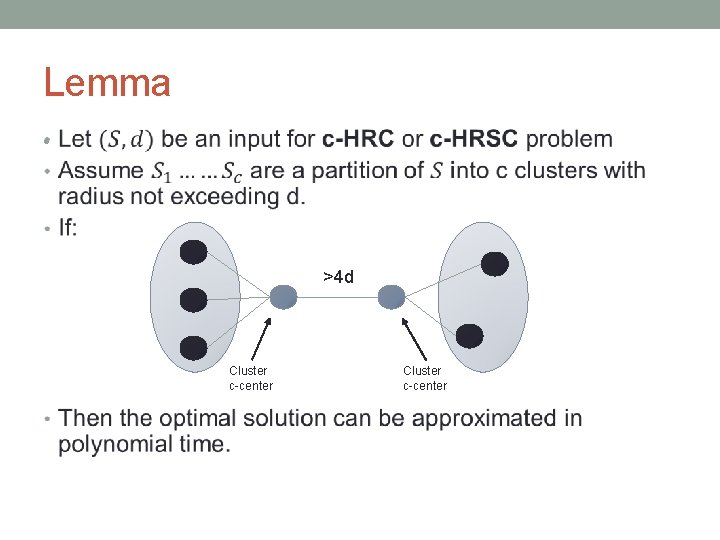
Lemma • >4 d Cluster c-center

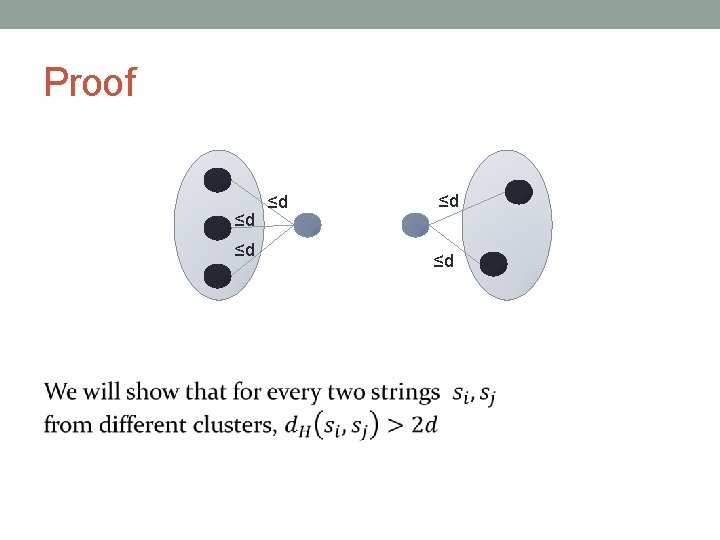
Proof ≤d ≤d ≤d

• 0 0 0 0 0 1 1 1 1 0 0 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 1 1 1 0 0 0

0 0 0 0 0 1 1 1 1 0 0 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 1 1 1 0 0 0 •

Polynomial time approximation algorithm for 2 -HRSC problem •

Future work 1. We presented a heuristic algorithm that did very well in practice – what is its approximation ratio? 2. There are some gaps in the parameterized complexity table: a. What happens in the HRLC/HRSC cases for fixed d? b. What happens in the HRC/HRSC cases for fixed l? 3. Is there a PTAS for c-HRC? 4. Can we approximate c-HRC using LP? SDP?