On the Characteristics of the Neutrino Events in

On the Characteristics of the Neutrino Events in (Ultra-)High Energy Astrophysics Experiments from the view point of Energy Estimation Akeo Misaki Research Institute For Science and engineering, Waseda University, Tokyo, Japan

Invitation to a point in dispute • The Fundamental parameters in (Ultra-)High Energy Astrophysics are: 1. Reliable Estimation of the Energies of the Neutrino Events 2. Reliable Estimation of the Incident Direction of the Neutrino Events To invite the participants to a point dispute, let us start from CONCLUSION, not INTRODUCTION.

Conclusion 1 1. Muon Neutrino Events: Inevitably Partially Contained Events One could not even estimate the energies of the muons from muon neutrino events (! ? ) 2. Electron Neutrino Events: Usually, Fully Contained Events. Inevitably, Partially Contained Events in Ultra-High Energies (LPM shower)

Conclusion 2 • COMPUTER NUMERICAL EXPERIMENTS • should be carried out simultaneously together with the REAL XPERIMENTS CONCERNED, not in the usual sense of Monte Carlo Simulation.

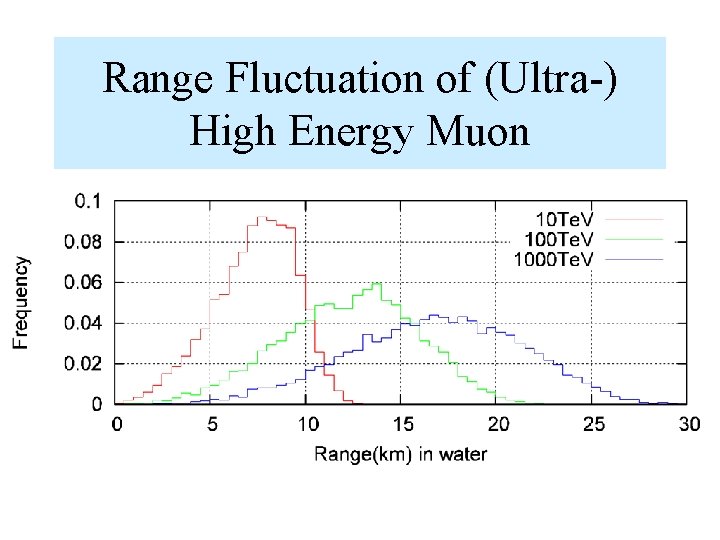
Range Fluctuation of (Ultra)-High Energy Muons • The Muon Range with Definite Energy is governed by the stochastic characters of the direct electron pair production, remsstrahlung and nuclear interaction which are also the origins of the accompanied electron showers.

Range Fluctuation of (Ultra-) High Energy Muon

The Image of (Ultra-)High Energy Muon • Muons from Muon Neutrino Events should be recognized as an aggregate of electron cascade showers with different starting points and different primary energies. • “Electron clouds” are twined around such the muon. • Namely, the muon could not be imaged as “Single or Naked Muon “

Is the Muon Itself the Dominant Source for the Cherenkov Light ? • For the question, it enough to examine the track lengths concerned, because the Cherenkov light production is proportional to the corresponding track length. • Ratio= track lengths of electrons from the accompanied showers/(track lengths of electrons from the accompanied showers + track length of the muon )

The transition curves for the integral of the track lengths from the muon as whole

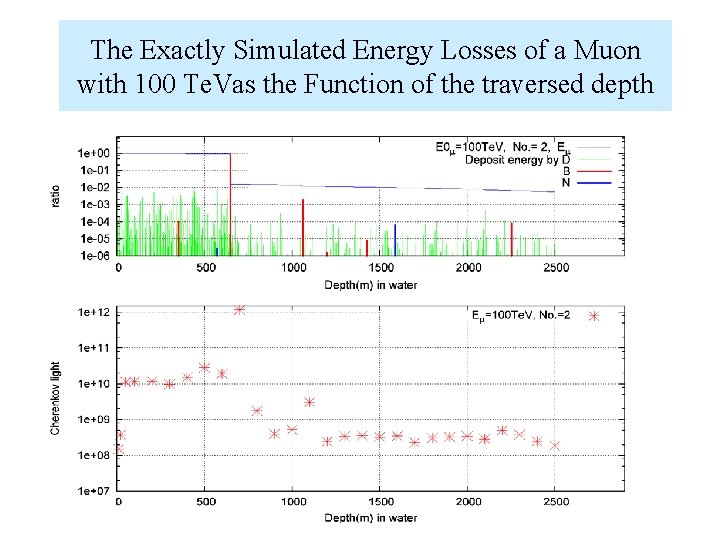
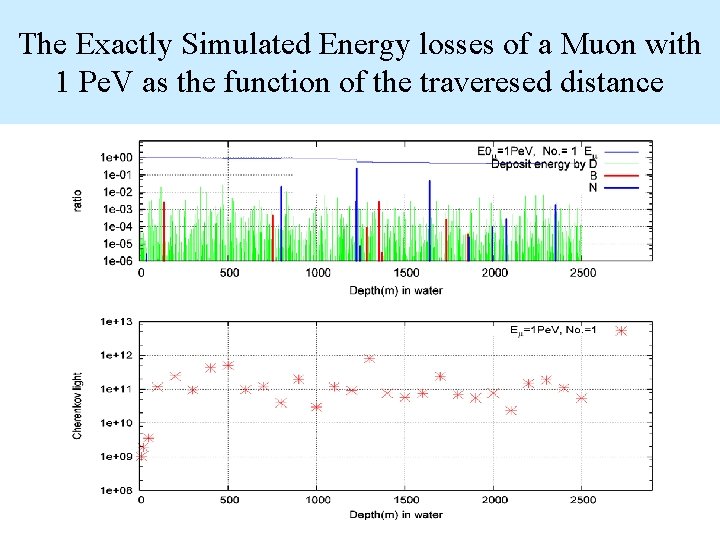
Cherenkov Light from the Mother Muon and Her Daughters Electron Shower • Accompanied electron showers are produced from the direct electron pair production, beremsstrahlung and nuclear interaction due to muon. • These electron showers are exactly simulated in one-dimensional treatment. • The electron segments in the simulated electron showers produced corresponding Cherenkov light

The Exactly Simulated Energy Losses of a Muon with 100 Te. Vas the Function of the traversed depth

The Exactly Simulated Energy losses of a Muon with 1 Pe. V as the function of the traveresed distance

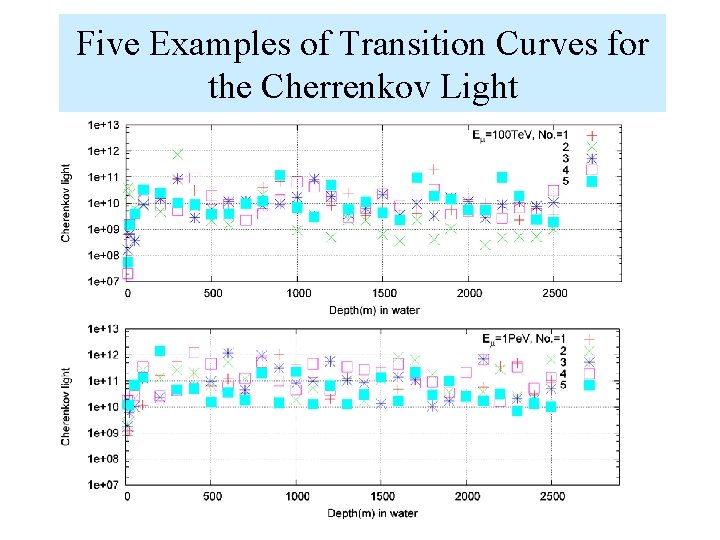
Five Examples of Transition Curves for the Cherrenkov Light

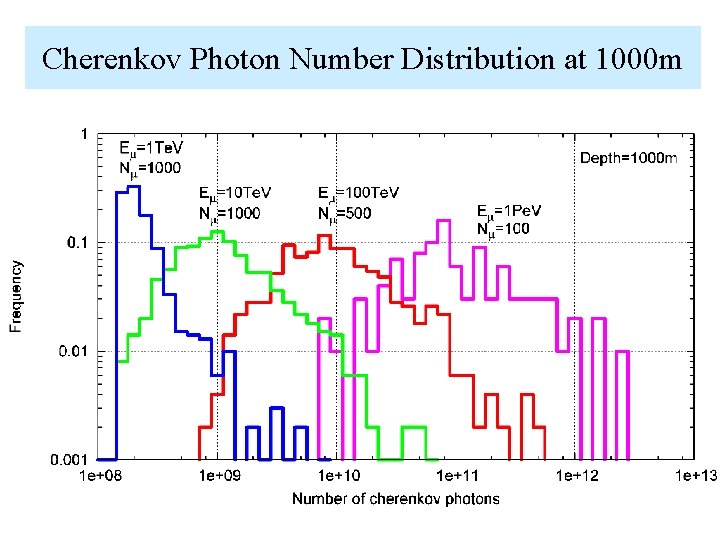
Cherenkov Photon Number Distribution at 1000 m

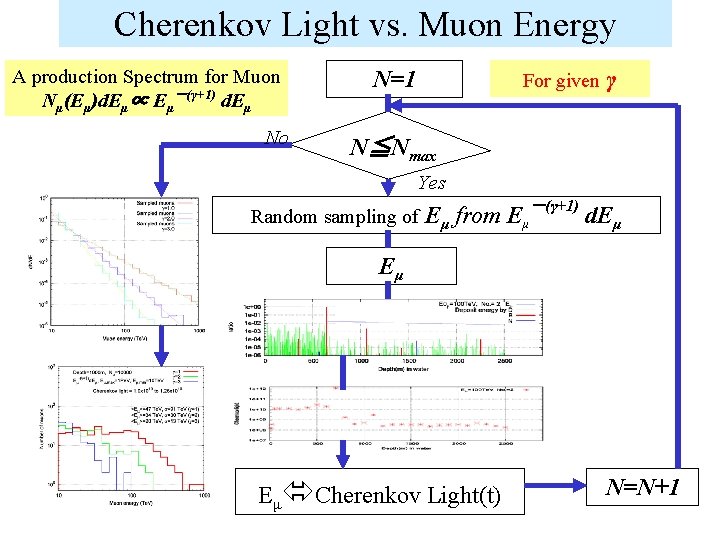
Cherenkov Light vs. Muon Energy A production Spectrum for Muon Nμ(Eμ)d. Eμ∝ Eμ－(γ+1) d. Eμ No N=1 For given γ N≦Nmax Yes Random sampling of Eμ from Eμ－(γ+1) d. Eμ Eμ Eμ Cherenkov Light(t) N=N+1

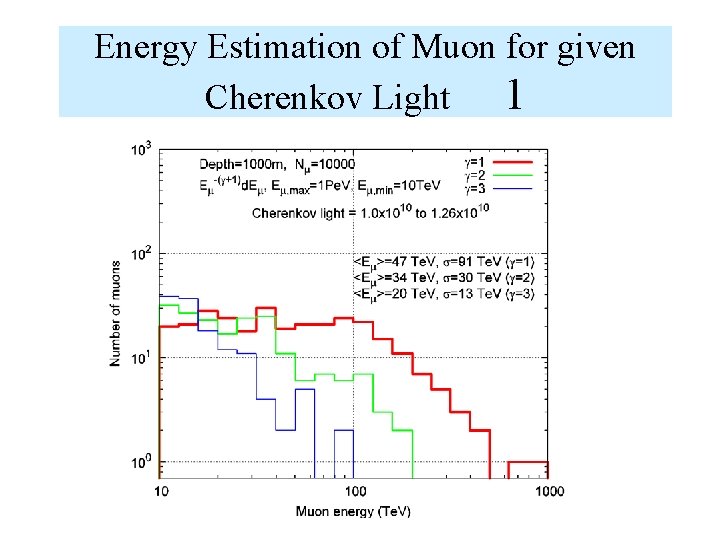
Energy Estimation of Muon for given Cherenkov Light　　1

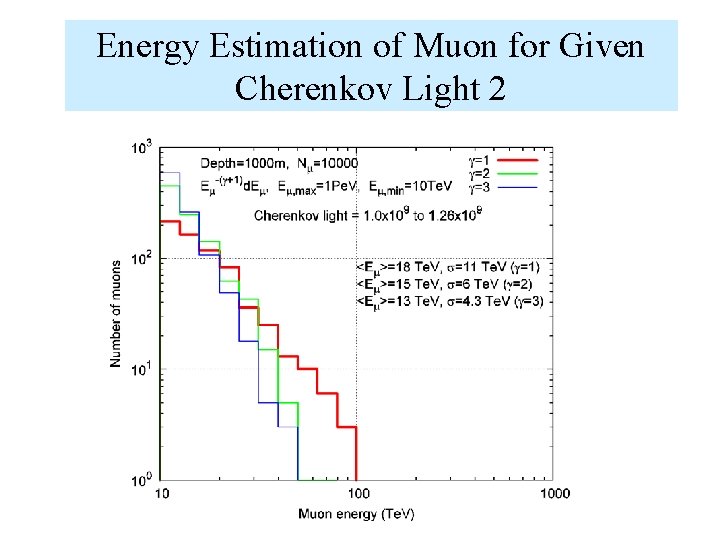
Energy Estimation of Muon for Given Cherenkov Light 2

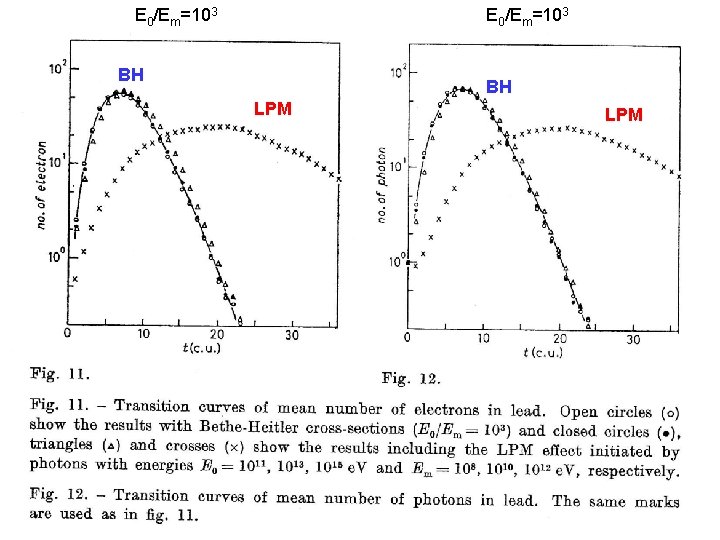
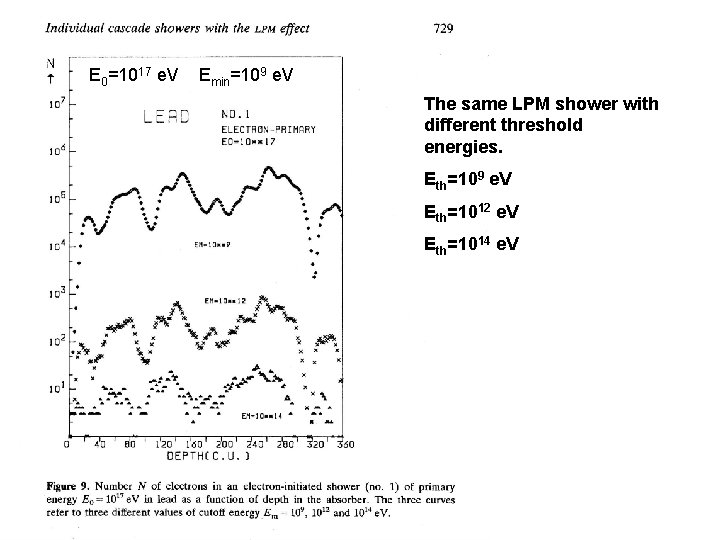
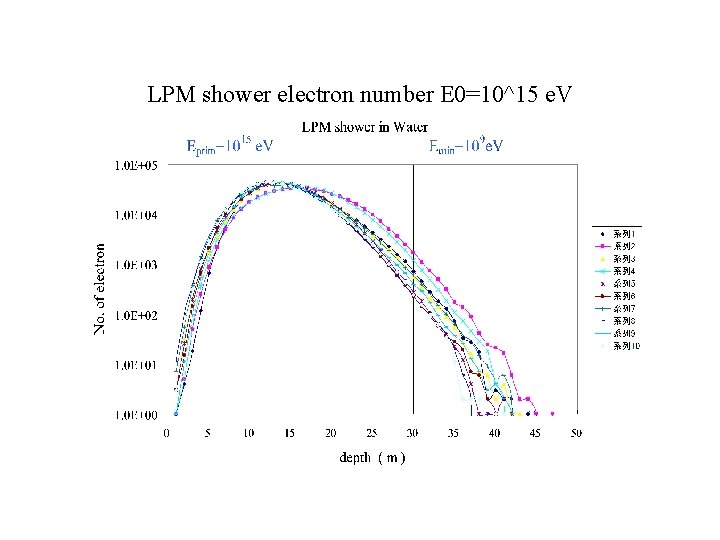
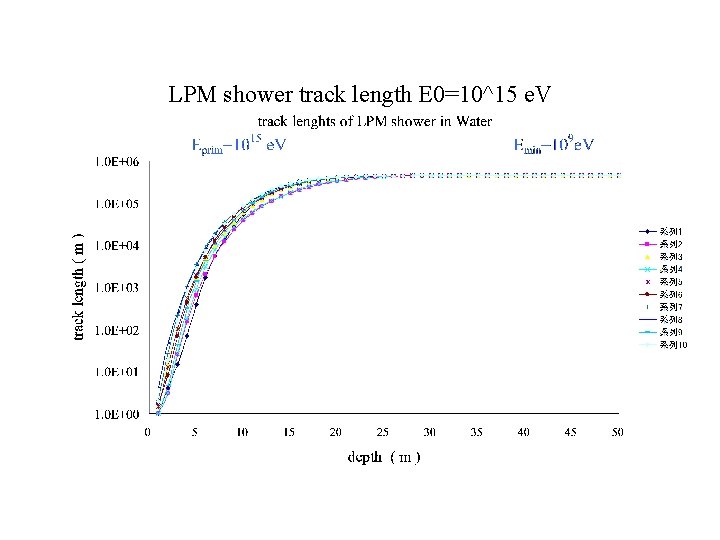
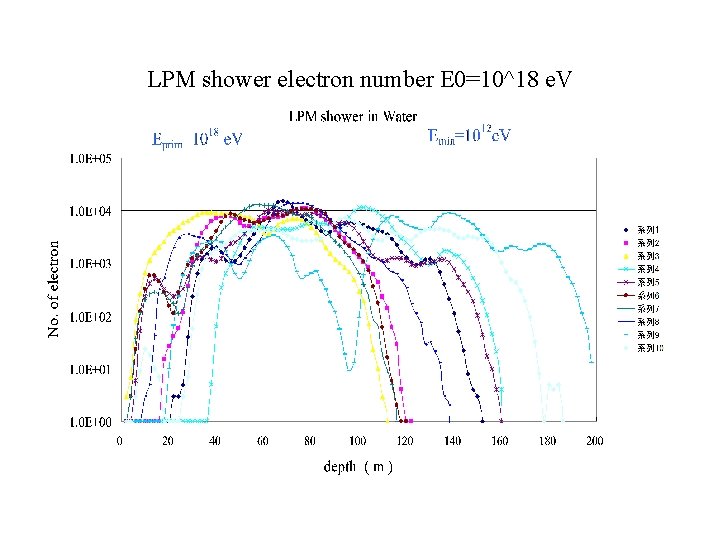
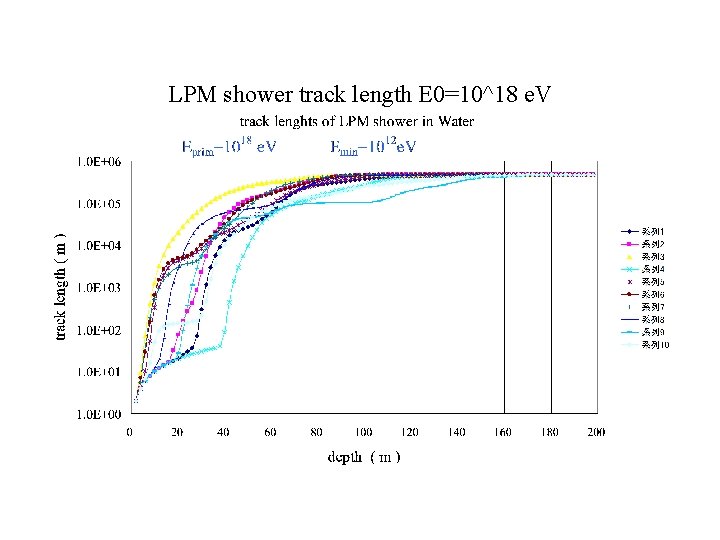
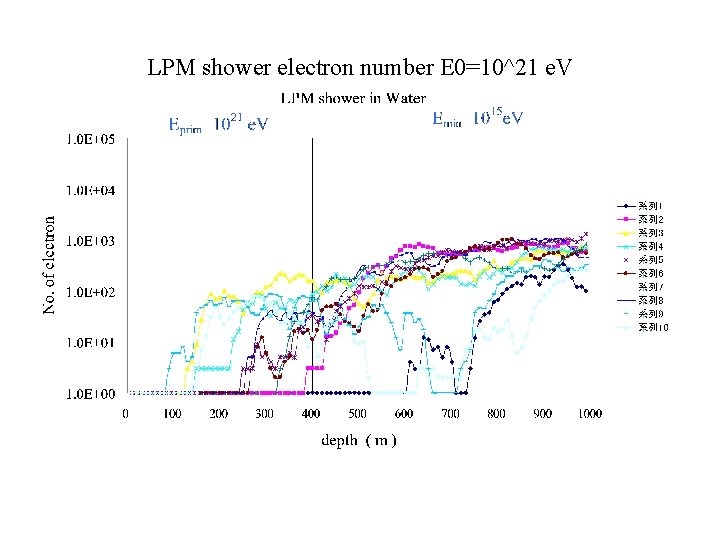
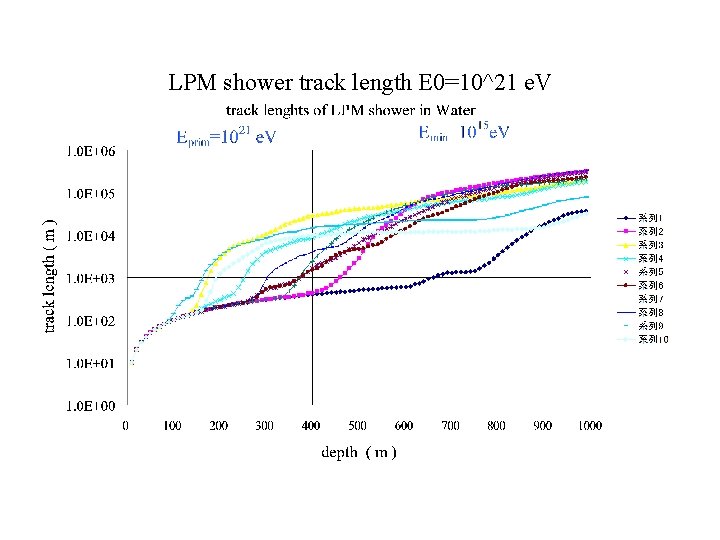
The LPM showers as Partially Contained Events • The Characteristics of the LPM showers: • [1] The Average behavior of the LPM showers is quite different from that of BH (Bethe-Heitler) Showers ( Konishi, Misaki and Fujimaki, Nuovo Cimento, (1978)) • [2] The. Individual Behavior of the LPM shower is quite different from that of the Averaged LPM shower ( Konishi, Adachi, Takahashi and Misaki, J. Phys. G, (1991)) •

The first prediction on the characteristics of the LPM shower Nuovo Cimento 48 A, 509 (1978)

E 0/Em=103 BH BH LPM

The first prediction on the multi-peak structure of the LPM shower.

E 0=1017 e. V Emin=109 e. V The same LPM shower with different threshold energies. Eth=109 e. V Eth=1012 e. V Eth=1014 e. V

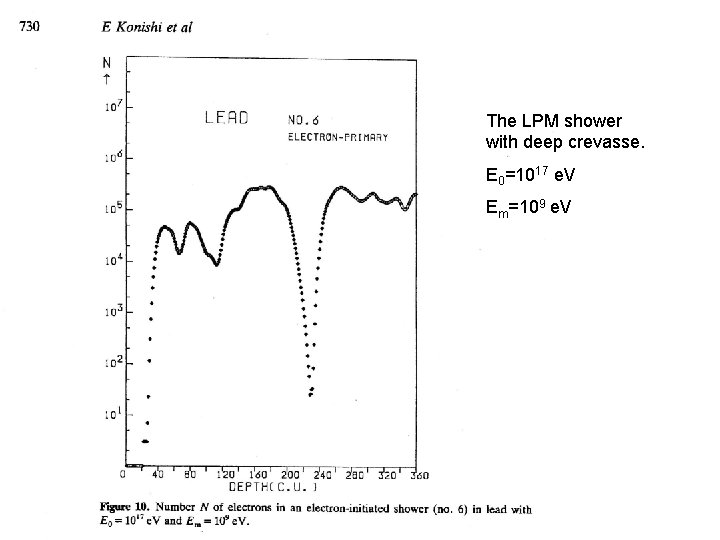
The LPM shower with deep crevasse. E 0=1017 e. V Em=109 e. V

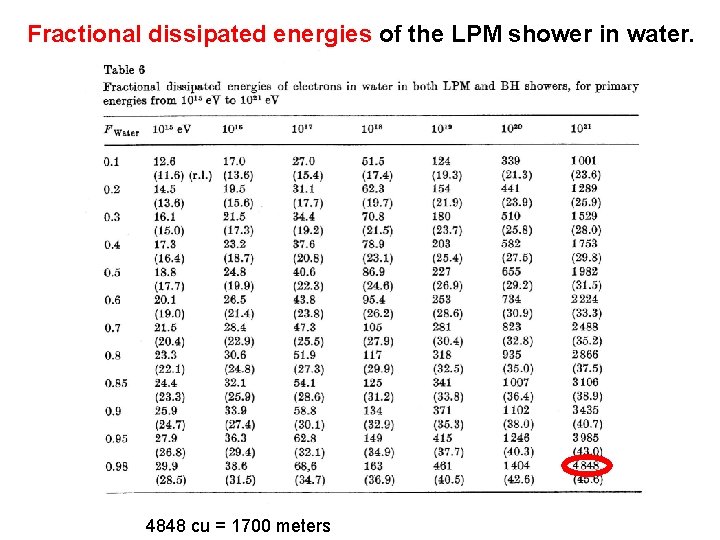
The first description on the average behavior of the LPM shower in water.

Fractional dissipated energies of the LPM shower in water. 4848 cu = 1700 meters

LPM shower electron number E 0=10^15 e. V

LPM shower track length E 0=10^15 e. V

LPM shower electron number E 0=10^18 e. V

LPM shower track length E 0=10^18 e. V

LPM shower electron number E 0=10^21 e. V

LPM shower track length E 0=10^21 e. V

Final Conclusion • At the early stage of the REAL XPERIMENTS, COMPUTER NUMRERICAL XPERIMENT should be being carried out with parallel them, collaborating with them closely. • In the presence of the Computer numerical experiment, one need not the transformation from the Cherenkov light to the Muon Energy