On the alternative approaches to ITRF formulation A





































- Slides: 82

On the alternative approaches to ITRF formulation. A theoretical comparison. Athanasios Dermanis Department of Geodesy and Surveying Aristotle University of Thessaloniki

The ITRF Formulation Problem Given: Time series of coordinates x. T(tk) & EOPS c. T(tk) from each space technique T Find: The optimal coordinate transformation parameters p. T(tk) (rotations, translation, scale) which transform the above time series x. T(tk), c. T(tk) into new ones x. ITRF(tk), c. ITRF(tk) best fitting the linear-in-time ITRF model for each network station i with constant initial coordinates x 0 i and velocities vi This procedure is called “stacking”

The ITRF Formulation Problem The basic stacking model: Coordinates: Earth Orientation Parameters (EOPs): Data from a set of 4 non-overlapping networks (VLBI, SLR, GPS, DORIS) connected through surveying observations between nearby stations at collocation sites

The ITRF Formulation Problem The basic stacking model: Coordinates: Earth Orientation Parameters (EOPs): ITRF parameters (initial coordinates, velocities, EOPs): Data from a set of 4 non-overlapping networks (VLBI, SLR, GPS, DORIS) connected through surveying observations between nearby stations at collocation sites

The ITRF Formulation Problem The basic stacking model: Coordinates: Earth Orientation Parameters (EOPs): Transformation parameters from the ITRF reference system to the reference system of each epoch within each technique: Data from a set of 4 non-overlapping networks (VLBI, SLR, GPS, DORIS) connected through surveying observations between nearby stations at collocation sites

The ITRF Formulation Problem The basic stacking model: Coordinates: Earth Orientation Parameters (EOPs): Observation noise - Assumed zero-mean and with known covariance cofactor matrices (single unknown reference variance 2): Data from a set of 4 non-overlapping networks (VLBI, SLR, GPS, DORIS) connected through surveying observations between nearby stations at collocation sites

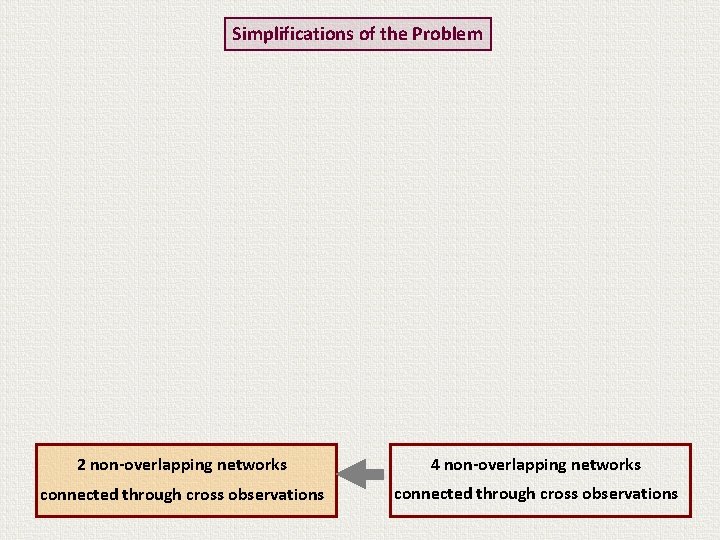
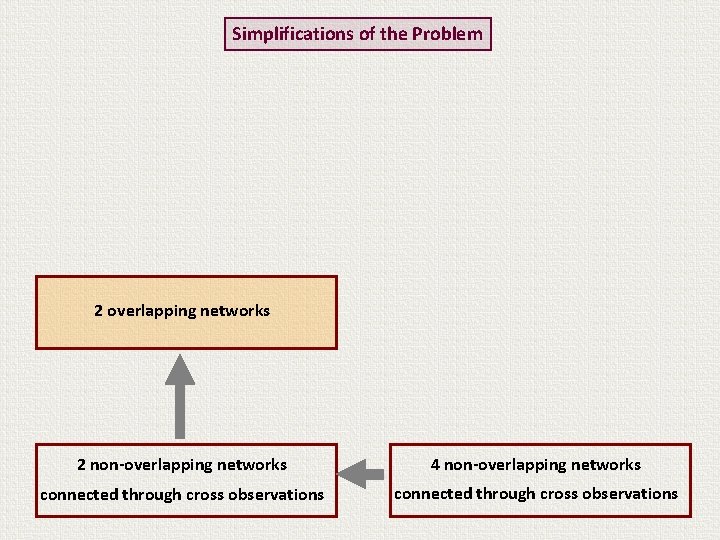
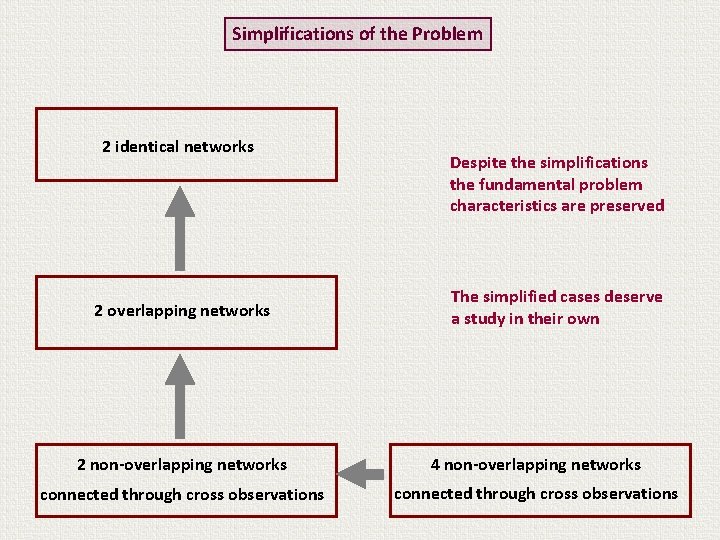
Simplifications of the Problem True ITRF formulation problem for VLBI, SLR, GPS, DORIS: 4 non-overlapping networks connected through cross observations

Simplifications of the Problem 2 non-overlapping networks 4 non-overlapping networks connected through cross observations

Simplifications of the Problem 2 overlapping networks 2 non-overlapping networks 4 non-overlapping networks connected through cross observations

Simplifications of the Problem 2 identical networks 2 overlapping networks 2 non-overlapping networks 4 non-overlapping networks connected through cross observations

Simplifications of the Problem 2 identical networks 2 overlapping networks Despite the simplifications the fundamental problem characteristics are preserved The simplified cases deserve a study in their own 2 non-overlapping networks 4 non-overlapping networks connected through cross observations

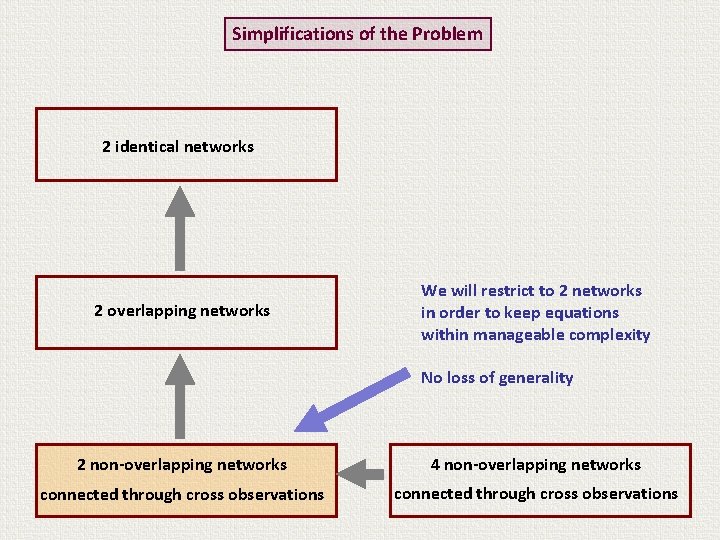
Simplifications of the Problem 2 identical networks 2 overlapping networks We will restrict to 2 networks in order to keep equations within manageable complexity No loss of generality 2 non-overlapping networks 4 non-overlapping networks connected through cross observations

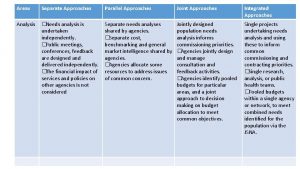
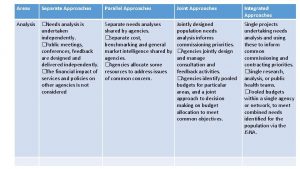
The two alternative approaches ONE STEP APPROACH Simultaneous adjustment of data from all techniques for the estimation of the ITRF parameters (multi-technique approach – simultaneous stacking) TWO STEP APPROACH (1) Adjustment of data from each technique separately for the estimation of per technique ITRF parameters (stacking per technique) (2) Combination of the ITRF estimates from each technique into final ITRF estimates

The two alternative approaches ONE STEP APPROACH – EQUIVALENT TWO-STEP FORMULATION (1) Separate solutions (2) Combination of separate solutions with addition of normal equations Final parameter estimates as weighted mean of separate estimates TWO STEP APPROACH (1) Adjustment of data from each technique separately for the estimation of per technique ITRF parameters (stacking per technique) (2) Combination of the ITRF estimates from each technique into final ITRF estimates

The two alternative approaches ONE STEP APPROACH – EQUIVALENT TWO-STEP FORMULATION (1) Separate solutions same (2) Combination of separate solutions with addition of normal equations Final parameter estimates as weighted mean of separate estimates TWO STEP APPROACH (1) Adjustment of data from each technique separately for the estimation of per technique ITRF parameters (stacking per technique) (2) Combination of the ITRF estimates from each technique into final ITRF estimates

The two alternative approaches ONE STEP APPROACH – EQUIVALENT TWO-STEP FORMULATION (1) Separate solutions (2) Combination of separate solutions with addition of normal equations Final parameter estimates as weighted mean of separate estimates Difference only in second steps TWO STEP APPROACH (1) Adjustment of data from each technique separately for the estimation of per technique ITRF parameters (stacking per technique) (2) Combination of the ITRF estimates from each technique into final ITRF estimates

The two alternative approaches ONE STEP APPROACH – EQUIVALENT TWO-STEP FORMULATION (1) Separate solutions (2) Combination of separate solutions with addition of normal equations Final parameter estimates as weighted mean of separate estimates TWO STEP APPROACH (1) Adjustment of data from each technique separately for the estimation of per technique ITRF parameters (stacking per technique) (2) Combination of the ITRF estimates from each technique into final ITRF estimates Separate solutions produce singular covariance matrices !

Models with rank defect due to lack of reference system definition

Models with rank defect due to lack of reference system definition Variation of parameters under change of reference system p = transformation parameters (rotations, displacement, scale)

Models with rank defect due to lack of reference system definition Variation of parameters under change of reference system p = transformation parameters (rotations, displacement, scale) Invariance of observables y = Ax and estimable parameters (functions of y)

Models with rank defect due to lack of reference system definition Variation of parameters under change of reference system p = transformation parameters (rotations, displacement, scale) Invariance of observables y = Ax and estimable parameters (functions of y) (total) inner constraints for reference system choice (usually partial inner constraints or other minimal constraints are employed)

Two identical networks This case does not apply to the ITRF formulation problem but has an interest of its own for other network applications

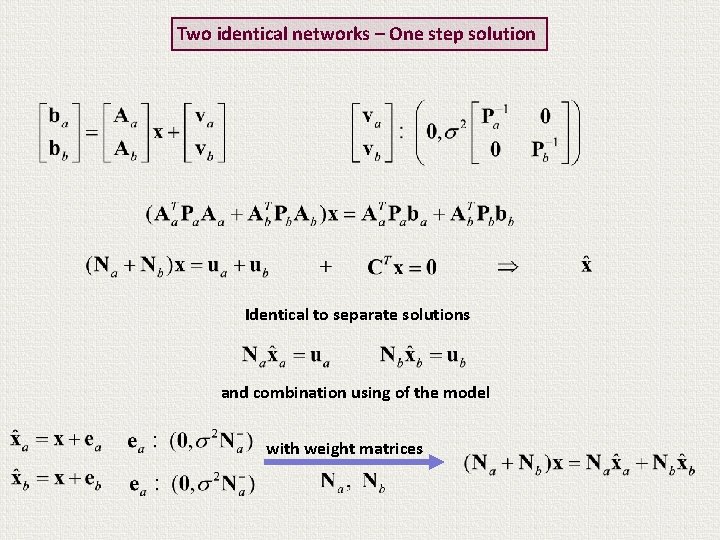
Two identical networks – One step solution Identical to separate solutions and combination using of the model with weight matrices

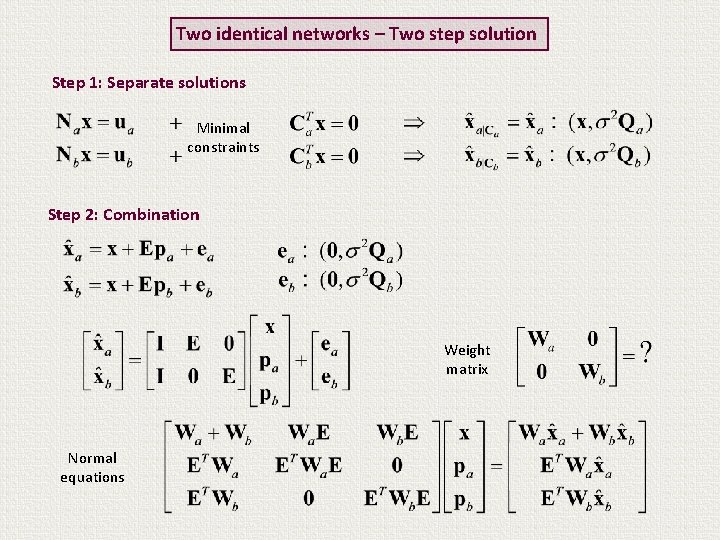
Two identical networks – Two step solution Step 1: Separate solutions Minimal constraints Step 2: Combination Weight matrix Normal equations

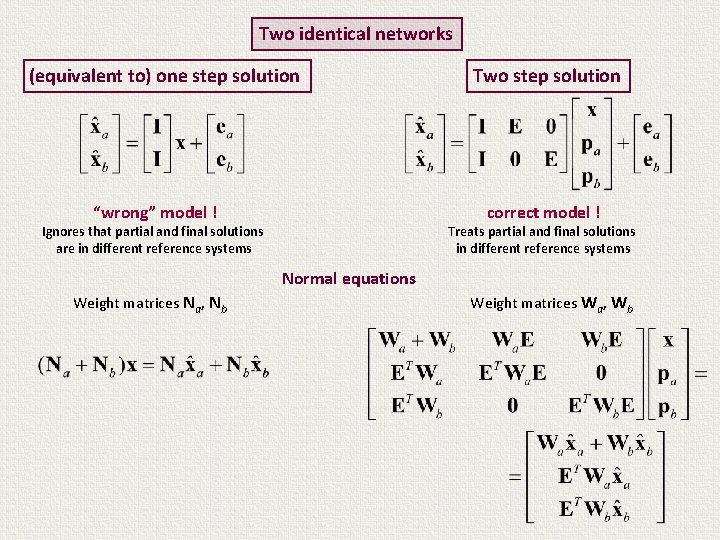
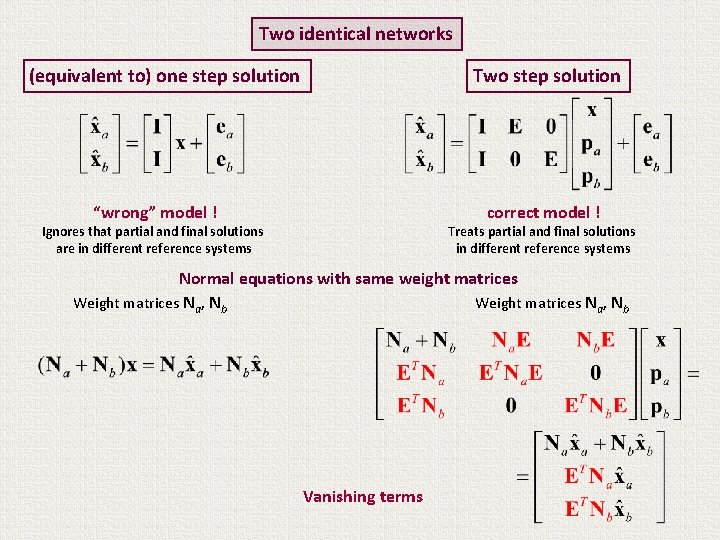
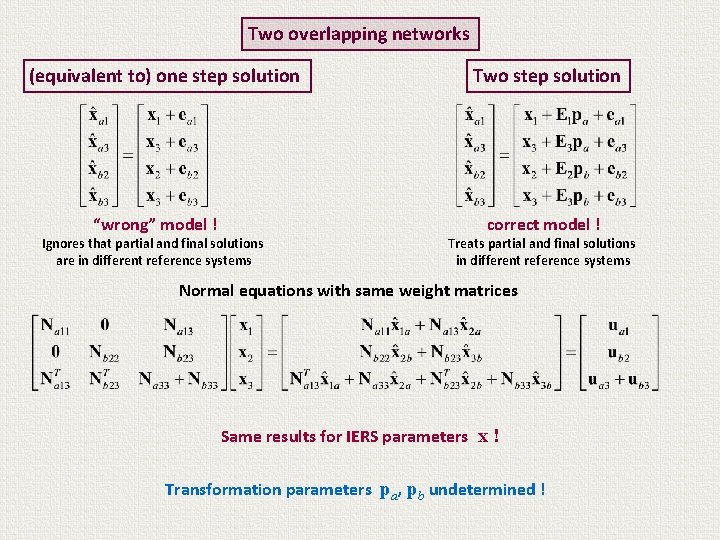
Two identical networks (equivalent to) one step solution “wrong” model ! Two step solution correct model ! Ignores that partial and final solutions are in different reference systems Treats partial and final solutions in different reference systems Normal equations Weight matrices Na, Nb Weight matrices Wa, Wb

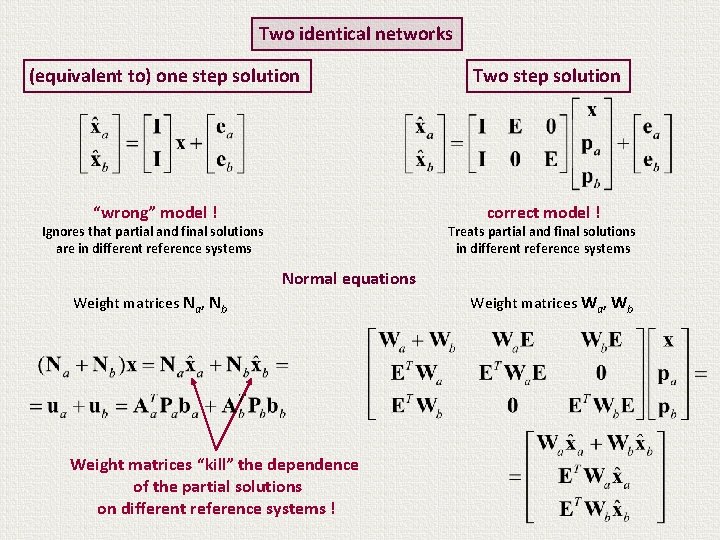
Two identical networks (equivalent to) one step solution “wrong” model ! Two step solution correct model ! Ignores that partial and final solutions are in different reference systems Treats partial and final solutions in different reference systems Normal equations Weight matrices Na, Nb Weight matrices “kill” the dependence of the partial solutions on different reference systems ! Weight matrices Wa, Wb

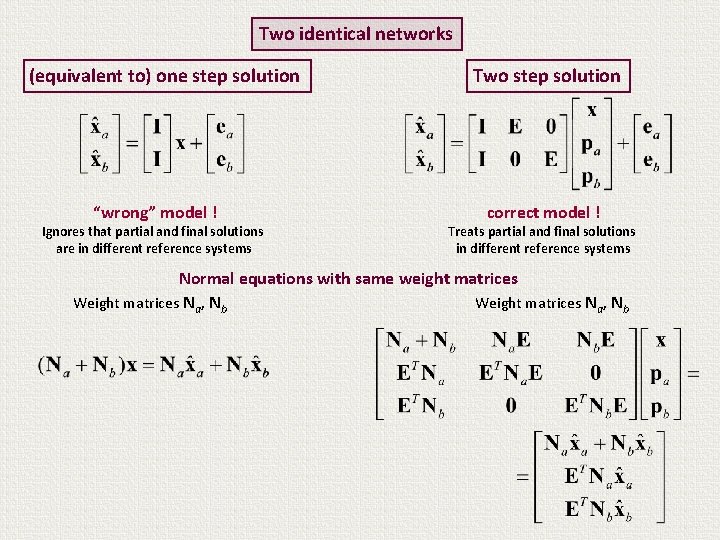
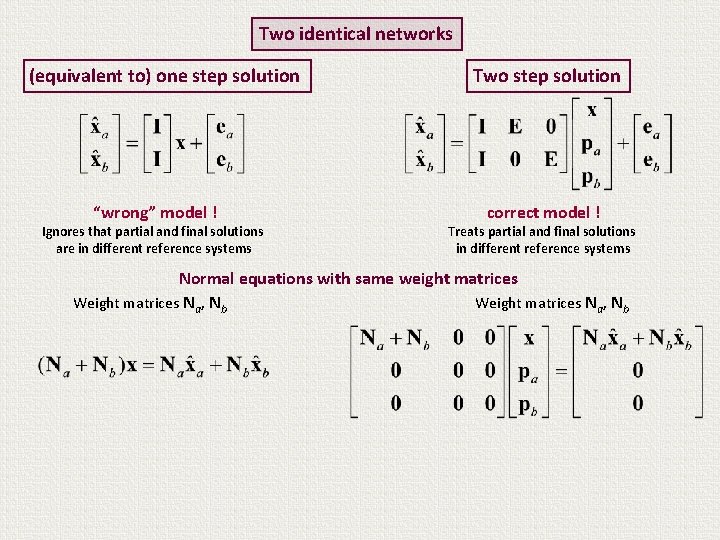
Two identical networks (equivalent to) one step solution “wrong” model ! Ignores that partial and final solutions are in different reference systems Two step solution correct model ! Treats partial and final solutions in different reference systems Normal equations with same weight matrices Weight matrices Na, Nb

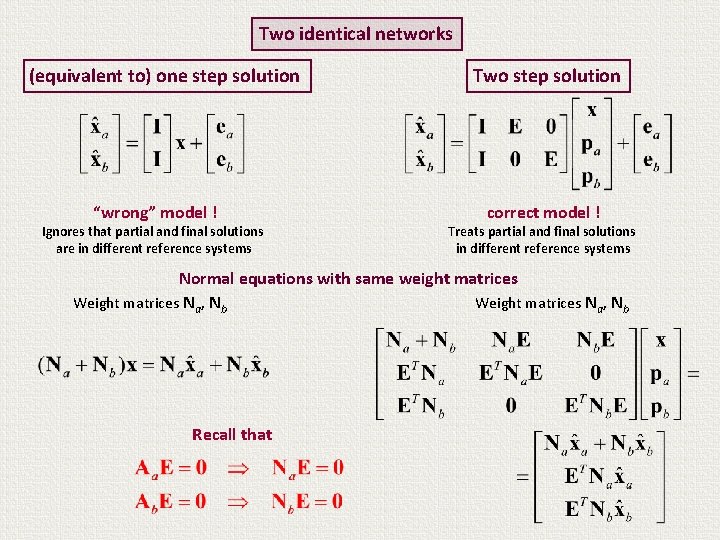
Two identical networks (equivalent to) one step solution “wrong” model ! Ignores that partial and final solutions are in different reference systems Two step solution correct model ! Treats partial and final solutions in different reference systems Normal equations with same weight matrices Weight matrices Na, Nb Recall that

Two identical networks (equivalent to) one step solution Two step solution “wrong” model ! correct model ! Ignores that partial and final solutions are in different reference systems Treats partial and final solutions in different reference systems Normal equations with same weight matrices Weight matrices Na, Nb Vanishing terms

Two identical networks (equivalent to) one step solution “wrong” model ! Ignores that partial and final solutions are in different reference systems Two step solution correct model ! Treats partial and final solutions in different reference systems Normal equations with same weight matrices Weight matrices Na, Nb

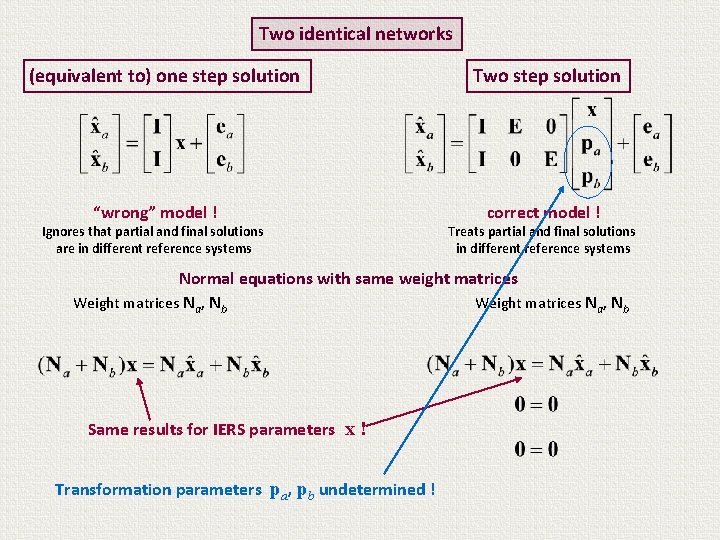
Two identical networks (equivalent to) one step solution “wrong” model ! Ignores that partial and final solutions are in different reference systems Two step solution correct model ! Treats partial and final solutions in different reference systems Normal equations with same weight matrices Weight matrices Na, Nb Same results for IERS parameters x ! Transformation parameters pa, pb undetermined !

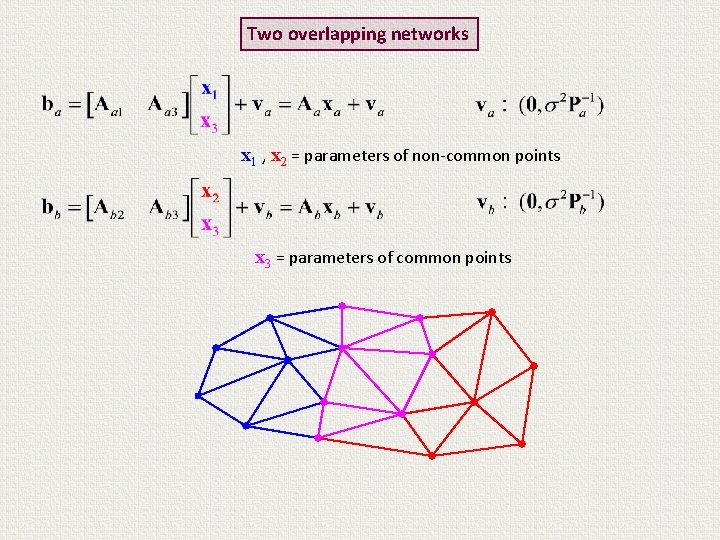
Two overlapping networks This case would apply to the ITRF formulation problem if perfect connections were available at collocation sites

Two overlapping networks x 1 , x 2 = parameters of non-common points x 3 = parameters of common points

Two overlapping networks – Separate solutions Network (a) solution: normal equations Network (b) solution: normal equations

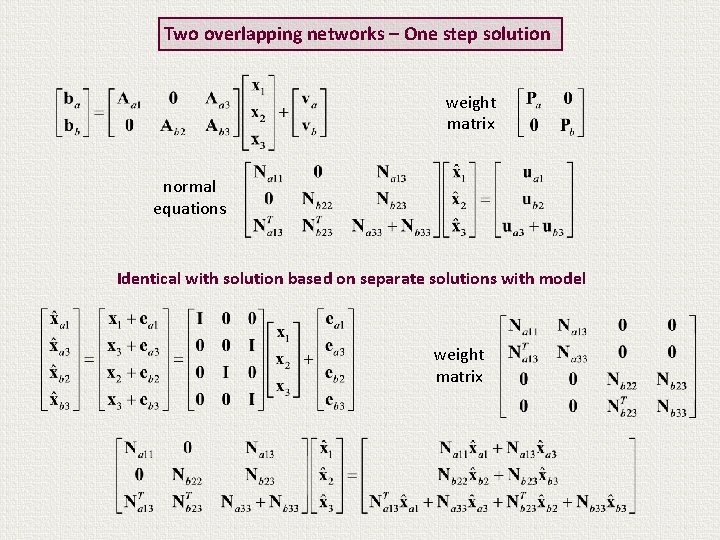
Two overlapping networks – One step solution weight matrix normal equations Identical with solution based on separate solutions with model weight matrix

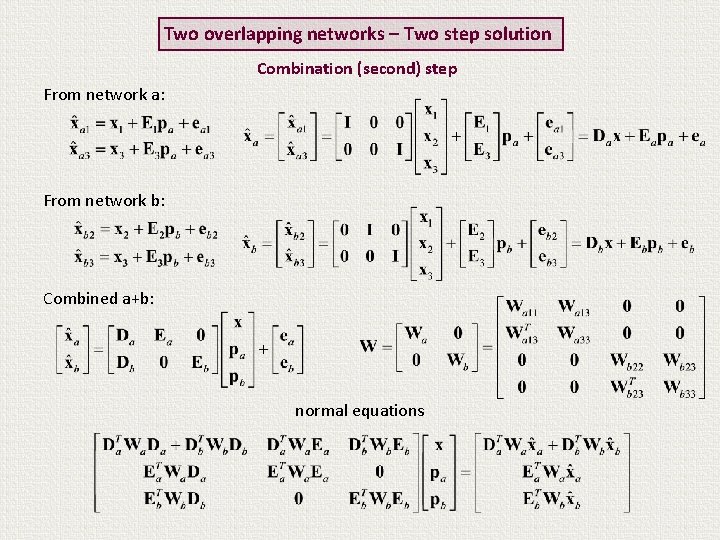
Two overlapping networks – Two step solution Combination (second) step From network a: From network b: Combined a+b: normal equations

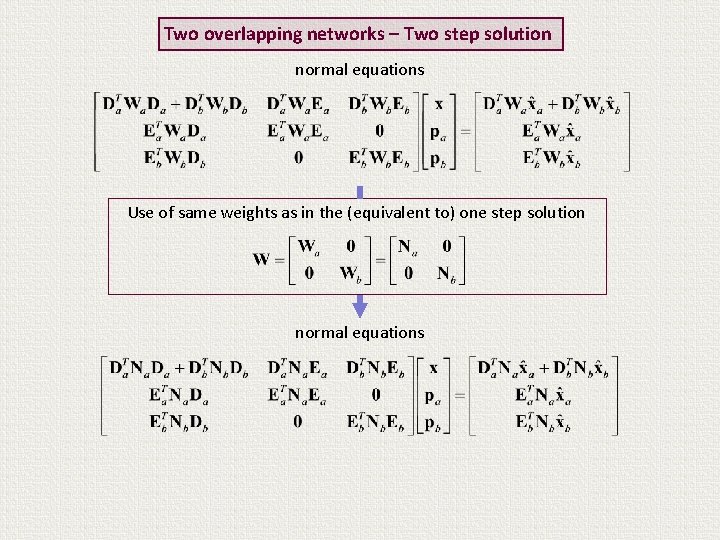
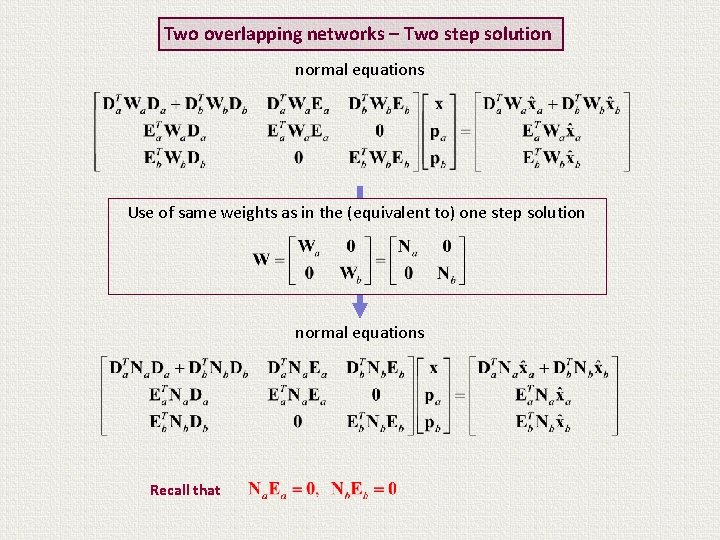
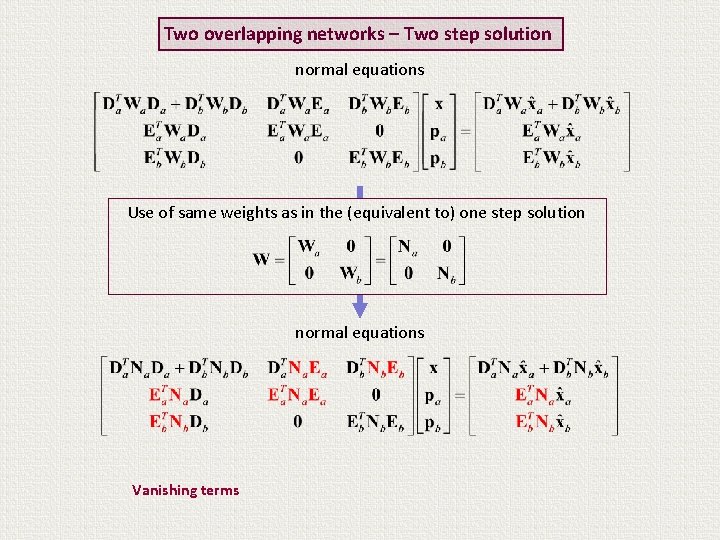
Two overlapping networks – Two step solution normal equations Use of same weights as in the (equivalent to) one step solution normal equations

Two overlapping networks – Two step solution normal equations Use of same weights as in the (equivalent to) one step solution normal equations Recall that

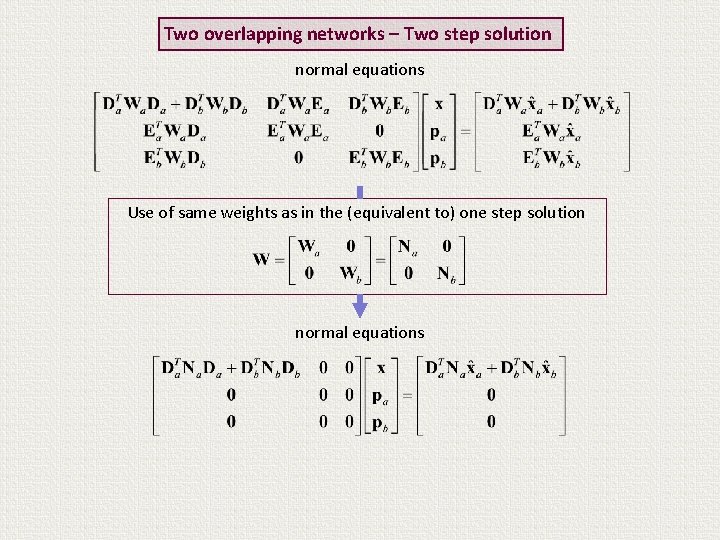
Two overlapping networks – Two step solution normal equations Use of same weights as in the (equivalent to) one step solution normal equations Vanishing terms

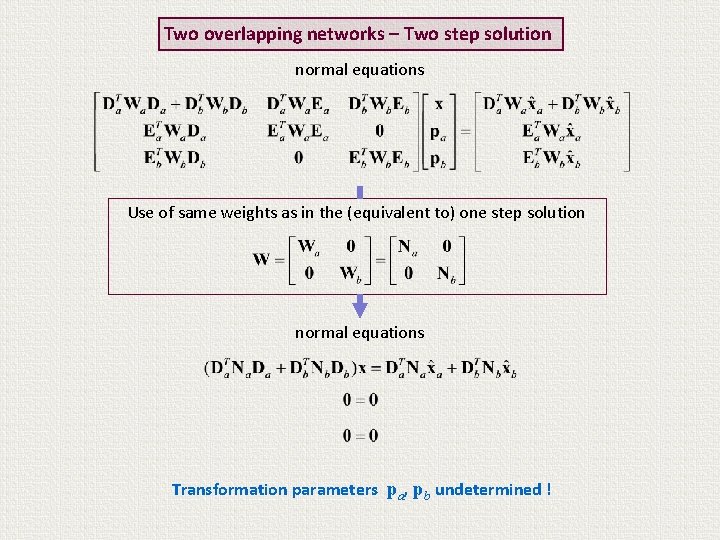
Two overlapping networks – Two step solution normal equations Use of same weights as in the (equivalent to) one step solution normal equations

Two overlapping networks – Two step solution normal equations Use of same weights as in the (equivalent to) one step solution normal equations Transformation parameters pa, pb undetermined !

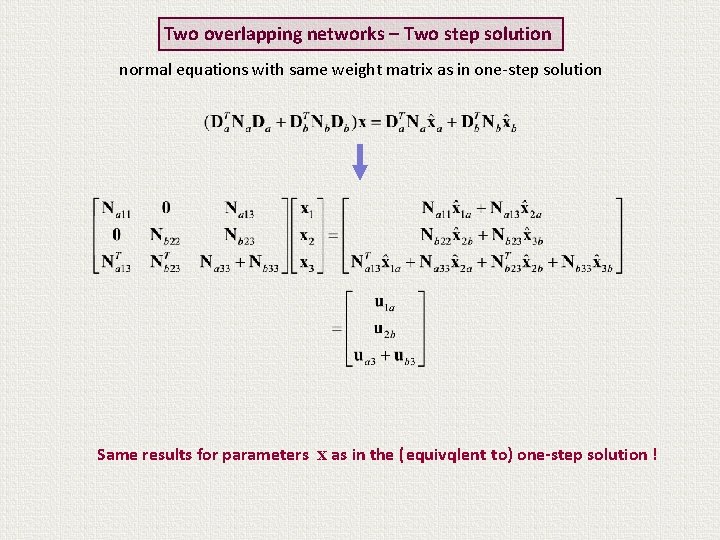
Two overlapping networks – Two step solution normal equations with same weight matrix as in one-step solution Same results for parameters x as in the (equivqlent to) one-step solution !

Two overlapping networks (equivalent to) one step solution “wrong” model ! Ignores that partial and final solutions are in different reference systems Two step solution correct model ! Treats partial and final solutions in different reference systems Normal equations with same weight matrices Same results for IERS parameters x ! Transformation parameters pa, pb undetermined !

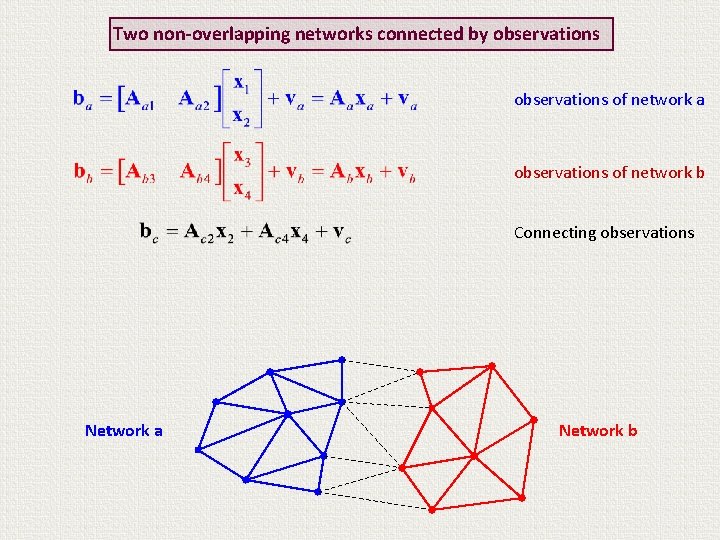
Two non-overlapping networks connected by observations This case applies to the ITRF formulation problem (with error-affected connecting observations at collocation sites)

Two non-overlapping networks connected by observations of network a observations of network b Connecting observations Network a Network b

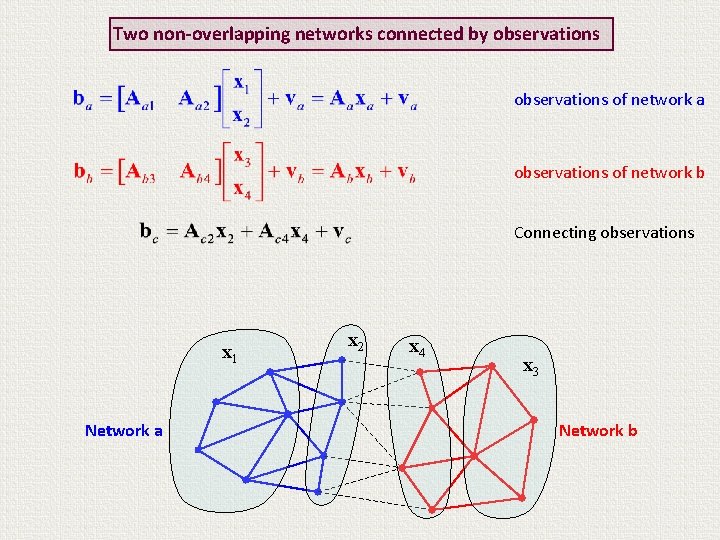
Two non-overlapping networks connected by observations of network a observations of network b Connecting observations x 1 Network a x 2 x 4 x 3 Network b

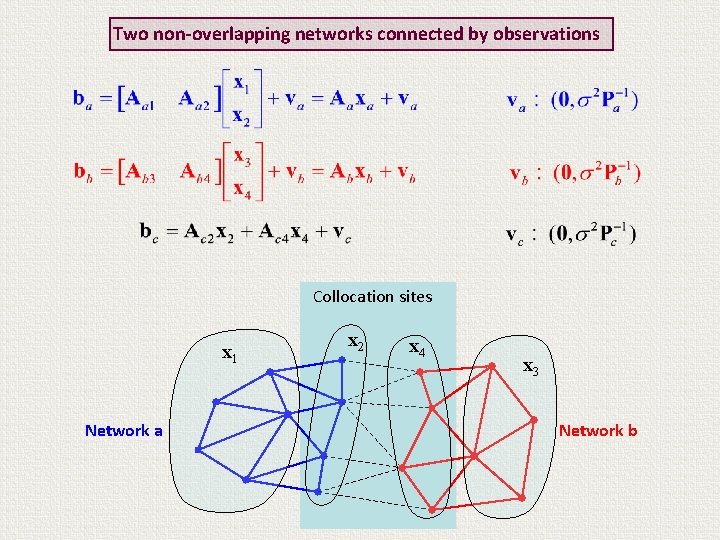
Two non-overlapping networks connected by observations Collocation sites x 1 Network a x 2 x 4 x 3 Network b

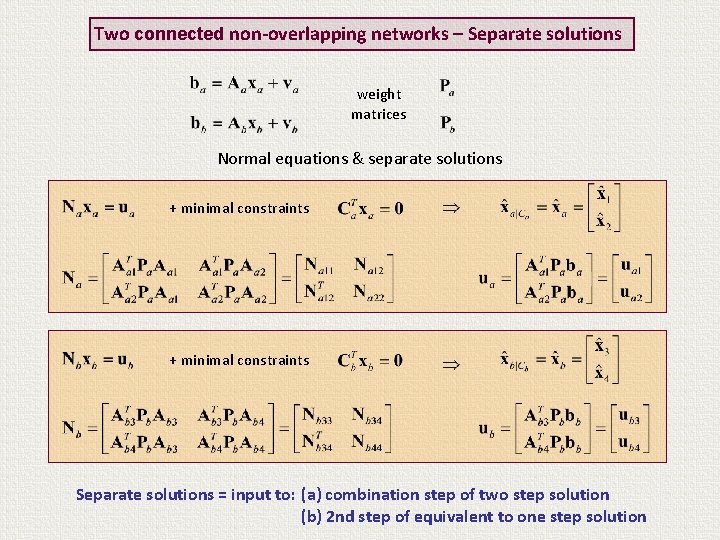
Two connected non-overlapping networks – Separate solutions weight matrices Normal equations & separate solutions + minimal constraints Separate solutions = input to: (a) combination step of two step solution (b) 2 nd step of equivalent to one step solution

Two connected non-overlapping networks – One step solution Joint treatment of observations from network a network b & connecting observations

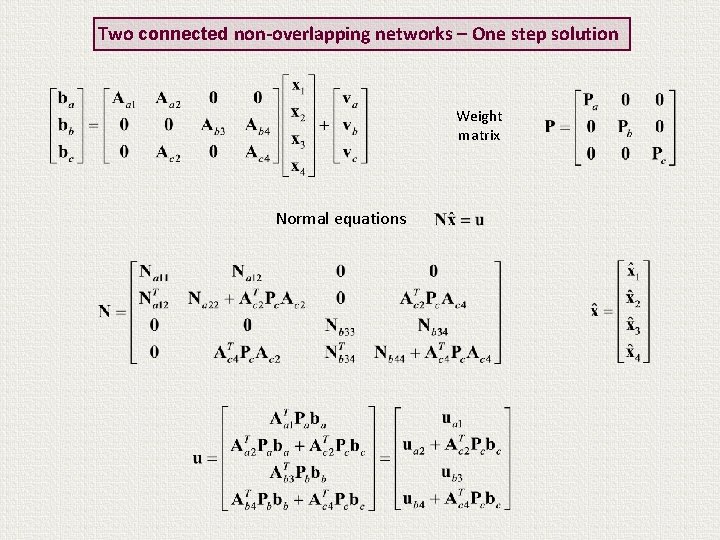
Two connected non-overlapping networks – One step solution Weight matrix Normal equations

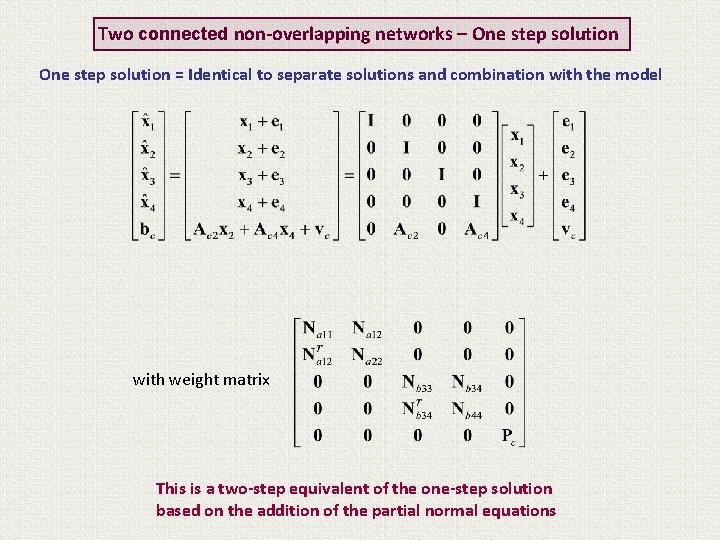
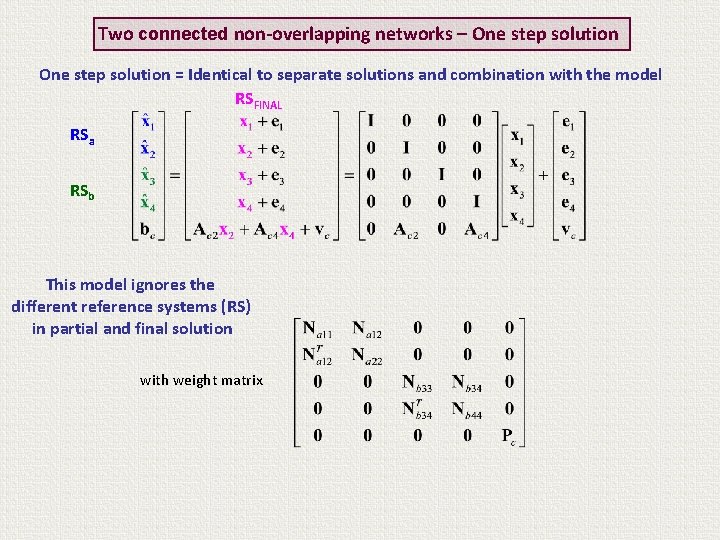
Two connected non-overlapping networks – One step solution = Identical to separate solutions and combination with the model with weight matrix This is a two-step equivalent of the one-step solution based on the addition of the partial normal equations

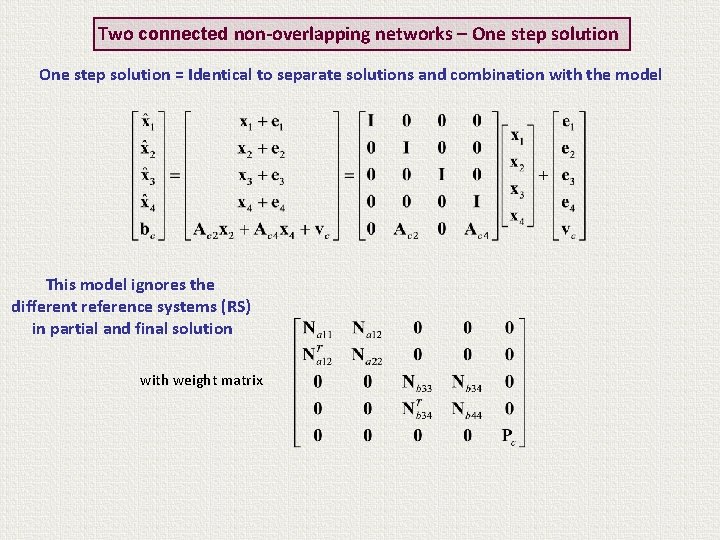
Two connected non-overlapping networks – One step solution = Identical to separate solutions and combination with the model This model ignores the different reference systems (RS) in partial and final solution with weight matrix

Two connected non-overlapping networks – One step solution = Identical to separate solutions and combination with the model RSFINAL RSa RSb This model ignores the different reference systems (RS) in partial and final solution with weight matrix

Two connected non-overlapping networks – Two step solution We have already treated the first step (separate solutions) It remains to examine the second combination step

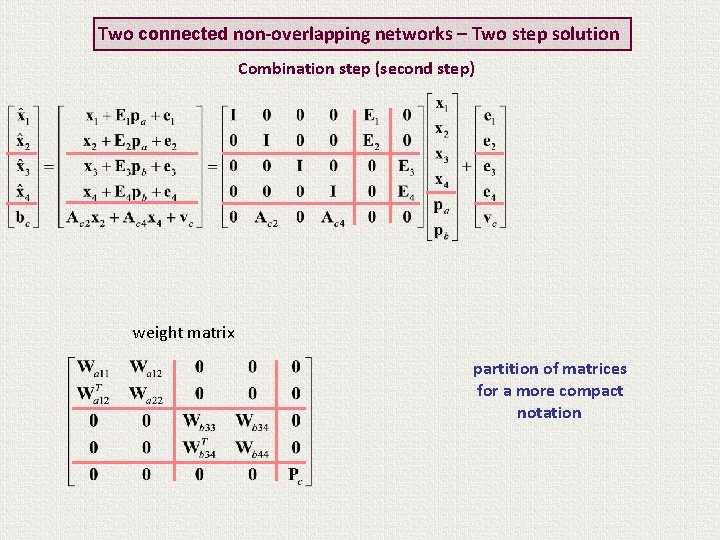
Two connected non-overlapping networks – Two step solution Combination step (second step) weight matrix

Two connected non-overlapping networks – Two step solution Combination step (second step) This model takes into account the different reference systems (RS) in partial and final solutions by introducing transformation parameters pa, pb weight matrix

Two connected non-overlapping networks – Two step solution Combination step (second step) weight matrix partition of matrices for a more compact notation

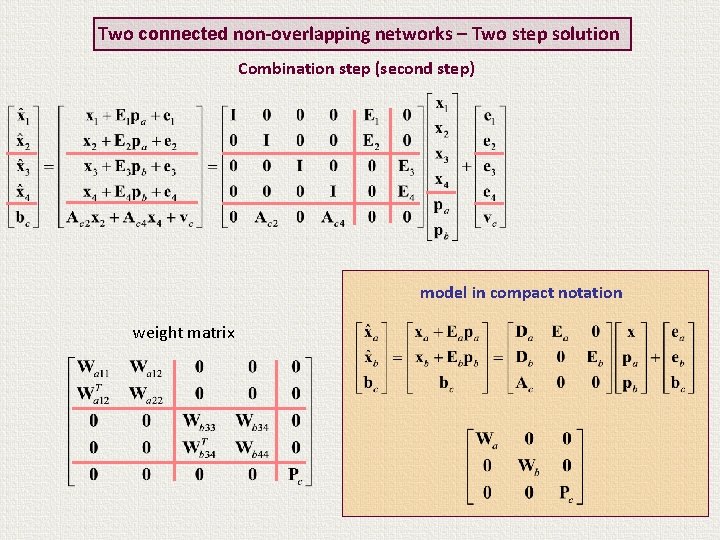
Two connected non-overlapping networks – Two step solution Combination step (second step) model in compact notation weight matrix

Two connected non-overlapping networks – Two step solution Combination step (second step) weight matrix

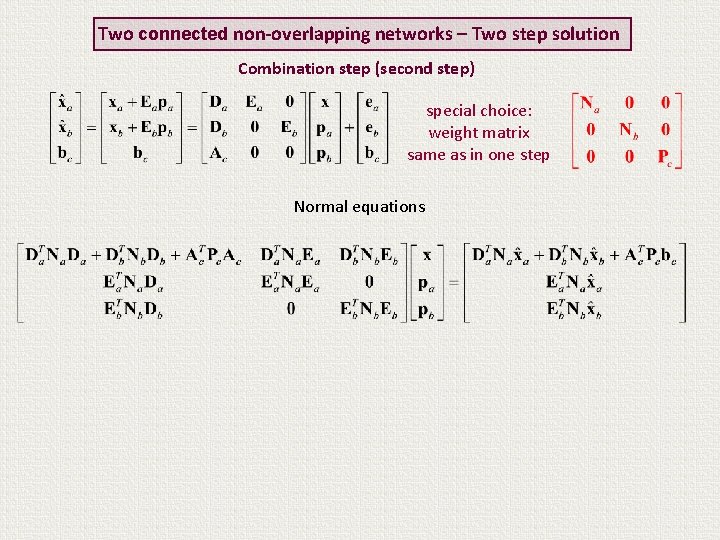
Two connected non-overlapping networks – Two step solution Combination step (second step) weight matrix Normal equations

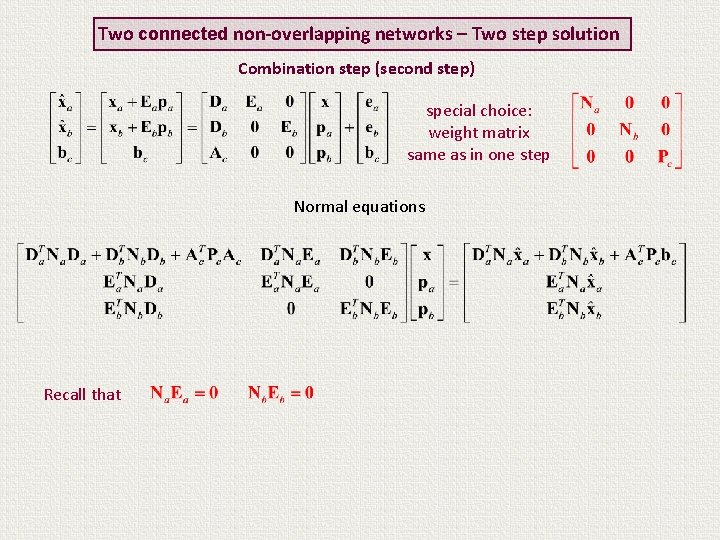
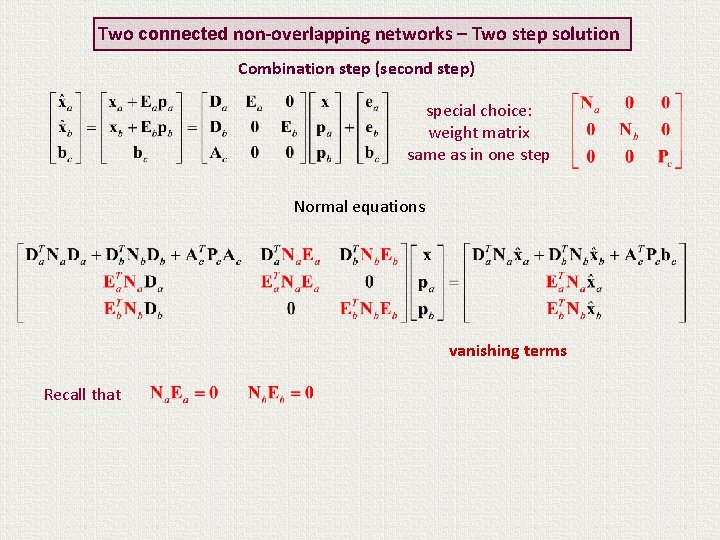
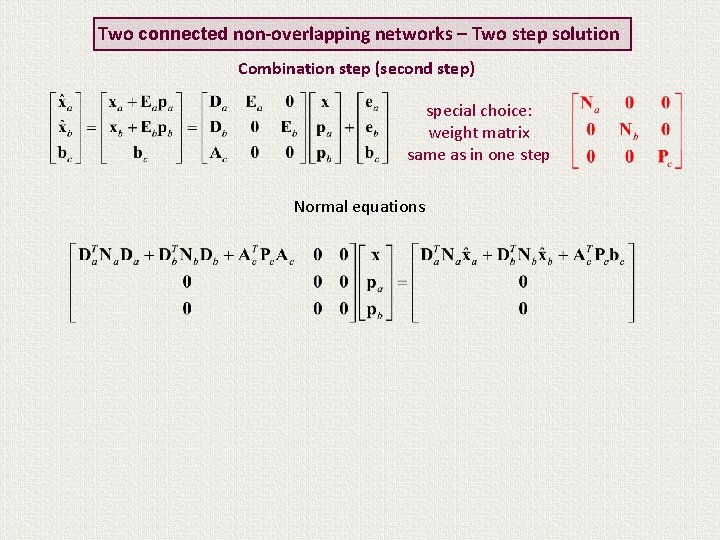
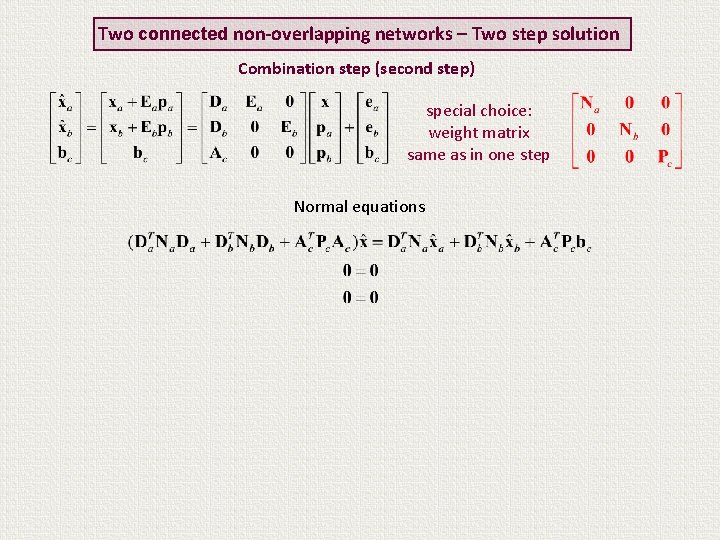
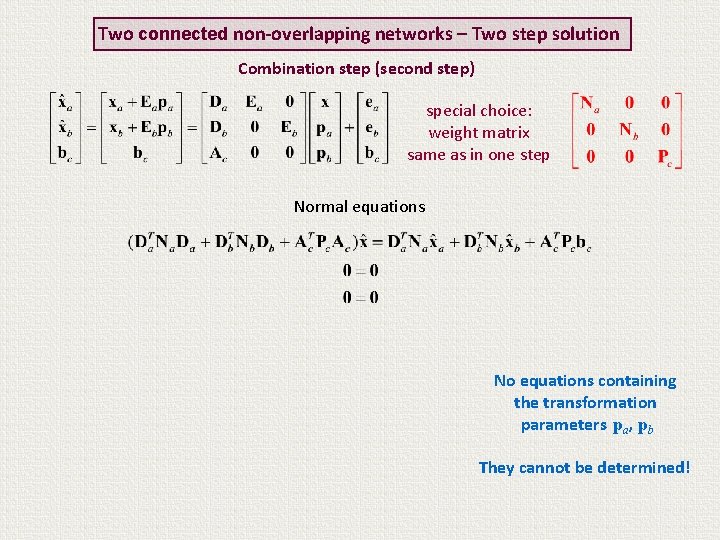
Two connected non-overlapping networks – Two step solution Combination step (second step) special choice: weight matrix same as in one step Normal equations

Two connected non-overlapping networks – Two step solution Combination step (second step) special choice: weight matrix same as in one step Normal equations Recall that

Two connected non-overlapping networks – Two step solution Combination step (second step) special choice: weight matrix same as in one step Normal equations vanishing terms Recall that

Two connected non-overlapping networks – Two step solution Combination step (second step) special choice: weight matrix same as in one step Normal equations

Two connected non-overlapping networks – Two step solution Combination step (second step) special choice: weight matrix same as in one step Normal equations

Two connected non-overlapping networks – Two step solution Combination step (second step) special choice: weight matrix same as in one step Normal equations No equations containing the transformation parameters pa, pb They cannot be determined!

Two connected non-overlapping networks – Two step solution Combination step (second step) special choice: weight matrix same as in one step Normal equations Identical to those of the one-step solution

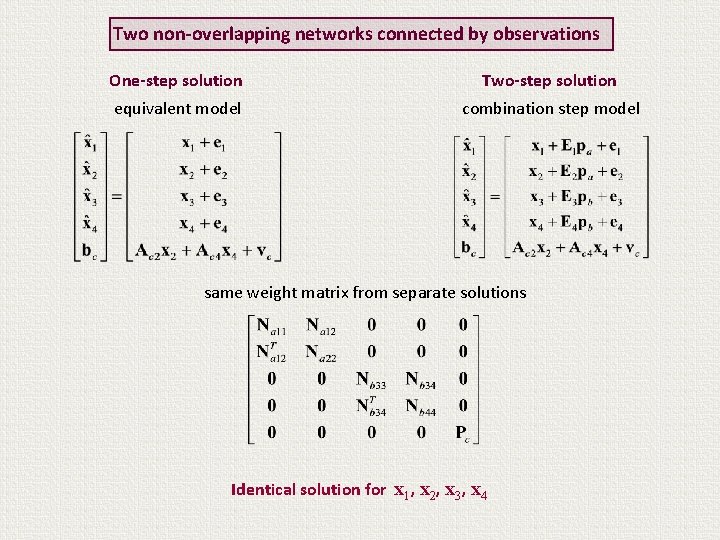
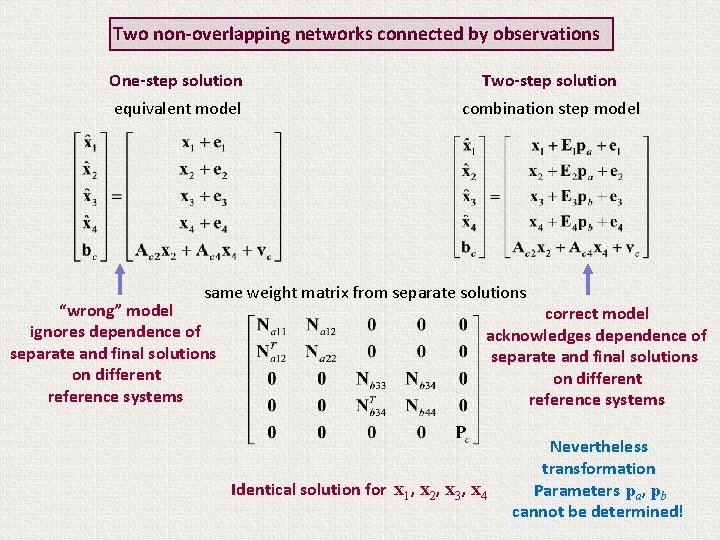
Two non-overlapping networks connected by observations One-step solution Two-step solution equivalent model combination step model same weight matrix from separate solutions Identical solution for x 1, x 2, x 3, x 4

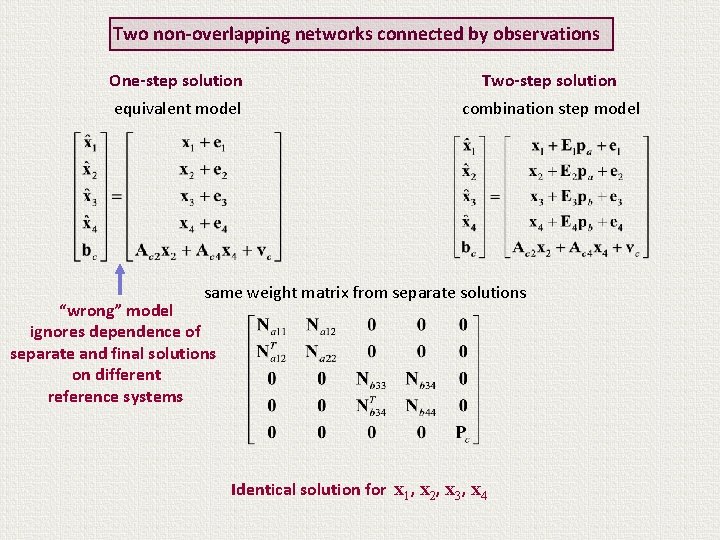
Two non-overlapping networks connected by observations One-step solution Two-step solution equivalent model combination step model same weight matrix from separate solutions “wrong” model ignores dependence of separate and final solutions on different reference systems Identical solution for x 1, x 2, x 3, x 4

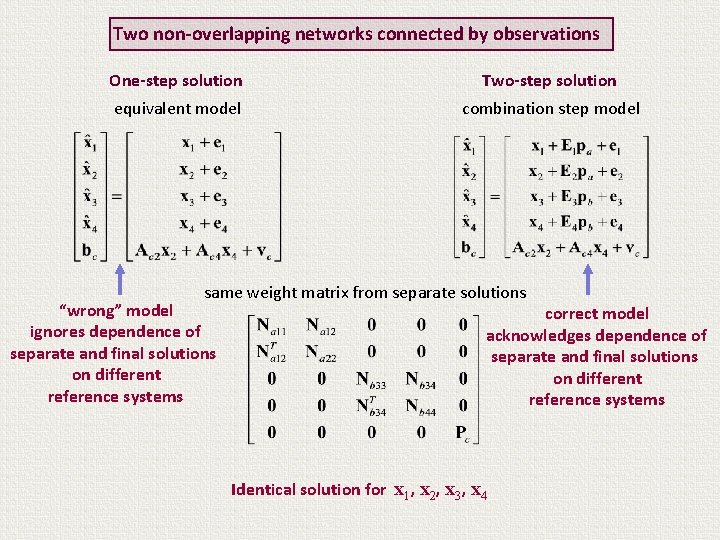
Two non-overlapping networks connected by observations One-step solution Two-step solution equivalent model combination step model same weight matrix from separate solutions “wrong” model ignores dependence of separate and final solutions on different reference systems correct model acknowledges dependence of separate and final solutions on different reference systems Identical solution for x 1, x 2, x 3, x 4

Two non-overlapping networks connected by observations One-step solution Two-step solution equivalent model combination step model same weight matrix from separate solutions “wrong” model ignores dependence of separate and final solutions on different reference systems correct model acknowledges dependence of separate and final solutions on different reference systems Identical solution for x 1, x 2, x 3, x 4 Nevertheless transformation Parameters pa, pb cannot be determined!

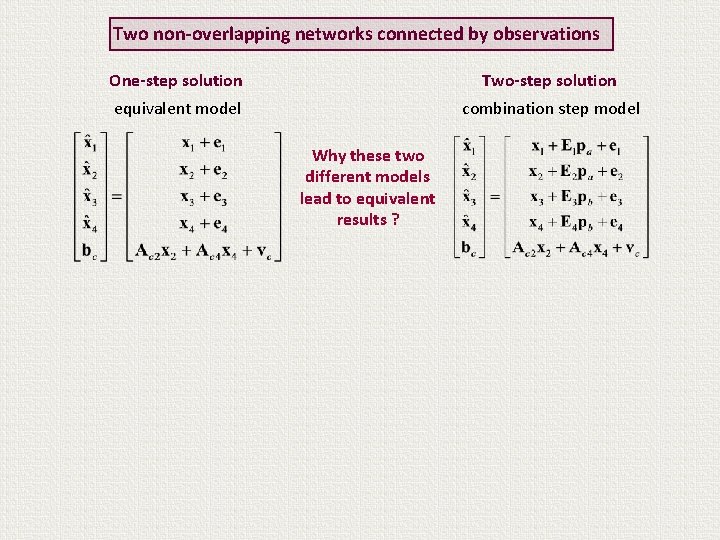
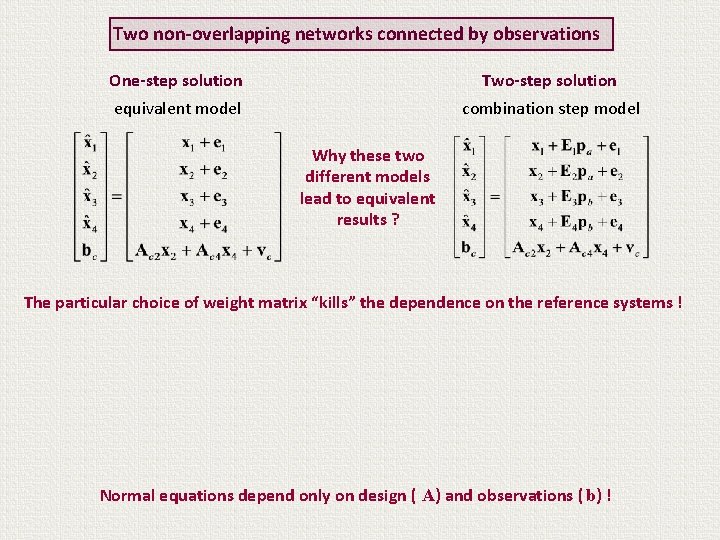
Two non-overlapping networks connected by observations One-step solution Two-step solution equivalent model combination step model Why these two different models lead to equivalent results ?

Two non-overlapping networks connected by observations One-step solution Two-step solution equivalent model combination step model Why these two different models lead to equivalent results ? The particular choice of weight matrix “kills” the dependence on the reference systems ! Normal equations depend only on design ( A) and observations ( b) !

The choice of weight problem In the two step approach, the first step produces singular covariance matrices. Therefore the weight matrices to be used in the second step are not uniquely defined. This fact raises some questions about the choice of weight matrices:

The choice of weight problem In the two step approach, the first step produces singular covariance matrices. Therefore the weight matrices to be used in the second step are not uniquely defined. This fact raises some questions about the choice of weight matrices: Are the weight matrices used in order to obtain equivalent results with the one step approach the correct ones? (Do they lead to BLUUE estimates? ) Yes !

The choice of weight problem In the two step approach, the first step produces singular covariance matrices. Therefore the weight matrices to be used in the second step are not uniquely defined. This fact raises some questions about the choice of weight matrices: Are the weight matrices used in order to obtain equivalent results with the one step approach the correct ones? (Do they lead to BLUUE estimates? ) Yes ! Are there other correct weight matrices? Yes !

The choice of weight problem In the two step approach, the first step produces singular covariance matrices. Therefore the weight matrices to be used in the second step are not uniquely defined. This fact raises some questions about the choice of weight matrices: Are the weight matrices used in order to obtain equivalent results with the one step approach the correct ones? (Do they lead to BLUUE estimates? ) Yes ! Are there other correct weight matrices? Yes ! Do different correct weight matrices lead to the same results? (i. e. to estimates that are connected by a change of the reference system) Yes !

The choice of weight problem Rao’s Unified Theory for singular covariance matrix and rank deficient design matrix Weight matrix to use: V = symmetric matrix such that:

The choice of weight problem Rao’s Unified Theory for singular covariance matrix and rank deficient design matrix Weight matrix to use: V = symmetric matrix such that: Our case: Combination step with V satisfying: Different weight matrices: from different choices of V and of the generalized inverse

Conclusions Under the Gauss-Markov assumptions (zero mean noise, single unknown reference variance) • Both the one-step and the two-step approaches give equivalent results when the used weight matrices are the normal equation matrices from the separate solutions. • The inclusion of reference frame transformation parameters is meaningless in this case. • The combination step must be modified to the addition of partial normal equations.

Conclusions Under the Gauss-Markov assumptions (zero mean noise, single unknown reference variance) • Both the one-step and the two-step approaches give equivalent results when the used weight matrices are the normal equation matrices from the separate solutions. • The inclusion of reference frame transformation parameters is meaningless in this case. • The combination step must be modified to the addition of partial normal equations. Suggestions for further study Beyond the Gauss-Markov assumptions (biases, different variance components) A future study of the effect of biases and the variance component estimation in the two alternative formulations is required. Different “correct” weight matrices in combination step A further study of the Rao’s unified theory as applies in our specific problem. Characterization of the whole class weight matrices giving the “same” solution.

Thanks for your attention ! A copy of this presentation can be downloaded from http: //der. topo. auth. gr/
 Lettre de motivation concours itrf
Lettre de motivation concours itrf Zuheir altamimi
Zuheir altamimi Rapport activité itrf
Rapport activité itrf Why problem formulation follow goal formulation
Why problem formulation follow goal formulation Approaches to formulation of accounting theory
Approaches to formulation of accounting theory Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Dot
Dot Bổ thể
Bổ thể Nguyên nhân của sự mỏi cơ sinh 8
Nguyên nhân của sự mỏi cơ sinh 8 độ dài liên kết
độ dài liên kết Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Chúa sống lại
Chúa sống lại điện thế nghỉ
điện thế nghỉ Một số thể thơ truyền thống
Một số thể thơ truyền thống Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Sơ đồ cơ thể người
Sơ đồ cơ thể người Số nguyên tố là
Số nguyên tố là Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới ưu thế lai là gì
ưu thế lai là gì Môn thể thao bắt đầu bằng chữ đua
Môn thể thao bắt đầu bằng chữ đua Tư thế ngồi viết
Tư thế ngồi viết Bàn tay mà dây bẩn
Bàn tay mà dây bẩn Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Cách giải mật thư tọa độ
Cách giải mật thư tọa độ Tư thế ngồi viết
Tư thế ngồi viết Thế nào là giọng cùng tên?
Thế nào là giọng cùng tên? Chó sói
Chó sói Thẻ vin
Thẻ vin Thể thơ truyền thống
Thể thơ truyền thống Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Hươu thường đẻ mỗi lứa mấy con
Hươu thường đẻ mỗi lứa mấy con Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Diễn thế sinh thái là
Diễn thế sinh thái là Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Lp html
Lp html Phép trừ bù
Phép trừ bù Lời thề hippocrates
Lời thề hippocrates Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Glasgow thang điểm
Glasgow thang điểm đại từ thay thế
đại từ thay thế Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Công thức tiính động năng
Công thức tiính động năng Khi nào hổ con có thể sống độc lập
Khi nào hổ con có thể sống độc lập Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Functional strategy in strategic management
Functional strategy in strategic management Definition of transportation problem
Definition of transportation problem Secure attachment style
Secure attachment style Csp sudoku
Csp sudoku Problem formulation examples
Problem formulation examples Formulation of lpp examples
Formulation of lpp examples Functional strategies in strategic management
Functional strategies in strategic management Question formulation technique pdf
Question formulation technique pdf Cross product moment
Cross product moment Scope and limitation example
Scope and limitation example Research design formulation
Research design formulation Case formulation cbt example
Case formulation cbt example Variational calculus
Variational calculus Secondary surfactant in shampoo
Secondary surfactant in shampoo What is program logic formulation
What is program logic formulation Beck longitudinal formulation 1979
Beck longitudinal formulation 1979 Wuffda feed formulation
Wuffda feed formulation Case conceptualization cbt
Case conceptualization cbt 5 ps formulation
5 ps formulation Leaker test for parenterals
Leaker test for parenterals Process of budget formulation
Process of budget formulation Question formulation technique
Question formulation technique Problem
Problem Belief driven formulation worksheet
Belief driven formulation worksheet Monophasic liquid can be given for
Monophasic liquid can be given for Formulation of eye drops
Formulation of eye drops Shrm vs hrm
Shrm vs hrm Preemptive goal programming
Preemptive goal programming Serial polyadic dp formulation
Serial polyadic dp formulation Ned plan
Ned plan Build execution into strategy
Build execution into strategy Process of plan formulation in nepal
Process of plan formulation in nepal Linear programming model formulation and graphical solution
Linear programming model formulation and graphical solution Qft questioning
Qft questioning Question focus technique
Question focus technique Cross product moment
Cross product moment