On Reducing the Global State Graph for Verification

On Reducing the Global State Graph for Verification of Distributed Computations Vijay K. Garg, Arindam Chakraborty Parallel and Distributed Systems Laboratory The University of Texas at Austin

Roadmap n n n Motivation Background: Lattice Theory Interval Clocks and Congruences Detecting CTL-X predicates Optimal Congruence construction Conclusion

Motivation: Reliable Systems n Concurrent systems are prone to errors. q Concurrency, nondeterminism, process and channel failures Techniques to ensure correctness n Model Checking and Formal Verification q n Exponential complexity Testing and Debugging
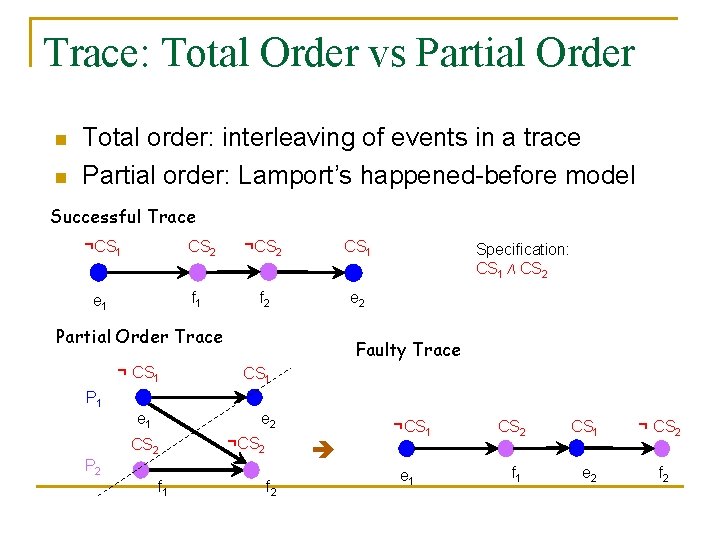
Trace: Total Order vs Partial Order n n Total order: interleaving of events in a trace Partial order: Lamport’s happened-before model Successful Trace ¬CS 1 CS 2 f 1 e 1 ¬CS 2 CS 1 f 2 e 2 Partial Order Trace ¬ CS 1 Specification: CS 1 Λ CS 2 Faulty Trace CS 1 P 1 e 2 CS 2 ¬CS 2 P 2 f 1 f 2 ¬CS 1 e 1 CS 2 CS 1 ¬ CS 2 f 1 e 2 f 2
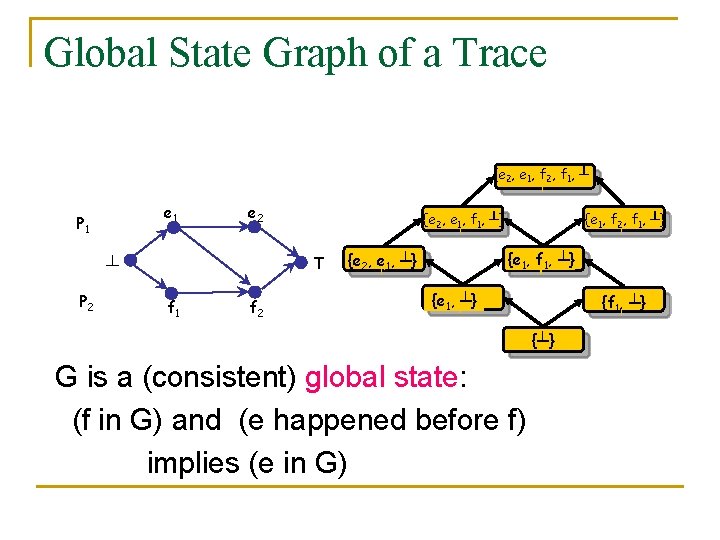
Global State Graph of a Trace {e 2, e 1, f 2, f 1, ┴ e 1 P 1 e 2 ┴ P 2 {e 2, e 1, f 1, ┴} T f 1 f 2 {e 1, f 2, f 1, ┴} {e 1, f 1, ┴} {e 2, e 1, ┴} {f 1, ┴} {┴} G is a (consistent) global state: (f in G) and (e happened before f) implies (e in G)

Problem Statement n Given q q n Determine: q n a partially ordered trace a temporal logic formula if the formula is true in the graph of the global states of the trace Examples: q q EF: CS(1) / CS(2) AG: (request(i) => AF: lock(i))
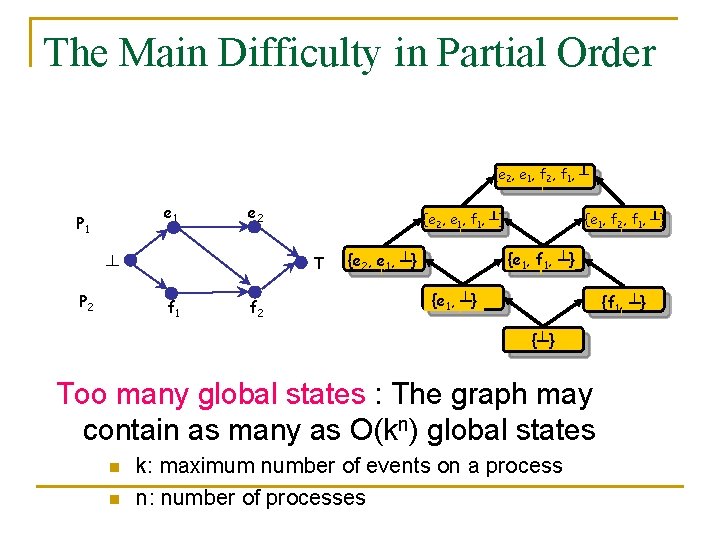
The Main Difficulty in Partial Order {e 2, e 1, f 2, f 1, ┴ e 1 P 1 e 2 ┴ P 2 {e 2, e 1, f 1, ┴} T f 1 f 2 {e 1, f 2, f 1, ┴} {e 1, f 1, ┴} {e 2, e 1, ┴} {f 1, ┴} {┴} Too many global states : The graph may contain as many as O(kn) global states n n k: maximum number of events on a process n: number of processes

Reducing the Global State Graph n n Idea: Reduce the global state graph w. r. t the formula that needs to be verified Example: [Alagar, Venkatesan 01] q n To detect a formula of the form EF: B it is sufficient to track only those variables that affect B B: non-temporal formula (e. g. x > y) This paper: q How do we extend this result to CTL-X ?
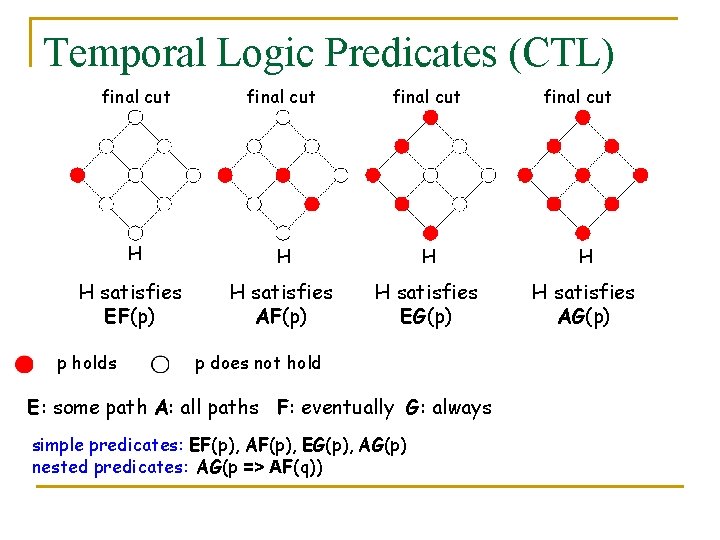
Temporal Logic Predicates (CTL) final cut H H H satisfies EF(p) H satisfies AF(p) H satisfies EG(p) H satisfies AG(p) p holds p does not hold E: some path A: all paths F: eventually G: always simple predicates: EF(p), AF(p), EG(p), AG(p) nested predicates: AG(p => AF(q)) final cut

Temporal Logic CTL-X n n n CTL Operators: EF, AF, EG, AG, EU, AU and X. X (next-time) is not preserved by state reductions, hence focus on CTL without X Example: , ”once a process requests a lock then it eventually gets the lock”, can be expressed as EG, AG and AU can be expressed in terms of EF, AF and EU Allows specification of path properties
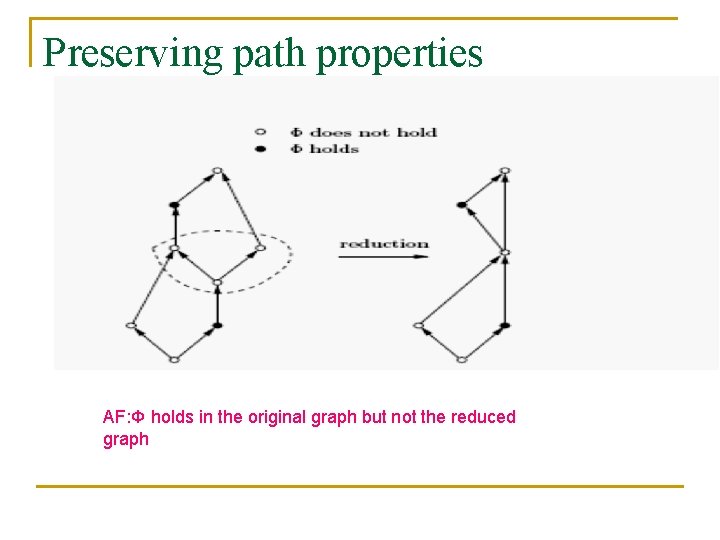
Preserving path properties AF: Φ holds in the original graph but not the reduced graph

Our Approach n n n Uses the fact that global state graph is a lattice Put constraints on the global states that can be merged so that path properties preserved Key result q If the global states are combined using lattice congruences then path properties are preserved
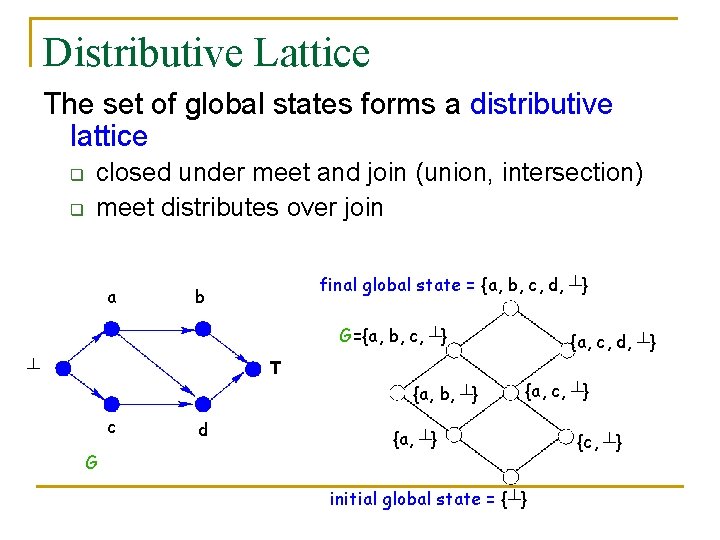
Distributive Lattice The set of global states forms a distributive lattice q q closed under meet and join (union, intersection) meet distributes over join a final global state = {a, b, c, d, ┴} b G={a, b, c, ┴} ┴ Τ {a, b, ┴} c G d {a, c, d, ┴} {a, c, ┴} {a, ┴} initial global state = {┴} {c, ┴}
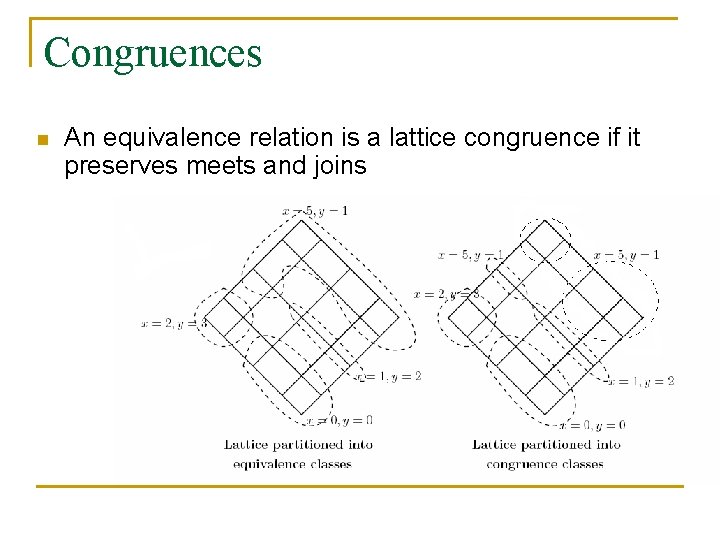
Congruences n An equivalence relation is a lattice congruence if it preserves meets and joins
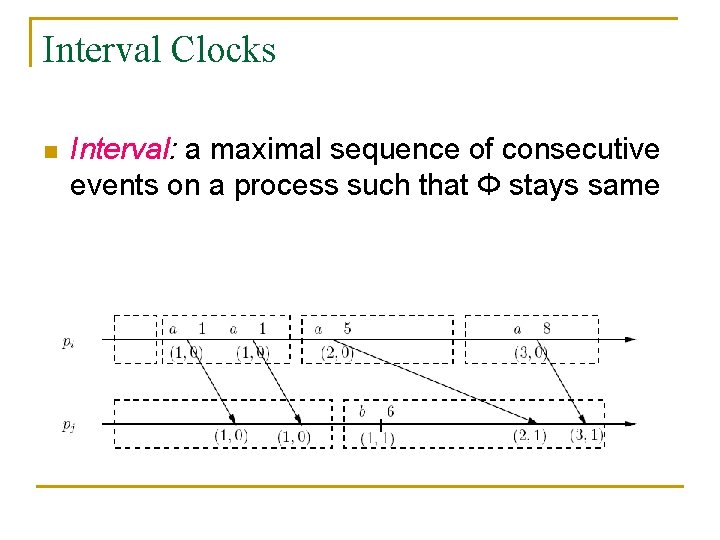
Interval Clocks n Interval: a maximal sequence of consecutive events on a process such that Φ stays same
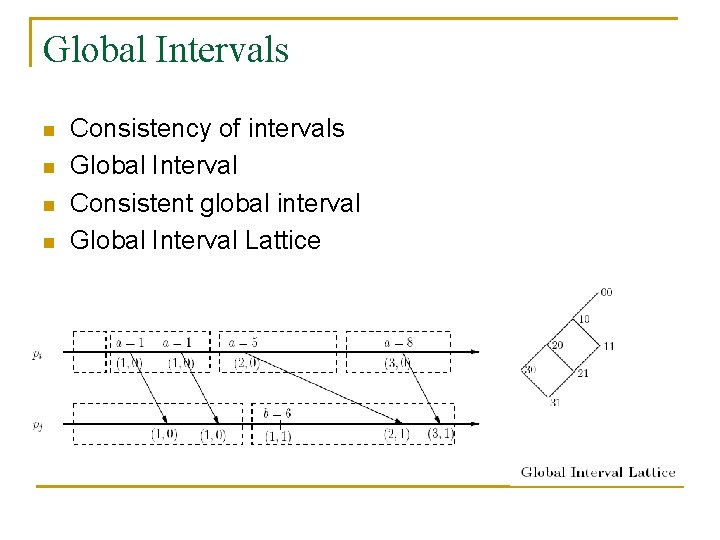
Global Intervals n n Consistency of intervals Global Interval Consistent global interval Global Interval Lattice
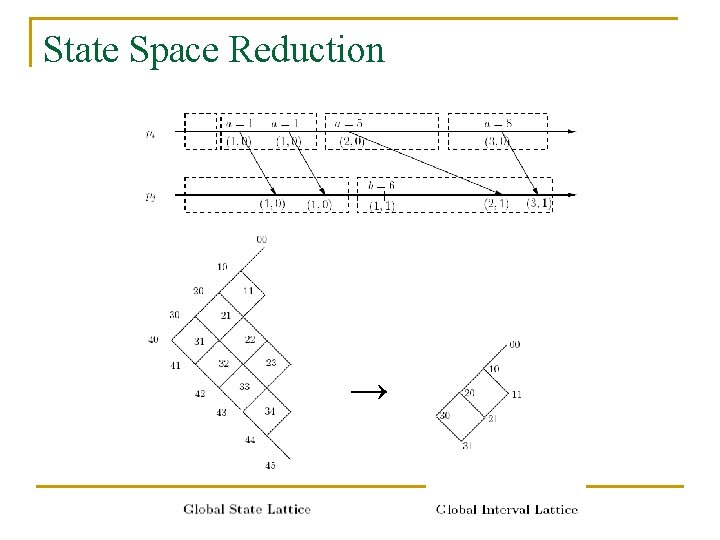
State Space Reduction →
![Intervals and Congruences n Theorem [Alagar, Venkatesan 01]: There exists a global interval at Intervals and Congruences n Theorem [Alagar, Venkatesan 01]: There exists a global interval at](http://slidetodoc.com/presentation_image_h2/de60c409b491913fe75d31a8f0d15568/image-18.jpg)
Intervals and Congruences n Theorem [Alagar, Venkatesan 01]: There exists a global interval at which a predicate Φ is true if and only if there exists a global state at which Φ is true n Hence interval clocks can be used to detect EF: B n Result [this paper]: The global interval lattice formed by interval clocks is a reduced lattice modulo a congruence relation.

Detecting Temporal Formulae with Intervals n n n B : any non-temporal formula. θ : any lattice congruence that refines the equivalence class induced by B. Theorem: AF: B holds in a lattice L iff AF: B holds in L/θ n Key Lemma [Equivalence of Paths]: For any path in L, there exists an “equivalent” path in L/θ and vice-versa. n Theorem: E: B 1 U B 2 holds in a lattice L iff E: B 1 U B 2 holds in L/θ. (Note: EG, AG and AU can be expressed in terms of AF, EF and EU)

Optimal Congruence n Using interval clocks, q q q n Disadvantage: q n an online algorithm for state space reduction Intervals can be computed locally by each process A process reports only the relevant events to the monitor process Does not give the optimal congruence since each process decides locally Centralized Model: q q q each process reports every event to the monitor. The monitor process has information from every process compute exactly which global states need to be added

Optimal Congruence n Principal Congruence: Given two elements a, b in L, the smallest congruence that puts a and b in the same congruence class is called the principal congruence of a and b, denoted n Theorem: Given a lattice L and an equivalence relation E on L, the largest congruence that is contained in E is given by: n x in J(L) if there exists an event e such that x is the least global state that contains e, x* = x – {e}.

Algorithm

Conclusions n using congruences for the state space explosion problem q q n n Induce equivalence on the global state graph by the value of the properties evaluated at each state find the largest congruence that is contained in this equivalence relation Extended property verification using reduced lattices to CTL−X An algorithm to compute the optimal congruence

Q&A and thanks!

Nested Temporal Formulae n n n Handle nested temporal formulae using the recursive subformulae evaluation technique of model checking Say we want to verify Interval Clocks will be based on non-temporal predicates p, r Model checking algorithms evaluate nested temporal formulae on the global state graph by recursively evaluating all sub-formulae. Given the global interval graph G and the formula Φ, model checking algorithms will return the set of all states which satisfy Φ (say [Φ]). We modify model checking so that along with returning [Φ], it also simultaneously labels each state s on the graph by whether Φ is true at s or not.

Algorithm 1. Find the set S of all sub-formulae without temporal operators, from the set of properties to be verified on the computation 2. Create the global interval lattice L from the computation by using interval clocks with respect to the set S 3. Run model checking algorithm on L with the modification that states are labeled in each step as described earlier. Nested temporal formulae, due to state labeling of sub-formulae, can be treated as simple unnested temporal formulae.
- Slides: 26