On necessary and sufficient cryptographic assumptions the case







































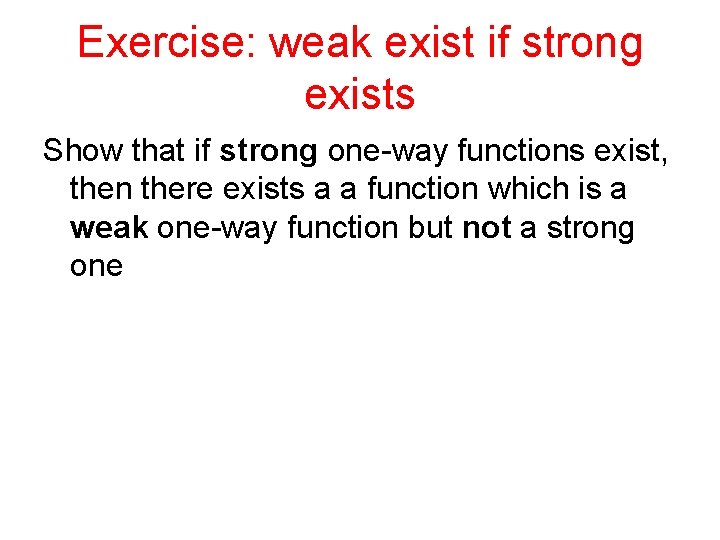




![Probability of Success • Define S={y=f(x) | Prob[Inner loop successful| y ] > β} Probability of Success • Define S={y=f(x) | Prob[Inner loop successful| y ] > β}](https://slidetodoc.com/presentation_image/e9b6aa89e8b2ec2a153b90c30c42cf5b/image-47.jpg)

![S is the only success. . But Prob[B[y 1, y 2] g-1(y 1, y S is the only success. . But Prob[B[y 1, y 2] g-1(y 1, y](https://slidetodoc.com/presentation_image/e9b6aa89e8b2ec2a153b90c30c42cf5b/image-49.jpg)
![Contradiction But Prob[(y 1, y 2) P and y 1, y 2 S] ≤ Contradiction But Prob[(y 1, y 2) P and y 1, y 2 S] ≤](https://slidetodoc.com/presentation_image/e9b6aa89e8b2ec2a153b90c30c42cf5b/image-50.jpg)











- Slides: 62

On necessary and sufficient cryptographic assumptions: the case of memory checking Lecture 1: One-way functions Lecturer: Moni Naor Weizmann Institute of Science

What is Cryptography? Traditionally: how to maintain secrecy in communication Alice and Bob talk while Eve tries to listen Bob Alice Eve

History of Cryptography • Very ancient occupation • Many interesting books and sources, especially about the Enigma – David Kahn, The Codebreakers, 1967 – Gaj and Orlowski, Facts and Myths of Enigma: Breaking Stereotypes, Eurocrypt 2003 • Not the subject of these talks

Modern Times • Up to the mid 70’s - mostly classified military work – Exception: Shannon, Turing* • Since then - explosive growth – Commercial applications – Scientific work: tight relationship with Computational Complexity Theory – Major works: Diffie-Hellman, Rivest, Shamir and Adleman (RSA) • Recently - more involved models for more diverse tasks.

Cryptography and Complexity Theory • Study the resources needed to solve computational problems Cryptography • Find ways to specify security requirements of systems • Use the – computer time, computational memory infeasibility of • Identify problems that problems in order to are infeasible to obtain security. compute. The development of these two areas is tightly connect

Key Idea of Cryptography Use the intractability of some problems for the advantage of constructing secure system Almost any cryptographic task requires using this idea. Our goal is to investigate the tasks of memory checking and sublinear authentication and see whether they require it

Lectures Outline • One-way functions and their essential role in cryptography – The authentication problem • Communication Complexity • Memory Checking • Lower bound for memory checking and authentication

Three Basic Issues in Cryptography • Identification • Authentication • Encryption – Won’t discuss much

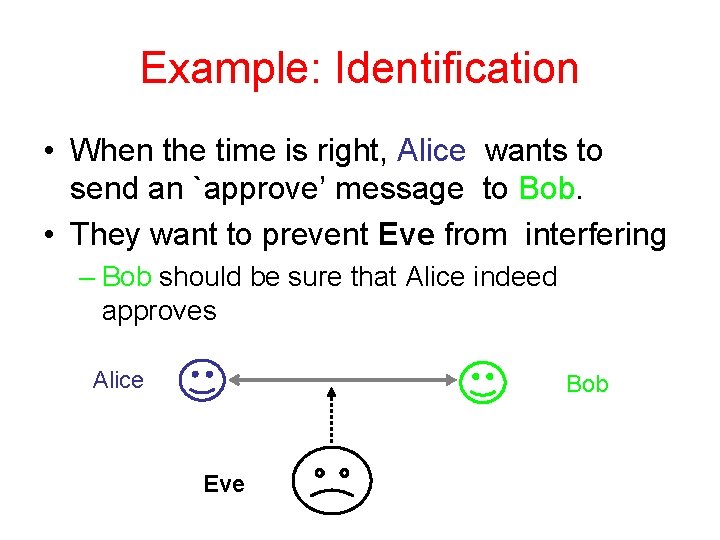
Example: Identification • When the time is right, Alice wants to send an `approve’ message to Bob. • They want to prevent Eve from interfering – Bob should be sure that Alice indeed approves Alice Bob Eve

Rigorous Specification of Security To define security of a system must specify: 1. What constitute a failure of the system 2. The power of the adversary – computational – access to the system – what it means to break the system.

Specification of the Problem Alice and Bob communicate through a channel Bob has two external states {N, Y} N, Y Eve completely controls the channel Requirements: • If Alice wants to approve and Eve does not interfere – Bob moves to state Y • If Alice does not approve, then for any behavior from Eve, Bob stays in N • If Alice wants to approve and Eve does interfere - no requirements from the external state

Can we guarantee the requirements? • No – when Alice wants to approve she sends (and receives) a finite set of bits on the channel. Eve can guess them. • To the rescue - probability. – Want that Eve will succeed only with low probability. – How low? Related to the string length that Alice sends…

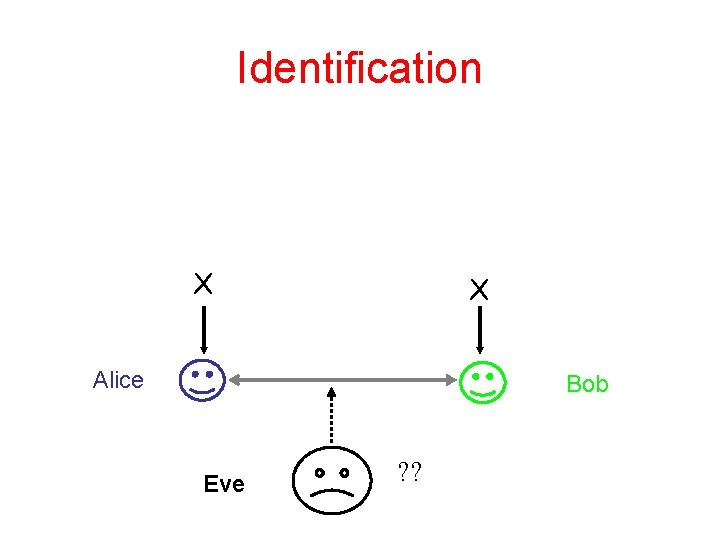
Identification X X Alice Bob Eve ? ?

Suppose there is a setup period • There is a setup where Alice and Bob can agree on a common secret – Eve only controls the channel, does not see the internal state of Alice and Bob (only external state of Bob) Simple solution: – Alice and Bob choose a random string X R {0, 1}n – When Alice wants to approve – she sends X – If Bob gets any symbols on channel – compares to X • If equal moves to Y

Eve’s probability of success • If Alice did not send X and Eve put some string X’ on the channel, then – Bob moves to Y only if X= X’ Prob[X=X’] ≤ 2 -n Good news: can make it a small as we wish • What to do if Alice and Bob cannot agree on a uniformly generated string X?

Less than perfect random variables • Suppose X is chosen according to some distribution Px over some set of symbols Γ • What is Eve’s best strategy? • What is her probability of success

(Shannon) Entropy Let X be random variable over alphabet Γ with distribution Px The (Shannon) entropy of X is H(X) = - ∑ x Γ Px (x) log Px (x) Where we take 0 log 0 to be 0. Represents how much we can compress X

Examples • If X=0 (constant) then H(x) = 0 – Only case where H(x) = 0 is when x is constant – All other cases H(x) >0 • If X {0, 1} and Prob[X=0] = p and Prob[X=1]=1 -p, then H(X) = -p log p + (1 -p) log (1 -p) ≡ H(p) If X {0, 1}n and is uniformly distributed, then H(X) = - ∑ n 1/2 n log 1/2 n = 2 n/2 n n = n

Properties of Entropy • Entropy is bounded H(X) ≤ log | Γ | with equality only if X is uniform over Γ

Does High Entropy Suffice for Identification? • If Alice and bob agree on X {0, 1}n where X has high entropy (say H(X) ≥ n/2 ), what are Eve’s chances of cheating? • Can be high: say – Prob[X=0 n ] = 1/2 – For any x 1{0, 1} n-1 Prob[X=x ] = 1/2 n Then H(X) = n/2+1/2 But Eve can cheat with probability at least ½ by guessing that X=0 n

Another Notion: Min Entropy Let X be random variable over alphabet Γ with distribution Px The min entropy of X is Hmin(X) = - log max x Γ Px (x) The min entropy represents the most likely value of X Property: Hmin(X) ≤ H(X) Why?

High Min Entropy and Passwords Claim: if Alice and Bob agree on such that Hmin(X) ≥ m, then the probability that Eve succeeds in cheating is at most 2 -m Proof: Make Eve deterministic, by picking her best choice, X’ = x’. Prob[X=x’] = Px (x’) ≤ max x Γ Px (x) =2 –Hmin(X) ≤ 2 -m Conclusion: passwords should be chosen to have high min-entropy!

Good source on Information Theory: T. Cover and J. A. Thomas, Elements of Information Theory

One-time vs. many times • This was good for a single identification. What about many sessions of identification? • Later…

A different scenario – now Charlie is involved • Bob has no proof that Alice indeed identified • If there are two possible verifiers, Bob and Charlie, they can each pretend to each other to be Alice – Can each have there own string – But, assume that they share the setup phase • Whatever Bob knows Charlie know • Relevant when they are many of possible verifiers!

The new requirement • If Alice wants to approve and Eve does not interfere – Bob moves to state Y • If Alice does not approve, then for any behavior from Eve and Charlie, Bob stays in N • Similarly if Bob and Charlie are switched Charlie Alice Bob Eve

Can we achieve the requirements? • Observation: what Bob and Charlie received in the setup phase might as well be public • Therefore can reduce to the previous scenario (with no setup)… • To the rescue - complexity Alice should be able to perform something that neither Bob nor Charlie (nor Eve) can do Must assume that the parties are not computationally all powerful!

Function and inversions • We say that a function f is hard to invert if given y=f(x) it is hard to find x’ such that y=f(x’) – x’ need not be equal to x – We will use f-1(y) to denote the set of preimages of y • To discuss hard must specify a computational model • Use two flavors: – Concrete

One-way functions - asymptotic A function f: {0, 1}* → {0, 1}* is called a one-way function, if • f is a polynomial-time computable function – Also polynomial relationship between input and output length • for every probabilistic polynomial-time algorithm A, every positive polynomial p(. ), and all sufficiently large n’s Prob[ A(f(x)) f-1(f(x)) ] ≤ 1/p(n) Where x is chosen uniformly in {0, 1}n and the probability is also over the internal coin flips of A

One-way functions – concrete version A function f: {0, 1}n → {0, 1}n is called a (t, ε) one-way function, if • f is a polynomial-time computable function (independent of t) • for every t-time algorithm A, Prob[A(f(x)) f-1(f(x)) ] ≤ ε Where x is chosen uniformly in {0, 1}n and the probability is also over the internal coin flips of A Can either think of t and ε as being fixed or as t(n), ε(n)

Complexity Theory and One-way Functions • Claim: if P=NP then there are no one-way functions Proof: for any one-way function f: {0, 1}n → {0, 1}n consider the language Lf : – Consisting of strings of the form {y, b 1, b 2, …, bk} – There is an x {0, 1}n such that y=f(x) and – The first k bits of x are b 1, b 2…bk Lf is NP – guess x and check If Lf is P then f is invertible in polynomial time: Self reducibility

A few properties and questions concerning one-way functions • Major open problem: connect the existence of one-way functions and the P=NP? • If f is one-to-one it is a called a one-way permutation. In what complexity class does the problem of inverting oneway permutations reside? – good exercise! • If f’ is a one-way function, is f’ where f’(x) is f(x) with the last bit chopped a one-way function? • If f is a one-way function, is f. L where f. L(x) consists of the first half of the bits of f(x) a one-way function? – good exercise! • If f is a one way function is g(x) = f(f(x)) necessarily a one-way function? – good exercise!

Solution to the password problem • Assume that – f: {0, 1}n → {0, 1}n is a (t, ε) one-way function – Adversary’s run times is bounded by t • Setup phase: – Alice chooses x R {0, 1}n – computes y=f(x) – Gives y to Bob and Charlie • When Alice wants to approve – she sends x • If Bob gets any symbols on channel – call them z; compute f(z) and compares to y – If equal moves to state Y – If not equal moves permanently to state N

Eve’s and Charlie’s probability of success • If Alice did not send x and Eve (Charlie) put some string x’ on the channel to Bob, then: – Bob moves to state Y only if f(x’)=y=f(x) – But we know that Prob[A[f(x)] f-1(f(x)) ] ≤ ε or. A’ else we can use Eve to break the one-way function y Ev yy e x’ x’ Good news: if ε can be made as small as we wish, then we have a good scheme. • • Can be used for monitoring Similar to the Unix password scheme – f(x) stored in login file – DES used as the one-way function.

Reductions • This is a simple example of a reduction • Simulate Eve’s algorithm in order to break the one-way function • Most reductions are much more involved

Cryptographic Reductions Show to use an adversary for breaking primitive 1 in order to break primitive 2 Important • Run time: how does T 1 relate to T 2 • Probability of success: how does 1 relate to 2 • Access to the system 1 vs. 2

Are one-way functions essential to the two guards password problem? • Precise definition: – for every probabilistic polynomial-time algorithm A controlling Eve and Charlie – every polynomial p(. ), – and all sufficiently large n’s Prob[Bob moves Y | Alice does not approve] ≤ 1/p(n) • Recall observation: what Bob and Charlie received in the setup phase might as well be public • Claim: can get rid of interaction: – given an interactive identification protocol possible to construct a noninteractive one. In the new protocol: • Alice` sends Bob` the random bits Alice used to generate the setup information • Bob` simulates the conversation between Alice and Bob in original protocol and accepts only if simulated Bob accepts. • Probability of cheating is the same

One-way functions are essential to the two guards password problem • Are we done? Given a noninteracive identification protocol want to define a one-way function • Define f(r): the setup phase mapping between the random bits r of Alice and the information y given to Bob and Charlie • Problem: the function f(r) is not necessarily oneway… – Can be unlikely ways to generate it. Can be exploited to invert. – Example: Alice chooses x, x’ {0, 1}n if x’= 0 n set y=x o. w. set y=f(x) – The protocol is still secure, but with probability 1/2 n not

One-way functions are essential to the two guards password problem… • However: possible to estimate the probability that Bob accepts on a given string from Alice • Second attempt: define function f(r) as – the mapping that Alice does in the setup phase between her random bits r and the information given to Bob and Charlie, – plus a bit indicating that probability of Bob accepts given r is greater than 2/3 Theorem: the two guards password problem has a solution if and only if one-way functions exist

Examples of One-way functions Examples of hard problems: • Subset sum • Discrete log • Factoring (numbers, polynomials) into prime components Easy problem How do we get a one-way function out of them?

Weak One-way function A function f: {0, 1}n → {0, 1}n is called a weak oneway function, if • f is a polynomial-time computable function • There exists a polynomial p(¢), for every probabilistic polynomial-time algorithm A, and all sufficiently large n’s Prob[A[f(x)] f-1(f(x)) ] ≤ 1 -1/p(n) Where x is chosen uniformly in {0, 1}n and the probability is also over the internal coin flips of A
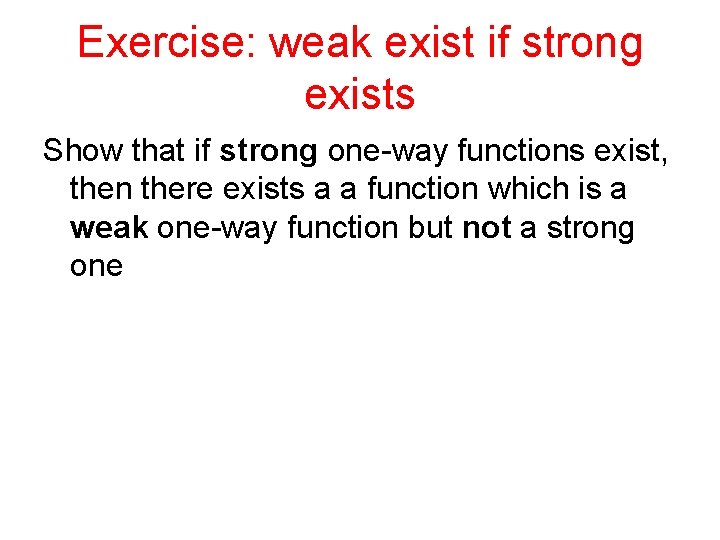
Exercise: weak exist if strong exists Show that if strong one-way functions exist, then there exists a a function which is a weak one-way function but not a strong one

What about the other direction? • Given – a function f that is guaranteed to be a weak one-way • Let p(n) be such that Prob[A[f(x)] f-1(f(x)) ] ≤ 1 -1/p(n) – can we construct a function g that is (strong) oneway? An instance of a hardness amplification problem • Simple idea: repetition. For some polynomial q(n) define g(x 1, x 2 , …, xq(n) )=f(x 1), f(x 2), …, f(xq(n)) • To invert g need to succeed in inverting f in all q(n) places – If q(n) = p 2(n) seems unlikely (1 -1/p(n))p 2(n) ≈ e-p(n) – But how to we show? Sequential repetition intuition –

Want: Inverting g with low probability implies inverting f with high probability • Given a machine A that inverts g want a machine A’ – operating in similar time bounds – inverts f with high probability • Idea: given y=f(x) plug it in some place in g and generate the rest of the locations at random z=(y, f(x 2), …, f(xq(n))) • Ask machine A to invert g at point z • Probability of success should be at least (exactly) A’s Probability of inverting g at a random point • Once is not enough • How to amplify? – Repeat while keeping y fixed – Put y at random position (or sort the inputs to g )

Proof of Amplification for Repetition of Two • Concentrate on repetition of two g(x 1, x 2 )=f(x 1), f(x 2) • Goal: show that the probability of inverting g is roughly squared the probability of inverting f just as would be sequentially • Claim: Let (n) be a function that for some p(n) satisfies 1/p(n) ≤ 1 -1/p(n) Let ε(n) be any inverse polynomial function suppose that for every polynomial time A and sufficiently large n Prob[A[f(x)] f-1(f(x)) ] ≤ (n) Then for every polynomial time B and sufficiently large n Prob[B[g(x , x )] g-1(g(x , x )) ] ≤ 2(n) + ε(n)

Proof of Amplification for Two Repetition Suppose not, then given a better than 2+ε algorithm B for inverting g construct the following: • B’(y) Inversion algorithm for f – Repeat t times • • Choose x’ at random and compute y’=f(x’) Helpful for Run B(y, y’). constructive Check the results algorithm If correct: Halt with success – Output failure Inner loop
![Probability of Success Define Syfx ProbInner loop successful y β Probability of Success • Define S={y=f(x) | Prob[Inner loop successful| y ] > β}](https://slidetodoc.com/presentation_image/e9b6aa89e8b2ec2a153b90c30c42cf5b/image-47.jpg)
Probability of Success • Define S={y=f(x) | Prob[Inner loop successful| y ] > β} • Since the choices of the x’ are independent Prob[B’ succeeds| x S] > 1 -(1 - β)t Taking t= n/β means that when y S almost surely A will invert it • Hence want to show that Prob[ y S] > (n)

The success of B • Fix the random bits of B. Define P={(y 1, y 2)| B succeeds on (y 1, y 2)} P= P ⋂ {(y 1, y 2 )| y 1, y 2 S} ⋃ P ⋂ {(y 1, y 2 )| y 1 S} y 1 ⋃ P ⋂ {(y 1, y 2 )| y 2 S} Well behaved part y 2 P want to bound P by a square
![S is the only success But ProbBy 1 y 2 g1y 1 y S is the only success. . But Prob[B[y 1, y 2] g-1(y 1, y](https://slidetodoc.com/presentation_image/e9b6aa89e8b2ec2a153b90c30c42cf5b/image-49.jpg)
S is the only success. . But Prob[B[y 1, y 2] g-1(y 1, y 2) | y 1 S] ≤ β and similarly Prob[B[y 1, y 2] g-1(y 1, y 2) | y 2 S] ≤ β so Prob[(y 1, y 2) P and y 1, y 2 S] ≥ Prob[(y 1, y 2) P ] - 2β ≥ 2+ ε - 2β Setting β =ε/3 we have Prob[(y 1, y 2) P and y 1, y 2 S] ≥ 2+ ε/3
![Contradiction But Proby 1 y 2 P and y 1 y 2 S Contradiction But Prob[(y 1, y 2) P and y 1, y 2 S] ≤](https://slidetodoc.com/presentation_image/e9b6aa89e8b2ec2a153b90c30c42cf5b/image-50.jpg)
Contradiction But Prob[(y 1, y 2) P and y 1, y 2 S] ≤ Prob[y 1 S] Prob[y 2 S] = Prob 2[y S] So Prob[y S] ≥ √(α 2+ ε/3) > α

Is there an ultimate one-way function? Aka * and`universal’ • If f 1: {0, 1}* → {0, 1} f 2: {0, 1}* → {0, 1}* are guaranteed to: – Be polynomial time computable – At least one of them is one-way. then can construct a function g: {0, 1}* → {0, 1}*Robust which is Combiner one-way: g(x 1, x 2 )= (f 1(x 1), f 2 (x 2 )) • If an 5 n 2 time one-way function is guaranteed to exist, can construct an O(n 2 log n) one-way function g: – Idea: enumerate Turing Machine and make sure they run 5 n 2 steps g(x 1, x 2 , …, xlog (n) )=M 1(x 1), M 2(x 2), …, Mlog n(xlog (n)) • If a one-way function is guaranteed to exist, then there 1/p(n) exists a 5 n 2 time one-way:

Ultimate one-way function conclusions Original proof due to L. Levin • Be careful what you wish for • Problem with resulting one-way function: – Cannot learn about behavior on large inputs from small inputs – Whole rational of considering asymptotic results is eroded • Construction does not work for non-uniform oneway functions • Notion of robust combiner seems fundamental – See “Robust Combiners for Oblivious Transfer and Other Primitives” by Harnik, Kilian, Naor , Reingold and Rosen, Eurocrypt 2005

On One-Way Functions • A function f is one-way if: – it is computable in poly-time – the probability of successfully finding an inverse in poly-time is negligible (on a random input) • A function f is distributionally one-way if: – it is computable in poly-time – No poly-time algorithm can successfully find a random inverse (on a random input) Theorem [Impagliazzo Luby 89]: distributionally one-way functions exist iff one-way functions exists

Distributionally one-way functions • Definition: function f: {0, 1}* is distributionally one-way if – for some constant c>0 for every pptm M the distributions: – x◦f(x) – M(f(x))◦f(x) Are statistically distinguishable by a least n-c

Existence of distributionally oneway functions Theorem: distributionally one-way functions exist iff one-way functions exists Proof: Suppose f be a distributionally one-way function with constant c Construct a weak one-way function g Need H - a family of pairwise independent functions Let g(x, h, i) = hf(x), h, i, prefi(h(x))i Guess of (log) the number of pre-images Claim, if f be a distributionally one-way function, then g is a weak one-way function

Application: bit commitment • Sender - Input b {0, 1} Receiver • Two Phases – Commit – Reveal • At the end of protocol: Receiver obtains b decides valid or not

Commitment Protocol Commit Phase Sender b Receiver Sender is bound to b Reveal Phase Sender b Receiver can verify b was the value in the box

Following Commit Phase • Receiver should not have gained any information about b – Information theoretic? – Computationally? • Sender should be bound to b – No two different and valid openings exist – It is computationally infeasible to find two different valid openings

Both worlds? Cannot have best of both worlds: • Information theoretic secrecy following commit – Distribution of conversation independent of b • Perfect binding – No two different and valid openings exist whp

One-way functions are essential for bitcommitment Protocol may be interactive Let f(b, r. A, r. B) be the transcript of the commit phase with – sender having input b and random string r. A – receiver having input b and random string r. B • Claim: f is a distributionally one-way function – Suppose not, then given a typical transcript c=f(b, r. A, r. B ) • Can find random inverses in f-1(c) • Run an find a small collection of invreses in f-1(c) – Two possibilities: Make sure that the receiver accepts the value when inputs are string are b, r. A and r. B • Most of the inverses have the same value b – Can break the secrecy • Different values of b occur

Existence of one-way functions is equivalent: The existence of one-way functions is equivalent to • Pseudo-random generators [HILL] • Pseudo-random functions and permutations – Block ciphers • Bit commitment – ~ zero-knowledge • Signature Schemes • (Non trivial) shared-key encryption Goal of these talk: add two other items to the list: • Sub-linear authentication • Memory Checking

References Books: • O. Goldreich, Foundations of Cryptography a book in three volumes. – Vol 1, Basic Tools, Cambridge, 2001 • One-way Functions, Pseudo-randomness, zero-knowledge – See other volumes in www. wisdom. weizmann. ac. il/~oded/books. html • R. Impagliazzo and M. Luby, One-way Functions are Essential for Complexity Based Cryptography, FOCS 1989:
 Necessary and sufficient conditions examples
Necessary and sufficient conditions examples Necessary and sufficient conditions examples
Necessary and sufficient conditions examples Necessary and sufficient conditions examples
Necessary and sufficient conditions examples Example of necessary cause
Example of necessary cause Best worst and average case
Best worst and average case Blackcipher bypass
Blackcipher bypass Lcs35
Lcs35 Symmetric key distribution using asymmetric encryption
Symmetric key distribution using asymmetric encryption Two simple hash functions
Two simple hash functions Www owasp org
Www owasp org Cryptographic concepts
Cryptographic concepts Pin punctures steganography
Pin punctures steganography Cryptographic tools
Cryptographic tools Cryptographic
Cryptographic Cryptographic
Cryptographic Network security essentials 5th edition
Network security essentials 5th edition Cryptographic attacks
Cryptographic attacks Owasp top ten most critical web application vulnerabilities
Owasp top ten most critical web application vulnerabilities Simple key loader
Simple key loader Insecure cryptographic storage challenge 3
Insecure cryptographic storage challenge 3 Sadlier vocabulary workshop level d unit 12
Sadlier vocabulary workshop level d unit 12 Haqooq ul allah
Haqooq ul allah A single countermeasure is sufficient for sqli attacks
A single countermeasure is sufficient for sqli attacks Sufficient recurve
Sufficient recurve My grace is sufficient for you
My grace is sufficient for you Sufficient statistics
Sufficient statistics Dionysian vs apollonian
Dionysian vs apollonian Simply sufficient
Simply sufficient Long case vs short case
Long case vs short case Binary search algorithm average complexity
Binary search algorithm average complexity Bubble sort best case and worst case
Bubble sort best case and worst case Bubble sort best case and worst case
Bubble sort best case and worst case Bubble sort best case and worst case
Bubble sort best case and worst case Ambiguous case trigonometry
Ambiguous case trigonometry Inherent powers examples
Inherent powers examples Expressed powers cartoon
Expressed powers cartoon Necessary life functions and survival needs
Necessary life functions and survival needs Why fiber joints and couplers are necessary?
Why fiber joints and couplers are necessary? Necessary life functions anatomy and physiology
Necessary life functions anatomy and physiology Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Slidetodoc
Slidetodoc Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Gấu đi như thế nào
Gấu đi như thế nào Chụp phim tư thế worms-breton
Chụp phim tư thế worms-breton Bài hát chúa yêu trần thế alleluia
Bài hát chúa yêu trần thế alleluia Môn thể thao bắt đầu bằng từ đua
Môn thể thao bắt đầu bằng từ đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính thế năng
Công thức tính thế năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân Làm thế nào để 102-1=99
Làm thế nào để 102-1=99 Phản ứng thế ankan
Phản ứng thế ankan Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng nó xinh thế
Cái miệng nó xinh thế Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Ví dụ về giọng cùng tên
Ví dụ về giọng cùng tên