On Matrix Painleve Systems Yoshihiro Murata Nagasaki University

On Matrix Painleve Systems Yoshihiro Murata Nagasaki University 20 September 2006 Isaac Newton Institute 　

Contents 1. Introduction 2. Dimensional Reductions of ASDYM eqns and Matrix Painleve Systems (Reconstruction of the result of Mason & Woodhouse) 3. Degenerations of Painleve Equations and Classification of Painleve Equations 4. Generalized Confluent Hypergeometric Systems included in MPS (joint work with Woodhouse) 2

1. Introduction Basic Motivation Can we have new good expressions of Painleve eqns to achieve further developments? (Background) We often use various expressions to find features of Painleve: e. g. Painleve systems (Hamiltonian systems) 3 -systems of order 1 (Noumi-Yamada system) Answer: New possively good expressions exist. 3

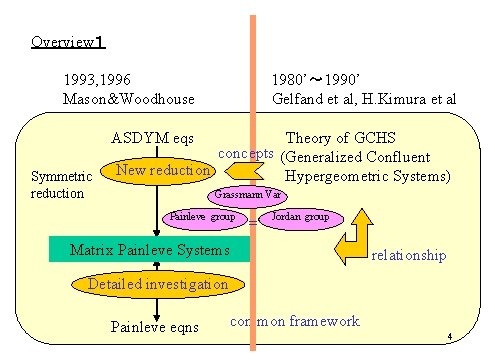
Overview１ 1993, 1996 Mason&Woodhouse 1980’～ 1990’ Gelfand et al, H. Kimura et al ASDYM eqs Symmetric reduction Theory of GCHS concepts (Generalized Confluent New reduction Hypergeometric Systems) Grassmann Var Painleve group = Jordan group Matrix Painleve Systems reduced eqs (Matrix ODEs) 　relationship Detailed investigation Painleve eqns common framework 4

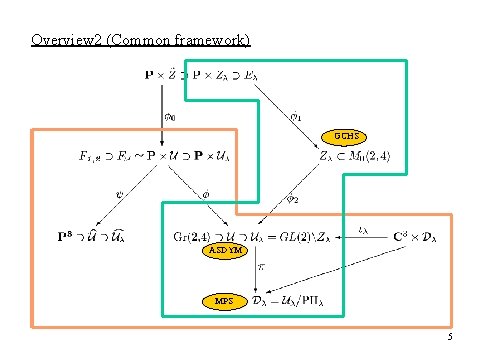
Overview 2 (Common framework) GCHS ASDYM MPS 5

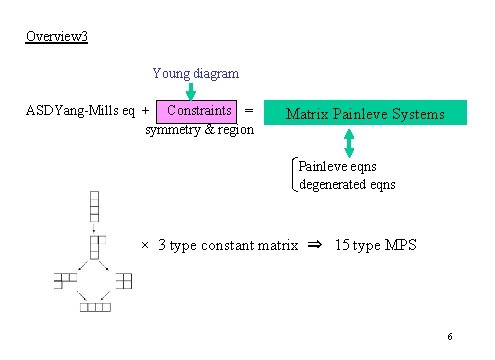
Overview 3 Young diagram ASDYang-Mills eq + Constraints = symmetry & region Matrix Painleve Systems Painleve eqns degenerated eqns × 3 type constant matrix ⇒　15 type MPS 6

2. Dimmensional Reductions of ASDYM eqns and Matrix Painleve Systems 2. 1 Preliminaries Painleve III’　 Third Painleve eqn has two expressions: These are transformed by PIII’ is often better than PIII 7

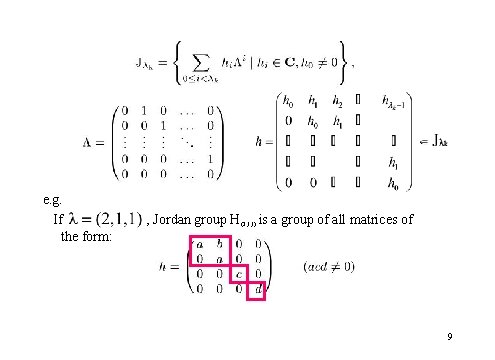
Young diagrams and Jordan groups (Basic concepts in theory of GCHS) We express a Young diagram by the symbol λ If λ consists l rows and write as e. g. For Hλ　as follows: boxes, we define Jordan group 8

e. g. If the form: , Jordan group H(2, 1, 1) is a group of all matrices of 9

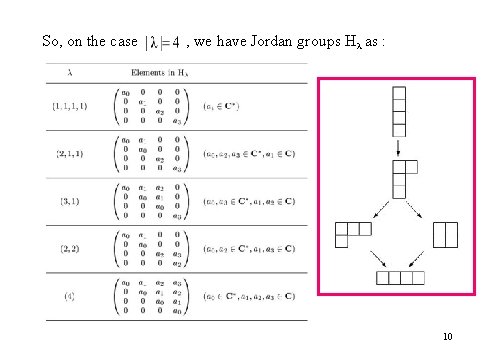
So, on the case , we have Jordan groups Hλ as : 10

Subdiagrams and Generic stratum of M(r, n) (Basic concepts in theory of GCHS) e. g. If , then subdiagrams μof weight 2 are (2, 0, 0), (1, 1, 0), (1, 0, 1), (0, 1, 1) 11

e. g. On the case M(2, 4), λ = (2, 1, 1), μ= (1, 0, 1)　 e. g. 12

2. 2 New Reduction Process We consider the ASDYM eq defined on a Grassmann variety. Reduction Process (1) Take where Let then (2) Take a metric Let sl(2, C) gauge potential satisfies ASD condition on 13

ASDYM eqn (3) We consider projective Jordan group whereλare Young diagrams of weight 4. PHλacts (4) Restrict ASDYM onto PHλinvarinat regions 14

(5) Let . Then gives 3 -dimensional fibration 15

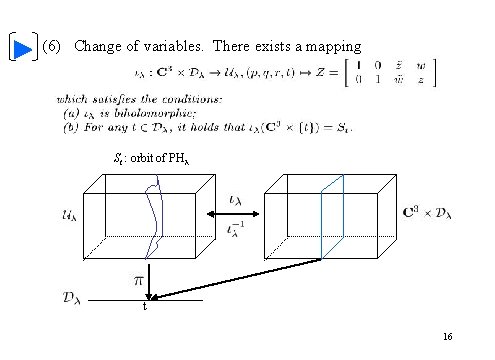
(6) Change of variables. There exists a mapping St : orbit of PHλ t 16

(7) PHλ–invariant ASDYM eqn Lλ (8) Calculations of three first integrals 17

2. 3 Matrix Painleve Systems We call the combined system (Lλ＋1 st Int) Matrix Painleve Sytem Mλ 18

We obtained 5 types of Matrix Painleve Systems: By gage transformations, constant matrix P is classified into 3 cases: Thoerem 1 By the reduction process (1), …, (8), we can obtain Matrix Painleve Systems Mλfrom ASDYM eqns. Mλare classified into 15 cases by Young diagram λand constant matrix P. A B C 19

3. Degenerations of Painleve Equations 4. and Classification of Painleve Equations 3. 1 Degenerations and Classification of Painleve eqns e. g. 　　　　　 PVI　 PV PIII’ PII PI　　　　　 20

PV is divided into two different classes: PV(δ≠ 0) PV(δ＝ 0) can be transformed into Hamiltonian system SV can’t use SV； and equivalent to PIII’(γδ≠ 0) PIII’ is divided into four different classes: (by Ohyama-Kawamuko-Sakai-Okamoto) PIII’(γδ≠ 0) type D 6 generic case of PIII’ can be transformed into Hamiltonian sytem SIII’ PIII’(γ＝ 0, αδ≠ 0) type D 7 PIII’(γ＝ 0, δ=0, αβ≠ 0) type D 8 PIII’(β＝δ＝ 0) type Q solvable by quadrature PI : If we change eq to , it is solvable by Weierstrass 21

For special values of parameters, PJ (J=II…VI) have classical solutions. Equations which have classical sol can be regarded as degenerated ones. This type degeneration is related to transformation groups of solutions. Question 1: Can we systematically explain these degenerations? Question 2: Can we classify Painleve eqns by intrinsic reason? 22

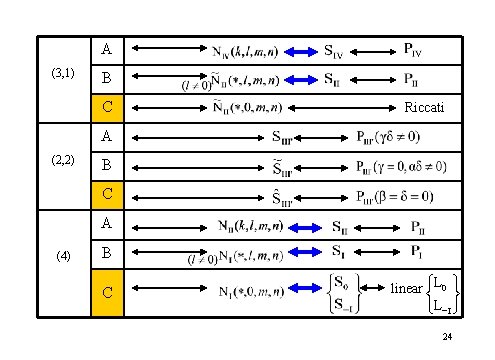
3. 2 Correspondences between Matrix Painleve Systems and Painleve Equations Theorem 2 λ (1, 1, 1, 1) P A Correspondences B C A (2, 1, 1) B C 　　　　 under calculation 23

A (3, 1) B C Riccati A (2, 2) B C A (4) B C L 0 ü linear ì í ý î L- I þ 24

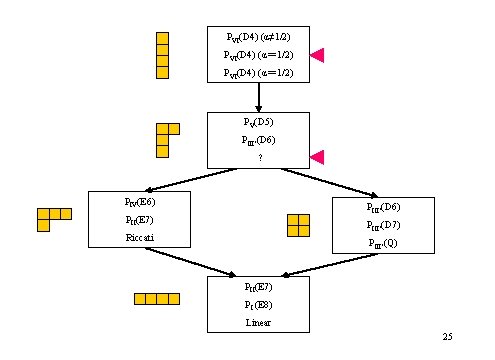
PVI(D 4) (α≠ 1/2) PVI(D 4) (α＝ 1/2) PV(D 5) PIII’(D 6) ? PIV(E 6) PIII’(D 6) PII(E 7) PIII’(D 7) Riccati PIII’(Q) PII(E 7) PI (E 8) Linear 25

(1) Nondeg cases of MPS correspond to PII, …, PVI. (2) All cases of Painleve eqns are written by Hamiltonian systems. (3) Degenerations of Painleve eqns are characterized by Young diagramλand constant matrix P. Degenerations of Painleve eqn are classified into 3 levels: 1 st level: depend on λonly 　　　2 nd level: depend on λand P 3 rd level: depend on transformation group of sols (4) Parameters of Painleve Systems are rational functions of parameters (k, )l, m, n. (5) On , numbers of parameters are decreased at the steps of canonical transformations between NJ and SJ. 26

4. Generalized Confluent Hypergeometric Systems included in MPS (joint work with Woodhouse) Summary 1 (general case) Theory of GCHS is a general theory to extend classical hypergeometric and confluent hypergeometric systems to any dimension paying attention to symmetry of variables and algebraic structure. Original GCHS is defined on the space. Factoring out the effect of the group , , we obtain GCHS on and GCHS on Concrete formula of is obtained (with Woodhouse) 27

Summary 2 (On the case of MPS) Painleve System SJ (J=II～VI) contains Riccati eqn RJ. RJ is transformed to linear 2 -system LSλ contained in Mλ(k, l, m, n). LSλhas 3 -parameters. Let denote lifted up systems of onto , then we have following diagram. (1, 1, 1, 1) Gauss Hypergeometric (2, 1, 1) Kummer (3, 1) Hermite (2, 2) Bessel (4) Airy 28

From these, Matrix Painleve Systems may be good expressions of Painleve eqns. 29

References: H. Kimura, Y. Haraoka and K. Takano, The Generalized Confluent Hypergeometric Functions, Proc. Japan Acad. , 69, Ser. A (1992) 290 -295. Mason and Woodhouse, Integrability Self-Duality, and Twistor Theory, London Mathematical Society Monographs New Series 15, Oxford University Press, Oxford (1996). Y. Murata, Painleve systems reduced from Anti-Self-Dual Yang-Mills equation, DISCUSSION PAPER SERIES No. 2002 -05, Faculty of Economics, Nagasaki University. Y. Murata, Matrix Painleve Systems and Degenerations of Painleve Equations, in preparation. Y. Murata and N. M. J. Woodhouse, Generalized Confluent Hypergeometric Systems on Grassmann Variety, DISCUSSION PAPER SERIES No. 2005 -10, Faculty of Economics, Nagasaki University. Y. Murata and N. M. J. Woodhouse, Generalized Confluent Hypergeometric Systems included in Matrix Painleve Systems, in preparation. 30