On Diffusion Processes Lvy Noises and Confusion Ccile

On Diffusion Processes, Lévy Noises, and Confusion Cécile Penland NOAA/Earth Systems Research Laboratory

How do we model unresolved variability? • Diffusion approximation? • Lévy-driven processes? Better representation of tails? • Does our experience with diffusion processes transfer to (white) Lévy-driven processes?

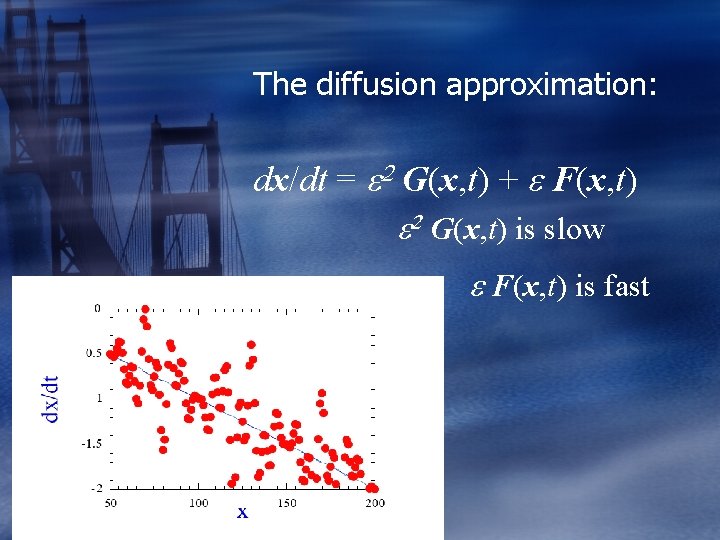
The diffusion approximation: dx/dt = e 2 G(x, t) + e F(x, t) e 2 G(x, t) is slow e F(x, t) is fast

Choose a scaling s = e 2 t: . (*) For simplicity, say and Lim (*) -> t->∞ e->0 (W is a Brownian motion; d. W N( , dt)).

The Good: • Have a systematic way of handling a lot of multiscale processes. • Rigorous connection between dynamics (PDEs) and probabilistic description. implies a Stratonovich Fokker-Planck eqn.

The Bad: • Existence of multiple calculi can make numerical generation difficult. • The difference between Ito and Stratonovich integrals is physically-based; a thermometer will not perform the Ito correction for you. • Mathematically, it’s an issue of who speaks first: the continuum limit or the white-noise limit.

NWS operational GCM (1993 version)

The Bad: • Existence of multiple calculi can make numerical generation difficult. • The difference between Ito and Stratonovich integrals is physically-based; a thermometer will not perform the Ito correction for you. • Mathematically, it’s an issue of who speaks first: the continuum limit or the white-noise limit.

The Ugly: • Sometimes, the approximation just doesn’t hold. • The white-noise limit and Gaussian limit in the CLT are more or less taken simultaneously when that doesn’t always happen in nature.

The new fashion: Lévy noises P(X>x) ~ x- xs for s> Also get Langevin equations: d. X = f(X)dt+ (X) d. L

Why do we care? w Anomalous diffusion in hydrology (Hurst 1951) w Paleoclimate models, particularly as concerns intermittency in the ice core record (e. g. , Ditlevsen 1999) w Atmospheric turbulence (Viecelli 1998) Even if we object to some of these models, we still have to know how to analyze them.

w d. X = f(X)dt+ (X) d. L Fractional Fokker-Planck equation is derived in spectral form as the continuum limit of a finite jump process.

Questions for the Mathematicians w Theoretical justification w Implementation

w When can we get away with treating a Lévy process as a system driven by multiplicative Brownian noise? w Are there limit theorems for continuous systems which converge to continuous Lévy-driven processes? w If there are limit theorems converging to Lévydriven processes, what are the requirements for convergence? w How forgiving are these limit theorems?

w Do Lévy processes ever approximate the physical system when the white-noise limit is pretty good but the Gaussian limit is not? Under what circumstances? w Are there classes of Lévy noises for which the stochastic integral is not unique? w If so, what does the Lévy equivalent of a noiseinduced drift look like? Does it involve a fractional derivative? Are there transformations between calculi?

w Are there really limit theorems that would give combinations of Lévy and Brownian noises in the same dynamical equation? w Is there a recipe like the CLT that scientists can use to get an approximate stochastic equation? w Is there such a thing as a Lévy-Taylor expansion?

Choose a scaling s = e 2 t: . (*) For simplicity, say and Lim (*) -> t->∞ e->0 (W is a Brownian motion; d. W N( , dt)).

w Are there limit theorems that would give combinations of Lévy and Brownian noises in the same dynamical equation? w Is there a recipe like the CLT that scientists can use to get an approximate stochastic equation? w Is there such a thing as a Lévy-Taylor expansion?

w Is there such a thing as an Ito-Lévy-Taylor expansion? w What about the numerical generation of Lévy noises? Do we use ( )1/ R to update the noisy increment? w Since some models use combinations of Wiener and Lévy noises, can we use the same numerical scheme to update both terms?

w How do we handle multiple stochastic integrals when some of the noises are Brownian and others are Lévy? w If we only care about the distribution of the solution, are there weak and strong numerical schemes for Lévy-driven processes like there are for Wiener-driven processes? w Does the accuracy of these schemes depend on any particular calculus like it does for Wienerdriven schemes?

w. What else is out there?