On Balanced Signed Graphs and Consistent Marked Graphs

On Balanced Signed Graphs and Consistent Marked Graphs Fred S. Roberts DIMACS, Rutgers University Piscataway, NJ, USA

Signed Graphs and Marked Graphs Data in the social sciences can often be modeled using a signed graph: A graph where every edge has a sign + or –. Less widely used in the social sciences is a marked graph, where every vertex has a sign + or –. A signed graph is balanced if every cycle has an even number of – signs. A marked graph is consistent if every cycle has an even number of – signs.

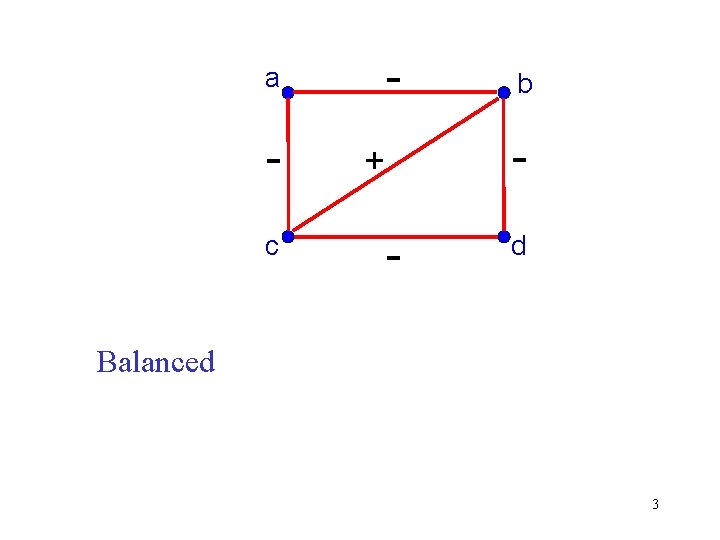
- a c + - b d Balanced 3

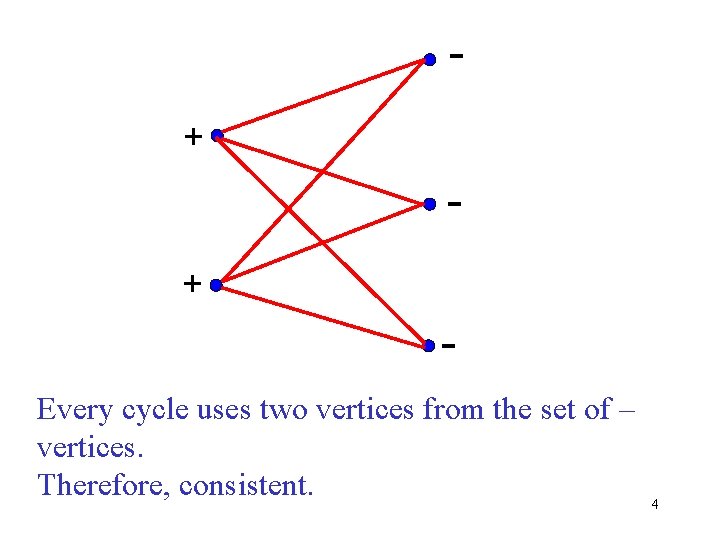
+ + Every cycle uses two vertices from the set of – vertices. Therefore, consistent. 4

We will speak of the sign of a path or cycle as being + if it has an even number of – signs, and – otherwise. So: a signed graph is balanced iff every cycle is +. A marked graph is consistent iff every cycle is +. 5

Balance: Sociological Motivation Small group is “balanced” if it works well together, lacks tension. Signed graphs used to “explicate” this concept. Vertices = people Edges = strong relationship Sign = positive or negative (likes/dislikes, lies/tells truth to, associates with/avoids) 6

Balance: Sociological Motivation Balanced signed graphs introduced as model for balanced small groups by Cartwright and Harary in early 1950 s. Evidence that small group is balanced iff its corresponding signed graph is balanced. 7

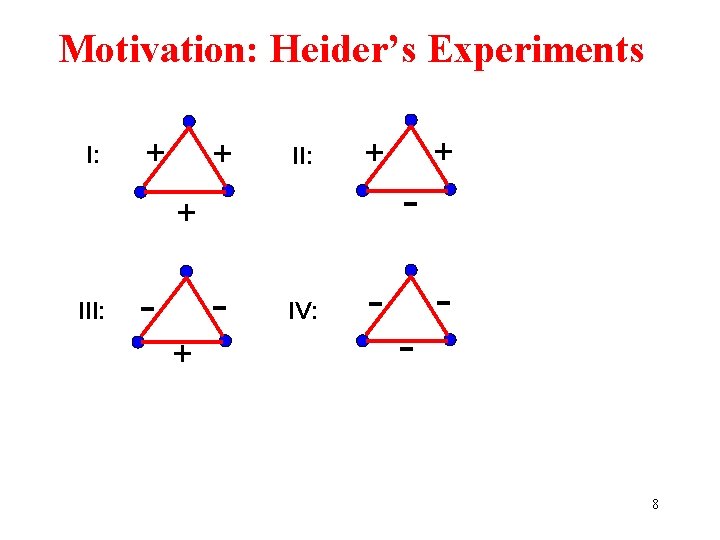
Motivation: Heider’s Experiments I: + + II: - IV: - + III: + + + - - - 8

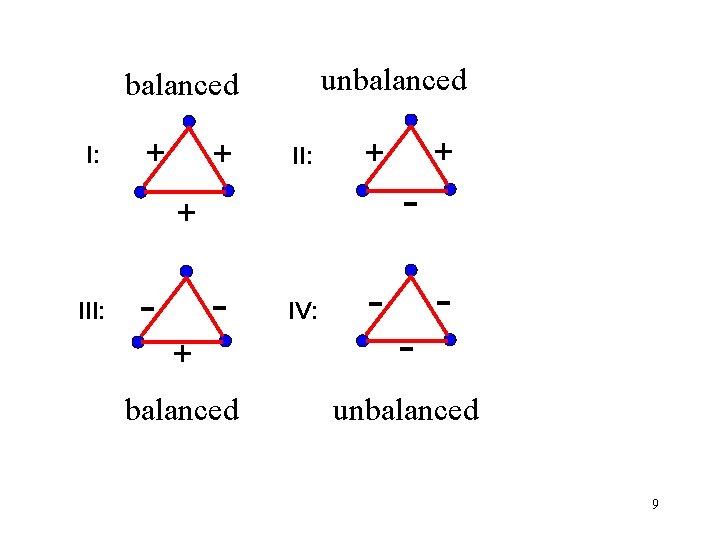
unbalanced I: + + II: - IV: - + III: - + + - - + - balanced unbalanced 9

Balance: Other Applications Political science: international relations Vertices = countries, signs = allies/enemies Analysis of literature: At point of “tension, ” tension is resolved by changing to balance. 10

Balance: Other Applications Sociology: social justice, analysis of inequities. Economics: Analysis of structure of mathematical models for large complex systems such as those used to analyze energy and economic systems 11

Characterization of Balanced Signed Graphs Theorem (Harary 1954): A signed graph G is balanced iff the set of vertices of G can be partitioned into two disjoint sets such that each + edge joins vertices in the same set and each – edge joins vertices in different sets. 12

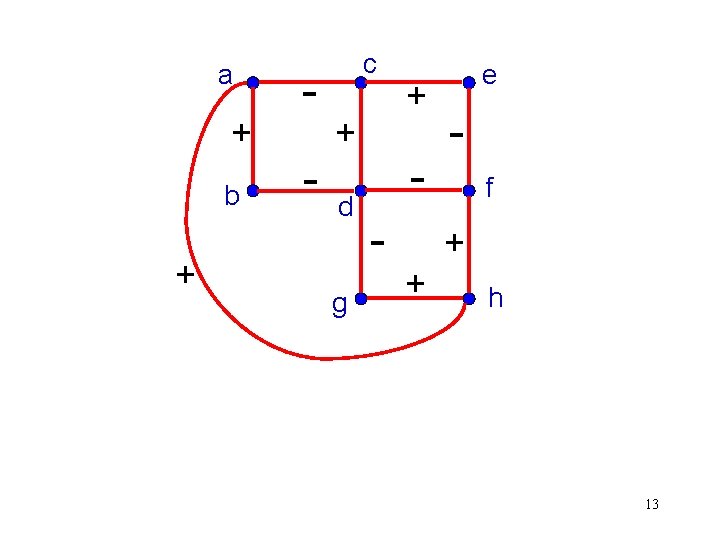
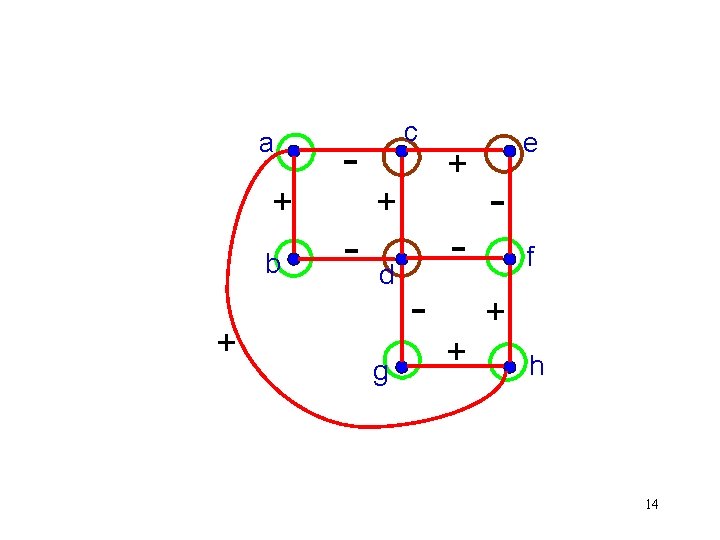
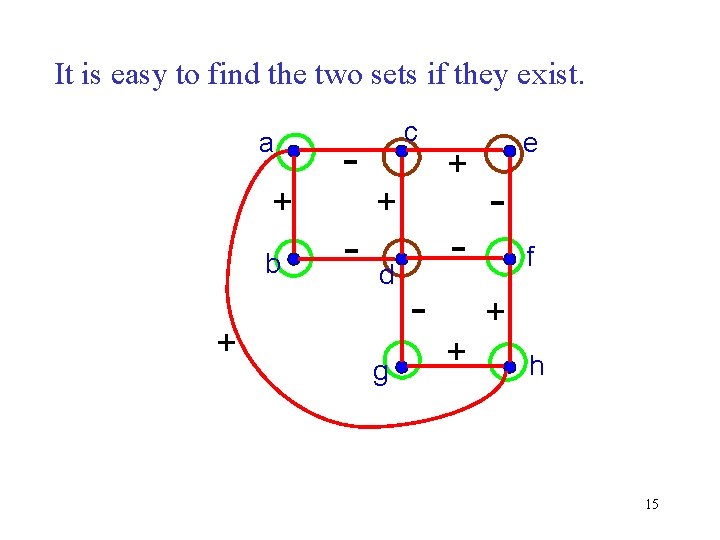
It is easy to find the two sets if they exist. a + b + - c + d g + - e f + + h 15

This can be made into a linear time algorithm to check for balance (Maybee and Maybee 1983, Hansen 1978). 16

Idealized Political Party Structure Idealized party structure: Whenever members of the same party have a dialogue, they agree; whenever members of different parties have a dialogue, they disagree. 17

Idealized Political Party Structure Idealized party structure: Whenever members of the same party have a dialogue, they agree; whenever members of different parties have a dialogue, they disagree. Theorem: A political system is balanced iff it has an idealized two party structure. 18

Idealized Political Party Structure Idealized party structure: Whenever members of the same party have a dialogue, they agree; whenever members of different parties have a dialogue, they disagree. Theorem: A political system is balanced iff it has an idealized two party structure. One party could be empty. 19

Balance and Graph Coloring Balanced signed graphs are a generalization of bipartite graphs or 2 -colorable graphs. (Given undirected graph, let all signs be –. ) There is (as in political party example) also interest in finding ways to partition the vertices of a signed graph into more than two sets (more than two colors) so that all + edges join vertices of the same set and all – edges join vertices of different sets. 20 So, balance theory is a type of coloring theory.

Testing the Balance Model How does one test the model? Morisette’s experiments. 21

Consistent Marked Graphs: Communication Networks Motivation Binary messages sent through a network. Messages reversed at – vertices. In a consistent marked graph: If a message is sent from x to y through two different vertex-disjoint paths and x and y have the same sign, then y will receive the same message no matter which path is followed. 22

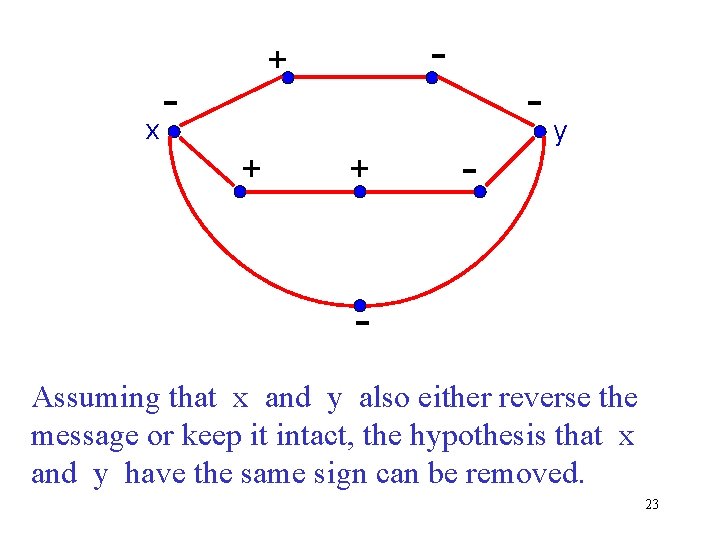
- + x + + - y Assuming that x and y also either reverse the message or keep it intact, the hypothesis that x and y have the same sign can be removed. 23

Consistent Marked Graphs Social Networks Interpretation: Vertices represent people who always lie or always tell the truth. Characterization Problem: There is no simple structural characterization of consistent marked graphs analogous to the 2 -class structural theorem for balance. 24

Main Agenda of this Talk 1. Results about graphs that have consistent markings 2. Efficient Algorithms for determining if a marked graph has a consistent marking 3. The “markability problem”: When can we mark a graph with signs on vertices (at least one –) to obtain consistency? 25

Connection Among Balance, Consistency, and other Graphtheoretical Notions: Balance and Consistency Signed graph G. Put a + sign on each vertex and insert a vertex with – sign in each negative edge. Get a marked graph H. G is balanced iff H is consistent. 26

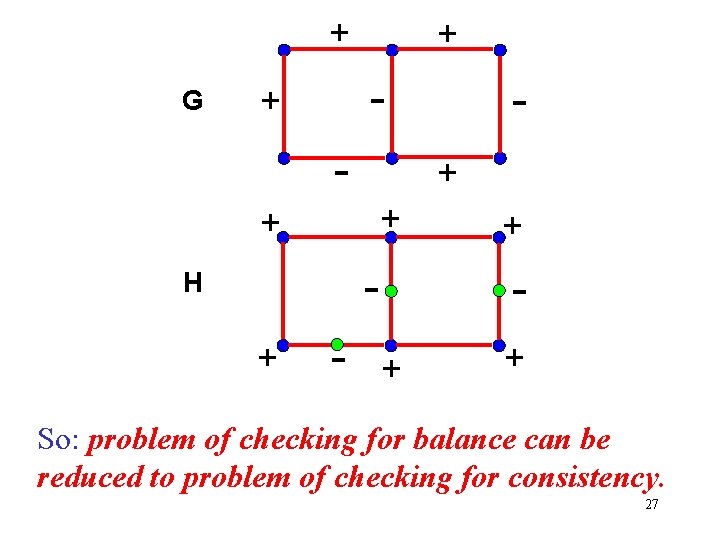
+ G + - + + + - H + - + + + So: problem of checking for balance can be reduced to problem of checking for consistency. 27

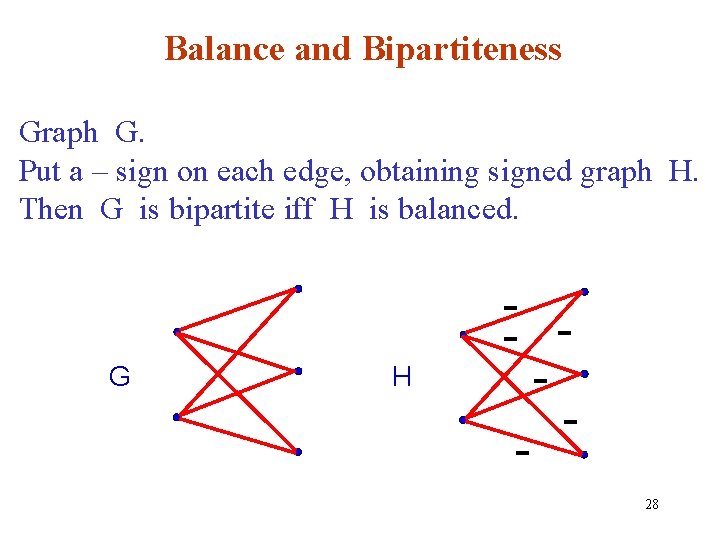
Balance and Bipartiteness Graph G. Put a – sign on each edge, obtaining signed graph H. Then G is bipartite iff H is balanced. G H - 28

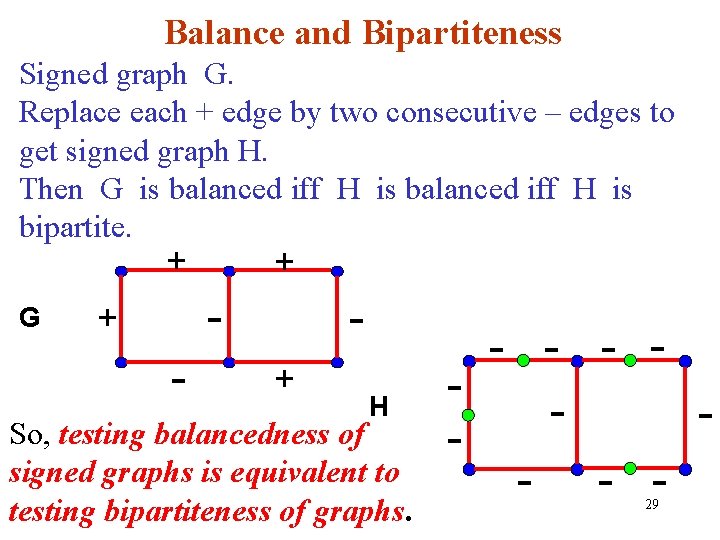
Balance and Bipartiteness Signed graph G. Replace each + edge by two consecutive – edges to get signed graph H. Then G is balanced iff H is bipartite. + G + - + H So, testing balancedness of signed graphs is equivalent to testing bipartiteness of graphs. - - - 29

Double Balancedness Bipartite graph G. If each cycle has length 0 mod 4, say G is double balanced. Bipartite graph G. Assign + signs to one bipartite class and – signs to the other, getting marked graph H. Then, G is double balanced iff H is consistent. 30

Double Balancedness Marked graph G. Insert a + vertex in each edge incident to 2 – vertices and insert 3 vertices with signs –, +, – in each edge incident to 2 + vertices, getting marked graph H. Then H is bipartite with one part + and the other part –. Moreover, G is consistent iff H is double balanced. Proof is by induction on number of edges of G that join vertices of the same sign. 31

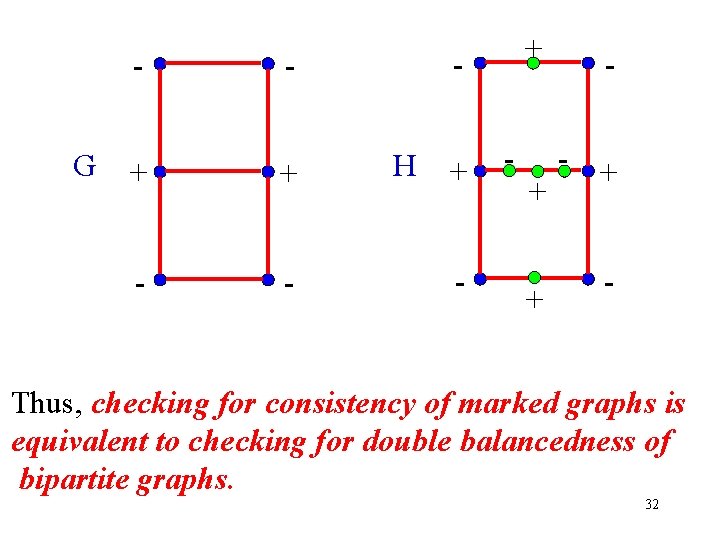
G - - + + - - + H + - - + + - Thus, checking for consistency of marked graphs is equivalent to checking for double balancedness of bipartite graphs. 32

Characterization of Consistency I G[V+] = subgraph induced by all + vertices G[V–] = subgraph induced by all – vertices. Theorem (Acharya 1984, Rao 1984). If marked graph G is consistent, then G[V–] is bipartite. Moreover, there is at most one edge between each component of G[V+] and each set in the bipartition of each component of G[V–]. 33

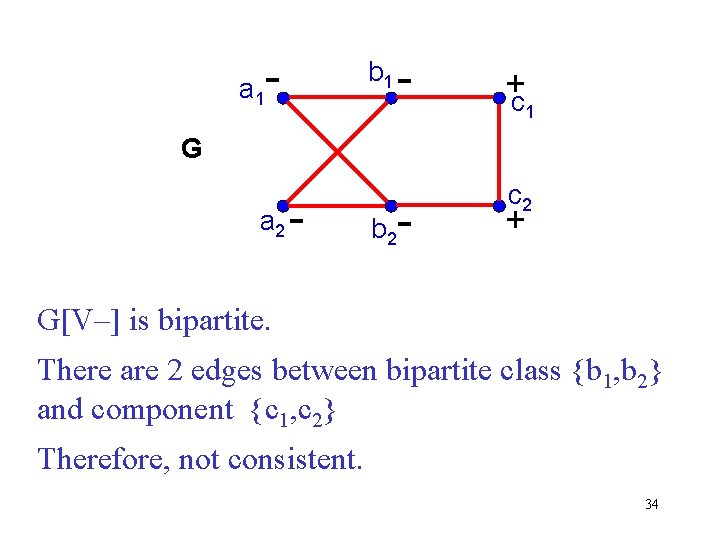
a- b 1 1 - +c - c 2 1 G a 2 - b 2 + G[V–] is bipartite. There are 2 edges between bipartite class {b 1, b 2} and component {c 1, c 2} Therefore, not consistent. 34

Characterization of Consistency I Theorem (R and Xu 2003). Let G be a 2 connected marked graph satisfying the necessary conditions of the Theorem of Acharya and Rao. Shrink each component of G[V–] that is not a single vertex into a single edge, to get marked graph H. Then G is consistent iff H is. This is sometimes helpful in reducing size of graphs in checking for consistency. 35

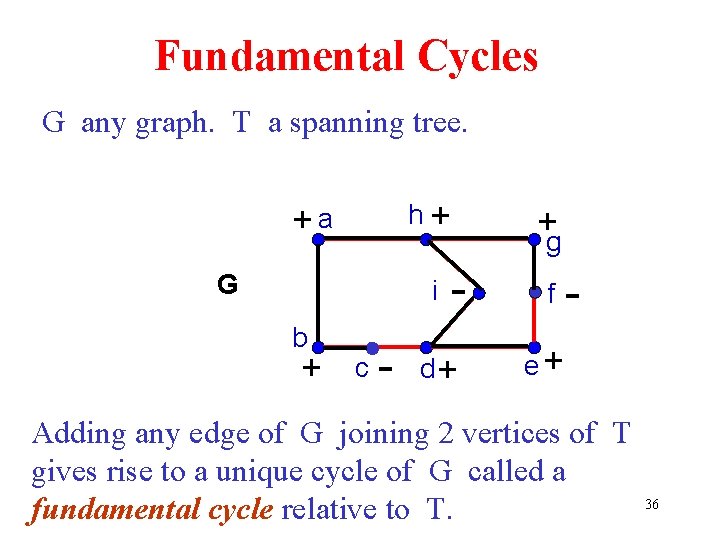
Fundamental Cycles G any graph. T a spanning tree. h+ +a G - f d+ e+ i b + c - +g - Adding any edge of G joining 2 vertices of T gives rise to a unique cycle of G called a fundamental cycle relative to T. 36

h+ +a T - f d+ e+ i b + c - +g - 37

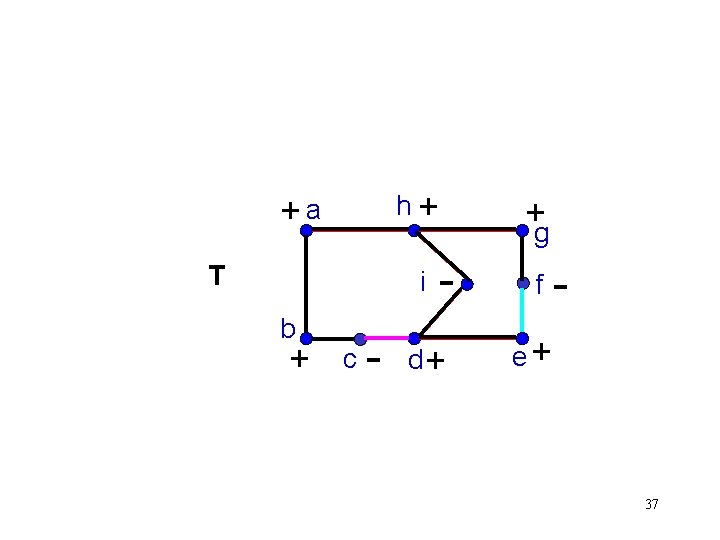
Characterization of Consistency II Theorem (Hoede 1992). Let G be a marked graph and T be a spanning tree of G. Then G is consistent iff 1). Every fundamental cycle relative to T is +; and 2). Each common path of a pair of fundamental cycles relative to T has end vertices with the same sign. 38

Characterization of Consistency II In the example: • The 2 fundamental cycles relative to T are + • There is only one common path of the pair of fundamental cycles, namely, d, i, h. • This path has both end vertices with the same sign. Thus, G is consistent. 39

Characterization of Consistency II Hoede’s Theorem provides an O(m 2 n) algorithm to check if a marked graph is consistent. (m = number of edges, n = number of vertices) R and Xu (2003) give an O(mn) algorithm. 40

Characterization of Consistency II Variant of Hoede’s Theorem: Theorem (R and Xu 2003). Let G be a marked graph and T be a spanning tree of G. Then G is consistent iff 1). Every fundamental cycle relative to T is +; and 2). Each 3 -connected vertex pair in G has the same sign. In example: h and d are the only 3 -connected pair. 41

Characterization of Consistency II Because checking for consistency of a marked graph is equivalent to checking for double balancedness of a bipartite graph, the following can be thought of as a bipartite analogue of R-Xu Theorem: Theorem (Conforti and Rao 1987). Let G be a bipartite graph and T be a spanning tree of G. Then G is double balanced iff 1). Every fundamental cycle relative to T has length congruent to 0 mod 4 ; and 2). Any cycle that is a symmetric difference of 2 fundamental cycles relative to T has length congruent 42 to 0 mod 4.

Characterization of Consistency II Conforti-Rao Theorem leads to an O(m 2 n) algorithm to determine if a bipartite graph is double balanced. R-Xu (2003) provide an O(mn) algorithm. 43

Cycle Bases Recall that a set K of cycles in a graph is a cycle basis if every cycle of G can be expressed as a symmetric difference of cycles in K and K is minimal. 44

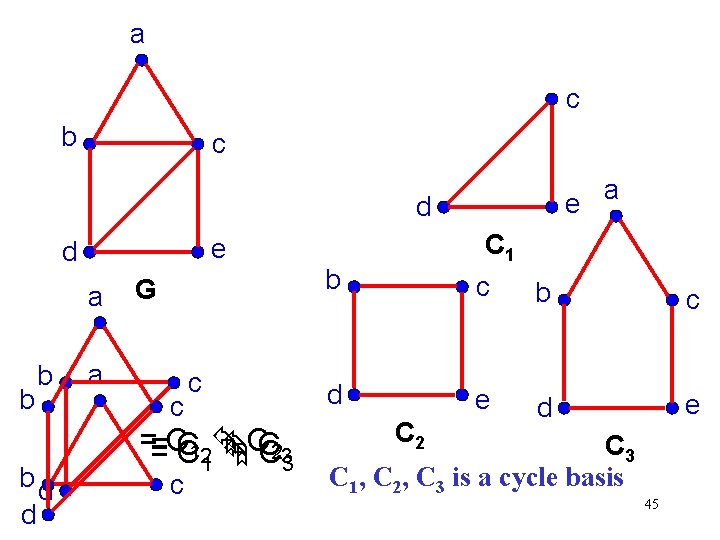
a c b c e d a b b bd d G a c c == =CC C 121 CC C 233 c a C 1 b c d e C 2 C 3 C 1, C 2, C 3 is a cycle basis 45

Characterization of Consistency III The set of fundamental cycles relative to a given spanning tree forms a cycle basis. Here is a generalization of Hoede’s Theorem: Theorem (R and Xu, 2003). Let G be a marked graph and B be any cycle basis of G. Then G is consistent iff 1). Every cycle in B is +; and 2). Each 3 -connected vertex pair in G has the same sign. This theorem leads to the O(mn) algorithm to test for 46 consistency.

The Markability Problem Given G unmarked. Can always mark it consistently: Use all + signs. What if at least one – sign is required? Then even K 4 cannot be consistently marked. G is markable if it can be consistently marked using at least one – sign. Problem: When is a graph markable? Problem: Find a “structure theorem” that characterizes markable graphs. 47

3 -Connected Markable Graphs Theorem (R 1995). If graph G is 3 -connected, then G is markable iff it is bipartite. Proof: Straightforward using Menger’s Theorem. Thus, we may concentrate on graphs that are not 3 connected. 48

Markable Blocks Recall that a block is a connected graph with more than one vertex and no cutpoints. A block in a graph is a maximal subgraph that is a block. A graph is 2 -connected iff it is a block consisting of more than one edge. 49

Markable Blocks Observation: A graph is markable if every block is markable. (Trivial by induction on number of blocks. ) The converse is false. 50

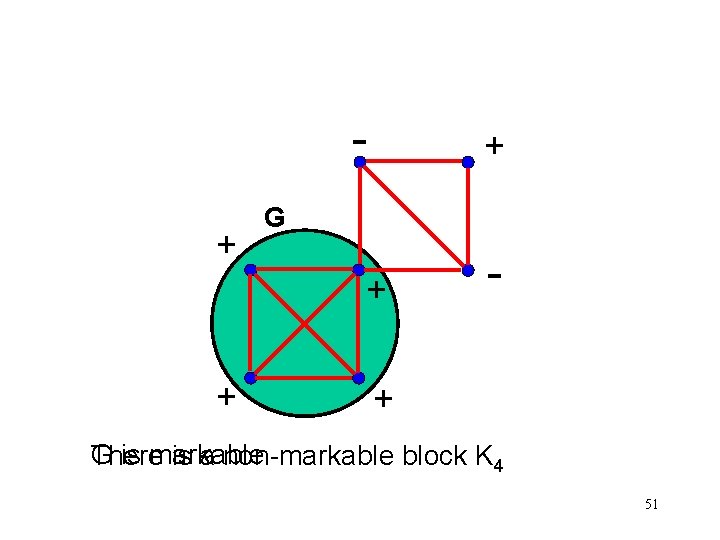
+ + G + + - + G is markable There is a non-markable block K 4 51

Markable Blocks Observation (Trotter): A structure theorem for markable graphs that are not blocks is impossible. Given any graph G, G is an induced subgraph of a markable graph. 52

Markable Blocks Some examples of Markable Blocks. K(p, q) Complete bipartite graph with p vertices in one class and q in the other. K(2, q) is markable. Make the class of 2 vertices + and the other class –. 54

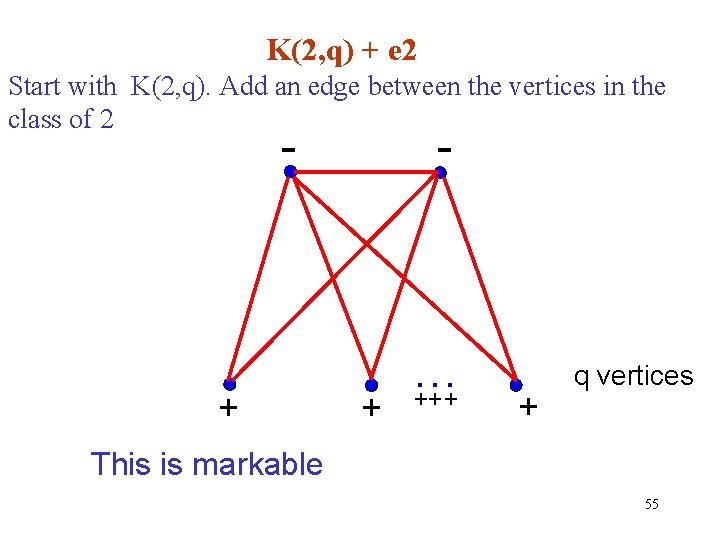
K(2, q) + e 2 Start with K(2, q). Add an edge between the vertices in the class of 2 - - + + … +++ + q vertices This is markable 55

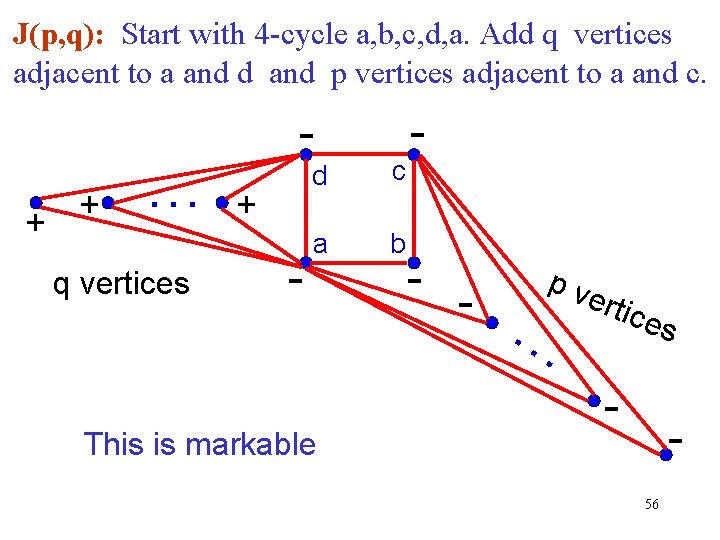
J(p, q): Start with 4 -cycle a, b, c, d, a. Add q vertices adjacent to a and d and p vertices adjacent to a and c. + + … q vertices + - d c a b This is markable - - - pv … erti ces - 56

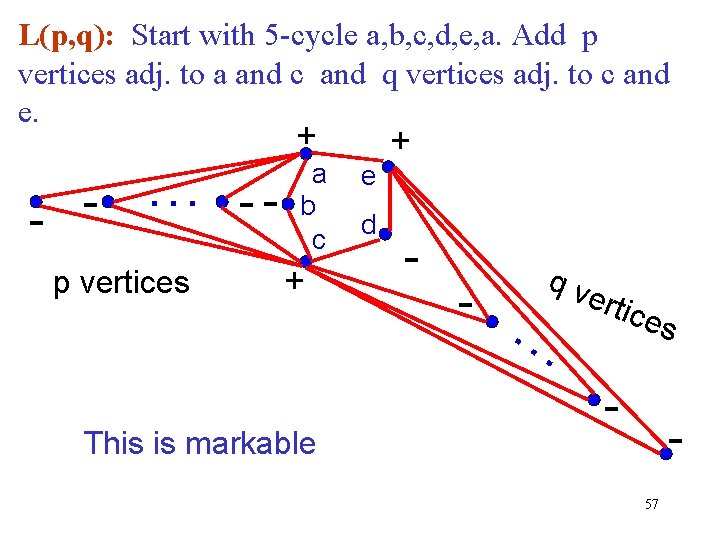
L(p, q): Start with 5 -cycle a, b, c, d, e, a. Add p vertices adj. to a and c and q vertices adj. to c and e. - … p vertices + -- a b c + This is markable e d + - - qv … erti ces - 57

Markable Blocks Theorem (R): Suppose that G is a block with no cycle of length greater than 5. Then G is markable iff G is K 2; K 3; K(2, q) for q 2; K(2, q) + e 2 for q 2; J(p, q) for p 0, q 1; or L(p, q) for p, q 0. 58

Open Questions 1. Give a structural characterization of markable blocks with longer cycles. 59

Open Questions 2. Lots of work has been done on degrees of balance. Introduce similar notions of degree of consistency. (E. g. : line index for balance = smallest # edges whose removal gives balance. Vertex index of consistency = smallest # vertices whose removal gives consistency. ) 60

Open Questions 3. Introduce similar degrees of markability. E. g. : What is smallest # of vertices whose removal results in a markable graph? 61