On a trie partitioning algorithm for powerefficient TCAMs

On a trie partitioning algorithm for power-efficient TCAMs Authors: Haibin Lu Presenter: Yi-Sheng, Lin (林意勝) Date: 2009. 3. 11 Publisher/Conf. : INTERNATIONAL JOURNAL OF COMMUNICATION SYSTEMS Dept. of Computer Science and Information Engineering National Cheng Kung University, Taiwan R. O. C. 1

Outline 1. 2. 3. 4. Introduction Related Work LOGSPLIT: A New Trie-Partitioning Algorithm Experiment 2

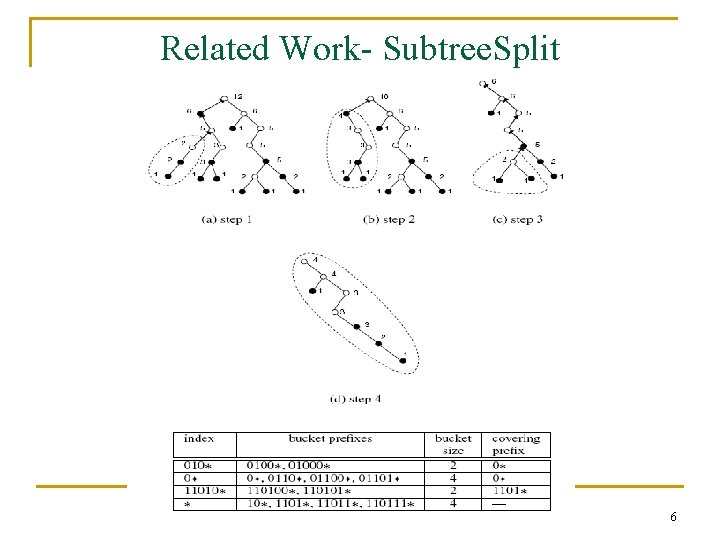
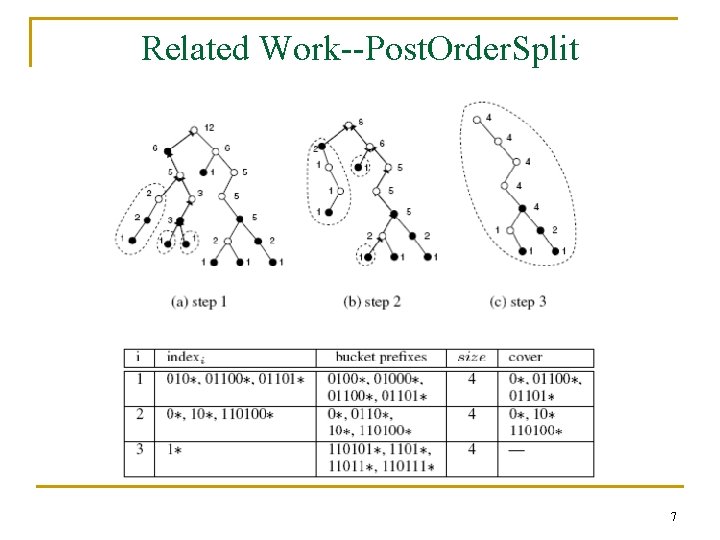
Introduction(1/2) n Zane et al. [3] use two partitioning algorithms to reduce the number of TCAM entries that are checked during lookup. The schemes use multiple TCAMs or a single TCAM with multiple blocks. n Subtree. Split may waste many entries of data TCAM, and thus is too space-inefficient to be practical. n Post. Order. Split fully utilizes each data TCAM block except the last one. However, it generates a large index TCAM. Each data TCAM block contributes up to W + 1 entries to the index TCAM. [3]. Zane F, Narlikar G, Basu A. Cool. CAMs: power-efficient TCAMs forwarding engines. IEEE INFOCOM, San Francisco, CA, U. S. A. , 2003. 3

Introduction(2/2) n Since the index TCAM is always on, its power consumption is significant, especially for IPv 6 router tables. n The router hardware designers have to use the worst-case bound to determine the size of an index TCAM and the power budget. n The contribution of this paper is a new trie-partitioning algorithm, Log. Split, in which each data TCAM block adds at most log 2 m entries to the index TCAM, where m is the number of entries in one data TCAM block. 4

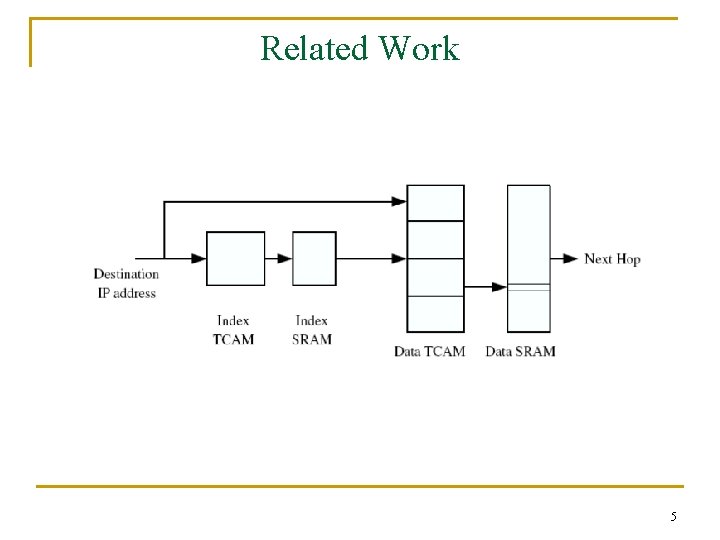
Related Work 5

Related Work- Subtree. Split 6

Related Work--Post. Order. Split 7

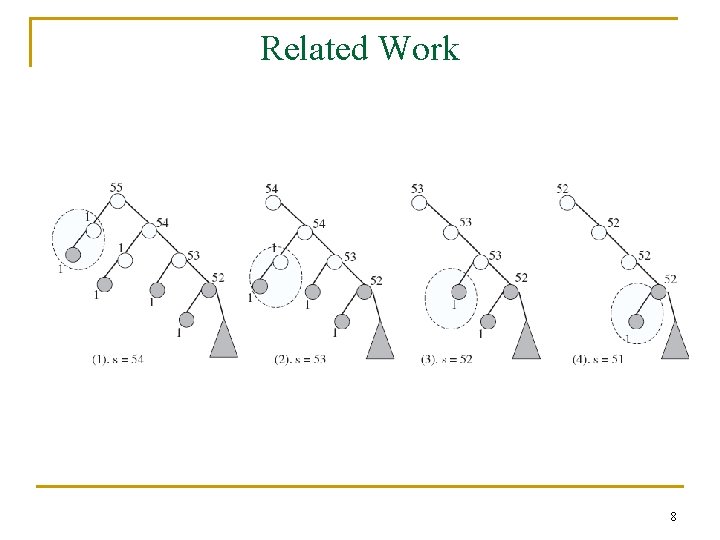
Related Work 8

LOGSPLIT: A New Trie-Partitioning Algorithm n If count(x)>s where s is a positive integer, then there is a node y in subtrie(x) such that 9

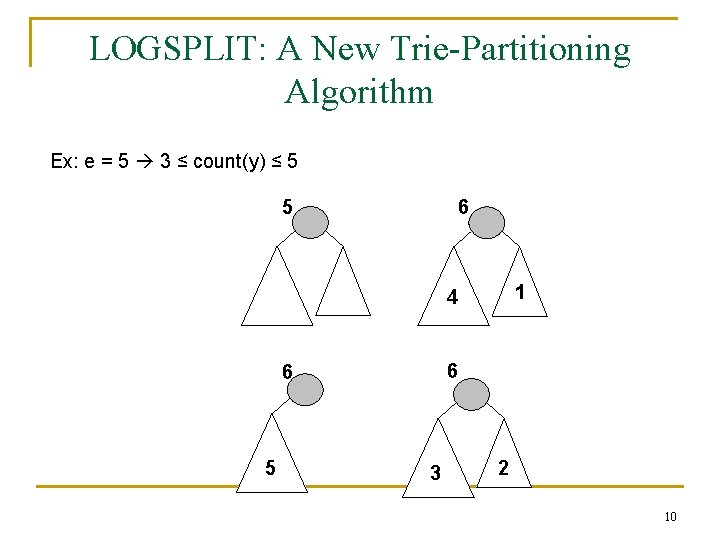
LOGSPLIT: A New Trie-Partitioning Algorithm Ex: e = 5 3 ≤ count(y) ≤ 5 5 6 1 4 6 6 5 3 2 10

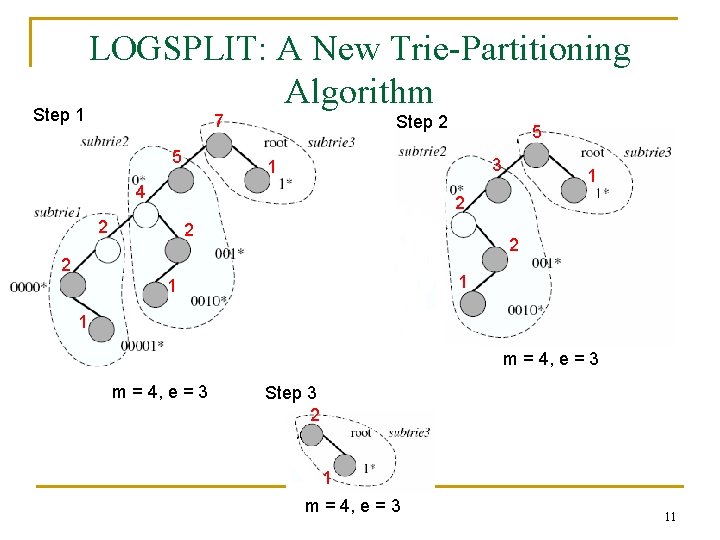
LOGSPLIT: A New Trie-Partitioning Algorithm Step 1 7 5 Step 2 5 3 1 4 1 2 2 2 1 1 1 m = 4, e = 3 Step 3 2 1 m = 4, e = 3 11

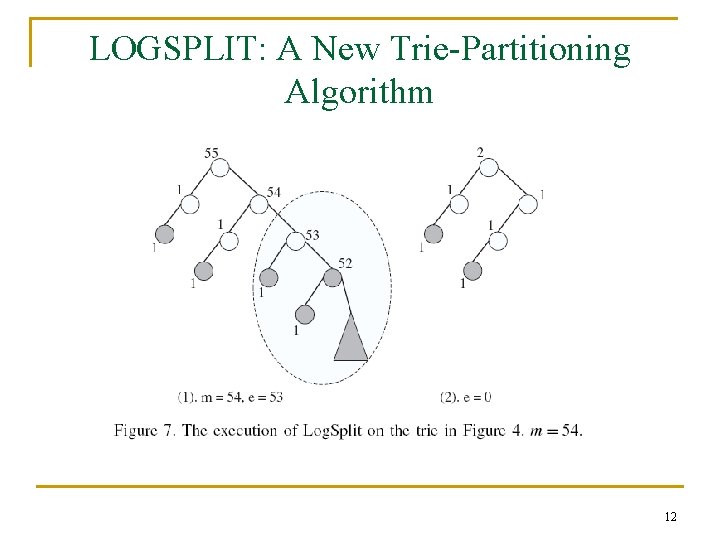
LOGSPLIT: A New Trie-Partitioning Algorithm 12

LOGSPLIT: A New Trie-Partitioning Algorithm 13

LOGSPLIT: A New Trie-Partitioning Algorithm n The algorithm makes at most log 2 m iterations to fill each bucket and each iteration invokes get. Node. Y(), which takes O(W) time each. Hence, it takes O(W log 2 m) time to fill each bucket. n The total time of adding the prefixes to the buckets is the size of the trie, which is O(n. W). n Therefore, the overall time complexity of Log. Split is O(n. W). n The time complexities of Subtree. Split and Post. Order. Split [3] are also O(n. W). 14

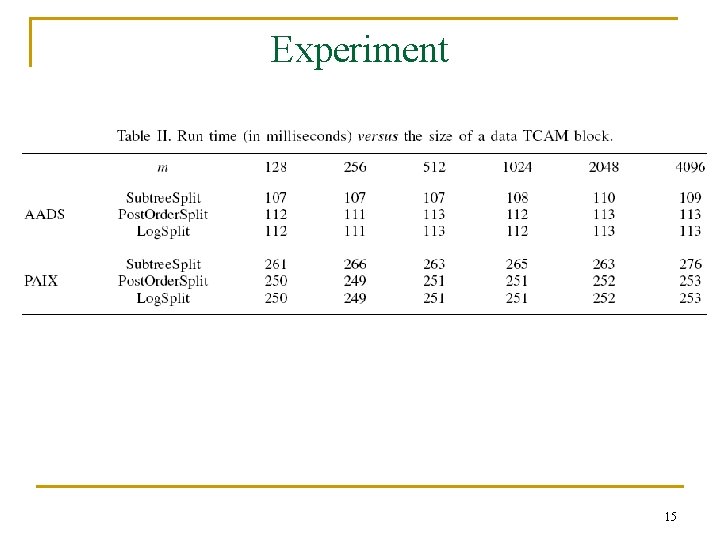
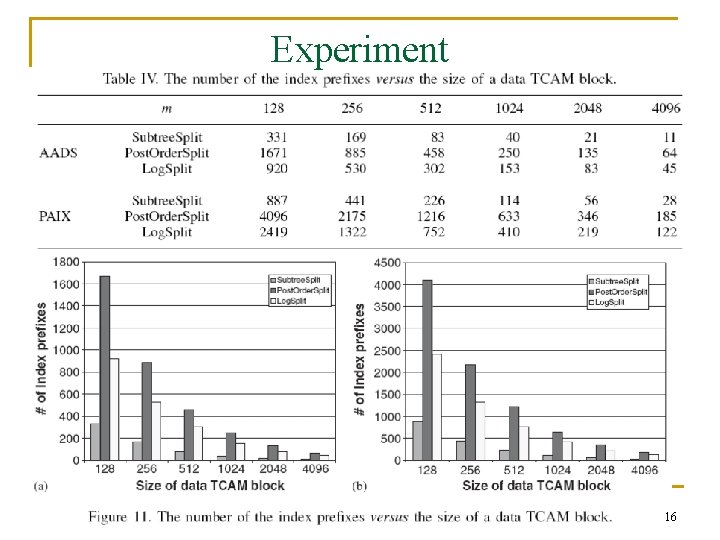
Experiment 15

Experiment 16

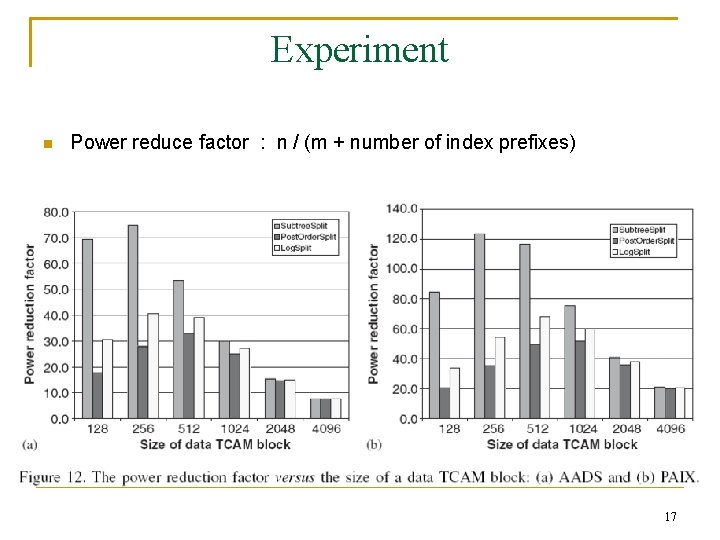
Experiment n Power reduce factor : n / (m + number of index prefixes) 17

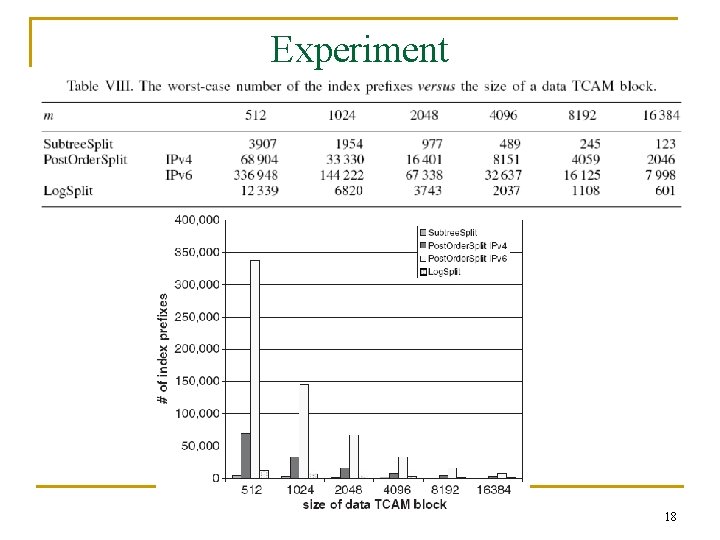
Experiment 18

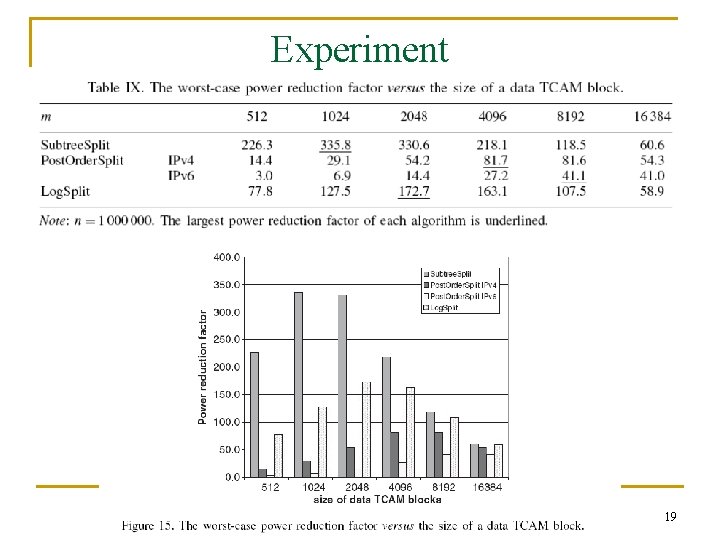
Experiment 19

Conclusion n In this paper we develop a new trie-partitioning algorithm, Log. Split, to reduce power consumption. Each data TCAM block contributes at most log 2 m entries to the index TCAM for both IPv 4 and IPv 6, where m is the maximum number of entries in one data TCAM block. n Since the index TCAM is always enabled for search and it counts for a significant portion of the overall power consumption, especially when m is small, reducing the size of the index TCAM makes lookup engines cooler. 20