On a Theory of Media Processing Systems Behaviour

On a Theory of Media Processing Systems Behaviour, with Applications M. A. Weffers-Albu, J. J. Lukkien, E. F. M. Steffens, P. D. V. v. d. Stok Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 1

Contents • Domain introduction • Relevant issues • Related work • Approach • Model • Conclusions Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 2
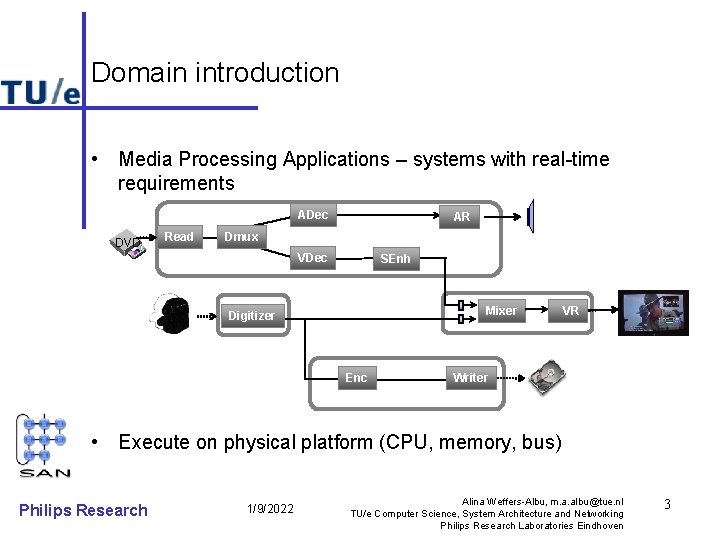
Domain introduction • Media Processing Applications – systems with real-time requirements ADec DVD Read AR Dmux VDec SEnh Mixer Digitizer Enc VR Writer • Execute on physical platform (CPU, memory, bus) Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 3
Domain introduction Media Processing Applications … Physical Platform Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 4

Domain introduction Media Processing Applications … Physical Platform Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 5
Domain introduction Media Processing Applications … Physical Platform Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 6
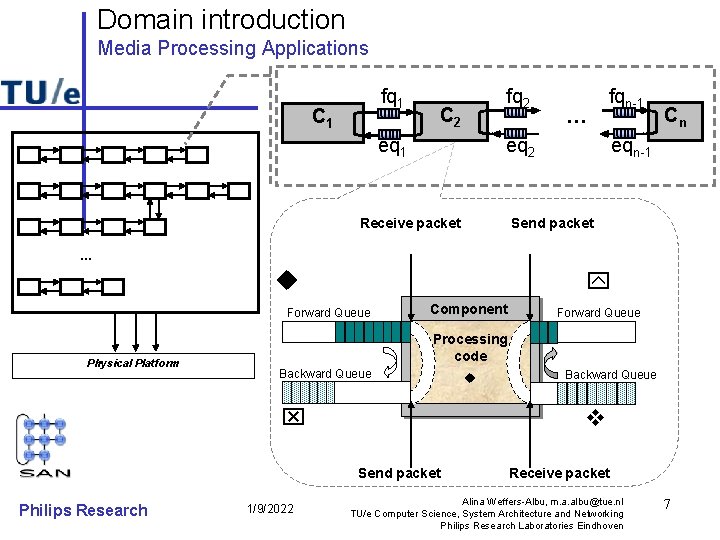
Domain introduction Media Processing Applications fq 1 C 1 fq 2 C 2 eq 1 … fqn-1 eq 2 Receive packet Cn eqn-1 Send packet … Forward Queue Physical Platform Component Processing code Backward Queue 1/9/2022 Backward Queue Send packet Philips Research Forward Queue Receive packet Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 7

Relevant Issues When constructing / modifying an application: • How much resources does the application need? • Will the application meet its timing requirements? • What is the minimum of the resources needed such that timing requirements are met? • What can one do to reduce the resource needs of the application? • What can be done to improve the measure in which the application meets timing requirements? Need to predict, control the overall behavior of the application Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 8

Relevant Issues Calculate / Optimize: – response time of tasks, chain, – necessary and sufficient buffer capacities – number of context switches (cost associated) Need model for dynamic behavior of system. Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 9

Related work • Classical RT theory does not help directly – Mainly periodic independent tasks – Tasks with precedence constraints • Previous work in domain: – Estimations for some parameters (Lowet) – Reduce the problem to an equivalent one where tasks could be treated as independent periodic (Goddard, Groba). • Our approach: – Calculate parameters rather than estimate – Uses the fact that tasks are dependent rather than reduce it into a classical RT problem • Contribution of paper: – foundations of theory for engineers to reason rigorously about system behavior and associated resource needs. Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 10

Approach • First step – single linear chain executing in cooperative environment • Express the execution of the system (chain) as a trace of the atomic actions taken by each component. • Analyze the system in terms of time and behaviour as a function of: – – Philips Research the choice of the atomic action order in the components; the channel properties (e. g. , the capacity); the priority assignment; the timing assignment. 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 11

Approach Basic concepts • Component program example: C: {a; b; c; d; } • Component alphabet: set of actions taken by the component (A(C)={a, b, c, d}). Alphabets disjoint: k l, A(Ck) A(Cl) = . • Trace of a component: sequence of actions of a component, recording its execution. Tr(C) : {(a b c d)} • Trace prefix: Tr(C)={(abcd)}, Pref(Tr(C)) = {(a), (a b c), (a b c d)} Prefix = State; Pref(Tr(C)) = St(Tr(C)) • Parallel composition of components: arbitrary interleaving of actions: Ck || Cl, with Ck : {a; b} and Cl : {c; d}; Tr(Ck||Cl)= {(a b c d), (a c b d), (c a d b), (c d a b), (a c d b), (c a b d)} Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 12

Approach Basic concepts • Projection of a trace on an alphabet (t↑A): trace obtained by removing all actions not in A while maintaining the order given in t. t=(abcd), A(Ck) = {a, b}, t↑A = (ab) • • #(t, a) = nb. of occurences of action a in trace t. Ci: while (true) do { receive( fqi-1, p); receive( eqi, q); process_fct(p, q); send( eqi-1, p); send( fqi, q); } Philips Research 1/9/2022 fqi! fqi-1? ci eqi-1! eqi? Tr(Ci): { (fqi-1? eqi? ci eqi-1! fqi!)ω} for 1 i n. Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 13
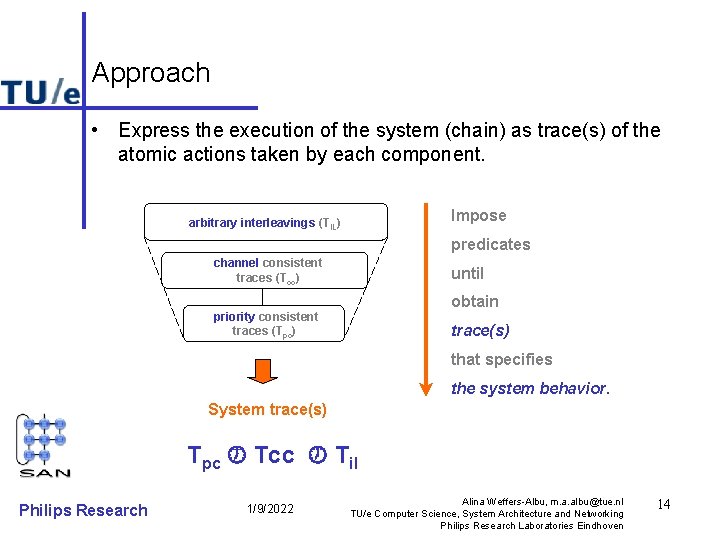
Approach • Express the execution of the system (chain) as trace(s) of the atomic actions taken by each component. Impose arbitrary interleavings (TIL) predicates channel consistent traces (Tcc) until obtain priority consistent traces (Tpc) trace(s) that specifies the system behavior. System trace(s) Tpc Tcc Til Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 14

Arbitrary interleavings traceset (Til) • A= arbitrary interleavings (Til) channel consistent traces (Tcc) A(Ci), priority consistent traces (Tpc) System trace(s) • Til = Tr( Ci ) • Til = {s: s consists of elements of A ∧ s↑A(Ci) Tr(Ci), i, i =1. . n} Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 15

Introducing channel constraints • Scc imposes that no buffer is allowed to overflow or underflow. arbitrary interleavings (Til) channel consistent traces (Tcc) priority consistent traces (Tpc) System trace(s) • Scc(t): ( s Pref(t), fqi, eqi (1≤ i < n): 0 ≤ #(t, fqi!) - #(t, fqi? ) ≤ Cap( fqi) ∧ 0 ≤ #(t, eqi!) - #(t, eqi? ) ≤ Cap( eqi )). • Tcc = {t Til| Scc(t)} – channel consistent traces. Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 16

Introducing channel constraints Definitions – ready and blocked actions arbitrary interleavings (Til) channel consistent traces (Tcc) • Tcc constrained set • Given s from St(Tcc), a component Ci is ready-to-run in state s when for an action a in A(Ci) such that sa↑ A(Ci) is a state of Tr(Ci) we have that sa St(Tcc). Also, a is called a ready action of Ci in state s. priority consistent traces (Tpc) System trace(s) sa ↑ A(Ci) sa St(Tcc) a is a ready action in state s • If sa is not an element of St(Tcc) it is not possible to execute a in the constrained set in which case we say that Ci is blocked at a in state s of Tcc. sa ↑ A(Ci) sa St(Tcc) a is a blocked action in state s Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 17
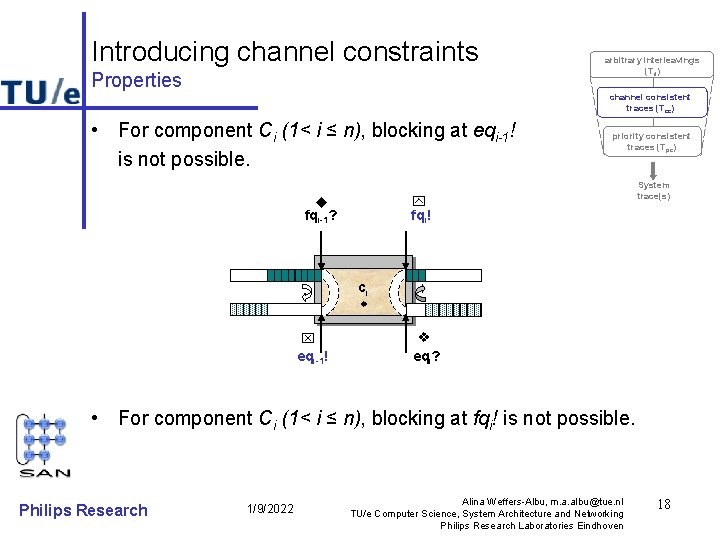
Introducing channel constraints Properties arbitrary interleavings (Til) channel consistent traces (Tcc) • For component Ci (1< i ≤ n), blocking at eqi-1! is not possible. priority consistent traces (Tpc) fqi! fqi-1? System trace(s) ci eqi-1! eqi? • For component Ci (1< i ≤ n), blocking at fqi! is not possible. Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 18

Introducing precedence order constraints arbitrary interleavings (Til) channel consistent traces (Tcc) • Priority – function returning for each component a unique natural number. priority consistent traces (Tpc) – The assignation is fixed during the entire execution of the system. System trace(s) • Scp(t): ( s Pref(t), ai u A : t = saiu ∧ ai A(Ci): P(Comp(ai))= max P(C)). C RR(s) • Limiting Tcc according to Scp gives Tpc, the priority consistent traces: Tpc = { t Tcc| Scp(t)}. Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 19
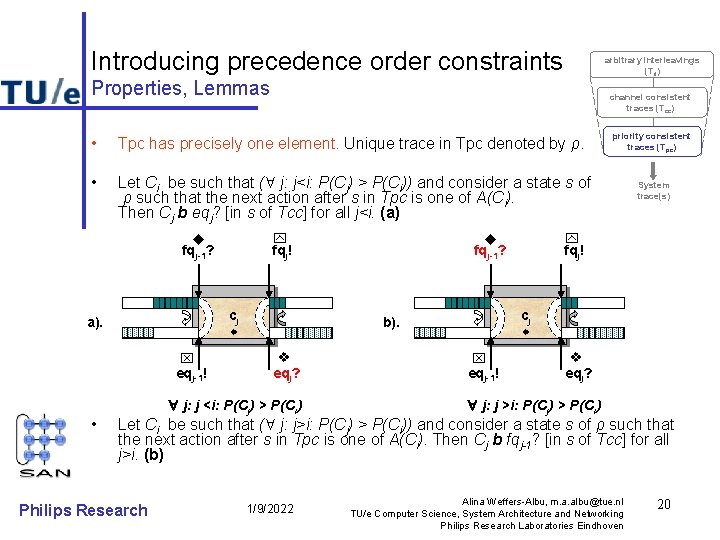
Introducing precedence order constraints arbitrary interleavings (Til) Properties, Lemmas channel consistent traces (Tcc) • Tpc has precisely one element. Unique trace in Tpc denoted by ρ. • Let Ci be such that ( j: j<i: P(Cj) > P(Ci)) and consider a state s of ρ such that the next action after s in Tpc is one of A(Ci). Then Cj b eqj? [in s of Tcc] for all j<i. (a) fqj! fqj-1? cj a). eqj-1! • j: j <i: P(Cj) > P(Ci) System trace(s) fqj! fqj-1? cj b). eqj? priority consistent traces (Tpc) eqj-1! eqj? j: j >i: P(Cj) > P(Ci) Let Ci be such that ( j: j>i: P(Cj) > P(Ci)) and consider a state s of ρ such that the next action after s in Tpc is one of A(Ci). Then Cj b fqj-1? [in s of Tcc] for all j>i. (b) Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 20

arbitrary interleavings (Til) Stable phase characterization channel consistent traces (Tcc) Theorems, Properties, Corollaries priority consistent traces (Tpc) Theorem. The pipeline system assumes a repetitive behavior after a finite initialization phase. The complete behavior is characterized by ρ = tinit (fqm-1? eqm? cm eqm-1! t. L fqm! Execution in cascade of sub-chain t R )ω Execution in cascade of sub-chain … C 1 System trace … Cm-1 - all backward queues empty. Cm+1 Cn - all forward queues empty. Notation. tinit – trace recording the initialization phase of the system execution. tstable = (fqm-1? eqm? cm eqm-1! t. L fqm! t. R)ω. tstable - trace recording the stable phase of the system execution. Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 21

arbitrary interleavings (Til) Stable phase characterization channel consistent traces (Tcc) Theorems, Properties, Corollaries priority consistent traces (Tpc) Theorem. The pipeline system assumes a repetitive behavior after a finite initialization phase. The complete behavior is characterized by ρ = tinit (fqm-1? eqm? cm eqm-1! t. L fqm! t. L t. R tinit t. L t. R System trace t R )ω t. L t. R … tstable Notation. tinit – trace recording the initialization phase of the system execution. tstable = (fqm-1? eqm? cm eqm-1! t. L fqm! t. R)ω. tstable - trace recording the stable phase of the system execution. Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 22

Stable phase characterization arbitrary interleavings (Til) Theorems, Properties, Corollaries • The length of the initialization phase in number of channel consistent traces (Tcc) priority consistent traces (Tpc) System trace actions is + (m-1). • The length of the initialization phase can be reduced by decreasing m or the capacity of the queues in the system. • The stable phase starts when Cm executes for the first time. • When Cm executes, i: 1 ≤ i < m, L(fqi)=Cap(fqi)-1 ∧ L(eqi)=0 ∧ i: m ≤ i < n, L(fqi) = 0 ∧ L(eqi)=Cap(eqi). Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 23

Stable phase characterization Theorems, Properties, Corollaries arbitrary interleavings (Til) channel consistent traces (Tcc) priority consistent traces (Tpc) Minimum NCS System trace a. The minimum number of context switches (NCS) during the initialization phase is achieved when m=1. b. The minimum NCS during one iteration of tstable can be achieved either when: i. P(C 1) = min(P(C i)) i = 1. . n Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 24
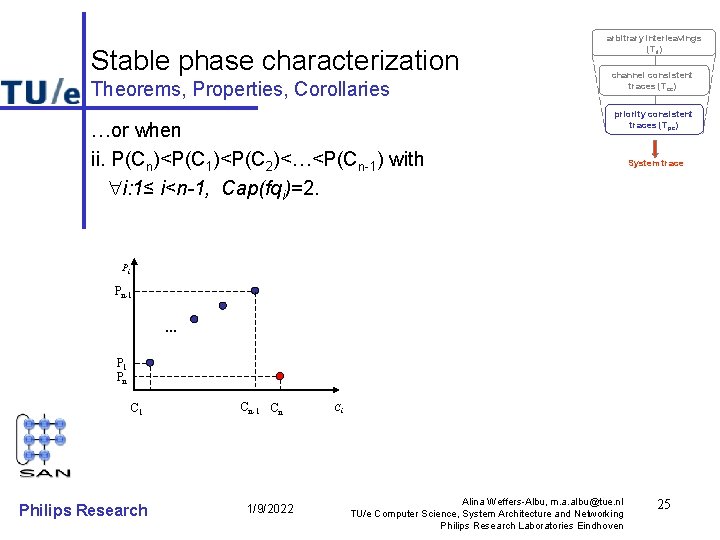
Stable phase characterization Theorems, Properties, Corollaries …or when ii. P(Cn)<P(C 1)<P(C 2)<…<P(Cn-1) with i: 1≤ i<n-1, Cap(fqi)=2. arbitrary interleavings (Til) channel consistent traces (Tcc) priority consistent traces (Tpc) System trace Pi Pn-1 … P 1 Pn C 1 Philips Research Cn-1 Cn 1/9/2022 Ci Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 25

Stable phase characterization arbitrary interleavings (Til) Theorems, Properties, Corollaries Tradeoff • The priority assignment suggested by Corollary 10 - ii implies that all context switches caused by preemptions were eliminated, at the cost of an initialization phase. channel consistent traces (Tcc) priority consistent traces (Tpc) System trace • The priority assignment suggested by Corollary 10 - ii. achieves a minimum NCS at the cost of more memory needed ( i: 1 ≤ i < n-1, Cap(fqi)=2) Optimizing memory needs. • The minimum queue capacity necessary and sufficient for each of the queues in the chain is 1. Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 26

arbitrary interleavings (Til) Timing aspects channel consistent traces (Tcc) priority consistent traces (Tpc) Definitions System trace • : Ax x Til that for each action of a component Ci returns the computation time needed to execute the action. • Schedule function : A x x Til of the concurrent execution of Ci, i=1. . n processes on a processor. Returns the start time for each action of each component Ci within the concurrent execution of all components. Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 27

arbitrary interleavings (Til) Timing aspects channel consistent traces (Tcc) priority consistent traces (Tpc) Definitions Response time Ri, k of component Ci (1 i n) that processes packet k is: Ri, k = (fqi !k) + (fqi !k) - (fqi-1? k). System trace Response time of the chain (RTC) CN as the time needed by all components in the chain to process the kth packet: RTCk = (fq. N!k) + (fq. N!k) - (fq 0? k). NAk is the number of actions occurring from arrival of packet k until the packet leaves the chain. Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 28

arbitrary interleavings (Til) Timing aspects channel consistent traces (Tcc) priority consistent traces (Tpc) System trace • NAk is minimal for all packets k when P(C 1) = imin P(Ci) = 1. . n • RTCk is minimal for all packets k when P(C 1) = min P(Ci) Philips Research 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 29

Conclusions • Presented a model for the dynamic behavior of linear processing chains • Expressed the execution of a chain as a trace that can be calculated at design time. • Formally proven that the trace becomes repetitive after an initial finite prefix. • Approach allows the calculation and optimization of – – – Philips Research The initial phase length The necessary and sufficient capacities for the queues Number of context switches Number of actions between input/output of a packet (component, chain) Response time for a packet (component, chain) 1/9/2022 Alina Weffers-Albu, m. a. albu@tue. nl TU/e Computer Science, System Architecture and Networking Philips Research Laboratories Eindhoven 30
- Slides: 30