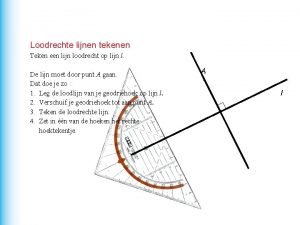
Omtrekshoeken Stelling van de constante hoek Voor de

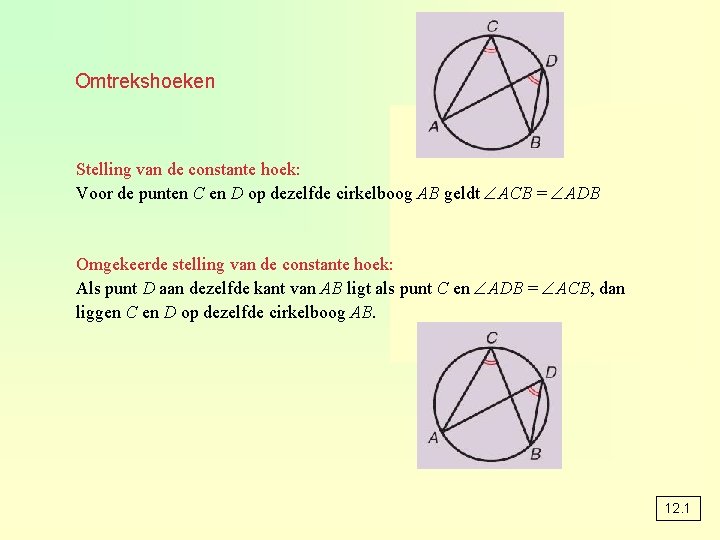
Omtrekshoeken Stelling van de constante hoek: Voor de punten C en D op dezelfde cirkelboog AB geldt ACB = ADB Omgekeerde stelling van de constante hoek: Als punt D aan dezelfde kant van AB ligt als punt C en ADB = ACB, dan liggen C en D op dezelfde cirkelboog AB. 12. 1

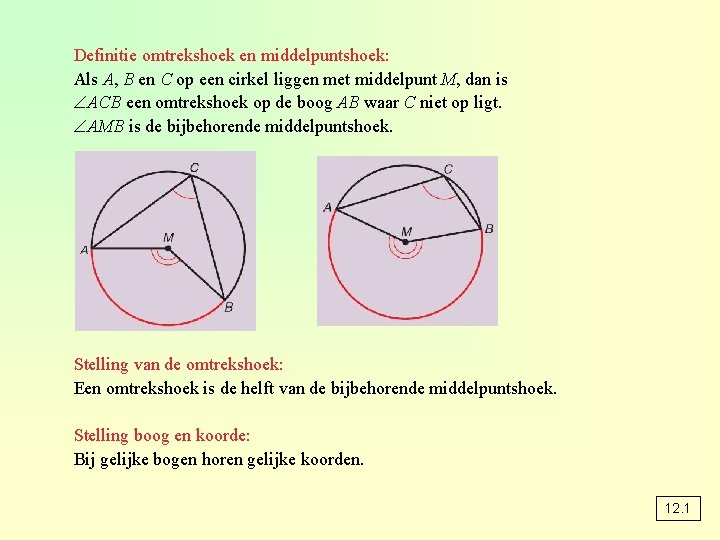
Definitie omtrekshoek en middelpuntshoek: Als A, B en C op een cirkel liggen met middelpunt M, dan is ACB een omtrekshoek op de boog AB waar C niet op ligt. AMB is de bijbehorende middelpuntshoek. Stelling van de omtrekshoek: Een omtrekshoek is de helft van de bijbehorende middelpuntshoek. Stelling boog en koorde: Bij gelijke bogen horen gelijke koorden. 12. 1

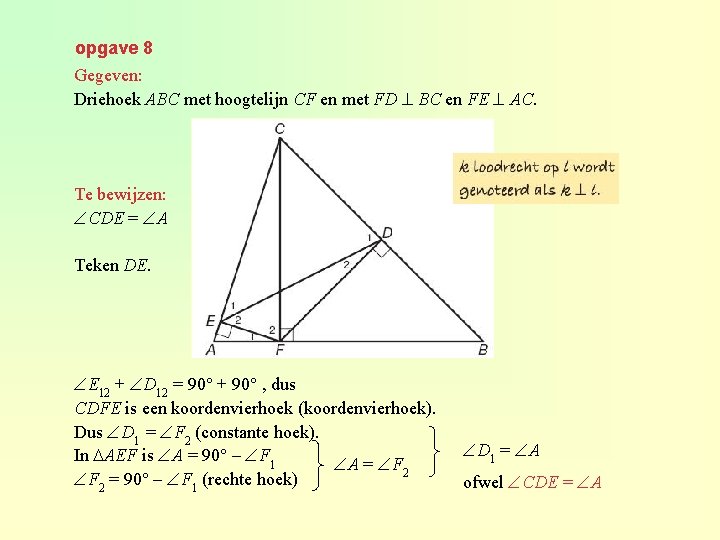
opgave 8 Gegeven: Driehoek ABC met hoogtelijn CF en met FD BC en FE AC. Te bewijzen: CDE = A Teken DE. E 12 + D 12 = 90° + 90° , dus CDFE is een koordenvierhoek (koordenvierhoek). Dus D 1 = F 2 (constante hoek). In AEF is A = 90° – F 1 A = F 2 = 90° – F 1 (rechte hoek) D 1 = A ofwel CDE = A

opgave 12 a Gegeven: De punten A, B, C en D op een cirkel zo, dat de lijnen AB en CD elkaar binnen de cirkel snijden in punt P. Te bewijzen: PA · PB = PC · PD ■ Bewijs: Teken de lijnstukken AC en BD. A = D (constante hoek) B = C (constante hoek) Hieruit volgt dus PA · PB = PC · PD. ● ■ ●

opgave 12 b Gegeven: De punten A, B, C en D op een cirkel zo, dat de lijnen AB en CD elkaar buiten de cirkel snijden in punt P. Te bewijzen: PA · PB = PC · PD 1 2 Bewijs: Teken de lijnstukken AC en BD. A + D 1 = 180° (koordenvierhoek) D 2 + D 1 = 180° (gestrekte hoek) Hieruit volgt dus PA · PB = PC · PD. A = D 2 P = P APC ∾ DPB (hh)

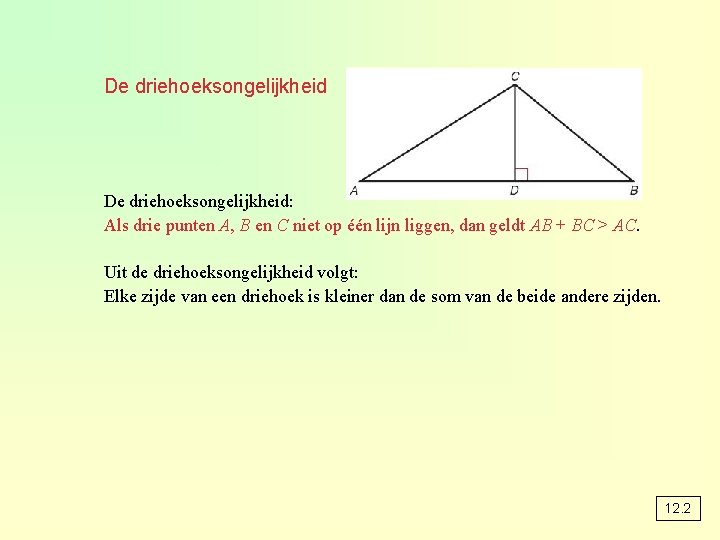
De driehoeksongelijkheid: Als drie punten A, B en C niet op één lijn liggen, dan geldt AB + BC > AC. Uit de driehoeksongelijkheid volgt: Elke zijde van een driehoek is kleiner dan de som van de beide andere zijden. 12. 2

opgave 16 Gegeven: Driehoek ABC met punt P binnen de driehoek. Te bewijzen: PA + PB + PC > s Bewijs: Teken de lijnstukken PA, PB en PC. PA + PB > c (driehoeksongelijkheid) PB + PC > a (driehoeksongelijkheid) PC + PA > b (driehoeksongelijkheid) P ● 2 PA + 2 PB + 2 PC > a + b + c PA + PB + PC > (a + b + c) PA + PB + PC > s

Een bolleboos riep laatst met zwier Gewapend met een vel A-vijf: ‘Er is geen allergrootst getal, Dat is wat ik bewijzen ga. Stel, dat ik nu zou bedriegen En hier een potje stond te jokken, Dan zou ik zonder overdrijven Het grootste kunnen op gaan noemen. Maar ben ik klaar, roep u meteen “vermeerder dat getal met twee!”

Dan zien we zeker en gewis Dat dit toch niet het grootste was. En gaan we zo nog door een poos, Dan merkt u: dit is onbegrensd. En daarmee heb ik q. e. d. Ik ben hier diep gelukkig door. Zo gaan, ’zei hij voor hij bezwijmde, ‘bewijzen uit het ongedichte. ’

Bewijs uit het ongerijmde Werkschema: bewijs uit het ongerijmde 1. Formuleer het Gegeven en het Te bewijzen. 2. Veronderstel dat het Te bewijzen niet juist is. 3. Toon aan dat deze veronderstelling leidt tot een tegenspraak. 4. Uit deze tegenspraak volgt dat het Te bewijzen juist is. 5. 6. Met het bewijs uit het ongerijmde bewijzen we de stelling van een raaklijn aan een cirkel. 7. 8. 9. Definitie van raaklijn aan cirkel: Een raaklijn aan een cirkel is een lijn die precies één punt gemeenschappelijk heeft met de cirkel. 10. Stelling van raaklijn aan cirkel: 11. Een raaklijn aan een cirkel staat loodrecht 12. op de straal naar het raakpunt. 12. 2

Bewijs uit het ongerijmde Stel AM staat niet loodrecht op raaklijn k. Dan is er een hoek tussen MA en lijn k < 90 graden Bij deze hoek hoort een middelpuntshoek die het dubbele is en dus <180 graden. Dus er ligt een punt C op de cirkel die ook op k ligt en niet gelijk is aan punt A. Maar k heeft maar één punt gemeenschappelijk met C dus kan de veronderstelling niet juist zijn en is de hoek tussen de raaklijn en AM wel 90 graden. 12. 2

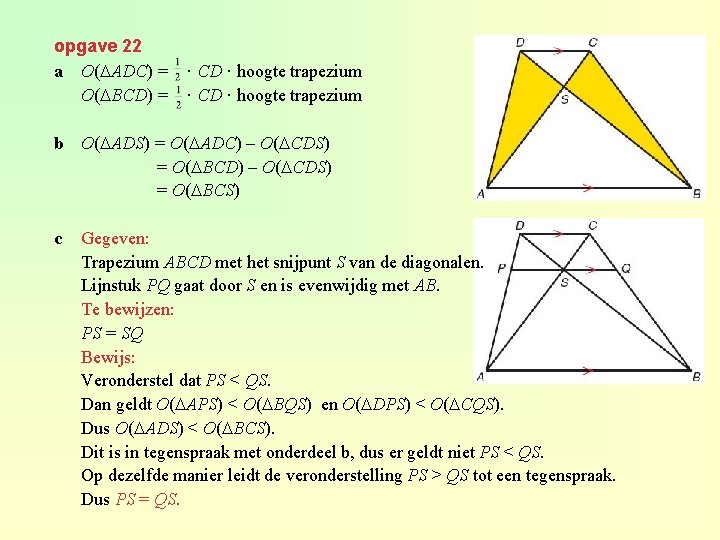
opgave 22 a O( ADC) = O( BCD) = · CD · hoogte trapezium b O( ADS) = O( ADC) – O( CDS) = O( BCD) – O( CDS) = O( BCS) c Gegeven: Trapezium ABCD met het snijpunt S van de diagonalen. Lijnstuk PQ gaat door S en is evenwijdig met AB. Te bewijzen: PS = SQ Bewijs: Veronderstel dat PS < QS. Dan geldt O( APS) < O( BQS) en O( DPS) < O( CQS). Dus O( ADS) < O( BCS). Dit is in tegenspraak met onderdeel b, dus er geldt niet PS < QS. Op dezelfde manier leidt de veronderstelling PS > QS tot een tegenspraak. Dus PS = QS.

Hoek tussen koorde en raaklijn Stelling van de hoek tussen koorde en raaklijn: De hoek tussen een raaklijn aan een cirkel en een koorde van die cirkel waarvan een eindpunt het raakpunt is, is even groot als de niet-stompe omtrekshoek die bij deze koorde hoort. 12. 2

opgave 27 Gegeven: De punten A, B en C op een cirkel met de raaklijn in C evenwijdig met koorde AB. Te bewijzen: ABC is gelijkbenig. C ● 1 3 > > ●B 2 Bewijs: Teken AC en BC. A● B = C 3 (Z-hoeken) A = C 3 (hoek tussen koorde en raaklijn) Dus ABC is een gelijkbenige driehoek. B = A

Afstand van punt tot gebied Onder een gebied verstaan we een gedeelte van het vlak waarbij de rand tot het gebied behoort. We noteren de afstand van P tot G als d(P, G) = PQ Definitie afstand van punt tot gebied: De afstand van een punt P tot een gebied G is de lengte van het kortste verbindingslijnstuk tussen P en een punt van G. Stelling van afstand punt tot lijn: De afstand van een punt tot een lijn is de lengte van het loodlijnstuk vanuit dat punt op die lijn. 12. 3

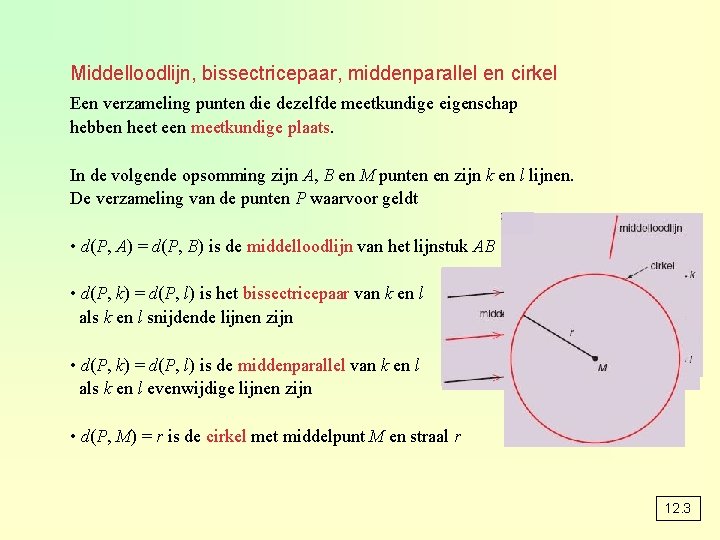
Middelloodlijn, bissectricepaar, middenparallel en cirkel Een verzameling punten die dezelfde meetkundige eigenschap hebben heet een meetkundige plaats. In de volgende opsomming zijn A, B en M punten en zijn k en l lijnen. De verzameling van de punten P waarvoor geldt • d(P, A) = d(P, B) is de middelloodlijn van het lijnstuk AB • d(P, k) = d(P, l) is het bissectricepaar van k en l als k en l snijdende lijnen zijn • d(P, k) = d(P, l) is de middenparallel van k en l als k en l evenwijdige lijnen zijn • d(P, M) = r is de cirkel met middelpunt M en straal r 12. 3

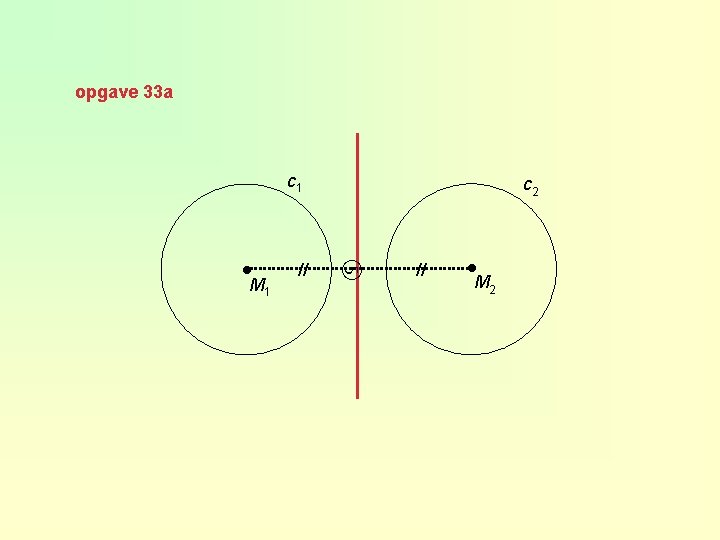
opgave 33 a c 1 // ● M 1 c 2 // ● M 2

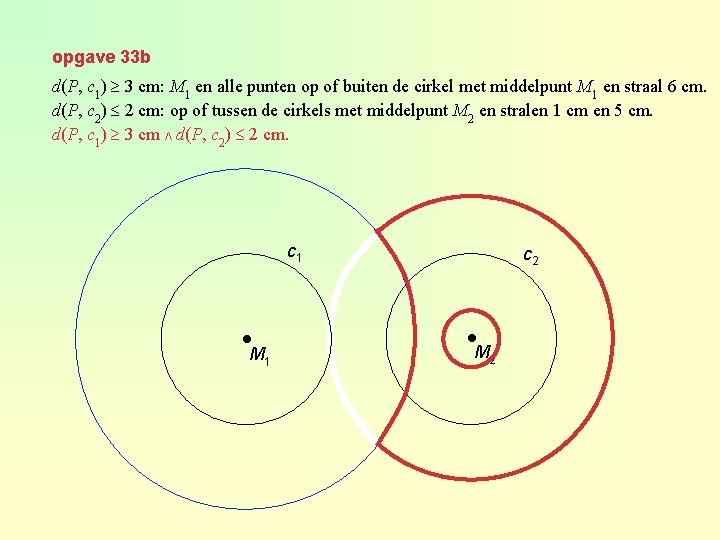
opgave 33 b d(P, c 1) ≥ 3 cm: M 1 en alle punten op of buiten de cirkel met middelpunt M 1 en straal 6 cm. d(P, c 2) ≤ 2 cm: op of tussen de cirkels met middelpunt M 2 en stralen 1 cm en 5 cm. d(P, c 1) ≥ 3 cm ∧ d(P, c 2) ≤ 2 cm. c 1 ● M 1 c 2 ● M 2

De parabool als meetkundige plaats Het punt F heet het brandpunt van de parabool en de lijn l heet de richtlijn van de parabool. Definitie van de parabool: Een parabool is de verzameling van alle punten met gelijke afstanden tot een lijn en een punt dat niet op die lijn ligt. d(P, F) = d(P, l) Werkschema: het tekenen van punt P van parabool met brandpunt F en richtlijn l. 1. Teken een punt V op l. 2. Teken door V de loodlijn k op l. 3. Teken de middelloodlijn m van het lijnstuk FV. 4. Het snijpunt van k en m is het punt P. 12. 3

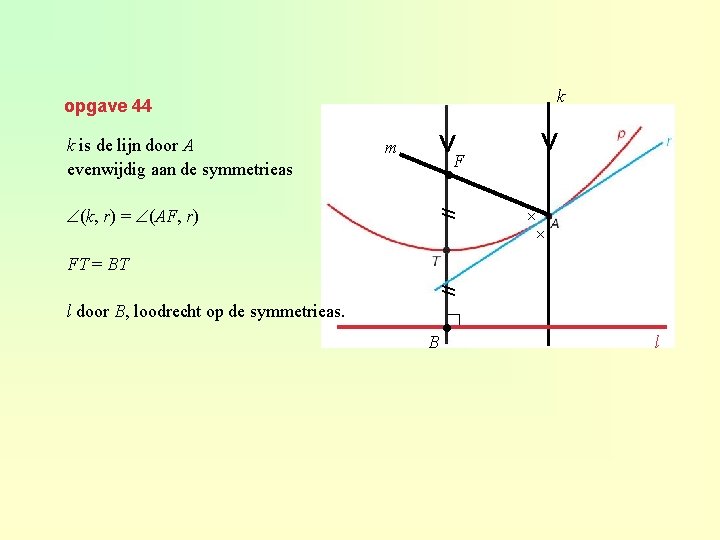
k opgave 44 (k, r) = (AF, r) V m F ● // k is de lijn door A evenwijdig aan de symmetrieas V × × // FT = BT l door B, loodrecht op de symmetrieas. ∟ B ● l