Omega Notation Theta Notation Selection Sort 1 Omega

Omega Notation Theta Notation & Selection Sort 1

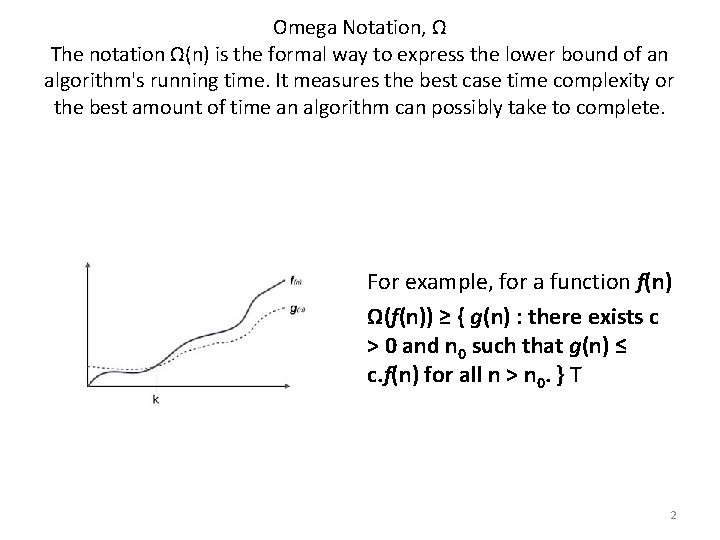
Omega Notation, Ω The notation Ω(n) is the formal way to express the lower bound of an algorithm's running time. It measures the best case time complexity or the best amount of time an algorithm can possibly take to complete. For example, for a function f(n) Ω(f(n)) ≥ { g(n) : there exists c > 0 and n 0 such that g(n) ≤ c. f(n) for all n > n 0. } T 2

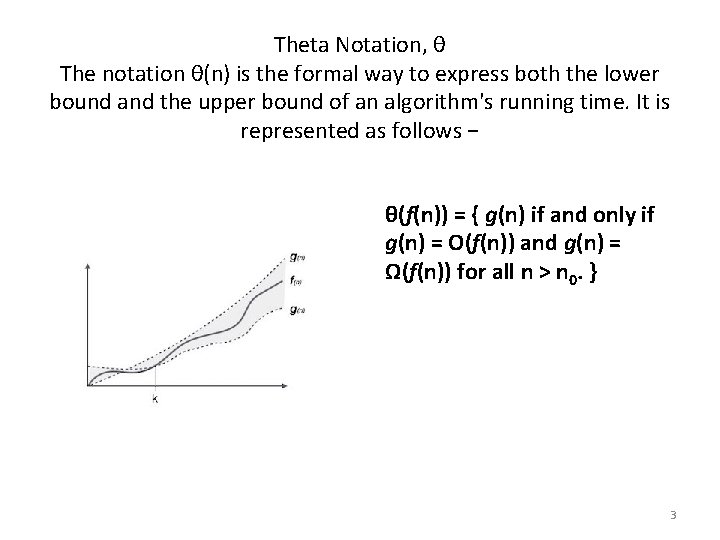
Theta Notation, θ The notation θ(n) is the formal way to express both the lower bound and the upper bound of an algorithm's running time. It is represented as follows − θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n 0. } 3

Common Asymptotic Notations constant − Ο(1) logarithmic − Ο(log n) linear − Ο(n) n log n − Ο(n log n) quadratic − Ο(n 2) cubic − Ο(n 3) polynomial − nΟ(1) exponential − 2Ο(n) 4

How Selection Sort work • Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list. • The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right. • This algorithm is not suitable for large data sets as its average and worst case complexities are of Ο(n 2), where n is the number of items. 5

Algorithm • Step 1 − Set MIN to location 0 • Step 2 − Search the minimum element in the list • Step 3 − Swap with value at location MIN • Step 4 − Increment MIN to point to next element • Step 5 − Repeat until list is sorted 6

Algorithm • • • Worst Case Time Complexity [ Big-O ]: O(n 2) Best Case Time Complexity [Big-omega]: O(n 2) Average Time Complexity [Big-theta]: O(n 2) Space Complexity: O(1) 7