Oleh Erviningsih s MTs N Plandi Jombang MACAM

Oleh Erviningsih s MTs. N Plandi Jombang

MACAM – MACAM HIMPUNAN A. Himpunan Bilangan 1. Himpunan bilangan asli ; A = { 1, 2, 3, 4, 5, 6, 7, . . } 2. Himpunan bilangan cacah ; C = { 0, 1, 2, 3, 4, 5, 6, 7, . . } 3. Himpunan bilangan ganjil ; J = {1, 3, 5, 7, 9, 11, 13, . . }

4. Himpunan bilangan genap ; G = { 2, 4, 6, 8, 10, 12, 14, . . } 5. Himpunan bilangan prima ; P = { 2, 3, 5, 7, 11, 13, . . } 6. Himpunan bilangan kuadrat ; K = {1, 4, 9, 16, 25, 36, 49, . . }

B. Himpunan Kosong Merupakan himpunan yang memiliki anggota, ditulis : { } atau 0. Contoh; 1. Himpunan hewan berkaki 5 2. Himpunan siswa MTs. N yang beragama kristen

C. Himpunan Terhingga Merupakan himpunan yang memiliki banyak anggota terbatas. Contoh : A adalah himp bilangan asli kurang dari 100 A = { 1, 2, 3, 4, 5, . . . 99 } B adalah himp bilangan prima kurang dari 25 B = { 2, 3, 5, 7, 11, 13, 17. 19, 23 }

D. Himpunan Tak Hingga Merupakan himpunan yang memiliki banyak anggota tak terbatas. Contoh : A adalah himpunan bilangan asli lebih dari 8 A = { 9, 10, 11, 12, . . . } B adalah himpunan bilangan prima lebih dari 7 B = { 11, 13, 17, 19 , . . . }

HIMPUNAN SEMESTA Himpunan semesta dari suatu himpunan ialah himpunan yang memuat semua anggota yang terdapat suatu himpunan, dan himpunan semesta diberi lambang ; S

MENYATAKAN SUATU HIMPUNAN Suatu himpunan dapat dinyatakan dengan : a. kata-kata ( metode deskripsi ) A = { bilangan prima kurang 10 } B = { faktor dari 12 } C = { bilangan ganjil kurang dari 11 }

b. notasi pembentuk komponen ( metode rule ) Contoh: A = { x | x bil. prima kurang dari 10 } B = { x | x faktor dari 12 } C = { x | x bil. ganjil kurang dari 11 }

c. mendaftar anggotanya ( metode Roster ) A = { 2, 3, 5, 7 } B = { 1, 2, 3, 4, 6, 12 } C = { 1, 3, 5, 7, 9 }

GABUNGAN HIMPUNAN Gabungan himpunan A dan B adalah suatu himpunan yang anggota-anggota nya menjadi anggota A saja atau anggota B saja atau anggota persekutuan A dan B.

Dengan notasi pembentuk himpunan, gabungan himpunan A dan B didefinisikan sebagai : A B = { x | x A dan x B }.

Contoh Soal A = { m, e, r, a, h } B = { r, a, t, i, h } A B =. . . Penyelesaian : Semua anggota A dan B, tetapi anggota yang sama hanya di tulis satu kali. A B = { m, e, r, a, h, i, t }

DIAGRAM VENN Diagram Venn merupakan gambar himpunan yang digunakan untuk menyatakan hubungan beberapa himpunan.

S A

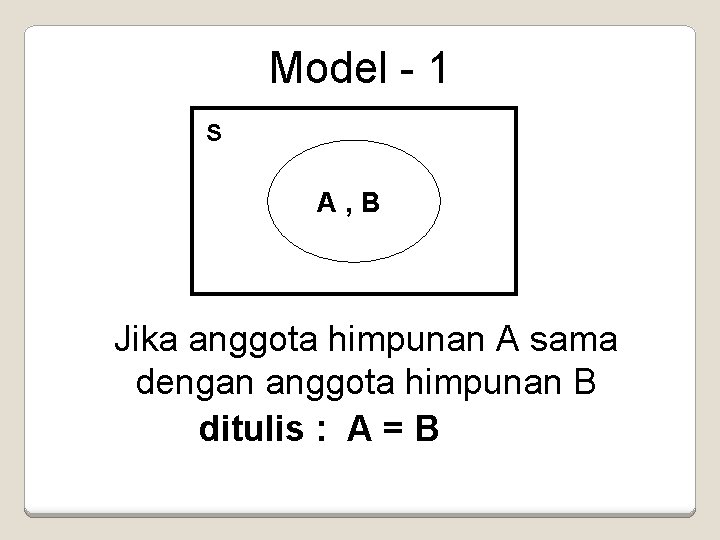
Model - 1 S A, B Jika anggota himpunan A sama dengan anggota himpunan B ditulis : A = B

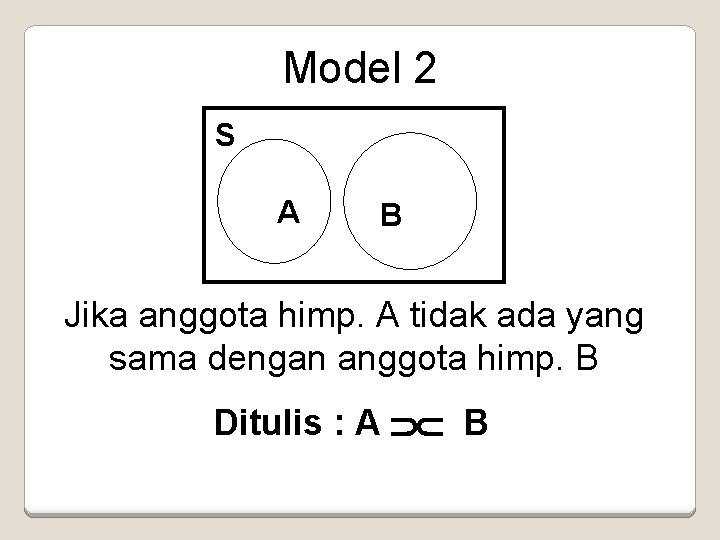
Model 2 S A B Jika anggota himp. A tidak ada yang sama dengan anggota himp. B Ditulis : A B

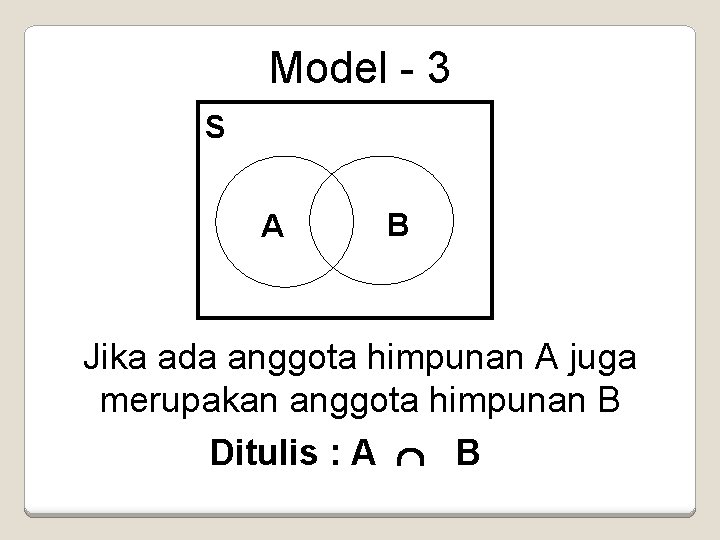
Model - 3 S A B Jika ada anggota himpunan A juga merupakan anggota himpunan B Ditulis : A B

Model 4 S A B Jika semua anggota himpunan B adalah anggota himpunan B Dtulis : B A

LATIHAN -1 S = { bilangan asli }, A = { bilangan ganjil } B = { bilangan prima > 2 }, himpunan di atas dapat dinyatakan dalam diagram Venn berikut :

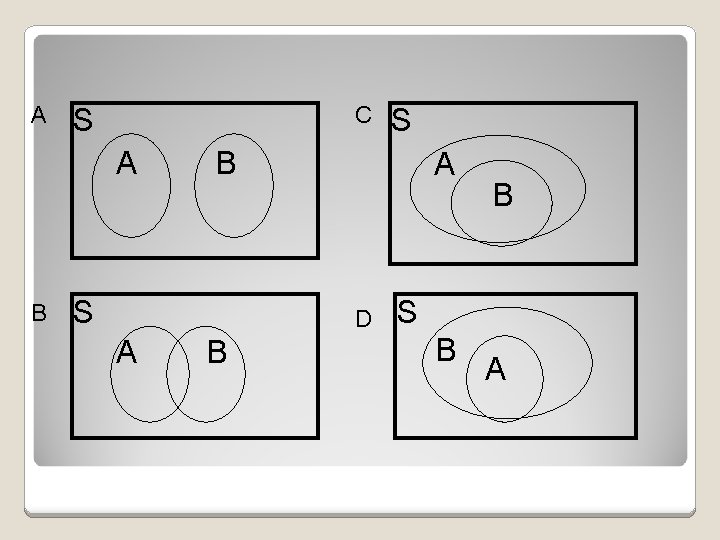
A C S A B B S A D A S B B S B A

Pembahasan S = { 1, 2, 3, 4, 5, . . . } A = { 1, 3, 5, 7, 11, . . . } B = { 3, 5, 7, 11, . . . } Karena semua anggota himpunan B dimuat di A maka B A, artinya kurva B ada di dalam kurva A. Jadi jawaban yang benar adalah : C

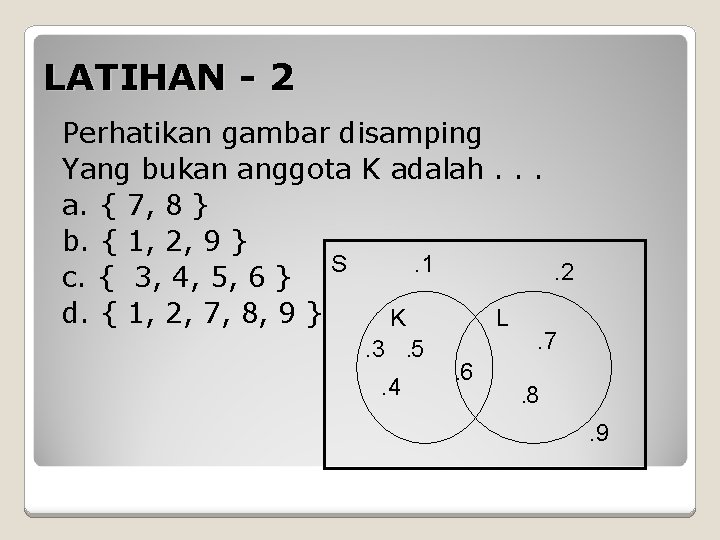
LATIHAN - 2 Perhatikan gambar disamping Yang bukan anggota K adalah. . . a. { 7, 8 } b. { 1, 2, 9 }. 1 S. 2 c. { 3, 4, 5, 6 } d. { 1, 2, 7, 8, 9 } K L. 3. 4 . 5 . 7 . 6 . 8 . 9

Pembahasan S = { 1, 2, 3, . . . , 9 S}. 1. 2 K = { 3, 4, 5, 6 } K L Anggota S yang tidak. 3. 5. 7. 6 menjadi anggota K. 4. 8 adalah : { 1, 2, 7, 8, 9 } Jadi jawaban yang benar adalah : D. 9

Pembahasan K = { k, o, m, p, a, s } L = { m, a, s, u, k } K L = { k, o, m, p, a, s, u } Diantara jawaban A, B, C, dan D yang memiliki anggota = anggota K L adalah A Jadi jawaban yang benar : A

LATIHAN - 4 P = { faktor dari 10 } Q = { tiga bilangan prima pertama } P Q=. . a. { 1, 2, 3, 4, 5, 7, 10 } b. { 1, 2, 3, 4, 5, 10 } c. { 1, 2, 3, 5, 7, 10 } d. { 1, 2, 3, 5, 10 }

Pembahasan P = { 1, 2, 5, 10 } Q = { 2, 3, 5 }, maka : P Q = { 1, 2, 3, 5, 10 } Jadi jawaban yang benar adalah : D

LATIHAN - 5 Jika himpunan A B dengan n(A) = 11 dan n(B) = 18, maka n ( A B ) =. . . a. 7 c. 18 b. 11 d. 28

Pembahasan n ( A ) = 11 n ( B ) = 18 Setiap A B, maka A B = A Sehingga n ( A B ) = n ( A ) n ( A B ) = 11 Jadi jawaban yang benar adalah : B

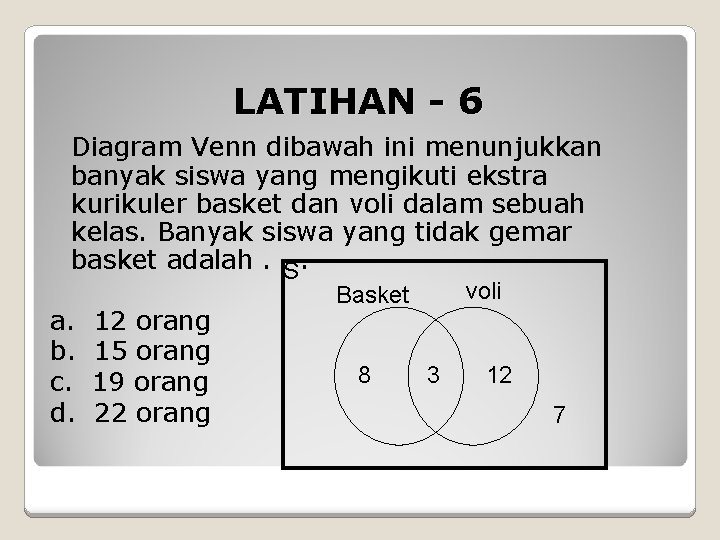
LATIHAN - 6 Diagram Venn dibawah ini menunjukkan banyak siswa yang mengikuti ekstra kurikuler basket dan voli dalam sebuah kelas. Banyak siswa yang tidak gemar basket adalah. . S. a. b. c. d. 12 orang 15 orang 19 orang 22 orang voli Basket 8 3 12 7

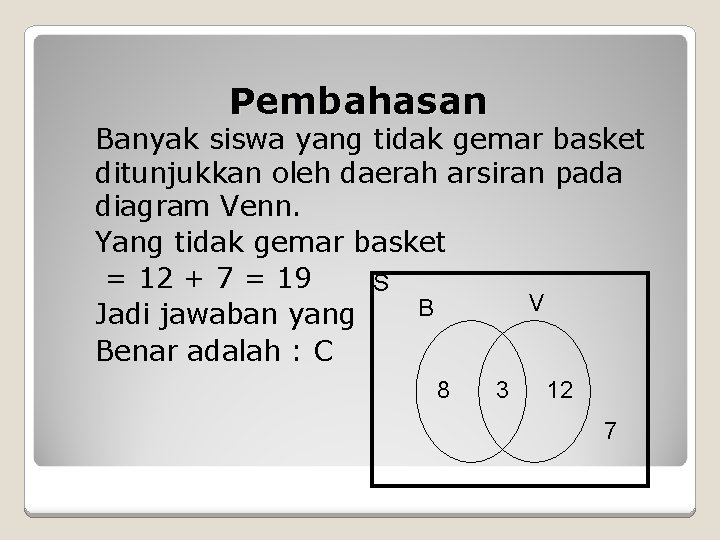
Pembahasan Banyak siswa yang tidak gemar basket ditunjukkan oleh daerah arsiran pada diagram Venn. Yang tidak gemar basket = 12 + 7 = 19 S V B Jadi jawaban yang Benar adalah : C 8 3 12 7

LATIHAN - 7 Dalam sebuah kelas terdapat 17 siswa gemar matematika, 15 siswa gemar fisika, 8 siswa gemar keduanya. Banyak siswa dalam kelas adalah. . . a. 16 siswa c. 32 siswa b. 24 siswa d. 40 siswa

Pembahasan n(M) = 17 orang n(F) = 15 orang n(M F ) = 8 orang n( M F ) = n(M) + n(F) – n(M F ) = 17 + 15 – 8 = 32 – 8 = 24 orang Jadi jawaban yang benar adalah : B

LATIHAN - 8 Dalam seleksi penerima beasiswa, setiap siswa harus lulus tes matematika dan bahasa. Dari 180 peserta terdapat 103 orang dinyatakan lulus tes matematika dan 142 orang lulus tes bahasa.

Banyak siswa yang dinyatakan lulus sebagai penerima beasiswa ada. . . a. 38 orang b. 45 orang c. 65 orang d. 77 orang

Pembahasan n(S) = 180 orang n(M) = 103 orang n(B) = 142 orang n(M B ) = x orang n(S) = n( M B ) = n(M) + n(B) – n( M B) 180 = 103 + 142 - X X = 245 – 180 = 65 Jadi yang lulus adalah 65 orang = ( C )

LATIHAN-9 Dalam satu kelas terdapat 40 siswa, 12 orang di antaranya senang biola, 32 orang senang gitar, dan 10 orang senang keduanya. Banyak siswa yang tidak senang keduanya adalah…. a. 2 orang b. c. 6 orang b. 4 orang d. 8 orang

Pembahasan Biola = 12 orang, Gitar = 32 orang Biola dan Gitar = 10 orang. Jlh Siswa di kelas = 40 orang. Jlh siswa = n(B) +n(G) – n( B G) 40 – x = 12 + 32 - 10 40 - x = 44 - 10 x = 40 – 34 = 6

LATIHAN - 10 Sebuah RS mempunyai pasien sebanyak 53 orang, 26 orang menderita demam ber - arah, dan 32 orang menderita muntaber. penderita DBD dan muntaber 7 orang, yang tidak menderita DBD atau muntaber adalah … a. 2 orang c. 5 orang b. 3 orang d. 6 orang

Pembahasan Jumlah pasien = 53 orang. Demam berdarah = 26 orang. Muntaber = 32 orang. DBD dan muntaber = 7 orang. Bkn DBD atau muntaber = X orang. X = ( 53 org ) - ( 26 org + 32 org – 7 ) = X = 53 org – 51 org X = 2 orang

LATIHAN - 11 Dari 40 orang anak, ternyata 24 anak gemar minum teh, 18 anak gemar minum kopi, 5 anak tidak gemar minum keduanya Banyaknya anak yang gemar keduanya adalah. . . a. 2 orang b. 5 orang c. 7 orang d. 9 orang

Pembahasan Jumlah anak = 40 orang Teh = 24 orang Kopi = 18 orang Teh dan Kopi = x orang Tidak keduanya = 5 orang (24 + 18 ) - x = 40 - 5 42 - x = 35 x = 42 - 35 = 7 Yang gemar keduanya adalah 7 anak.

LATIHAN - 12 Dari 60 orang siswa ternyata 36 orang gemar membaca, 34 orang gemar menulis, 12 orang gemar kedua-duanya. Banyaknya anak yang tidak mengemari keduanya adalah. . . a. 2 orang b. 5 orang c. 7 orang d. 9 orang

Pembahasan Jumlah anak = 60 orang Membaca = 36 orang Menulis = 34 orang Membaca dan menulis = 12 orang Tidak keduanya = x orang (36 + 34 ) - 12 = 60 - x 58 = 60 - x x = 60 – 58 x = 2.

LATIHAN - 13 Jika himpunan B A dengan n(A) = 25 dan n(B) = 17, maka n ( A B ) =. . . a. 8 c. 17 b. 11 d. 25

Pembahasan n ( A ) = 25 n ( B ) = 17 Setiap B A, maka A B = A Sehingga n ( A B ) = n ( A ) n ( A B ) = 25

LATIHAN - 14 Dalam sebuah kelas terdapat 20 siswa gemar matematika, 15 siswa gemar fisika, 8 siswa gemar keduanya. Banyak siswa dalam kelas adalah. . a. 23 siswa b. c. 28 siswa b. 27 siswa d. 43 siswa

Pembahasan n(M) = 20 orang n(F) = 15 orang n(M F ) = 8 orang n( M F ) = n(M) + n(F) – n(M F ) = 20 + 15 – 8 = 35 – 8 = 27 orang