OLASILIK KONUSU RENCLERE NEDEN ZOR GELMEKTEDR Giri Olaslklar

OLASILIK KONUSU ÖĞRENCİLERE NEDEN ZOR GELMEKTEDİR?

Giriş Olasılıkları Tahmin Etme ve Değerlendirme Olası Durumları Belirleme Olasılıkla İlgili Temel kavramları Anlama ve Uygulama Olasılık Çeşitlerini ve Aralarındaki İlişkiyi Anlama Teknoloji Destekli Olasılık Öğretimi Sonuç

GİRİŞ Öğrenciler matematiğin diğer konularında olduğu gibi olasılık kavramıyla ilgili kendi deneyimlerinden edindikleri, zihinlerinde yerleşmiş fikirlerle sınıfa gelirler. Çocukluktan itibaren herhangi sistematik bir eğitim almadan var olan bu sezgilerin, öğrencilerin olasılık kavramının gelişiminde önemli rol oynadığı belirtilmektedir.

Ülkemizde uygulanmaya başlayan yeni matematik öğretim programlarında ilköğretim 4. sınıftan itibaren öğrenilmeye başlayan olasılık kavramlarının öğrencilerin günlük hayatta karşılaştıkları temel olasılık olguları üzerine yapılandırılmasının ve dolayısıyla sezgiye dayalı olarak geliştirilmesinin önemi vurgulanmaktadır. Çeşitli araştırmalar sezgilerin çoğunlukla yanıltıcı olduğunu ve öğrencilerde kavram yanılgılarına yol açtığı belirtmişlerdir. Bunlar da öğrencilerin olasılık kavramını öğrenmede zorluk çekmelerine sebep olmaktadır. Bu bölümde ilköğretim seviyesindeki olasılık öğrenimi ve öğretimi üzerine odaklanacaktır.

Bölümün geri kalan kısmında literatürde belirtilen olasılıkla ilgili kavram yanılgıları ve öğrenme zorlukları ilköğretim müfredatındaki konular esas alınarak şu dört ana başlık altında ele alınacaktır : * Olasılıkları tahmin etme ve değerlendirme * Olası durumları belirleme * Olasılıkla ilgili temel kavramları anlama ve uygulama * Olasılık çeşitlerini anlama ve aralarındaki ilişkiyi anlama Daha sonra öğrencilerin olasılığa ilişkin kavramsal anlamalarının ve akıl yürütmelerinin geliştirilmesine yönelik uygulamalara değinilecek ve bir örnekle detaylı olarak incelenecektir.

OLASıLıKLARı TAHMIN ETME VE DEĞERLENDIRME Hem günlük yaşamı yakından ilgilendiren alanlarda hem de bilimin çeşitli dallarında olasılık, belirsizlik durumlarıyla ilgili kararlar verme sürecinde önemli rol oynar. Mesela her gün medya aracılığıyla , “İstatiksel olarak uçak yolculuklarında kaza riski 0, 000004 olarak belirtilmiştir” yada “Florida da ki ev sahiplerinin dikkatine ! Uzmanlara göre önümüzdeki yıl Florida kıyılarını vurabilecek bir kasırganın olma olasılığı %49 olarak bekleniyor” gibi olasılık içeren çok çeşitli ifadeler duyarız ve bunları yorumlarız. Yapılan araştırmalar bu tür durumlarda insanların olasılık kuramı ilkeleriyle bağdaşmayan bir takım sezgilerle düşünme eğiliminde olduklarını göstermiştir.

Mesela bir hava durumu spikerinin “yarın %70 yağmur yağma olasılığı vardır” ifadesinden öğrencilerin ne anlam çıkardıkları sorulduğunda , bazı öğrencilerin “ %70 yağmur yağma olasılığını “ daha kesin bir nitel ifadeye çevirerek “ yağmur yağacaktır “ şeklinde bir tahminde bulundukları görülmüştür. Konold öğrencilerin genellikle bu çeviriyi yaparken %0 - %100 ihtimal aralığında %0 ı “ hayır “ %100 “evet “ ve ‘’ % 50 bilmiyorum’’ anlamında kullandıklarını belirtmiştir. Öğrencilerin tahmin ederken o olayın olup olmayacacığını “evet” ya da bazen “bilmiyorum ”şeklinde ifade etme eğiliminde olduklarına ortaya koymuştur ve bunu “sonuç yaklaşımı” olarak adlandırmıştır.

Konold Sonuç Yaklaşımını belli başlı özelliklerini şöyle sıralamıştır. 1) Olasılığın tek bir denemenin sonucunu tahmin etmek olarak yorumlama ve bu nedenle tek denemeden sonra olasılığı doğru yada yanlış olarak değerlendirme. 2) Olasılık tahminlerini nedensel açıklamalara dayanarak yapma.

Bir diğer sıkça karşılan hata ise problemdeki verileri teslim eden sayıların çarpılmasıdır.

Öğrencilerin olasılıkla ilgili muhakemelerini inceleyen diğer bazı araştırmacılar öğrencilerin olasılık problemlerini çözerken yaygın olarak kullandığı bir takım stratejiler olduğunu saptamışlardır. Kahneman , Tversky’nin Literatüre katmış oldukları “Temsil Kısa yolu” bunlardan biridir. Temsil kısa yoluna göre, bir olayın olma olasılığı, o olayın örnek uzayı ya da rastgele meydana gelme sürecini en iyi şekilde yansımasına dayalı olarak değerlendirilir. Örneğin, temsil kısa yolu kullanımından kaynaklanan bir yanılgıya sahip bir öğrenci, altı çocuklu ailelerde kız (K) ve erkek (E) çocukların doğuş sırasına bakarak EEEEEE sıralanmasının KEKKEE sıralamasına göre daha az olası olduğunu düşünebilmektedir. Oysa teorik olarak iki sıralamada eş olasılıdır. Çünkü doğacak çocuğun kız ya da erkek olma olasılığı ½ ya da %50 olduğuna göre altılı her bir sıralamanın olasılıklarını 1/64 yani 64 farklı sıralamanın her birinin olma olasılığı birbirine eşittir.

Öğrencilerin sezgilere dayanan kavram yanılgılarının yaşla ( 5, 7, 9, 11. sınıflar ve üniversite ) değişiminin araştırıldığı bir çalışmada Fischbeni ve Schnarch temsil kısa yoluna başvurabilecek aşağıdaki gibi bir soruyla öğrencilerin yanıtlamalarını incelemişlerdir: Bir şans oyununda 40 sayı arasında ( 1 -40 ) 6 sayı seçilmektedir aşağıdaki seçimlerden hangisinin kazanma olasılığı daha yüksektir? 1 -2 -3 -4 -5 -6 39 -1 -17 -33 -8 -27 Fiscbein ve Schnarch bu soruda temsil kısa yolundan kaynaklanan yanılgının yaşla birlikte azaldığını tespit etmiştir. Cevap yüzdelerine bakıldığında örneğin, 5 ve 7. sınıf öğrencilerinin büyük çoğunluğunun (%70 ve %50) “ 39 -1 -17 -33 -8 -27” seçiminin kazanmasını daha olası buldukları görülmektedir.

Fischbein ve Schnarch öğrencilere yine temsil kısa yoluyla ilgili olan aşağıdaki gibi bir olasılık tahmin sorusu sormuşlardır Bir bozuk para üç kez havaya atıldığında, ardına üç kez tura ( TTT ) geldikten sonra dördüncünün de tura ( T ) gelme olasılığı nedir?

Soruya verilen cevapların analizi hem 5. hem de 6. sınıf öğrencilerinin %35’ inin TTT’ den sonra tekrar tura ( T ) gelme olasılığının yazı gelme olasılığında daha düşük olduğunu düşündüklerini ortaya çıkarmıştır. Oldukça fazla sayıda öğrencinin verdiği bu yanıt ‘’ kumarcı yanılgısı ‘’ olarak da bilinen “olumsuz sonralık etkisi” kavram yanılgısını içermektedir. Bu da öğrencilerin henüz rastgele bir sürecin ardışık çıktılarının bağımsız olduğuna dair bir düşünce sahip olmadığını göstermektedir. Fischbein ve Schnarch’ in çalışmasından verilen bu iki örnekte (şans oyunu ve yazı-tura tahminleri) öğrencilerin aşağı yukarı yarısının (5. sınıf: %40 ve 7. sınıf: %55) doğru cevabı verdikleri görülmektedir.

OLASI DURUMLARI BELİRLEME Bir olasılık durumu verildiğinde olası durumları belirlemede kombinasyonel düşünme ve problem çözme becerisi önemli bir rol oynar. Piaget ve Inhelder 4 -12 yaşlarındaki çocuklarla yaptıkları çalışmaların sonucunda olasılık kavramının gelişiminin temelinde diziliş, permütasyon ve kombinasyonda oluşan kombinasyonel işlemler ile örnek uzayın kavranması ve oran olgusunun anlaşılması olduğunu belirtmişlerdir. Bu konuda yapılan araştırmalara bakıldığında ilköğretimden ortaöğretime kadar öğrencilerin kombinasyonel işlemleri anlama ve ilgili problemleri çözmede zorlandıkları görülmektedir. Örneğin Fischbein ve Gazit’in 6. ve 8. sınıflardan 84 öğrenci ile yaptıkları çalışmada, çözümünde farklı kombinasyonel işlemlerin kullanılmasını gerektiren problemlerde öğrencilerin yaptıkları hatalar incelenmiştir. Bu problemlerin içerdikleri 4 ayrı kombinasyonel işlem aşağıdaki gibidir.

TEKRARLI DİZİLİŞ TEKRARSIZ DİZİLİŞ PERMÜTASYON KOMBİNASYON

Fischbein ve Gazit’in çalışmasında 6 ve 8. sınıf öğrencilerinin permütasyon ve diziliş problemlerindeki başarılı kombinasyon problemlerine göre daha yüksek olmuştur. Fakat bu tür problemlerin çözümünde sistematik hatalar saptanmıştır. Bundan en çok rastlananı yanlış kombinasyonel işlem formülünün kullanılmasıdır.

Bir diğer sıkça karşılan hata problemdeki verileri temsil eden sayıların çarpılmasıdır. Örneğin, n=4 elemanlı bir kümeden elde edilen r=2 elemanlı grupların sayısını hesaplarken öğrenci “C(4, 2)=4 x 3/2=6 yerine C=4 x 2 yazmaktadır. Burada ise öğrenci verilen probleme uygun kombinasyon işlemini uygulayamamaktadır ancak Fischbeni ve Gazit bu örnekteki her iki çözüm yolunun da aynı yanıta götürdüğü durumların olduğuna da dikkat çekmişlerdir. Mesela n=3 ve r=2 durumunda doğru cevap “ 3 x 2” olup iki yolla da ulaşmaktadır. Öğrencinin bu gibi durumlarda sonuca kombinasyonel muhakeme ile mi yoksa rastlantı eseri olarak mı ulaştığının anlaşılması Fischbein ve Gazit’in yaptıkları gibi öğrencinin benzer başka bir probleme verdiği yanıtlar incelenmelidir.

Olasılıkla İlgili Temel Kavramları Anlama ve Uygulama 6. sınıfa kadarki ilköğretim matematik müfredatında, olasılık konularının öğretiminde öğrencilerin sezgisel olasılık tahminlerinin esas alındığı bir yaklaşım öngörülmektedir. 6. sınıftan itibaren ise olasılık konularının eğitiminde sezgisel olasılık tahminlerinden olasılık hesaplamalarına geçiş söz konusudur ve bu geçişin sağlıklı bir şekilde olması öğrencilerin temel olasılık kavramlarını anlama ve anlamlandırmalarını zorunlu kılmaktadır.

Bu temel kavramlardan özellikle “eş olasılıklı olma” ve “örnek uzay” ın anlamlandırılmasında öğrencilerin güçlük çektiği görülmektedir. “Eş olasılıklı olma” kavramı, bir olayın olma olasılığı hesaplanırken o olayın sonuçlarının her birinin olma olasılıklarının eşit olma prensibine dayanır örneğin, tek zar atışında hilesiz zarın simetri özelliğine dayanarak her bir yüzeyin(1, 2, 3, 4, 5, 6) gelme olasılıklarının birbirine eşit ve 1/6 olduğunu söyleyebiliriz.

Ancak öğrencilerin olayların “eş olasılıklı olma” özelliğini aşırı genelleme ile yanlış durumlara da uyguladıkları görülmektedir. Öğrencilerin rastgele olayların tüm olası çıktılarını doğal olarak eşit olasılıklı görme eğilimleri literatürde “eşit olasılık yanlılığı” olarak ifade edilmektedir.

Örneğin Lecoutre ve meslektaşları, öğrencilere iki zar aynı anda atıldığında üste gelen sayıların toplamının 9 veya 11 gelme olasılıkları nedir diye bir soru yönelttiğinde, öğrencilerin bu soruya karşılık olarak 9 veya 11 gelme olasılıklarının eşit olacağı yönünde yorum yaptıklarını gözlemişlerdir. Burada öğrencilerin zar atıldığında kaç geleceğini şansa bağlı olacağını düşünerek iki zarın toplamının 9 veya 11 gelme olasılıklarının eşit olacağına inandıkları görülmektedir. Yani öğrenciler herhangi bir rastgele olayın doğal olarak şansa bağlı olduğunu ve bunun sonucu olarak da eşit olasılıklı olduğunu düşünmektedirler.

Yukarıdaki iki zarın toplamlarının gelme olasılıklarının karşılaştırıldığı örnekte de olduğu gibi, öğrencilerin olasılık tahminlerinde örnek uzayı oluşturmada zorlandığı görülmektedir. Bundan dolayı özellikle iki veya daha çok basit olayın ardına veya birlikte meydana geldiği bileşik olaylarda, öğrencilerin olasılık tahminlerinde yanılgıya düştükleri görülmüştür. Çünkü bu tür durumlarda ya bileşik olayı meydana getiren basit olayın olası sonuçlarının eş olasılıklı olması aşırı genellenerek o bileşik olayın da sonuçlarının eş olasılıklı olduğu düşünülüyor yada bileşik olayın tüm olası sonuçlarının farkına varılamıyor veya tam olarak oluşturulamıyor

Bu konuda yapılan araştırmalarda Fischbein ve Gazit on iki ders boyunca olasılık konularını öğrenen öğrencilere, bir zar atıldığında 3 veya 6 gelme olasılığını sorduklarında, verilen doğru cevap yüzdeleri sınıflara göre, sırasıyla, %32. 4 %62. 5 %86. 5 bulunmuştur. Ancak öğrencilerden örnek uzayının açıkça belirtilmediği birleşik olayların olma olasılıklarını hesaplamalarını istendiğinde doğru cevap verme yüzdeleri oldukça düşmüştür.

Örneğin, iki zar atıldığında zarların toplamının 6 gelme olasılığı sorulduğunda, 6. sınıf öğrencilerinin sadece %11. 3’ ü ve 7. sınıf öğrencilerinin ise sadece %51. 9’ u doğru yanıt verebilmişlerdir. Bu ani değişimin öğrencilerin örnek uzayın eleman sayısını 36(6× 6) yerine 12 (6+6) diye düşünmelerinden kaynaklandığı saptanmıştır.

Bir başka çalışmada ise Shaughnessy ve Ciancetta ABD’ de uygulanan ulusal bir ölçme ve değerlendirme sınavında 12. sınıf öğrencilerinin çok az bir kısmının doğru cevap verebildiği bir bileşik olayın olma olasılığı ile ilgili aşağıdaki soruyla çeşitli sınıf seviyelerinden öğrencilerin yanıtlarını incelemişlerdir.

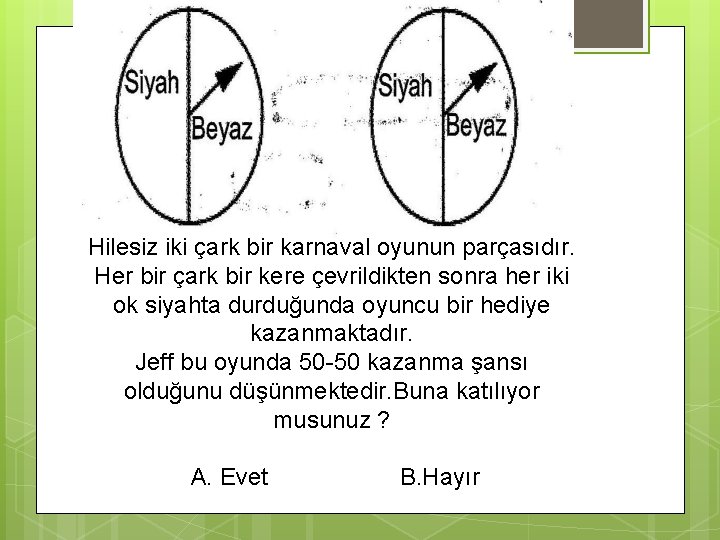
Hilesiz iki çark bir karnaval oyunun parçasıdır. Her bir çark bir kere çevrildikten sonra her iki ok siyahta durduğunda oyuncu bir hediye kazanmaktadır. Jeff bu oyunda 50 -50 kazanma şansı olduğunu düşünmektedir. Buna katılıyor musunuz ? A. Evet B. Hayır

Yapılan anketin sonuçları öğrencilerin çoğunun oyunu kazanma şansının “ 50 -50” olduğuna inandıklarını göstermiştir. Yalnızca 6 ve 7. sınıf öğrencilerinin %19’ u ile 8. sınıf öğrencilerinin ise %24’ ü doğru ya da kısmen doğru açıklamalı yanıt verebilmiştir. Halbuki bu bileşik olayın örnek uzayını listelemek oldukça basittir ve buradan da siyah ve siyah gelme olasılığının %25 ya da ¼ olduğu çok kolay bir şekilde görülmektedir.

Ancak yanlış yanıtı veren öğrenciler örnek uzayı düşünmeden hareket edip “ 50 -50” kazanma şansını her bir çarkın eşit olarak yarısının siyah yarısının beyaz olmasına bağlamışlardır. Bunun yanı sıra deneyin olası çıktılarını yani örnek uzayını düşünerek cevap verenlerden oyuna kazanma olasılığının “ 1/3” olduğu sonucuna varan öğrenciler de olmuştur. Bu öğrencilerin deneyin olası çıktılarını “SS, BB, SB, ” (S=Siyah, B=Beyaz) olarak düşündükleri belirlenmiştir. Buradaki yaygın yanılgı ise SB ve BS çıktılarının ayırt edilmemesidir.

OLASILIK ÇEŞİTLERİNİ VE ARALARINDAKİ İLİŞKİYİ ANLAMA İlköğretim matematik öğretim programının 8. sınıfında ele alınan teorik, deneysel ve öznel olasılık çeşitleri aslında olasılığın tarihi gelişiminde ön plana çıkan ve olasılıksal olguların yorumlanmasında kullanılan üç temel olasılık kuramı Klasik olasılık kuramı Olasılık sıklık kuramı Öznel olasılık kuramı

Olası durumları belirlemede kullanılan sayma yöntemleri ve teorik olasılık , klasik olasılık kuramına dayanır. Olasılığın klasik tanımı : Bir olayın olası tüm çıktıları eşit olasılıklı olduğundan o olayla ilgili istenen durumların sayısının tüm olası durumların toplam sayısına oranıdır. Örneğin : Hilesiz bir zarın simetrik altı yüzeyi olduğundan her bir yüzeyin gelme olasılıkları eşit olarak kabul edildikten sonra bir zar atıldığında çift sayı gelme olasılığı , istenen olayın eleman sayısının , s (2, 4, 6)=3 , tüm olası çıktıların toplam sayısının , s (1, 2, 3, 4, 5, 6) =6 , oranıdır, yani 3/6 = ½ dir.

Eğer bir deneydeki her bir çıktının meydana gelme olasılıkları eşit değilse klasik olasılık kuramı uygulanamaz deneysel olasılığın dayandığı olasılık sıklık kuramına göre ise olasılık , aynı koşullarda çok sayıda tekrarlanan bağımsız denemelerin sonucunda olayın gerçekleştiği göreli sıklığın limiti olarak tanımlanmaktadır. Örneğin, hilesiz bir bozuk paranın havaya atılışını ele alırsak , bu süreç birbirinden bağımsız denemelerde aynı koşullar altında tekrar yinelenebilir.

Öznel olasılık ise bir olayın olasılığını kişilerin inanış derecesine göre belirlediği öznel olasılık kuramından ortaya çıkmıştır. Örneğin, bir basketbol taraftarı şöyle söyleyebilir : “Efes’ in Avrupa basketbol Ligi şampiyonu olma olasılığının %90 olduğuna inanıyorum çünkü bu yıl gerçekten çok güzel oynuyorlar. ” Yani öznel olasılık belirli bir takım hesaplamalara değil de daha çok akla yatkınlık değerlendirmesine ya da kişinin deneyimlerine dayanarak belirlenmektedir.

Büyük Sayılar Kanunu Hilesiz bir madeni paranın atılması deneyinde , deneysel veri toplamak için para 10 kez havaya atıldığında 7 yazı 3 tura veya 1 yazı 9 tura gelebilir. Ama eğer parayı 10000 kez havaya atarsak , yazı ve turanın geliş yüzdeleri teorik olasılıklara çok yakındır. Bu da istatistikte “büyük sayılar kanunu” olarak bilinir.

TEKNOLOJİ DESTEKLİ OLASILIK ÖĞRETİMİ Son yıllarda olasılık konularını daha etkin öğretimi üzerine yapılan çalışmalarda öğrenmeyi kolaylaştırmak için öğrencilere mevcut fikirleri açıkça ortaya koyabilecekleri , birlikte tartışarak farklı düşünceleri değerlendirebilecekleri bir sosyal ortam oluşturulmaktadır. Bunların yanı sıra öğretimde kullanılan etkinliklerde öğrencilerin gerekli analizleri yapabilmelerini destekleyecek araçlar ve modellerde sağlanmaktadır. Ayrıca teknoloji kullanımını öğrencilerin tahminlerde yanılmalarına neden olan sezgisel kavramları test edip doğru olan kavramları geliştirmeleri açısından faydalı olduğu görülmüştür

Konold ve Kazak 4 çocuklu ailelerdeki erkek çocuk sayılarının dağılımı ile ilgili tahmin sorusu sorulmuştur. Eğer gerçek hayatta 4 çocuklu bir çok ailedeki erkek çocuk sayılarının sayısı grafiği çizilseydi, gerçek verilerde en çok benzeyen grafik aşağıdakilerden hangisi olurdu ?

10 9 8 7 6 5 4 3 2 1 0 Erkek çocuk sayısıErkek çocuk sayısı

İlk tahminlerde birçok öğrenci C grafiğini seçmiştir. Konold ve Kazak C grafiğindeki dağılımın tercih edilmesinde, öğrencilerin uçlardaki sonuçları pek mümkün bulmazken diğer olası sonuçları eşit olası görmüş olduklarına dayanarak hem eşit olasılık yanlığının hem de temsil kısa yolunun ortak bir rolü olabileceğini belirtmişlerdir. Bu tahmin sorusunda öğrencilerin önceden sahip oldukları sezgilere dayanan kavram yanılgılarının ortaya çıktığı görülmektedir. Bu da öğretmene ilk başta bu yanılgıları tespit etme fırsatı vermektedir. İlk tahminler yapıldıktan sonra ise öğrenciler her bir problemde durumla ilgili gerçek veriler toplayarak bunları analiz etmişlerdir.

Alternatif teorileri teşvik etmek amacıyla öğrencilere Abrahamson’ın çalışmasından esinlenmiş bir grup etkinliği yapmıştır bu etkinlikte ikili gruplar halinde çalışan öğrencilerin çubuk şeklinde kesilmiş dört bölmeli karton parçacıkları ile yeterinden fazla sayıda yeşil ve mavi daire şeklinde etiketler verilmiştir. Öğrencilerin görevi bu iki farklı renkte etiketleri her biri bir bölmeye gelecek şekilde dizip olabildiğince sayıda bu çubuklardan üretmektir.

Konold ve Kazak’ın in olasılık öğretimi için kullandıkları etkinliklerindeki yaklaşımın önemli bir özelliği öğrencilere daha önce sahip oldukları bilgiye ve sezgilere göre tahmin etme somut veri toplama ilk tahminlerini verilere dayanarak tekrar gözden geçirme, yeni bilgi ışığında başka olası bir teori geliştirme ve bunun geçerliliğini test etme fırsatları verilmesidir. Somut deneylerle ders saati içerisinde yeterli sayıda veri toplamak mümkün olmamaktadır. Bu nedenle Konold ve Kazak’ın geliştirdikleri etkinliklerin ileriki aşamalarında teknolojinin rolü oldukça büyüktür.

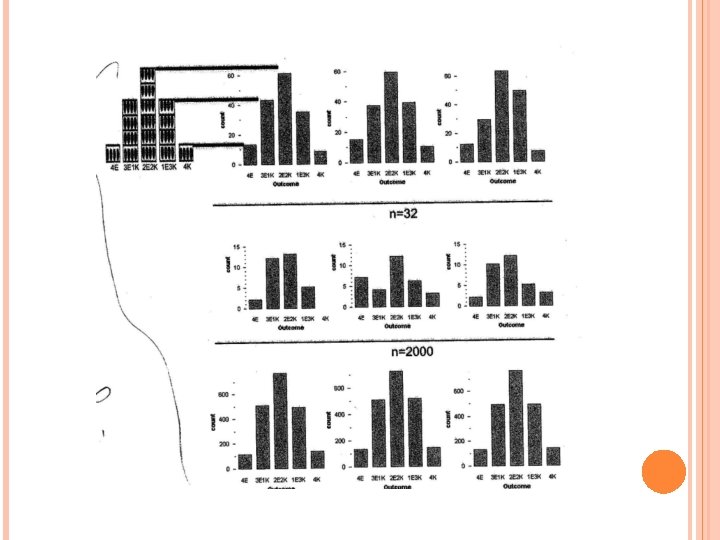
4 çocuklu ailelerin bilgisayar modeli. Üst sol köşedeki “ 4 Çocuklu Aileler” örnekleyici’sinde 4 kez üste karmaçtan çocukların cinsiyetini belirleyecek olan “K” ve “E” toplarında rastgele seçilerek toplamda 100 aile örneklenmiştir. Yukarıdaki tabloda çocukların cinsiyet sıralamaların(“E, K, E, E” “K, E, E, E” gibi) karmaçtan çıktıkça görülebilmektedir. Yukarıda sağdaki grafikte ise her bir çıktının yani 4 çocuklu ailelerdeki cinsiyet sıralamalarının sıklığı gösterilmektedir. Aşağıdaki grafikte ise çıktılar kız/erkek çocuk sayısına göre birleştirilerek gösterilmiştir.

Şekilde görüldüğü gibi öğrenciler soldaki model ile farklı örneklem büyüklüklerinde artarda yapılmış simülasyon sonuçlarını karşılaştırırken, her biri değişik 4 çocuklu aile tipini temsil eder çubukların göreli yüksekliklerine bakarak model ile uygunluğu kıyaslanmıştır. Bu analizlere göre , örneklem büyüklüğü 160 iken öğrenciler genelde modelle sonuçlar arasındaki uyumu “çok iyi” ya da “iyi” olarak değerlendirilmiştir. Örneklem büyüklüğü 32 olan ailelere bakmadan önce ise yalnızca birkaç öğrenci modelle sonuçlar arasında daha kötü bir uyum olacağını düşünürken sınıfça yapılan simülasyonlarda sonra diğer öğrencilerin şaşırmış oldukları görülmüştür nitekim örnekler büyüklüğü 32 ye düşürüldüğünde model ile çok alakası olmayan bambaşka sonuçlar elde edilebilmektedir öğrencilere örnekler büyüklüğü çok daha büyük olursa ne bekledikleri sorulduğundaysa pek çoğunun sonuçları modelle oldukça çok benzeyeceğini önceden tahmin edemedikleri görülmüştür.

Konold Kazak öğrencilerin sezgisel olarak geliştirdikleri bu olguyu şu şekilde açıklamışlardır: Büyük örneklemlerden alınan sonuçların beklenen (teori ) dağılıma oldukça yakın olmaları daha muhtemelken, küçük örneklemlerden sadece rastlantısal olarak beklenen dağılımdan oldukça farklı sonuçların çıkması daha olasıdır.

SONUÇ Olasılık konularının anlaşılmasının öğrenciler için oldukça zor olduğu yapılan araştırmalar sonucunda açıkça görülmektedir. Bir yanda öğrencilerin olasılıkla ilgili sezgileri ve kişisel deneyimleri sonucunda geliştirdikleri kavramların öbür yandan da olasılık kuramının sezgilere aykırı temel kavram ve prensiplerinin var oluşu öğrencilerin olasılık konularını öğrenmelerini zorlaştırmaktadır. Bu bölümde ele alınan gerek olasılık konularının öğrenciler tarafından anlaşılmasında karşılan zorluklar ve kavram yanılgıları gerekse yurt dışında bu konuların öğretiminde uygulanan kavramsal yaklaşımların, ülkemizdeki yeni matematik müfredatında ilköğretim 4. sınıftan itibaren başlayan olasılık öğretimi için sonuçları vardır.

Özellikle yeni matematik öğretim programında belirtildiği gibi erken yaşlardan başlayarak olasılık kavramının öğrencilerin sezgileriyle geliştirebileceği ortamların hazırlanmasında öğretmenlere, matematik eğitimci ve araştırmacılara büyük rol düşmektedir. Öğretmenler literatürde tespit edilen öğrencilerin sezgilerinden ve deneyimlerinden kaynaklanan yanılgılarının farkında olarak öğrencilerin olasılık kavramını geliştirmelerini sağlamalıdır.

HAZIRLAYAN LAR GÜLHAN ERDEMCİ YELİZ ŞENOCAK DİLEK BERRAK AYŞEGÜL AKBUDAK

BİZİ DİNLEDİĞİNİZ İÇİN TEŞEKKÜR EDERİZ.