Oil immersion objectives More light no total internal
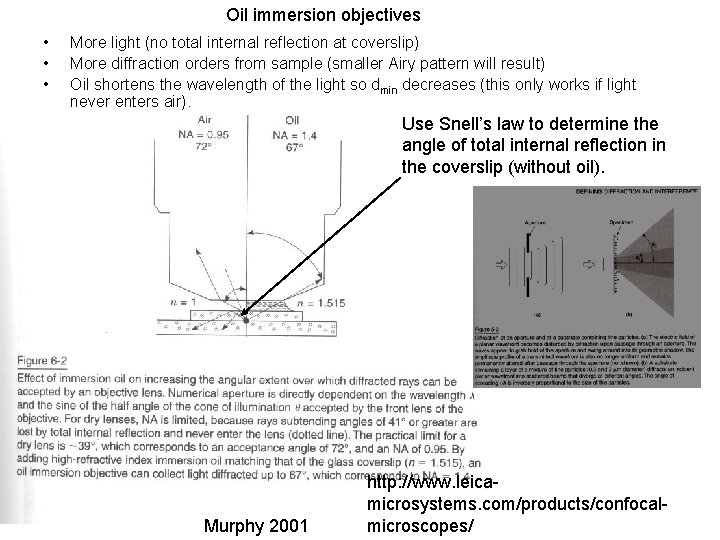
Oil immersion objectives • • • More light (no total internal reflection at coverslip) More diffraction orders from sample (smaller Airy pattern will result) Oil shortens the wavelength of the light so dmin decreases (this only works if light never enters air). Use Snell’s law to determine the angle of total internal reflection in the coverslip (without oil). Murphy 2001 http: //www. leicamicrosystems. com/products/confocalmicroscopes/


Adapted from Pawley 2004 dmin=1. 22 λ / 2 NA In terms of fundamentals of optics, for 2 points to be resolved, the max. of one object’s diffraction pattern must overlap the 1 st min. of the other. This is called the Raleigh/Abbe criterion. 500 um This 500 um scan range can be mapped to ? ? ? pixels. The scan itself can be other than 1: 1 aspect ratio but the pixels are each 1: 1. These represent light from the object as it is focused at the image plane. They are not points! ~1 micron (for a good oil objective) fast (? sec/scan) undersampled properly sampled In terms of instrumental sampling, we want 2 pixels to fit in the linear dimension of each pattern (4 pixels/area). Here we are matching our optical resolution to our instrumental resolution. This is called the Nyquist criterion. How can oversampling be a problem? Assuming the 1 micron dimension is correct, what is the size of each pixel? What do we mean by sampling? slow (4 sec/scan) Slowest (? sec/scan) When sampling with more pixels, adjust scan rate to increase photons/pixel; this is a good idea unless you are worried about beam damage! The top row of 3 scans (not in box) was done at constant scan rate (what is the scan rate for the top row? ) The photon flux from the sample in all cases is 16 photons/second. The Bio-Rad MRC 1024 (when not set to low signal) automatically corrects for changes in scan rate by decreasing PMT (photomultiplier tube) output at slower scan rates. With on, collect images at slow and normal scan rates (what are these rates in lines/sec)? How does this value relate to temporal (time) resolution? low signal turned

Axial or z resolution: zmin= 2 λair ηsample / (NAobj)2 z y y or x x University of Helsinki DON’T MEMORIZE When doing 3 D confocal microscopy, we want to match our corrected z-step with the proper sampling depth of our setup. It also helps some reconstruction programs if we can make our xy: z aspect ratio an interger value. This is ultimate z resolution, how does our z resolution change with confocal iris size? Adjust scan size, z step, scan rate, and pixel count to match your objective lens and sample. Now, image the sample with each of the above parameters set to nonoptimal settings.

During z-series acquisition the distance in z axis travel by the objective or sample is different than the change in z of the focal plane. The next 3 slides show why it is necessary to use a zcorrection factor when collecting stacks of optical sections (z-series).

When you turn the focus knob and move the objective 10 um closer to the sample what is the change in plane of focus in the sample? 20 X Extreme ray angle (degrees) 20 X 45 air, 28 glass, 32 water NA. 71 160 /. 17 160/. 17 microscope tube length coverslip thickness, 170 um α 1 Often, the WD printed on the objective actually is a measure of the distance between the objective front lens and the coverslip. 170 um given WD air α 1 190 um given (you can start at any focal distance you want to, just turn the focus knob) α 2 90 um 119 um WD water with coverslip

We use peripheral rays for correction factor. (Visser & N. S. White use modal rays, see ref. at end) Extreme ray angle (degrees) 20 X 45 air, 28 glass, 32 water NA. 71 160/. 17 10 um 170 um α 1 206 um (now we’ve moved the focus knob (objective) 10 microns closer to our sample) 90 um α 2 129 um

Gaussian z depth correction factor for z series reconstruction • NA = (refractive index of medium at lens) η x sin α • Nominal z-step = 10 um • Actual z-step = 16 um • Nominal z-step/correction factor = optical z-step • Correction factor =. 63 (also. 63 when simple equation used: η 1 x cosα 1 / η 2 x cosα 2 ) • Coversilp determines absolute focal depth but has no effect on focal shift with change in focal depth because its thickness is constant while the depth into sample is not. As described in Zill, 2000. Microscopy Research and Technique Volume 48 Issue 6, Pages 367 - 384. Based on work of Nick White and Stefan Hell from early 1990 s.

Be aware of spectral bleed through or leakage; picking up the same emissions in 2 or more channels. This can appear to be co-localization when it is not. Interestingly, these diagramatic grey filter bands shown here are much more like the leica SP 5 slits in shape than the older interference filters they are meant to represent in these spectra (interference filters do not have quite as sharp cut on/off characteristics). invitrogen. molecular. spectra. viewer
- Slides: 9