ODREENOST RAVNI AKSIOME O DVIJE RAVNI AKSIOME RASPOREDA










- Slides: 11

ODREĐENOST RAVNI AKSIOME O DVIJE RAVNI AKSIOME RASPOREDA

ODREĐENOST RAVNI Teorema 1: Postoji jedna i samo jedna ravan koja sadrži dvije prave koje se sijeku. ( Ravan je određena sa dvije prave koje se sijeku. ) Dokaz: Neka se prave a i b sijeku u tački C. Na osnovu druge aksiome ravni , na pravoj a postoji bar još jedna tačka A, a na pravoj b postoji bar još jedna tačka. B. Tačke A, B, C su nekolinearne tačke ( u suprotnom prave a i b bi se poklapale) pa na osnovu prve aksiome ravni one određuju tačno jednu ravan α. Pošto tačke A, C pripadaju pravoj a i takođe ravni α, to znači da prava a pripada ravni α ( aksioma o pravoj i ravni). Na isti način zaključujemo da i prava b pripada ravni α. Prema tome ravan α sadrži prave a i b. Dokažimo još da je ravan α jedina ravan koja sadrži prave a i b. Pretpostavimo suprotno: tj da postoji ravan β koja sadrži prave a i b. Pošto je a⊂ β to i A, C∊ β jer je A, C ∊a. Analogno pošto b ⊂ β to su i B, C ∊ β jer su B, C ∊ b, a to znači da ravan β sadrži tačke A, B, C, koje sadrži i ravan α, pa je α= β.

Teorema 2: Postoji jedna i samo jedna ravan koja sadrži datu pravu i datu tačku koja ne pripada toj pravoj. ( Ravan je određena sa pravom i tačkom van te prave. ) Dokaz: Neka su date prava a i tačka C koja ne pripada pravoj a. Na pravoj a izaberimo tačke Ai. B. Sada su tačke A, B, C tri nekolinearne tačke i one određuju tačno njednu ravan α (prema prvom aksiomu ravni). Pošto A, B ∊a, i A; B∊ α to na osnovu aksiome prave i ravni a⊂ α. Prema tome ravan α je ravan koja sadrži pravu a i tačku C. Ako bi postojala neka druga ravan β koja sadrži pravu a i tačku C , ona bi sadržavala i nekolinearne tačke A , B, C pa bi se poklapala sa ravni α. (prva aksioma ravni)

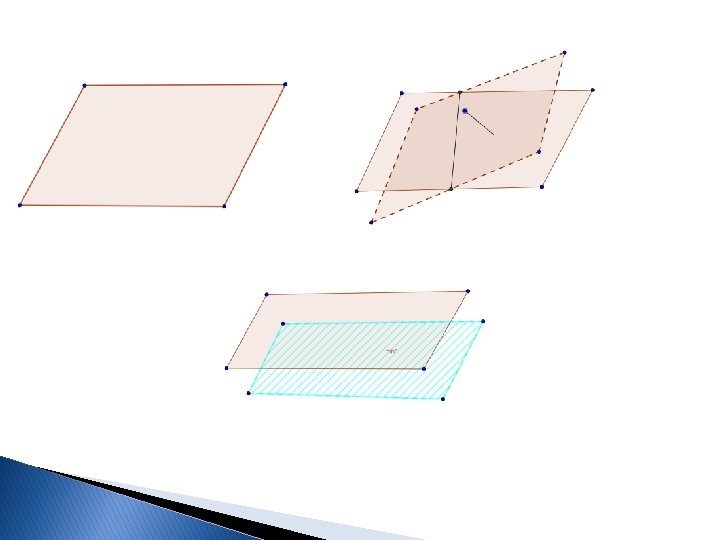
AKSIOMA O DVIJE RAVNI A 8: Ako dvije ravni imaju jednu zajedničku tačku onda one imaju još jednu zajedničku tačku. Odavde zaključujemo da ako dvije ravni imaju jednu zajedničku tačku onda one imaju zajedničku pravu. Iz ove aksiome slijedi da su moguća svega tri uzajamna položaja dvije ravni. a) Ako ravni α i β imaju tri zajedničke nekolinearne tačke tada je α = β b) Ako α i β imaju zajedničku tada je α ∩ β = p i kažemo da se ravni α i β sijeku po pravoj p c) Ako ravni α i β nemaju zajedničkih tačaka tj ako je α ∩ β =∅ , tada su α i β paralelne što označavamo sa α ∥ β.


Zadatak 1 : Koliko je najviše ravni određeno sa četiri različite tačke? Rješenje: Najviše ravni će biti određeno ako su sve četiri tačke nekomplanarne. Ako su A, B, C, D nekomplanarne tačke one određuju sljedeći ravni: ABC, ABD, ACD, BCD – dakle imamo četiri ravni. Zadatak 2: Koliko je najviše ravni određeno sa pravom p i tri nekolinearne tačke? Rješenje: Najviše ravni će biti u slučaju da prava p ne pripada ravni koja je određena sa tačkama A, B, C, kao i da ni jedna od tih tačaka ne pripada pravoj p. Tada imamo sljedeće ravni: ABC, p. A, p. B, p. C – dakle ukupno imamo četiri ravni.

Zadatak 3: Koliko je ravni određeno sa n različitih tačaka? Rješenje: Najviše ravni će biti određeno u slučaju da su svake četiri tačke nekomplanarne. Njihov broj je tada dat formulom: Zadatak 4: Koliki je najmanji broj tačaka kojima je određeno 20 ravni? Rješenje: Na osnovu prethodnog primjera imamo:

AKSIOMA PARALELNOSTI DVIJE RAVNI Def: Za dvije prave p q koje leže u istoj ravni kažemo da su paralelne i zapisujemo p ∥ q ako je p=q ili p ∩ q = ∅. A 9: Ako tačka A i prava p pripadaju istoj ravni α , onda tačkom A prolazi tačno jedna prava koj pripada ravni α iparalelna je sa pravom p. Teorema: Postoji tačno jedna ravan koja sadrži dvije date paralelne prave. ( Ravan je određena sa dvije različite paralelne prave ) Dokaz: Neka su p i q date paralelne prave. Na osnovu definicije paralelnosti p i q leže u jednoj ravni α. Dokažimo da ne postoji druga ravan βkoja sadrži prave p i q. Na pravoj p uzmimo tačke A i B a na pravoj q tačku C. Ako bi ravan β sadržavala prave p i q onda bi ona sadržavala i nekolinearne tačke A, B, C pa bi se poklapala sa ravni α.

Tore ma : Ako prave p q i r leže u jednoj ravni α i ako su prave p i q paralelne i ako prava r siječe pravu p tada ona siječe i pravu q. Dokaz: Neka r sijeće pravu p u tački P. Pretpostavimo da r ne siječe pravu q. Tada kroz tačku P prolaze dvije prave koje su paralelne pravoj q (p i r), što jenemoguće prema A 9. Došli smo do kontradikcije do koje nas je dovela pretpostavka da prava r ne siječe pravu q, što znači da prava r mora sječi pravu q.

AKSIOME RASPOREDA A 1: Ako je tačka B između tačaka A i C to jest A-B-C onda su A, B, C tri kolinearne tačke i tada je B između tačaka C i A tj. C-B-A. A 2: Za svake dvije tačke Ai. B postoji tačka C tako da je A-B-C. A 3: Ako su A, B, C tri kolinearne tačke , može postojati najvišejedan od ova tri odnosa: A-B-C; A-C-B ; B-A-C ; PEANOV aksiom: Neka su A, B, C tri nekolinearne tačke, i p prava takva da ni jedna od datih tačaka ne pripada pravoj p. Ako postoji tačka D ∊ p ivrijedi A-D-B, onda postoji i tačka E∊p i zakoju vrijedi A-E-C ili B-E-C. Pašov aksiom iskazuje jednostavnu činjenicu, da prava koja ne sadrži ni jednu od nekolinearnih tačaka A, B, C i siječe jednu stranicu trougla ABC, mora siječi još jednu stranicu tog trougla.

Teorema: Za svake dvije tačke A, B postoji tačka C koja je između tačaka A i B. Dokaz: Postoji tačka D takva da su A, B, D nekolinearne tačke. Postoji E∊AD takva da je A-D-E Postoji F∊EB takva da je E-B-F Prava DF ne sadrži ni jednu od tačaka A, B, E ali sadrži tačku. D za koju je A-D-E, zato na osnovu Pašove aksiome Postoji tačka C∊DF takva da je A-C-B ili postoji C∊ DF Takva da je E-C-B. U drugom slučaju bi bilo DF∩EB=(C, F) pa bi DF i EB bile ista prava. To nije ispunjeno jer D∊DF i D∉ EB, a to znači da mora biti C∊DF i A-C-B. Završni dio: Ponavljanje i provjera usvojenosti gradiva. ZADAČA: Više puta isčitati aksiome razmišljajući o njihovim tvrdnjama, kako bi se bolje razumijela njihova primjena.