ODJEL ZA FIZIKU Sveuilita Josipa Jurja Strossmayera u

ODJEL ZA FIZIKU Sveučilišta Josipa Jurja Strossmayera u Osijeku Osnove fizike 3 Prema knjizi: Planinić, J. , Osnove fizike III (Valovi – akustika – optika uvod u atomsku fiziku), Filozofski fakultet Osijek, 2004. 2020. /2021. http: //www. fizika. unios. hr/of 3/ http: //gama. fizika. unios. hr/~branko/of 3. htm

OSNOVE FIZIKE 3 nastavnik: izv. prof. dr. sc. Branko Vuković asistentica: Jelena Strišković, prof učionica: 60 konzultacije: ponedjeljak, 10 -11 sati (soba 39) e-mail: branko@fizika. unios. hr

Autor većine animacija i primjera srednjoškolskih zadataka u ovoj prezentaciji je Jakov Labor, profesor fizike u Gimnaziji Antuna Vrančića u Šibeniku. Profesor je autor nekoliko udžbenika iz područja fizike, a na njegovom youtube kanalu mogu se naći brojni video zapisi pokusa iz raznih područja fizike. Linkovi: https: //www. youtube. com/results? search_query=jakov+labor https: //www. youtube. com/channel/UC 2 i 39 ILw. B 92 Bw. YEZUeat. Ltw/videos Zahvaljujem se profesoru Jakovu Laboru.

ISPITI: Ø Kolokviji, seminar, zadaće, završni ispit

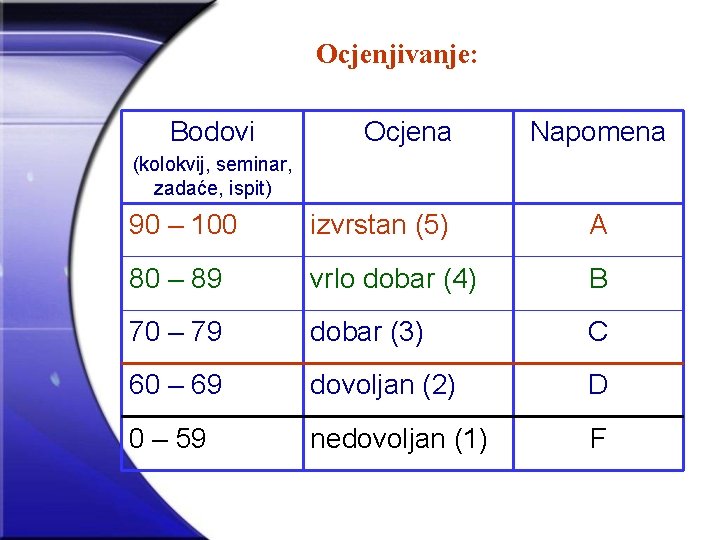
Ocjenjivanje: Bodovi Ocjena Napomena (kolokvij, seminar, zadaće, ispit) 90 – 100 izvrstan (5) A 80 – 89 vrlo dobar (4) B 70 – 79 dobar (3) C 60 – 69 dovoljan (2) D 0 – 59 nedovoljan (1) F

OSNOVE FIZIKE III - literatura Planinić, J. , Osnove fizike III (Valovi – akustika – optika - uvod u atomsku fiziku), Filozofski fakultet Osijek, 2004. Cindro, N. , Fizika 1, Školska knjiga, Zagreb, 1988. Gibbs, K. , Advanced Physics, Cambridge University Press, Cambridge, 1988. Henč-Bartolić, V. , Kulišić, P. , Valovi i optika, Školska knjiga, Zagreb, 1991. Krane, K. , Modern Physics, J. Wiley and Sons, New York, 1996. Paić, M. , Gibanje, Sile, Valovi, Liber, Zagreb, 1997. Paić, M. , Osnove fizike, IV dio, Sveučilišna naklada Liber, Zagreb, 1983. Young, H. , Freedman, R. , University Physics, Addison-Wesley Publ. , New York, 2020.

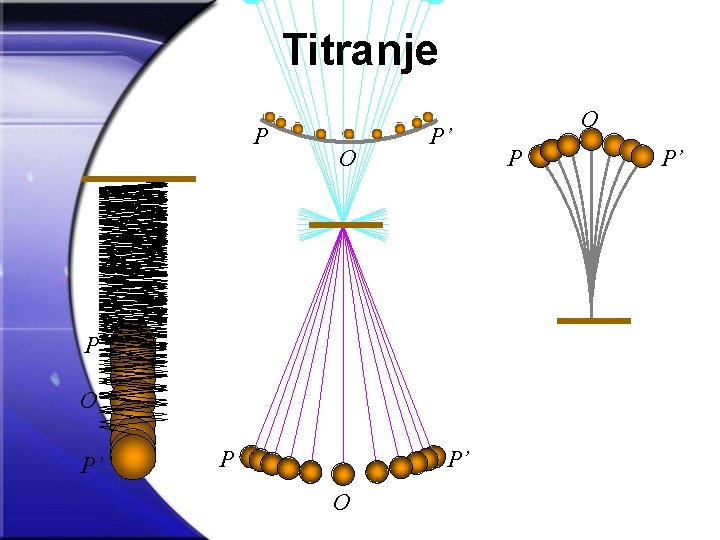
Titranje P O P’ P P’ O O P P’

TITRANJE - ponavljanje Titranje – periodično gibanje tijela po putanji koja se ponavlja. Primjeri: Ø jednoliko gibanje po kružnici Ø gibanje njihala oko ravnotežnog položaja Ø vibracije žice Ø atomi u rešetkama čvrstih tijela Ø električno i magnetsko polje

TITRANJE: pokusi Kolekcija pokusa profesora Jakova Labora: http: //www. prirodopolis. hr/labor/ Pokus broj 1 - 4:

TITRANJE 2 pomak, izduženje ili elongacija (x) - udaljenost tijela od ravnotežnog položaja Amplituda (A) - maksimalna elongacija Period (T) - vrijeme potrebno za jednu oscilaciju frekvencija (n) - ukupan broj oscilacija u sekundi Harmoničko titranje – ono titranje koje se odvija po zakonu sinusa Harmoničko titranje se dobije kada je sila koja izvodi titranje razmjerna udaljenosti tijela od ravnotežnog položaja (elongaciji).

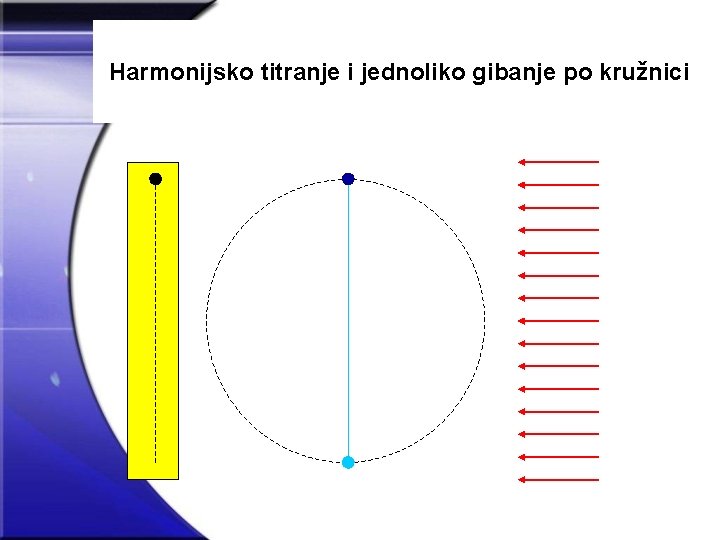
Harmonijsko titranje i jednoliko gibanje po kružnici

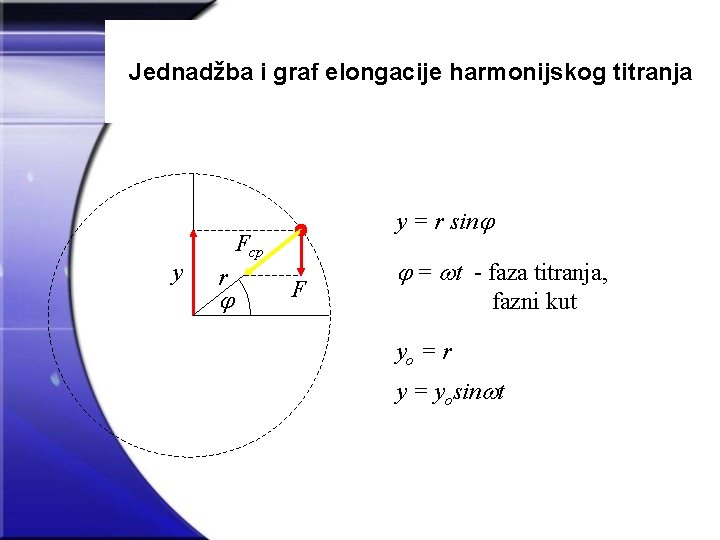
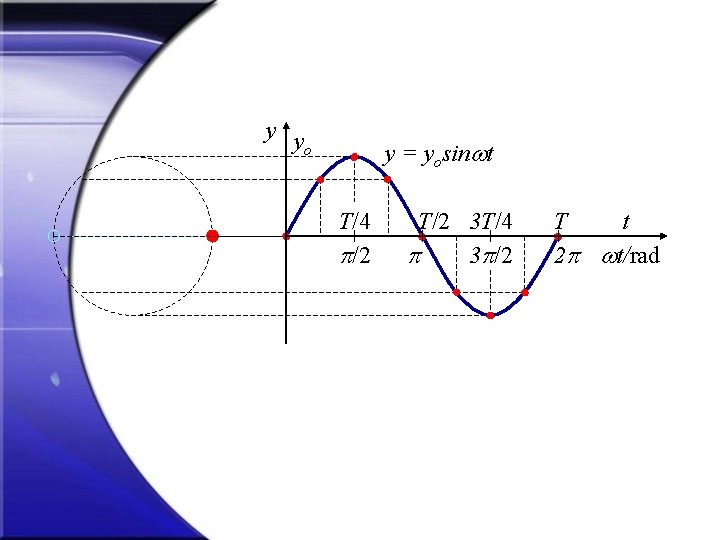
Jednadžba i graf elongacije harmonijskog titranja y y = r sin Fcp r F = t - faza titranja, fazni kut yo = r y = yosin t

Kolekcija pokusa profesora Jakova Labora: http: //www. prirodopolis. hr/labor/ Pokusi broj 5 i 7

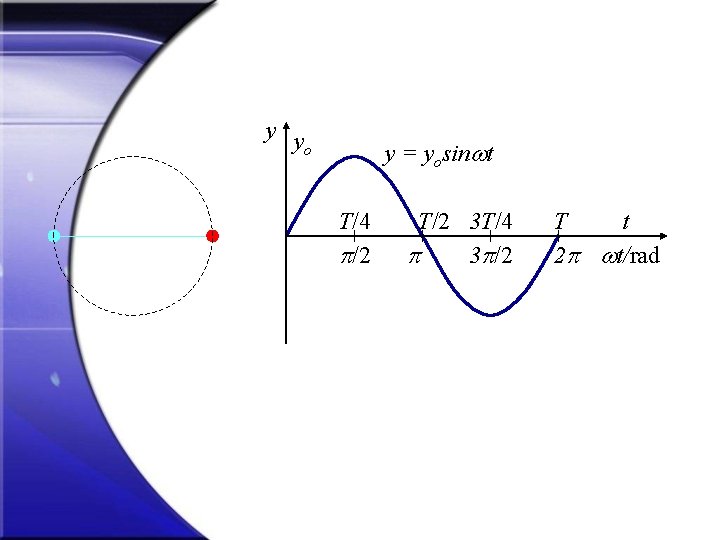
y y o y = yosin t T/4 /2 T/2 3 T/4 3 /2 t T 2 t/rad

y y o y = yosin t T/4 /2 T/2 3 T/4 3 /2 t T 2 t/rad

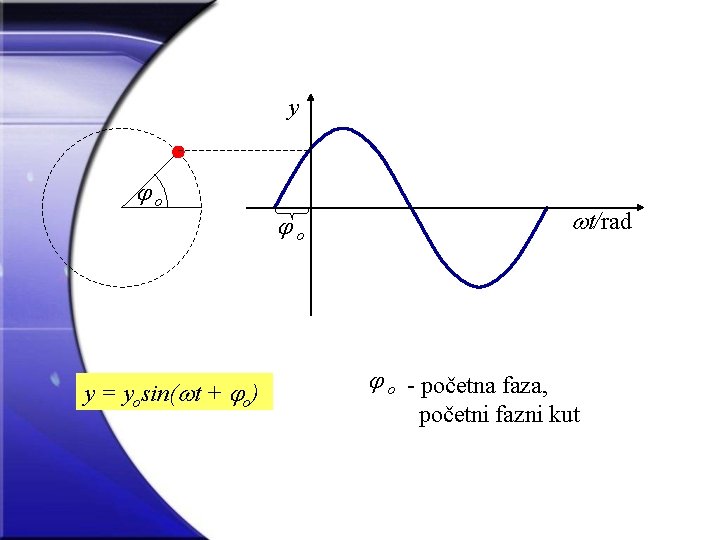
y o y = yosin( t + o) t/rad o o - početna faza, početni fazni kut

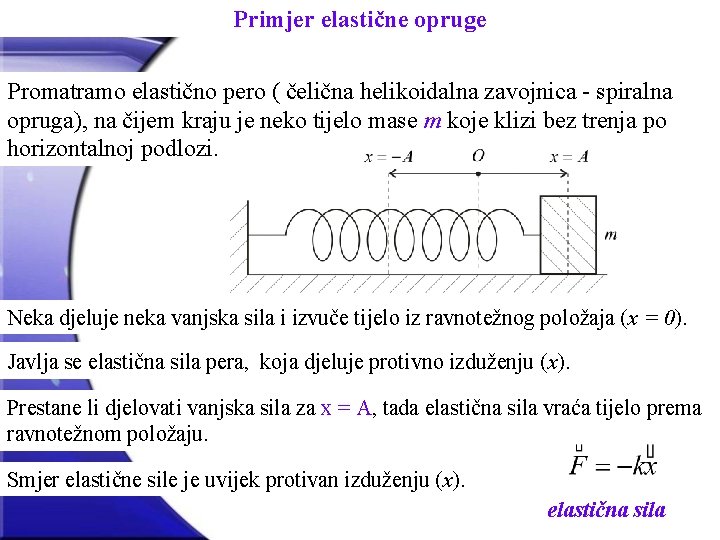
Primjer elastične opruge Promatramo elastično pero ( čelična helikoidalna zavojnica - spiralna opruga), na čijem kraju je neko tijelo mase m koje klizi bez trenja po horizontalnoj podlozi. Neka djeluje neka vanjska sila i izvuče tijelo iz ravnotežnog položaja (x = 0). Javlja se elastična sila pera, koja djeluje protivno izduženju (x). Prestane li djelovati vanjska sila za x = A, tada elastična sila vraća tijelo prema ravnotežnom položaju. Smjer elastične sile je uvijek protivan izduženju (x). elastična sila

SVAKA ELASTIČNA SILA UZROKUJE HARMONIJSKO TITRANJE! diferencijalna jednadžba drugog reda Rješenje? Koja funkcija nakon druge derivacije postaje ona sama? eksponencijalna, sinus, cosinus

Pretpostavimo rješenje i uvrstimo ga u jednadžbu: (*) Period = ? Iz uvjeta kružna frekvencija titranja Harmonijski oscilator – svako tijelo koje vremenski titra prema jednadžbi (*)

fazni pomak ili pomak u fazi Iz početnih uvjeta, npr. t = 0, uteg u ravnoteži

Pokus: Zamislimo mnoštvo harmoničkih oscilatora poredanih jedan kraj drugog. Pobudimo prvi oscilator. Što se događa? Širenje poremećaja u prostoru! Val – širenje poremećaja u prostoru Valovi – jedna od najraširenijih pojava u prirodi Širenje poremećaja u prostoru može biti pravilno ili nepravilno.

VALOVI Elastična tijela - Imaju svojstvo ponovnog zauzimanja početnog oblika nakon što je na njih djelovala sila (kratkotrajno) i deformirala ih (izobličila, promijenila mu oblik). Elastičnost u prirodi? Imaju ga skoro sva tijela (više ili manje). Savršeno kruto tijelo (kada bi postojalo) Nema sposobnost deformacije, nego bi se pod djelovanjem sile jedino moglo gibati kao jedinka, jedno tijelo. Nema svojstva prijenosa djelovanja mehaničke sile među česticama. Elastično tijelo (ili sredstvo) - Postoje elastične veze između čestica, pa pomak čestica u jednom dijelu tijela, tj. elastična deformacija, uzrokuje pomak susjednih čestica. Zbog inercije čestica deformacije se ne prenose trenutačno, nego s nekom konačnom brzinom koja zavisi o elastičnim svojstvima te tvari.

VALOVI 2 Djelovanje vanjskih sila u nekom elastičnom sredstvu prenosi se postupno na ostale dijelove sredstva, ili sustava, tzv. valno gibanje. Postupan prijenos poremećaja u sredstvu prenosi se u obliku vala, pa kažemo da se tada u sredstvu širi val. Primjer: Ispustimo kamen u vodu poremećaj ili val. Kolekcija pokusa profesora Jakova Labora: http: //www. prirodopolis. hr/labor

VALOVI 2 Djelovanje vanjskih sila u nekom elastičnom sredstvu prenosi se postupno na ostale dijelove sredstva, ili sustava, tzv. valno gibanje. Postupan prijenos poremećaja u sredstvu prenosi se u obliku vala, pa kažemo da se tada u sredstvu širi val. Primjer: Ispustimo kamen u vodu poremećaj ili val. Općenito: Valno gibanje je prijenos energije i količine gibanja iz jedne točke prostora u drugu, bez prijenosa tvari.

VALOVI 3 Promatramo elastično sredstvo u ravnoteži: Na mali dio sredstva djeluje u kratkom vremenu promjenjiva sila. Na mjestu djelovanja tada sila izvodi vremenski promjenljivu elastičnu deformaciju sredstva koju nazivamo valni puls ili poremećaj. (http: //www. prirodopolis. hr/labor) Deformirani dio sredstva U dodiru sa susjednim dijelovima. Djelovanje na njih. Poremećaj ili puls se pomiče kroz sredstvo, tj. puls se širi sredstvom kao val.

VALOVI 4 Pretpostavimo da je djelovanje sile u vremenu proizvelo u elastičnom sredstvu takav poremećaj da su sve čestice ili materijalne točke ravnine P 1 pomaknute u danom trenutku za jednake vektore pomaka: , Sve materijalne točke ravnine P 1 nalaze se u novoj ravnini P 1' Nakon nekog vremena. Lokalna deformacija prouzročit će sličnu deformaciju u nekoj susjednoj ravnini P 2 , koja će biti pomaknuta u novi položaj P 2'. Tako se nastali valni puls, u obliku elastičnog vala pomaka, širi kroz sredstvo brzinom. Općenito: Pomaci dviju ravnina, P 1 i P 2, ili više ravnina, ne moraju biti međusobno jednaki.

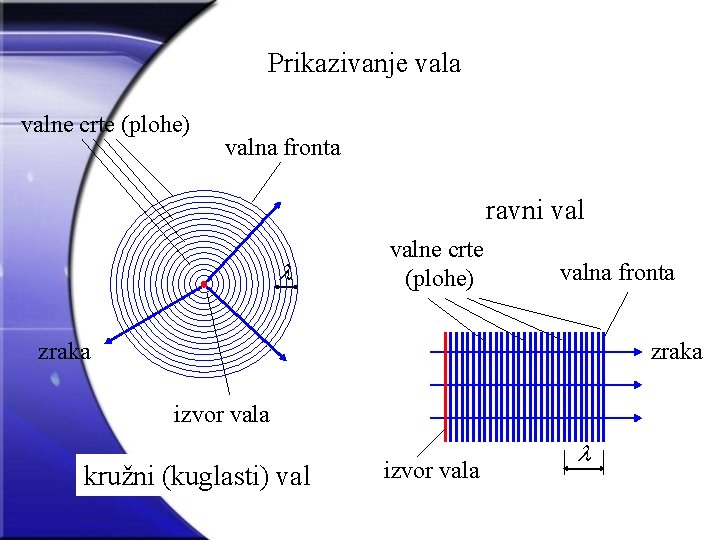
VALOVI 5 Općenito: Pomaci dviju ravnina, P 1 i P 2, ili više ravnina, ne moraju biti međusobno jednaki. Ravnina u kojoj materijalne točke imaju jednake vektore pomaka naziva se valna ravnina. Međusobno paralelne valne ravnine imaju materijalne točke u jednakom stanju gibanja, odnosno te točke imaju jednake vektore pomaka. Val s paralelnim valnim ravninama nazivamo ravnim valom. Pravac okomit na valnu ravninu je pravac nositelj brzine širenja vala, a nazivamo ga i valnom zrakom. Odnos vektora pomaka u odnosu na valnu ravninu određuje vrstu vala:

Prikazivanje vala valne crte (plohe) valna fronta ravni valne crte (plohe) valna fronta zraka izvor vala kružni (kuglasti) val izvor vala

VALOVI 6 Odnos vektora pomaka u odnosu na valnu ravninu određuje vrstu vala: longitudinalni (uzdužni) val - Vektor pomaka čestica sredstva je okomit na valnu ravninu, odnosno paralelan s valnom zrakom. longitudinalni val čestice se gibaju ili titraju uzduž pravca širenja vala. x – pravac širenja vala Ai Ai' – Titranje točke

VALOVI 7 Odnos vektora pomaka u odnosu na valnu ravninu određuje vrstu vala: transverzalni (poprječni) val - Vektori pomaka materijalnih točaka leže u valnim ravninama, odnosno okomiti su na valnu zraku. transverzalni val čestice sredstva titraju okomito na smjer širenja vala x – pravac širenja vala Ai Ai' – Titranje točke

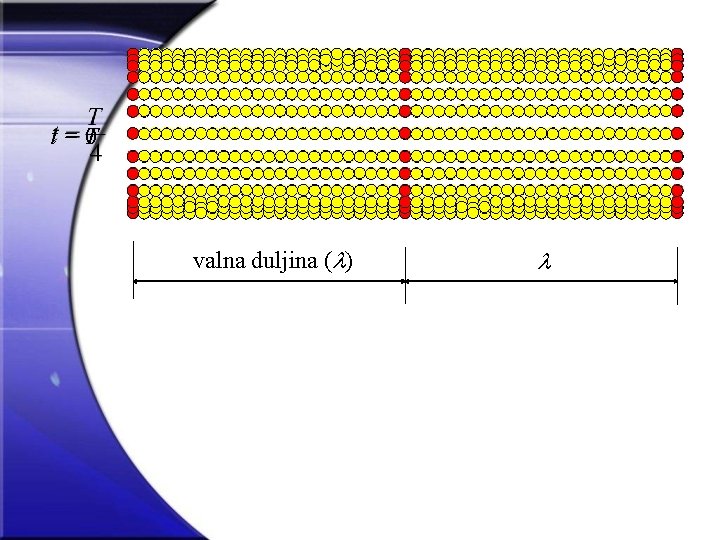
t=T 0 valna duljina ( )

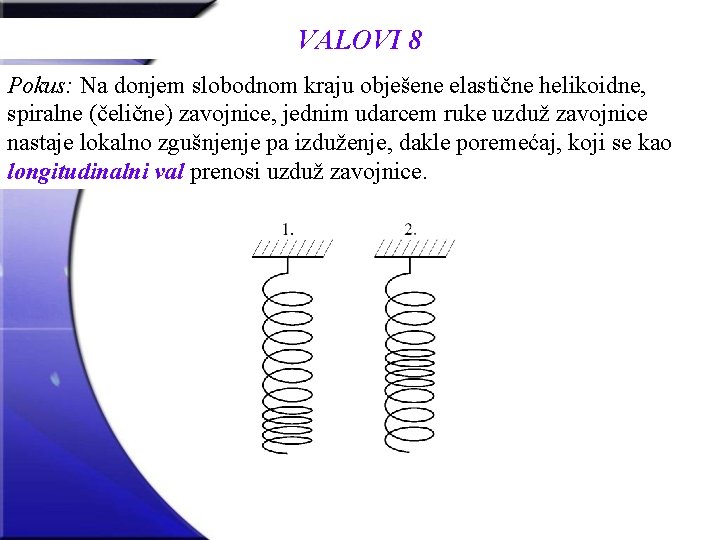
VALOVI 8 Pokus: Na donjem slobodnom kraju obješene elastične helikoidne, spiralne (čelične) zavojnice, jednim udarcem ruke uzduž zavojnice nastaje lokalno zgušnjenje pa izduženje, dakle poremećaj, koji se kao longitudinalni val prenosi uzduž zavojnice.

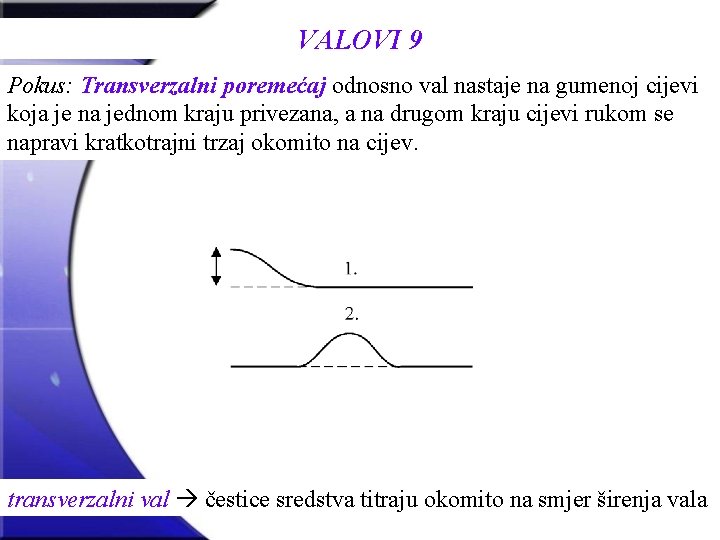
VALOVI 9 Pokus: Transverzalni poremećaj odnosno val nastaje na gumenoj cijevi koja je na jednom kraju privezana, a na drugom kraju cijevi rukom se napravi kratkotrajni trzaj okomito na cijev. transverzalni val čestice sredstva titraju okomito na smjer širenja vala

VALOVI 10 Elastično sredstvo čvrstog stanja - longitudinalni i transverzalni valovi Fluidi - samo longitudinalni valovi Objašnjenje: Za pojavu transverzalnog vala potrebne su sile koje se protive pomicanju jednog sloja sredstva prema susjednom sloju(u fluidima su takve sile zanemarive). Transverzalni valovi su mogući samo u tijelima čvrstog stanja, a longitudinalni valovi se mogu širiti u sredstvima svih agregatnih stanja (čvrstog, tekućeg i plinovitog). Primjeri longitudinalnih valova: a) Vlak na kojemu se priključuje lokomotiva (pomak od udarca lokomotive prenosi se na vlaku od vagona do vagona). b) U dugoj cijevi ispunjenoj fluidom (plinom ili tekućinom), kada se na jednom kraju u cijevi klip (stap) giba periodično naprijed-natrag. Val se sastoji od periodično izmjeničnih područja kompresije (zgušnjenja) i dilatacije (razrjeđenja) plina.

Zadatak: Transverzalni harmonijski val širi se uzduž horizontalnog pravca brzinom 5 m s-1. Dvije najbliže čestice sredstva, od kojih je jedna u pozitivnom, a druga istodobno u negativnom amplitudnom položaju, međusobno su horizontalno udaljene 25 cm. Kolika je: a) valna duljina i b) frekvencija vala? Rješenje: v = 5 m s-1 d = 25 cm b) a) d , = 2 d = 2· 25 cm = 50 cm = 0, 50 m f = 10 Hz

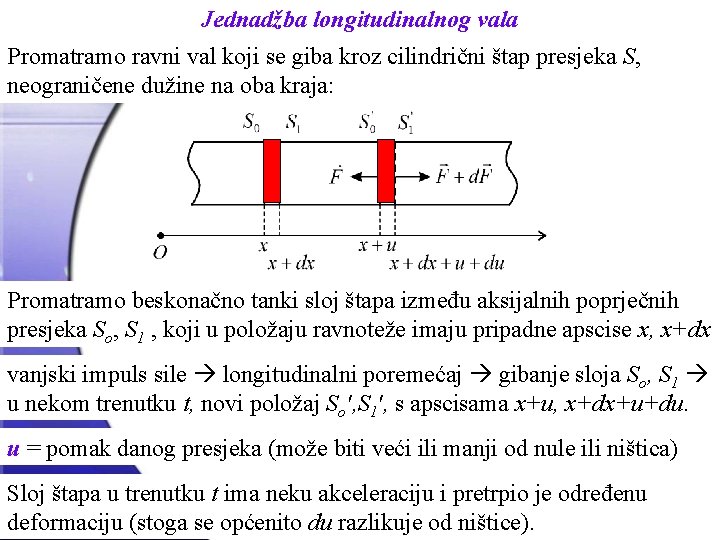
Jednadžba longitudinalnog vala Promatramo ravni val koji se giba kroz cilindrični štap presjeka S, neograničene dužine na oba kraja: Promatramo beskonačno tanki sloj štapa između aksijalnih poprječnih presjeka So, S 1 , koji u položaju ravnoteže imaju pripadne apscise x, x+dx vanjski impuls sile longitudinalni poremećaj gibanje sloja So, S 1 u nekom trenutku t, novi položaj So', S 1', s apscisama x+u, x+dx+u+du. u = pomak danog presjeka (može biti veći ili manji od nule ili ništica) Sloj štapa u trenutku t ima neku akceleraciju i pretrpio je određenu deformaciju (stoga se općenito du razlikuje od ništice).

Jednadžba longitudinalnog vala 2 Kad se val počeo širiti, tj. kad su poremećaji već nastupili, unutar sredstva počinje djelovati elastična sila (zbog elastičnog naprezanja čvrstog tijela). Na presjek So' djeluje sila F, a na S 1' sila F+d. F (protivnog smjera, u smislu udaljavanja od ravnotežnog položaja). Neuravnotežena sila d. F daje ubrzanje sloju So', S 1'. Kako naći jednadžbu gibanja sloja?

Jednadžba longitudinalnog vala 3 Kako naći jednadžbu gibanja sloja? Koristimo zakone mehanike (Newtonove zakone). Kolika je masa sloja debljine dx? r = gustoća nenapregnutog sloja sredstva (gustoća štapa) S = površina presjeka štapa 2. Newtonov zakon (sila daje ubrzanje a) Pomak u je funkcija položaja i vremena, u = u(x, t)

Jednadžba longitudinalnog vala 4 Što dalje? Koristimo Hookeov zakon koji daje vezu između specifičnog izduženja sloja, du/dx, presjeka S i modula elastičnosti E (što je tzv. Youngov modul elastičnosti): Dl/l = relativno izduženje U našem slučaju Parcijalna diferencijalna jednadžba drugog reda koja opisuje longitudinalno valno gibanje u elastičnom sredstvu.

Jednadžba longitudinalnog vala 5 Što predstavlja E/r? Dimenzija je: Koja fizikalna veličina ima dimenziju ms-1? Rješenje? Pretpostavljamo rješenje dif. jednadžbe u obliku funkcije u(x, t): f(x, t) i (x, t) su neke derivabilne funkcije (dakle imaju derivacije 1. i 2. reda po x i t).

Jednadžba longitudinalnog vala 6 Provjera: Lijeva i desna strana jednadžbe su identične. u je rješenje valne jed. Funkcija u(x, t) = zbroj dviju funkcija: f(vt-x) funkcija valnog gibanja u pozitivnom smjeru osi x, j(vt+x) funkcija valnog gibanja u protivnom smjeru (protivan predznak od x), odnosno u negativnom smjeru osi x.

Jednadžba longitudinalnog vala 7 Općenito: Funkcija u(x, t) sastavljena je od dva gibanja uzduž osi x u suprotnim smjerovima. Pribrajanje dviju valnih funkcija, koje daju jednu rezultantnu funkciju vala, nazivamo principom superpozicije (prema kojem svaki val proizvodi svoje titranje neovisno o postojanju drugog vala). Širenje jednoga ravnog vala ili poremećaja može se opisati samo jednom od funkcija u zbroju, npr: u 1= u 1(x, t), tj. u 1 zavisi o položaju i vremenu funkcija u se može promatrati u ovisnosti o jednoj varijabli (i onda dvodimenzionalno prikazati), dok se za drugu varijablu uzima da ima konstantnu vrijednost

Jednadžba longitudinalnog vala 8 u 1= u 1(x, t), tj. u 1 zavisi o položaju i vremenu funkcija u se može promatrati u ovisnosti o jednoj varijabli (i onda dvodimenzionalno prikazati), dok se za drugu varijablu uzima da ima konstantnu vrijednost Primjer: Ravninu presjeka kojeg promatramo stavimo u ishodište, onda je x = 0 , pa funkcija u 1 postaje: Primjer kratkotrajnog pulsa: Slično se može promatrati funkcija u ovisnosti samo o x , npr. u trenutku t = 0.

Jednadžba longitudinalnog vala 9 Funkcija f u gornjem izrazu mora biti definirana za svaki argument pa i za vrijednost 0 v = brzina poremećaja koji se širi u pozitivnom smjeru osi x Brzina v ne zavisi o obliku poremećaja (ne zavisi o funkciji f (vt – x)). Brzina širenja vala v se još zove fazna brzina vala: Brzina kojom se pomiču čestice elastičnog sredstva:

Brzina širenja longitudinalnog vala - korisne formule u čvrstim tijelima E [N m-2]- Youngov modul elastičnosti - gustoća u plinovima - adijabatska konstanta R – opća plinska konstanta T – apsolutna (termodinamička) temperatura M – molarna masa

Brzina vala u plinovima pri temperaturi 0 o. C? brzina pri temperaturi 0 o. C Za zrak: = 1, 40, M = 0, 029 kg mol-1

Zadatak: Na jednom kraju bakrene cijevi duljine 366 m čekićem se proizvede zvučni signal. Do drugog kraja cijevi zvuk stigne 1 s prije nego kroz zrak. Koliki je Youngov modul elastičnosti bakra, ako je brzina zvuka u zraku 330 m s-1? Gustoća bakra je 8900 kg m-3. Rješenje: l = 366 m t = 1 s vz = 330 m s-1 = 8900 kg m-3 E=? , tz = 1, 11 s tb = tz - t = 1, 11 s – 1 s , tb = 0, 11 s , vb = 3327 m s-1 , E = 9, 85· 1010 N m-2

Sinusni ravni val Funkcija u (rješenje diferencijalne jednadžbe valnog gibanja) može imati jednostavan oblik periodične sinusne funkcije (slučaj kada poremećaj u elastičnom sredstvu izvodi harmonički oscilator, koji titra po sinusnom zakonu) širenje takvih pomaka naziva se i harmoničkim valom, npr. za točku u ishodištu: Čestice koje se nalaze na udaljenosti x od ishodišta počet će titrati kasnije (dok se poremećaj pomakne na putu x) sa zakašnjenjem Dt = x/v (gdje je v brzina pomaka poremećaja). Kažemo da je čestica na položaju x pomaknuta u fazi s obzirom na titranje čestice u ishodištu. Čestica na položaju x će titrati prema sljedećoj jednadžbi:

Sinusni ravni val 2 Uvodeći vezu perioda titranja i kružne frekvencije: Oblik funkcije koji smo susreli ranije, f(vt-x), a opisuje širenje vala u smjeru osi + x. Kako se pojavljuje u fazi sinusne funkcije, veličinu v nazivamo faznom brzinom. Slično, u negativnom smjeru osi x, širi se val opisan sljedećom funkcijom:

Sinusni ravni val 3 T = Vremenski period sinusne funkcije u kojem čestica izvede cijeli (puni) titraj. Kako se val (poremećaj) giba stalnom brzinom v, onda će na udaljenosti v. T = l čestica biti u istom stanju titranja. Na jednakim razmacima l ponavljaju se jednake, iste faze gibanja i onda je l prostorni period funkcije f(vt-x), ili funkcije u(x, t), a naziva se valna duljina. Valna duljina je udaljenost između dviju najbližih čestica vala koje su u istom stanju titranja, tj. između kojih je razlika faza 2 p. Kažemo da je l prostorni, a T vremenski period vala.

Sinusni ravni val 4 Slično, u negativnom smjeru osi x širi se val: Promatrajmo ravni val za položaje x = 0 i x = l: Kažemo da val na mjestu x = l zaostaje u fazi za j = 2 pl/ (s obzirom na val u ishodištu).

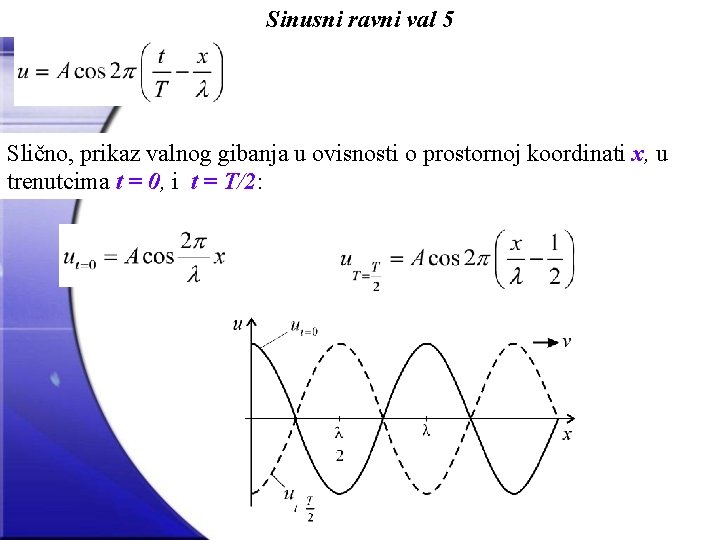
Sinusni ravni val 5 Slično, prikaz valnog gibanja u ovisnosti o prostornoj koordinati x, u trenutcima t = 0, i t = T/2:

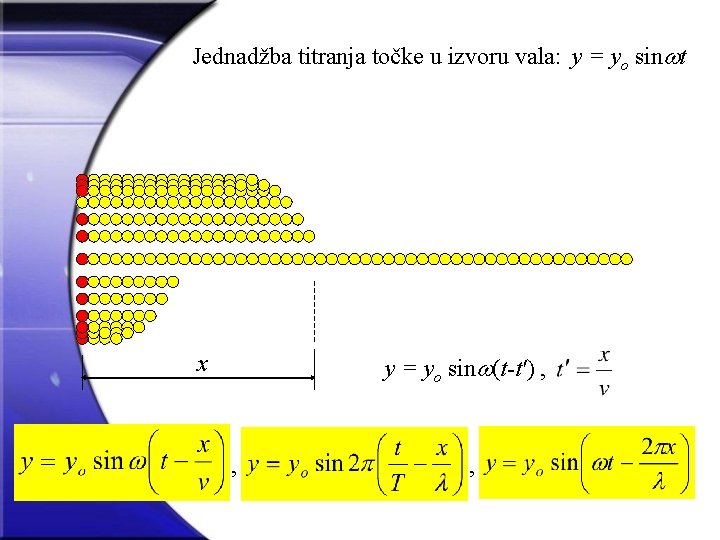
Jednadžba titranja točke u izvoru vala: y = yo sin t x y = yo sin (t-t') , , ,

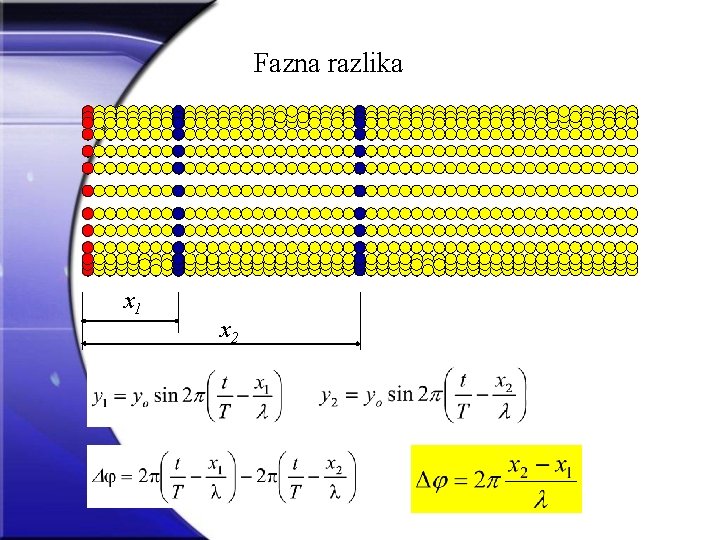
Fazna razlika x 1 x 2

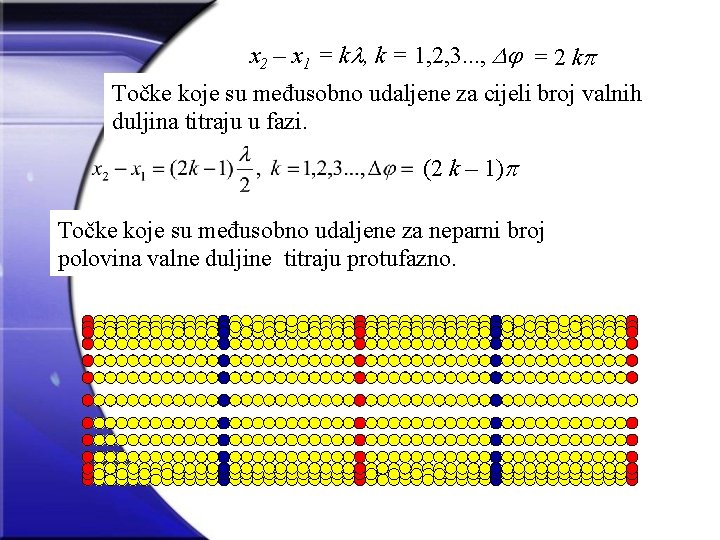
x 2 – x 1 = k , k = 1, 2, 3. . . , = 2 k Točke koje su međusobno udaljene za cijeli broj valnih duljina titraju u fazi. (2 k – 1) Točke koje su međusobno udaljene za neparni broj polovina valne duljine titraju protufazno.

Zadatak: Iz jednadžbe vala: odredite: a) amplitudu y = 0, 05 m b) kružnu frekvenciju, frekvenciju i period = 2 s-1 = 2 f T= 1 s f = 1 Hz c) brzinu i smjer širenje vala v = f = 2 m 1 Hz = 2 m v = 2 m s-1 udesno

d) najveću brzinu titranja i najveću akceleraciju titranja čestica sredstva kojim se val širi vo = yo = 2 s-1 0, 05 m vo = 0, 1 m s-1 ao = - 2 yo = - (2 s-1)2 0, 05 m ao = - 0, 2 2 m s-2 e) faznu razliku titranja dviju čestica koje su međusobno udaljene 1, 5 m. x = x 2 – x 1 = 1, 5 m

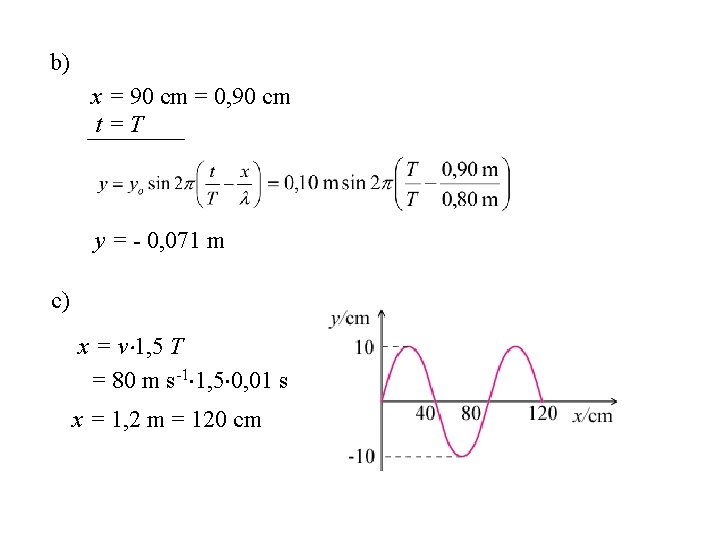
Primjer: Harmonijski val amplitude 10 cm širi se brzinom 80 m s-1. Dvije čestice sredstva koje leže na istom pravcu širenja vala međusobno su udaljene 20 cm i titraju s faznom razlikom 90 o. a) Kako glasi jednadžba vala? b) Kolika je elongacija čestice koja se nalazi 90 cm od izvora u trenutku kada je u izvoru napravljen potpuni titraj? c) Nacrtajmo sliku vala nakon što je u izvoru napravljeno 1, 5 titraja. Rješenje: yo = 10 cm = 0, 10 m v = 80 m s-1 x = 20 cm = 0, 20 m = 90 o a) T = 0, 01 s = 0, 80 m

b) x = 90 cm = 0, 90 cm t=T y = - 0, 071 m c) x = v 1, 5 T = 80 m s-1 1, 5 0, 01 s x = 1, 2 m = 120 cm

Refleksija longitudinalnog vala Impulsi sile longitudinalni poremećaj u elastičnom štapu predaja neke energije koja se širi štapom Što se događa s energijom kada nastali ravni val stigne na kraj štapa? Energija može prijeći na neko drugo sredstvo ili se vraća natrag u štap: tada dolazi do djelomične ili potpune refleksije longitudinalnog vala pomaka na kraju štapa. Ako je na kraju štapa vakuum, val se ne može dalje prenijeti (jer nema sredstva) te dolazi do totalne refleksije vala i energije u savršeno elastičnom štapu. Razlikujemo dva granična slučaja refleksije: a) kraj štapa je slobodan b) kraj štapa je nepomičan. Interferencija = Zbrajanje valova (početni + reflektirani)

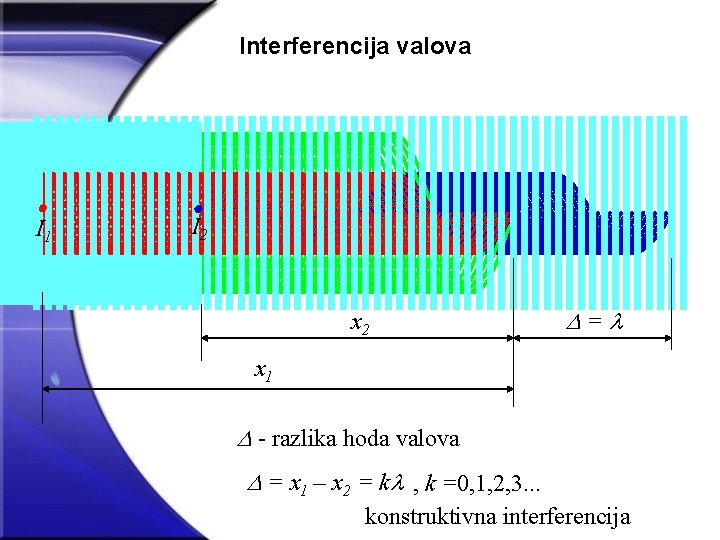
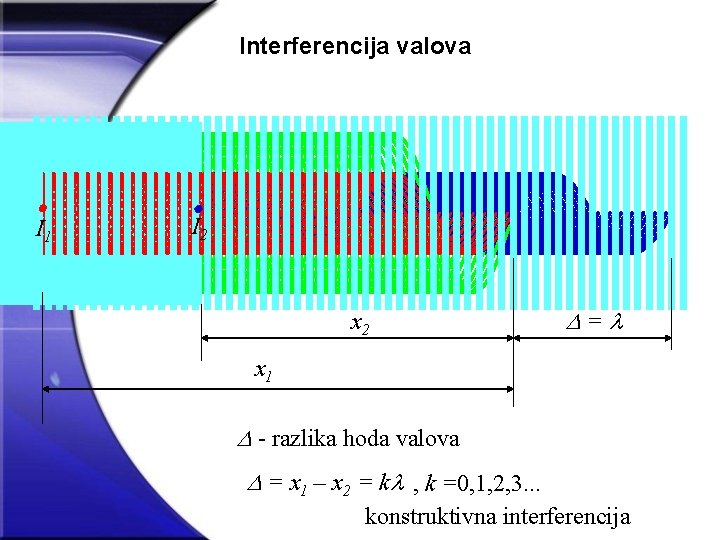
Interferencija valova I 1 I 2 x 2 = x 1 - razlika hoda valova = x 1 – x 2 = k , k =0, 1, 2, 3. . . konstruktivna interferencija

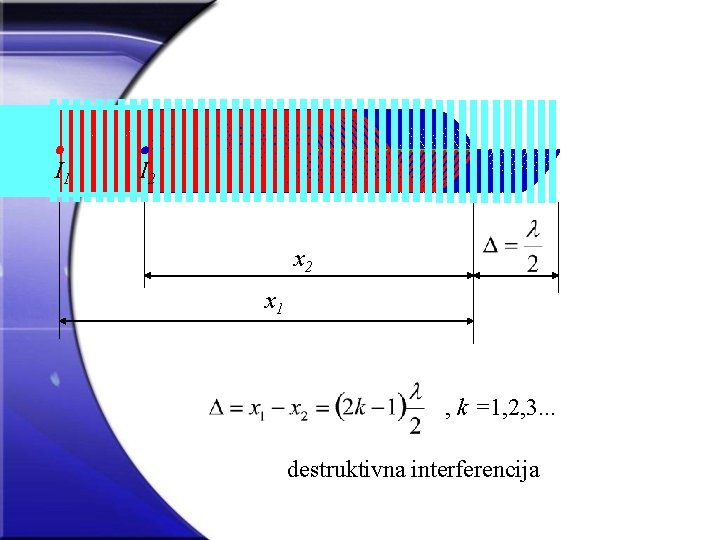
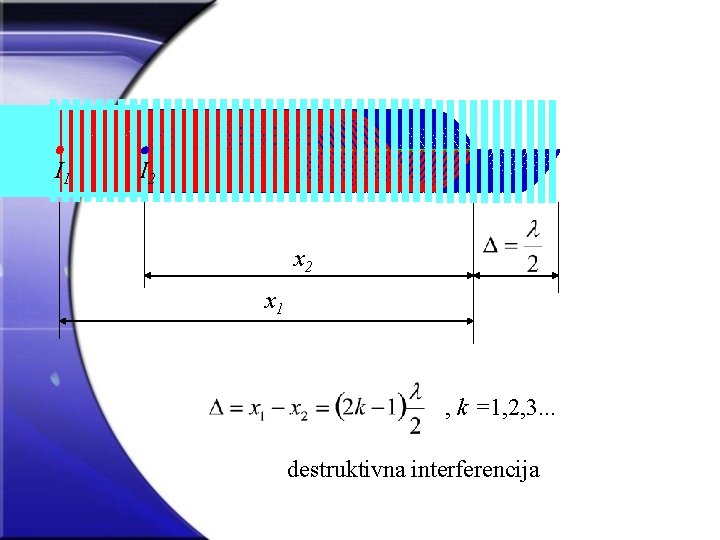
I 1 I 2 x 1 , k =1, 2, 3. . . destruktivna interferencija

Refleksija longitudinalnog vala pomaka na slobodnom kraju Neka je štap položen uzduž osi x tako da je slobodan kraj štapa smješten u ishodištu.

Refleksija longitudinalnog vala pomaka na slobodnom kraju Neka je štap položen uzduž osi x tako da je slobodan kraj štapa smješten u ishodištu. Na slobodnom kraju, dok traje refleksija, čestice (sloj) štapa će biti podvrgnute obim gibanjima, pa će pomak na slobodnom kraju biti: Rubni uvjet - kako na slobodni kraj ne djeluje izvana nikakva sila, tanki krajnji sloj nije deformiran (Du = 0), pa vrijedi:

Refleksija longitudinalnog vala pomaka na slobodnom kraju 2 U ishodištu, x = 0 Na rubu štapa, gdje se događa refleksija, f = j Pri refleksiji na slobodnom kraju oblik vala ostaje nepromijenjen. povećanje volumena ili dilatacija zgušnjenje ili kompresija Dilatacija se reflektira na slobodnom kraju u kompresiju i obratno.

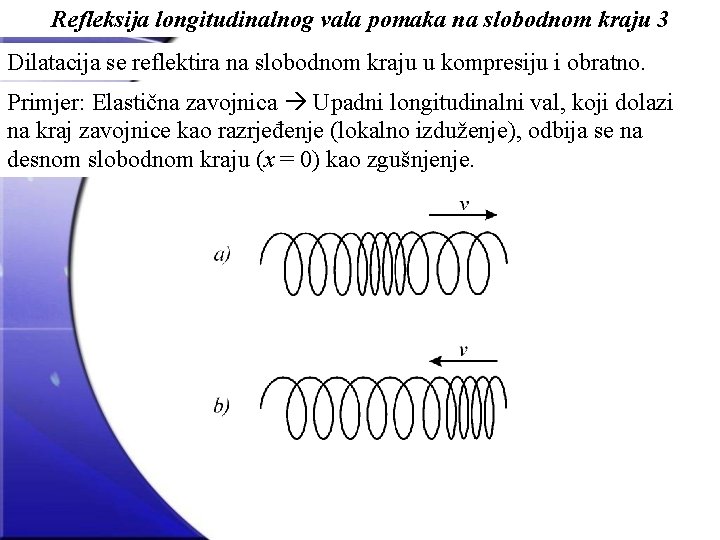
Refleksija longitudinalnog vala pomaka na slobodnom kraju 3 Dilatacija se reflektira na slobodnom kraju u kompresiju i obratno. Primjer: Elastična zavojnica Upadni longitudinalni val, koji dolazi na kraj zavojnice kao razrjeđenje (lokalno izduženje), odbija se na desnom slobodnom kraju (x = 0) kao zgušnjenje.

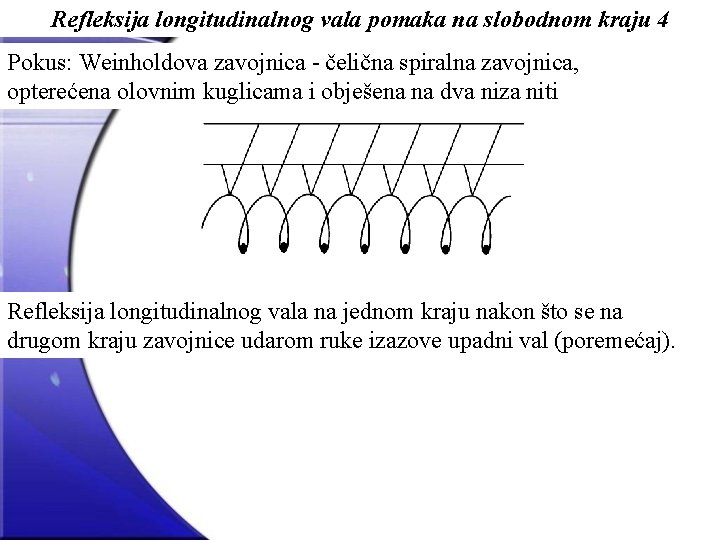
Refleksija longitudinalnog vala pomaka na slobodnom kraju 4 Pokus: Weinholdova zavojnica - čelična spiralna zavojnica, opterećena olovnim kuglicama i obješena na dva niza niti Refleksija longitudinalnog vala na jednom kraju nakon što se na drugom kraju zavojnice udarom ruke izazove upadni val (poremećaj).

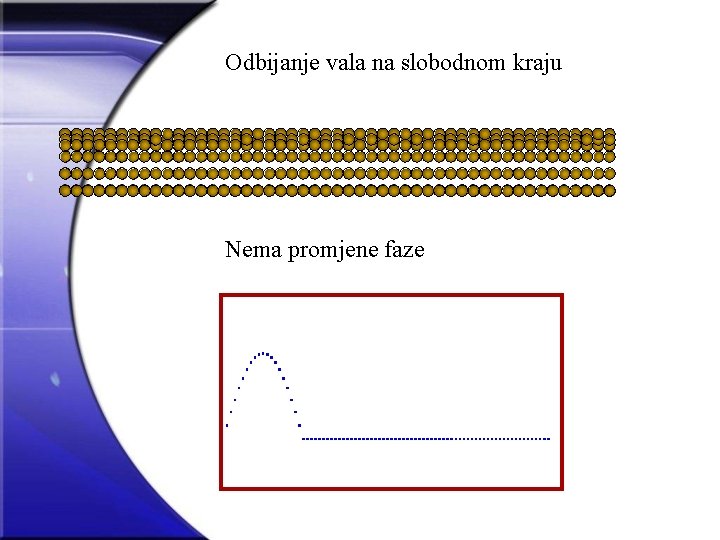
Odbijanje vala na slobodnom kraju Nema promjene faze

Refleksija longitudinalnog vala pomaka na slobodnom kraju 5 Zaključak: Za sinusni longitudinalni val, pri refleksiji vala na slobodnom kraju, nema promjene u fazi. upadni val reflektirani val Upadni i odbijeni sinusni val imaju istu fazu u ravnini refleksije (ta ravnina prolazi ishodištem i okomita je na os x).

Refleksija longitudinalnog vala pomaka na nepomičnom kraju štapa Nepomičan kraj Energija upadnog vala ne može se prenijeti preko kraja štapa jer je kraj učvršćen, ne može se pomicati. refleksija Rubni uvjeti: u = 0, za x = 0 (pomak sloja na kraju štapa u ishodištu)

Refleksija longitudinalnog vala pomaka na nepomičnom kraju štapa Nepomičan kraj Energija upadnog vala ne može se prenijeti preko kraja štapa jer je kraj učvršćen, ne može se pomicati. refleksija Rubni uvjeti: u = 0, za x = 0 (pomak sloja na kraju štapa u ishodištu) Nakon refleksije na nepomičnom kraju funkcija vala ostaje ista ali mijenja predznak, tj. vrijedi f = - j: Uz oznake: Za x = 0 Na nepomičnom kraju štapa kompresiji (zgušnjenju) upadnog vala nakon refleksije odgovara kompresija odbijenog vala, odnosno dilatacija (izduženje) upadnog vala daje dilataciju odbijenog vala.

Refleksija longitudinalnog vala pomaka na nepomičnom kraju štapa 2 Pokus: Jedan kraj Weinholdove zavojnice pričvrstimo (npr. hvataljkom na stalku), a na drugom kraju zavojnice rukom se izvodi poremećaj; ovaj se prenosi kao longitudinalni val i na nepomičnom kraju zavojnice se zapaža kako je jednako zgušnjenje, odnosno dilatacija, kod upadnog i odbijenog vala. Značenje promjene predznaka valne funkcije (uz rubni uvjet) za sinusni val? Ima značenje «skoka» u fazi za p nakon refleksije. (Kada se za funkcije sinus i cosinus kut npr. iz prvog kvadranta poveća za p ili 180 o , onda funkcija zadržava istu vrijednost, ali sa suprotnim predznakom. )

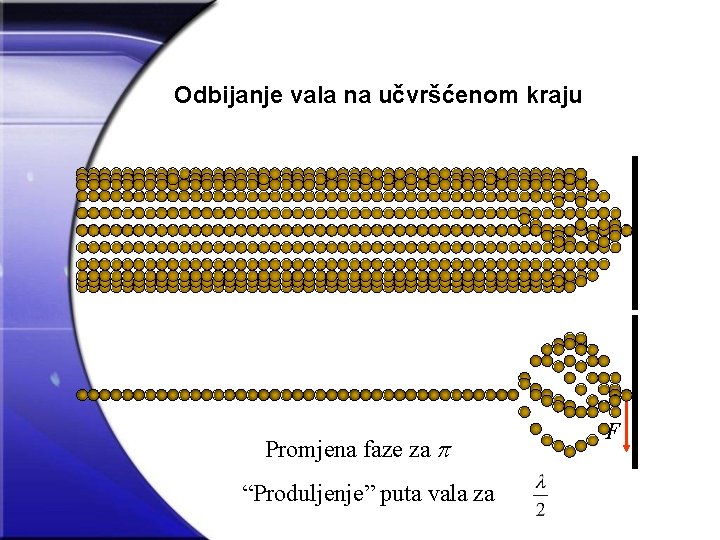
Odbijanje vala na učvršćenom kraju Promjena faze za “Produljenje” puta vala za F

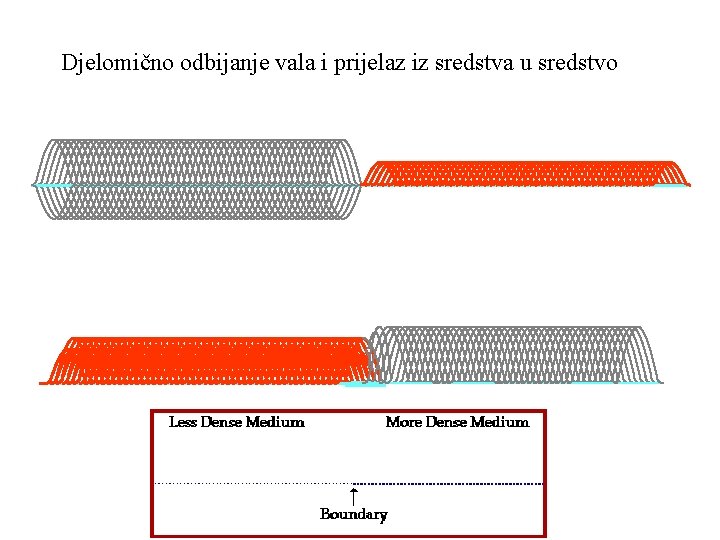
Djelomično odbijanje vala i prijelaz iz sredstva u sredstvo

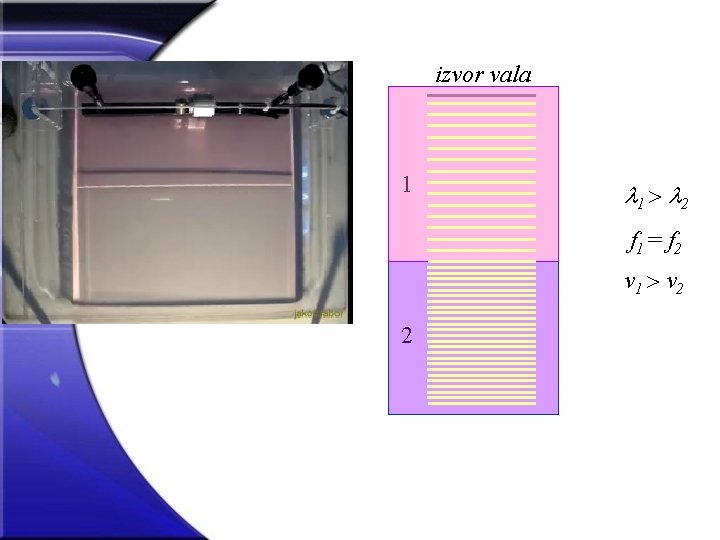
izvor vala 1 1 2 f 1 = f 2 v 1 v 2 2

Zadatak: Zvuk valne duljine 77 cm prelazi iz zraka u vodu. Kolika je valna duljina zvuka u vodi? Za brzinu zvuka u zraku uzmite 340 m s-1, a u vodi 1500 m s-1. Rješenje: z = 77 cm = 0, 77 m vz = 340 m s-1 vv = 1500 m s-1 fz = f v v = 3, 4 m

Primjer: Točkasti izvor zvuka frekvencije 3400 Hz nalazi se 30 cm iznad površine stola. U točku T, koja je 80 cm udaljena od izvora i na jednakoj visini iznad stola kao i izvor, dolazi val izravno iz izvora i val odbijen od površine stola. Što će biti rezultat interferencije izravnog i odbijenog vala u toj točki? Brzina zvuka u zraku je 340 m s-1? Rješenje: izvor T f = 3400 Hz d x 1 = d = 0, 80 m h h = 30 cm d = 80 cm v = 340 m s-1 x = ? v= f = 0, 1 m x 2= 1, 05 m x = x 2 – x 1 x = 1, 05 m – 0, 80 m x = 0, 25 m

Zadatak: Cijev polukružnog oblika svojim je krajevima spojena s krajevima ravne cijevi kako prikazuje slika. Duljina je ravne cijevi 2 m. Na otvoru A je mali zvučnik koji emitira zvuk frekvencije 1800 Hz. Hoćemo li uhom na otvoru B registrirati maksimalnu ili minimalnu jakost zvuka? Brzina je zvuka 342 m s-1. Rješenje: d=2 m f = 1800 Hz v = 342 m s-1 x = ? x 1 = d = 2 m = 0, 19 m B d x = x 2 – x 1 x = 3, 14 m – 2 m x = 1, 14 m x 2 = 3, 14 m A =6 x = 6

Stojni longitudinalni valovi Do sada: - promatrali smo uglavnom kratkotrajne valove, pomake ili pulseve - refleksiju na kraju štapa gledamo kao superpoziciju dva gibanja Promatramo dva ravna longitudinalna sinusna vala jednakih perioda i amplituda, jednakih brzina po iznosu ali suprotnog smjera u homogenom izotropnom elastičnom sredstvu. Neka se valovi gibaju po osi x; ishodište sustava odabiremo u točki gdje su obje faze jednake. upadni val reflektirani val Superpozicija daje:

Stojni longitudinalni valovi 2 Rezultantno gibanje Produkt dviju cosinusnih funkcija od kojih jedna faza ovisi samo o vremenu a druga samo o prostoru. Simbolički pišemo: gdje amplituda pomaka a ovisi samo o apscisi x : Sve točke u sredstvu imaju istu vremensku fazu wt Ovakvu vrstu gibanja, zovemo stojnim (ili stacionarnim) valom, s pripadnom valnom funkcijom u.

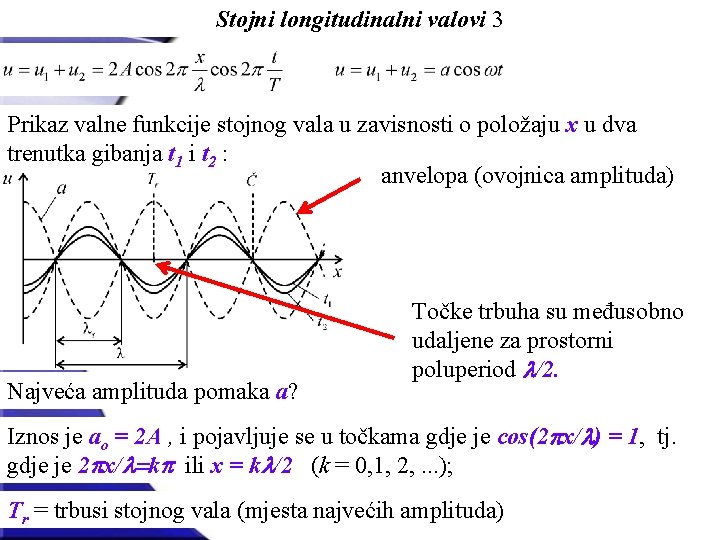
Stojni longitudinalni valovi 3 Prikaz valne funkcije stojnog vala u zavisnosti o položaju x u dva trenutka gibanja t 1 i t 2 : anvelopa (ovojnica amplituda) Najveća amplituda pomaka a? Točke trbuha su međusobno udaljene za prostorni poluperiod l/2. Iznos je ao = 2 A , i pojavljuje se u točkama gdje je cos(2 px/l) = 1, tj. gdje je 2 px/l=kp ili x = kl/2 (k = 0, 1, 2, . . . ); Tr = trbusi stojnog vala (mjesta najvećih amplituda)

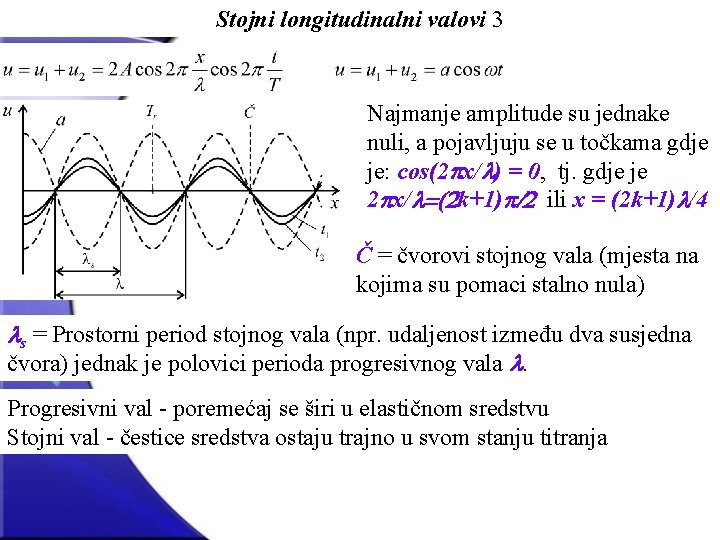
Stojni longitudinalni valovi 3 Najmanje amplitude su jednake nuli, a pojavljuju se u točkama gdje je: cos(2 px/l) = 0, tj. gdje je 2 px/l=(2 k+1)p/2 ili x = (2 k+1)l/4 Č = čvorovi stojnog vala (mjesta na kojima su pomaci stalno nula) ls = Prostorni period stojnog vala (npr. udaljenost između dva susjedna čvora) jednak je polovici perioda progresivnog vala l. Progresivni val - poremećaj se širi u elastičnom sredstvu Stojni val - čestice sredstva ostaju trajno u svom stanju titranja

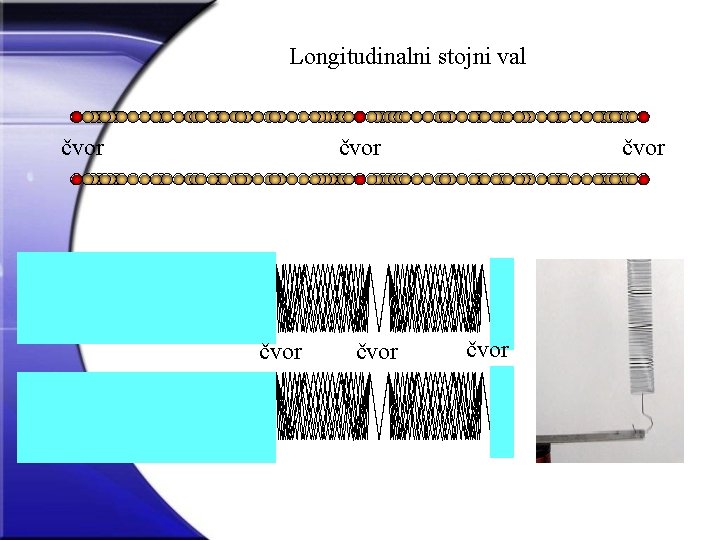
Longitudinalni stojni val čvor čvor

Stojni longitudinalni valovi 4

Stojni longitudinalni valovi 4

Stojni longitudinalni valovi 4 Stojni val – nastaje kao zbroj (interferencija) dvaju valova jednake amplitude i jednake valne duljine, koji na istom pravcu putuju jedan nasuprot drugom. Primjer: Upadni progresivni val reflektira se na kraju sredstva i zbroji s dolazećim upadnim valom. Primjer: Refleksija na nepomičnom kraju štapa nepomičan kraj mora biti čvor stojnog vala (čvor ima nultu amplitudu, tj. nema pomaka, pa vrijedi: u = u 1 + u 2 = 0)

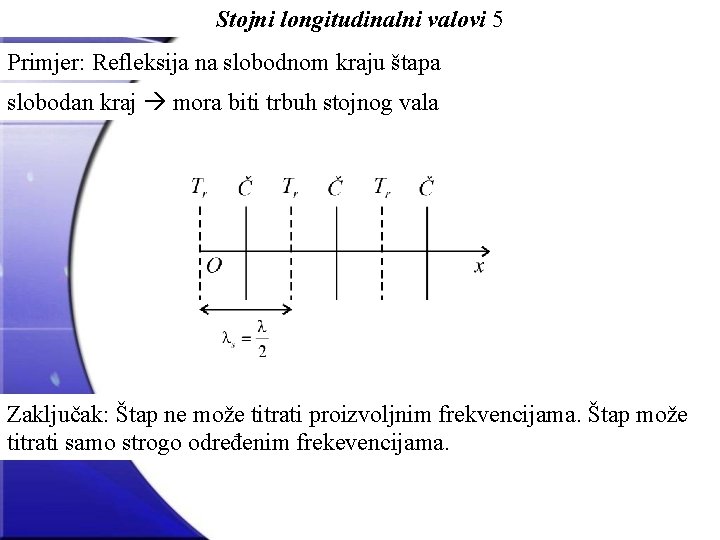
Stojni longitudinalni valovi 5 Primjer: Refleksija na slobodnom kraju štapa slobodan kraj mora biti trbuh stojnog vala Zaključak: Štap ne može titrati proizvoljnim frekvencijama. Štap može titrati samo strogo određenim frekevencijama.

Longitudinalno titranje štapa duljine L štap pobudimo ga nizom impulsa harmoničke sile u longitudinalnom smislu, tj. uzdužno, u štapu će se pojaviti sinusni val pomaka Na krajevima štapa valovi se reflektiraju nastaje sinusni stojni (stacionarni) val Način titranja zavisit će o tome jesu li krajevi štapa slobodni ili učvršćeni Frekvencije slobodnog titranja štapa su diskretne; moguće su samo neke frekvencije (ovisno o rubnim uvjetima na oba kraja štapa).

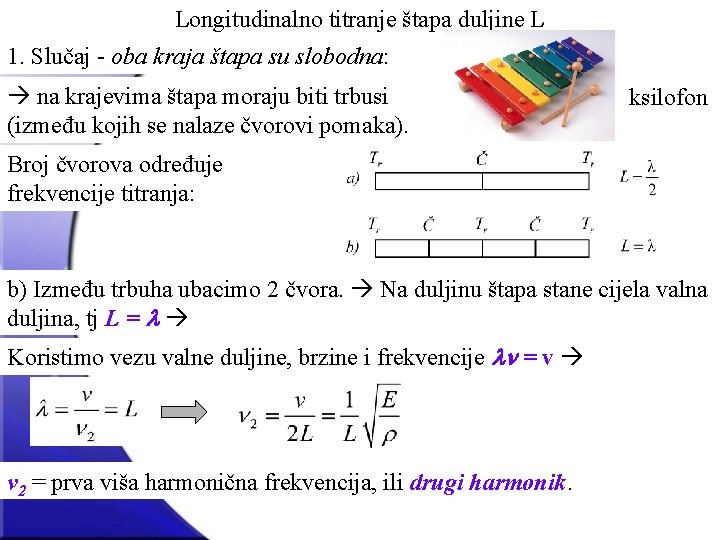
Longitudinalno titranje štapa duljine L 1. Slučaj - oba kraja štapa su slobodna: na krajevima štapa moraju biti trbusi (između kojih se nalaze čvorovi pomaka).

Longitudinalno titranje štapa duljine L 1. Slučaj - oba kraja štapa su slobodna: na krajevima štapa moraju biti trbusi (između kojih se nalaze čvorovi pomaka). Broj čvorova određuje frekvencije titranja: a) Između trbuha samo 1 čvor. Na duljinu štapa stane samo pola valne duljine, tj L = l/2 l = 2 L Koristimo vezu valne duljine, brzine i frekvencije ln = v v 1 = najmanja frekvencija kojom štap može slobodno titrati; tzv. osnovna frekvencija promatranog sustava (štapa), ili prvi harmonik.

Longitudinalno titranje štapa duljine L 1. Slučaj - oba kraja štapa su slobodna: na krajevima štapa moraju biti trbusi (između kojih se nalaze čvorovi pomaka). ksilofon Broj čvorova određuje frekvencije titranja: b) Između trbuha ubacimo 2 čvora. Na duljinu štapa stane cijela valna duljina, tj L = l Koristimo vezu valne duljine, brzine i frekvencije ln = v v 2 = prva viša harmonična frekvencija, ili drugi harmonik.

Longitudinalno titranje štapa duljine L 1. Slučaj - oba kraja štapa su slobodna: na krajevima štapa moraju biti trbusi (između kojih se nalaze čvorovi pomaka). c) Između trbuha stavimo 3 čvora. Na duljinu štapa stane 1, 5 valne duljine, tj L = 3 l/2 l = 2 L/3 Koristimo vezu valne duljine, brzine i frekvencije ln = v Nakon trećeg harmonika slično bi dobili četvrti, itd. Za harmonike vrijedi odnos: Frekvencije s kojima može titrati slobodan štap odnose se kao cijeli brojevi.

Longitudinalno titranje štapa duljine L 2. slučaj - oba kraja štapa su nepomična na krajevima štapa moraju biti čvorovi (između kojih može biti jedan ili više trbuha pomaka. )

Longitudinalno titranje štapa duljine L 2. slučaj - oba kraja štapa su nepomična na krajevima štapa moraju biti čvorovi (između kojih može biti jedan ili više trbuha pomaka. ) a) Između čvorova samo 1 trbuh. Na duljinu štapa stane samo pola valne duljine, tj L = l/2 l = 2 L Koristimo vezu valne duljine, brzine i frekvencije ln = v Nakon prvog harmonika slično bi dobili drugi, treći, itd.

Primjer: Napeta nit duga 2 m učvršćena je na oba kraja. Pri titranju frekvencijom 240 Hz na niti se opaža pet čvorova uključujući i one na krajevima niti. a) Kolika je brzina vala po niti? b) Kolika je osnovna frekvencija niti? Rješenje: l=2 m f = 240 Hz a) v = ? v = f = 1 m 240 Hz , v = 240 m s-1 b) f = ? f 1= 60 Hz

Longitudinalno titranje štapa duljine L 3. slučaj – jedan kraj štapa je nepomičan, drugi slobodan na slobodnom kraju štapa mora biti trbuh, a na krutom kraju čvor

Longitudinalno titranje štapa duljine L 3. slučaj – jedan kraj štapa je nepomičan, drugi slobodan na slobodnom kraju štapa mora biti trbuh, a na krutom kraju čvor a) Između krajeva štapa nema ni trbuha ni čvora Na duljinu štapa stane samo četvrtina valne duljine, tj L = l/4 l = 4 L v 1 = najmanja frekvencija kojom štap može slobodno titrati; tzv. osnovna frekvencija promatranog sustava (štapa), ili prvi harmonik.

Zadatak 1: Metalni štap duljine 60 cm jednim je krajem učvršćen za zid. Slobodni kraj štapa pobuđujemo harmonijski frekvencijom 5500 Hz. Na štapu osim čvora uza zid opažamo još 5 čvorova. Koliki je Youngov modul elastičnosti štapa, ako je njegova gustoća 11000 kg m-3? Rješenje: l = 60 cm = 0, 60 m f = 5500 Hz = 11000 kg m-3 E=? E= v 2 E = 1, 6 1010 N m-2 l

Longitudinalno titranje štapa duljine L 3. slučaj – jedan kraj štapa je nepomičan, drugi slobodan na slobodnom kraju štapa mora biti trbuh, a na krutom kraju čvor harmonika b) Između krajeva štapa jedan čvor i jedan trbuh Na duljinu štapa stane tri četvrtine valne duljine, tj L = 3 l/4 l = 4 L/3 Slično se dobiju frekvencije samo neparnih harmonika te vrijede odnosi:

Transverzalni valovi Promatramo savršeno elastičnu nit (žicu), zanemarive težine, u stanju ravnoteže. Žicu pravocrtno zateže napetost. Pod utjecajem vanjskih sila (npr. udarac), nit (žica ) se može deformirati. Promatramo mali element niti udarac (okomit na nit) transverzalni pomak na niti Promatramo mali pomak, tako da se napetost niti N ne mijenja kut žice prema osi x (na kojoj leži nit) je tada mali.

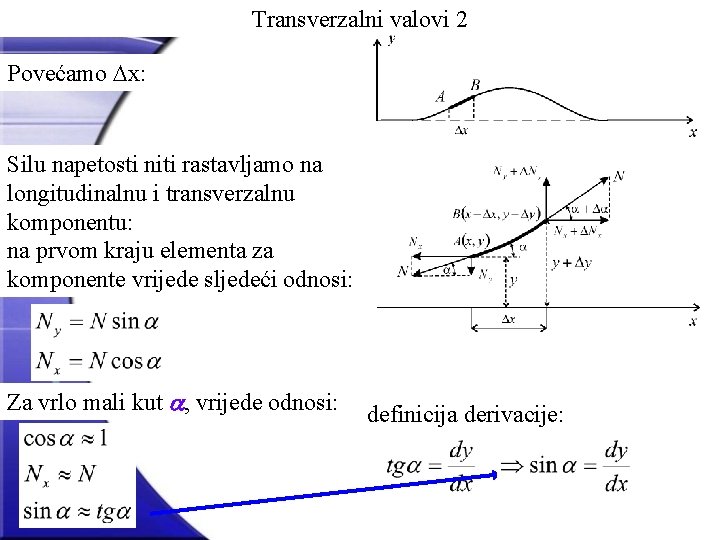
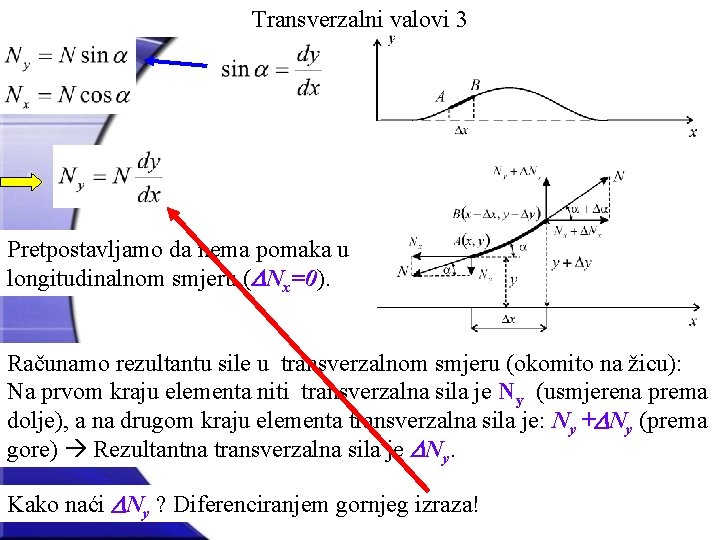
Transverzalni valovi 2 Povećamo Dx: Silu napetosti niti rastavljamo na longitudinalnu i transverzalnu komponentu: na prvom kraju elementa za komponente vrijede sljedeći odnosi: Za vrlo mali kut a, vrijede odnosi: definicija derivacije:

Transverzalni valovi 3 Pretpostavljamo da nema pomaka u longitudinalnom smjeru (DNx=0). Računamo rezultantu sile u transverzalnom smjeru (okomito na žicu): Na prvom kraju elementa niti transverzalna sila je Ny (usmjerena prema dolje), a na drugom kraju elementa transverzalna sila je: Ny +DNy (prema gore) Rezultantna transverzalna sila je DNy. Kako naći DNy ? Diferenciranjem gornjeg izraza!

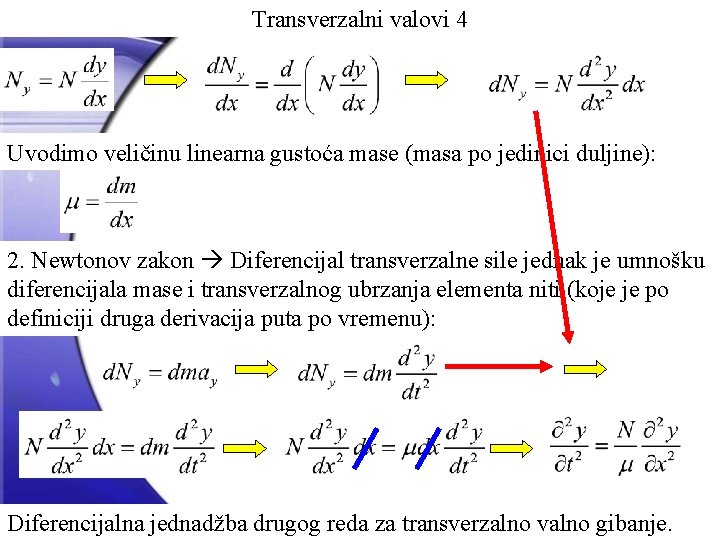
Transverzalni valovi 4 Uvodimo veličinu linearna gustoća mase (masa po jedinici duljine): 2. Newtonov zakon Diferencijal transverzalne sile jednak je umnošku diferencijala mase i transverzalnog ubrzanja elementa niti (koje je po definiciji druga derivacija puta po vremenu): Diferencijalna jednadžba drugog reda za transverzalno valno gibanje.

Transverzalni valovi 5 Dimenzija N/m ? Isti oblik kao i kod longitudinalnog titranja. Rješenje jednadžbe za y (transverzalni pomak elementa niti ili čestice elastičnog sredstva) je funkcija poznatog oblika: Uzimamo također oznake, slično prethodnima: y 1 - funkcija vala koji se širi u pozitivnom smjeru osi x y 2 - funkcija vala koji se širi u negativnom smjeru osi x

Transverzalni valovi 6 Slično, kao u prethodnom poglavlju, rješenja: Slikovita usporedba longitudinalnih i transverzalnih pomaka slojeva u elastičnom sredstvu:

- linearna gustoća , F – sila napetosti Zadatak: Elastično uže duljine 30 m i mase 6 kg napeto je vješanjem utega. Oštrim udarcem izazovemo na jednom kraju užeta transverzalni poremećaj, koji se nakon 1, 12 s vrati na mjesto gdje je nastao. Kolika je masa utega koji napinje uže? Rješenje: l = 30 m m 1 = 6 kg t = 1, 12 s m 2 = ? l m 2 = 58, 5 kg

Refleksija transverzalnog vala Slično, kao u prethodnom poglavlju, za refleksiju transverzalnog pulsa na nepomičnom kraju, općenito vrijedi također rubni uvjet: y = 0 f = -j Refleksija transverzalnog vala zbiva se uz promjenu predznaka valne funkcije. Pokus – Transverzalni puls na napetoj gumenoj cijevi na nepomičnom kraju daje odbijeni val s amplitudom protivnog predznaka upadnom valu.

Transverzalni stojni sinusni valovi - nastaju pribrajanjem (superpozicijom) valnih gibanja, kao za valne funkcije iz jednadžbi y = y 1 + y 2 (npr. upadni i odbijeni kosinusni val). Kao kog longitudinalnih valova, razvijanjem funkcija kosinus dobije se već poznati oblik rezultantnog stojnog vala: a = amplituda stojnog vala

Interferencija valova I 1 I 2 x 2 = x 1 - razlika hoda valova = x 1 – x 2 = k , k =0, 1, 2, 3. . . konstruktivna interferencija

I 1 I 2 x 1 , k =1, 2, 3. . . destruktivna interferencija

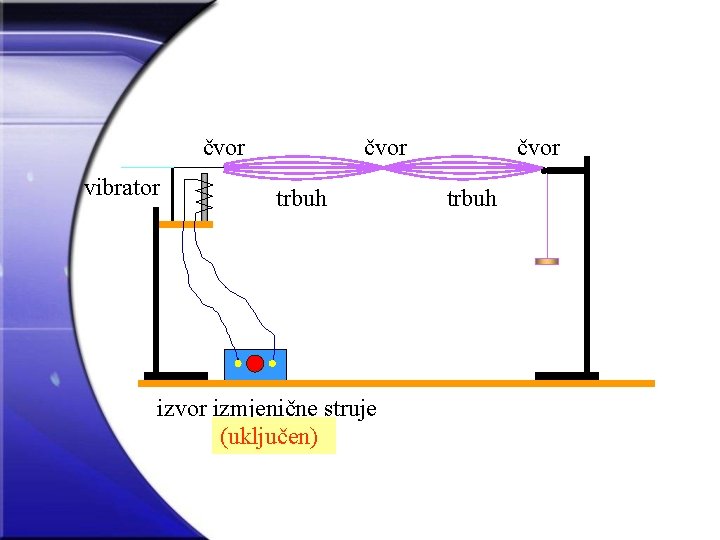
čvor vibrator čvor trbuh izvor izmjenične struje (isključen) (uključen) čvor trbuh

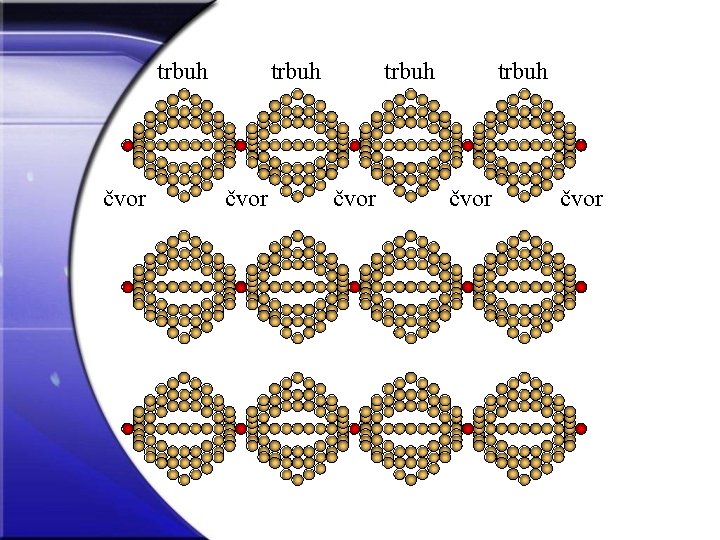
trbuh čvor čvor

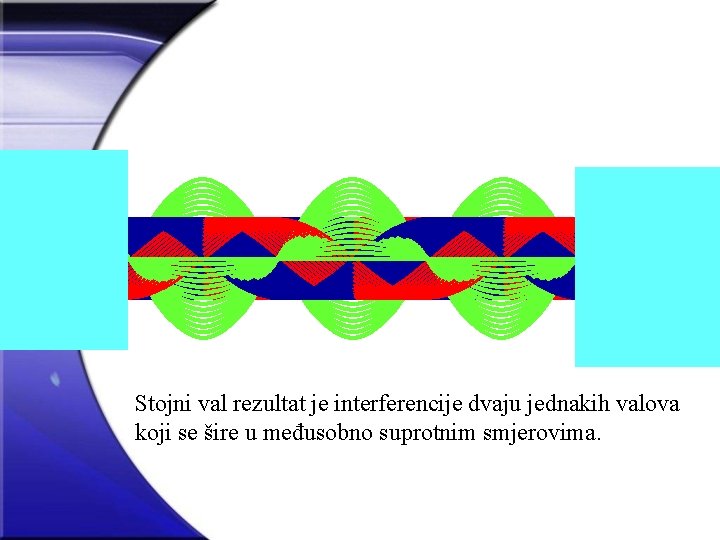
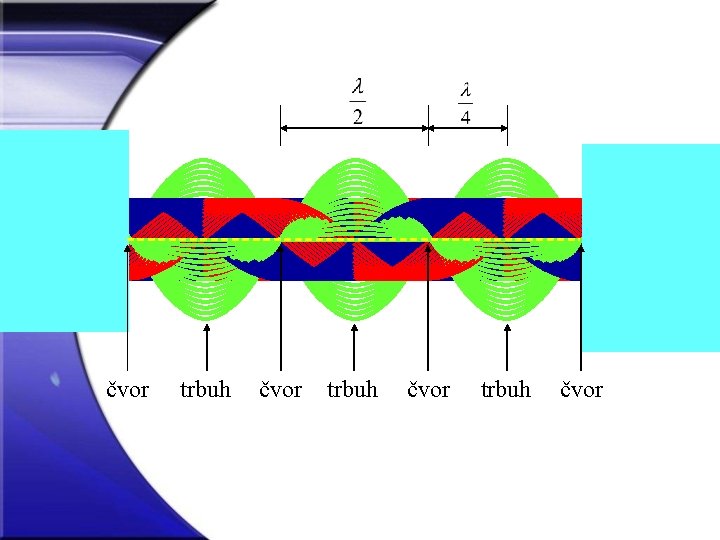
Stojni val rezultat je interferencije dvaju jednakih valova koji se šire u međusobno suprotnim smjerovima.

čvor trbuh čvor

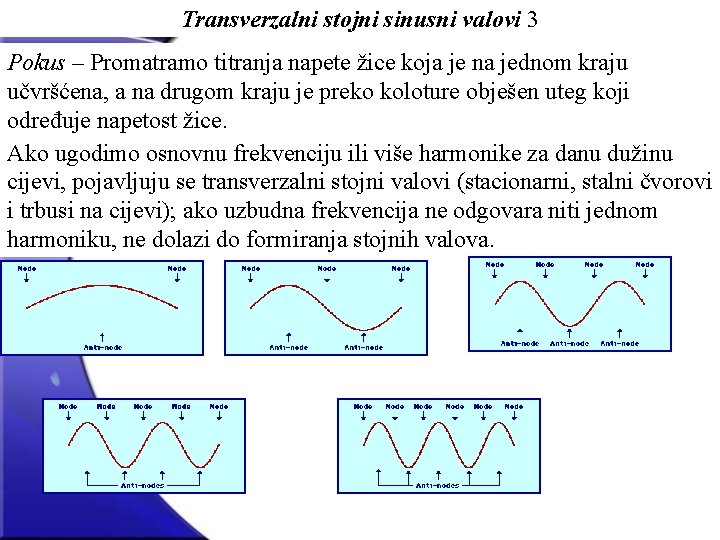
Transverzalni stojni sinusni valovi 2 Primjer transverzalnih stojnih valova: titranje napete žica učvršćena na oba kraja čvorovi a) samo jedan trbuh i dva čvora b) dva trbuha i tri čvora daju drugi harmonik: Za tri trbuha na žici slično dobijemo frekvenciju trećeg harmonika. Zaključak: Harmonici čine potpuni niz cijelih brojeva, što se naziva i Galileijev zakon za žice koje titraju: n = kn ; k=1, 2, 3, …

Transverzalni stojni sinusni valovi 3 Pokus – Promatramo titranja napete žice koja je na jednom kraju učvršćena, a na drugom kraju je preko koloture obješen uteg koji određuje napetost žice. Ako ugodimo osnovnu frekvenciju ili više harmonike za danu dužinu cijevi, pojavljuju se transverzalni stojni valovi (stacionarni, stalni čvorovi i trbusi na cijevi); ako uzbudna frekvencija ne odgovara niti jednom harmoniku, ne dolazi do formiranja stojnih valova.

Složena titranja elastičnog sredstva Do sada: uzbudimo sustav, npr. napetu čeličnu žicu ili gumenu cijev, na jednom kraju nastane transverzalni stojni val Što se događa ako i na drugom kraju istovremeno uzbudimo sustav, npr. na neki drugi harmonik? Stvori se poremećaj koji odgovara zbroju transverzalnih pomaka y 1 i y 2 stojnih valova danog sustava (žice). Primjer: Najjednostavniji slučaj nastupa kad je sustav pobuđen na prvi i drugi harmonik.

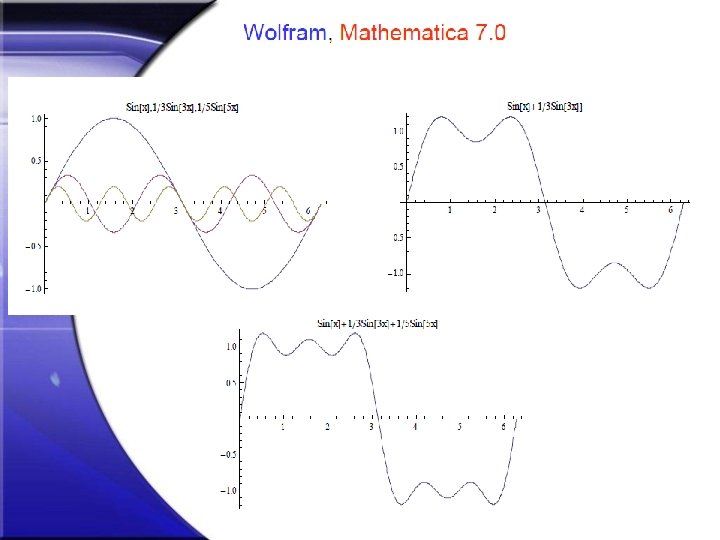
Složena titranja elastičnog sredstva 2 Općenito: Titranje sustava može biti puno složenije od navedenog primjera s dva harmonika; (npr. elastični štapovi mogu titrati i transverzalno kada su pričvršćeni na jednom kraju; titranje elastične tanke ploče ili membrane promatra se u dvije dimenzije, i dr. ) Periodična složena valna gibanja možemo uglavnom uspješno prikazati kao zbroj harmoničkih valova, što se izvodi postupkom harmoničke ili Fourierove analize. Fourierova se analiza izvodi za periodične funkcije tako da se neka funkcija f(t), s periodom T, rastavi u zbroj sinusnih i kosinusnih funkcija. Naime, periodična funkcija f(t) = f(t + T) može se prikazati pomoću beskonačnog Fourierovog reda, kako slijedi: f(t) = ao + a 1 cos t + a 2 cos 2 t +. . . + am cos m t +. . . + bo + b 1 sin t + b 2 sin 2 t + + bn sin n t +. . .

Složena titranja elastičnog sredstva 3 Primjer. Zadana je periodična funkcija: f(t) = 1 , za 0 < t < T/2 ; f(t) = -1 , za T/2 < t < T. Aproksimirajmo je pomoću Fourierove analize. … koeficijenti am iščezavaju, kao i parni koeficijenti b, dok su neparni: b 3 = 4/3, b 5 = 4/5, . . . , itd