Observing the Clustering of Matter and Galaxies History

Observing the Clustering of Matter and Galaxies History: 1920 - Lick Galaxy Map : galaxies in and around the local group are not distributed randomly 1950 -1970: Shane and Wirtanen – – made maps of the (projected) galaxy distribution Non-random distribution on small to large scales 1980 -1990: Geller, Huchra and many others – – made maps of the 3 D galaxy distribution Depth variable redshift (not quite distance) Cf. A Slice with Great Wall 2000+: 2 DF Redshift Survey / SDSS – 100, 000 galaxies with spectra (Literature: e. g. Peacock: Cosmological Physics, p 500 -509) Vatican 2003 Lecture 20 HWR

State-of-the-Art Example: 2 DFRS (from Peacock et al 2002) Star-Forming Galaxies Red Galaxies Vatican 2003 Lecture 20 HWR

Describing the Statistics of Clustering • There is no unique way to describe clustering! – Need to describe the degree of clustering not the particular configuration. – Isotropy: clustering = f(x, y, z) f(r) • Often-used measures are: • Angular or real-space correlation function • Genus curve – Smooth galaxies on different scales – Which fraction of the volume is filled by curves of a given over-/under-density • Counts-in cells • Main practical problems/issues: – Complicated search volumes – Finite number of tracers – Redshift space distortion Vatican 2003 Lecture 20 HWR

Correlation Functions • Excess probability of finding one galaxy (mass element) “near” another galaxy: - for a random (uniform) distribution: d. P = n d. V n: mean number density - a clustered distribution can be (incompletely) described by: d. P(r) = n [1 + (r)] d. V, where d. P is the probability of finding a second object near an object at r = 0 (r): two-point (or, auto-) correlation function Note: (r) = < (x) (x+r) >, where (x) is the fractional over/under-density - to account for translation and rotation invariance (cosmological principle) often the Fourier transform is used P(k) | k|2 = (r) eikr d 3 r P(k): power spectrum - practical estimation: Vatican 2003 Lecture 20 HWR

• If no redshifts (distances) are available, one can define the angular correlation function d. P ( ) = n (1 + w( ) ) d Note: • understanding the sampling window function of a survey is crucial • usually one is measuring the correlation of tracers Vatican 2003 Lecture 20 HWR

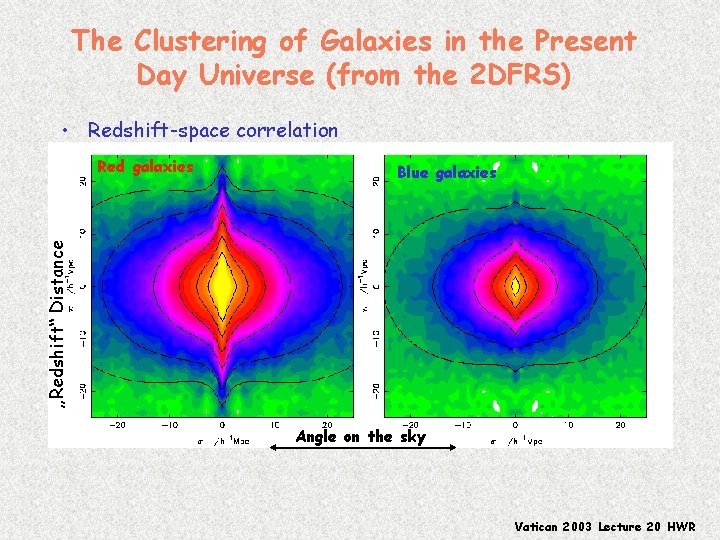
The Clustering of Galaxies in the Present Day Universe (from the 2 DFRS) • Redshift-space correlation Blue galaxies „Redshift“ Distance Red galaxies Angle on the sky Vatican 2003 Lecture 20 HWR

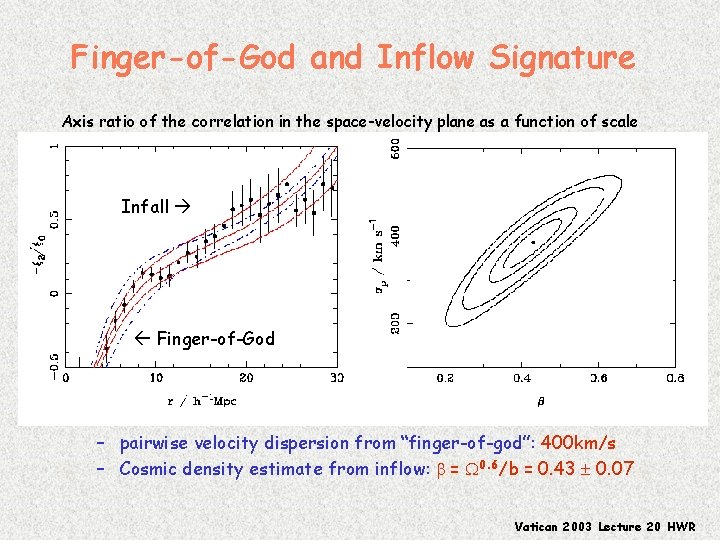
Finger-of-God and Inflow Signature Axis ratio of the correlation in the space-velocity plane as a function of scale Infall Finger-of-God – pairwise velocity dispersion from “finger-of-god”: 400 km/s – Cosmic density estimate from inflow: b = 0. 6/b = 0. 43 0. 07 Vatican 2003 Lecture 20 HWR

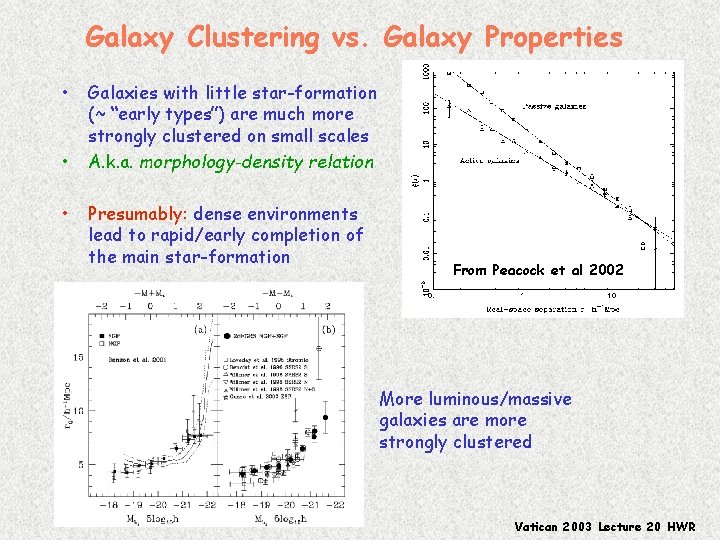
Galaxy Clustering vs. Galaxy Properties • • • Galaxies with little star-formation (~ “early types”) are much more strongly clustered on small scales A. k. a. morphology-density relation Presumably: dense environments lead to rapid/early completion of the main star-formation From Peacock et al 2002 More luminous/massive galaxies are more strongly clustered Vatican 2003 Lecture 20 HWR

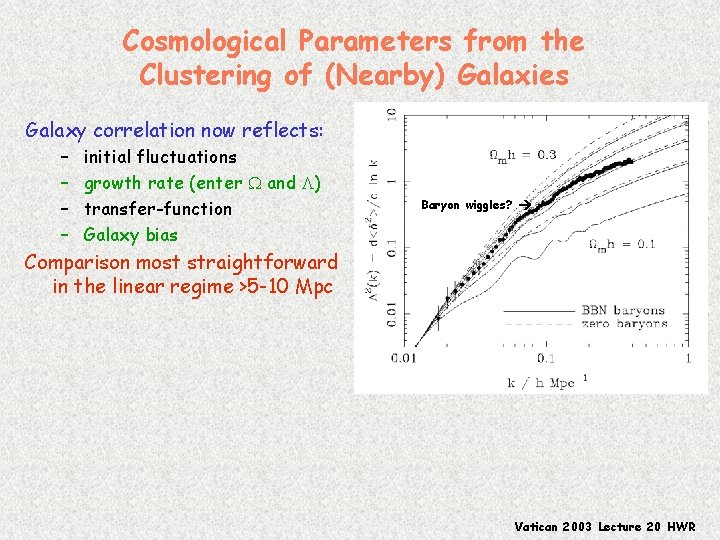
Cosmological Parameters from the Clustering of (Nearby) Galaxies Galaxy correlation now reflects: – – initial fluctuations growth rate (enter and L) transfer-function Galaxy bias Baryon wiggles? Comparison most straightforward in the linear regime >5 -10 Mpc Vatican 2003 Lecture 20 HWR

Mass/Galaxy Clustering at high Redshift • Can one observe the growth of mass fluctuation and galaxy clustering directly? – Put a “point” between the CMB and the present epoch. Two possible probes at z~3: Galaxies (Ly-break galaxies) The fluctuation inter-galactic medium (IGM): Ly-alpha forest Galaxies: from Adelberger, Steidel and collaborators: Ly-break galaxies at z~3 are nearly as clustered as L* galaxies now (massive) galaxies were more biased tracers of the mass fluctuations than they are now. Vatican 2003 Lecture 20 HWR

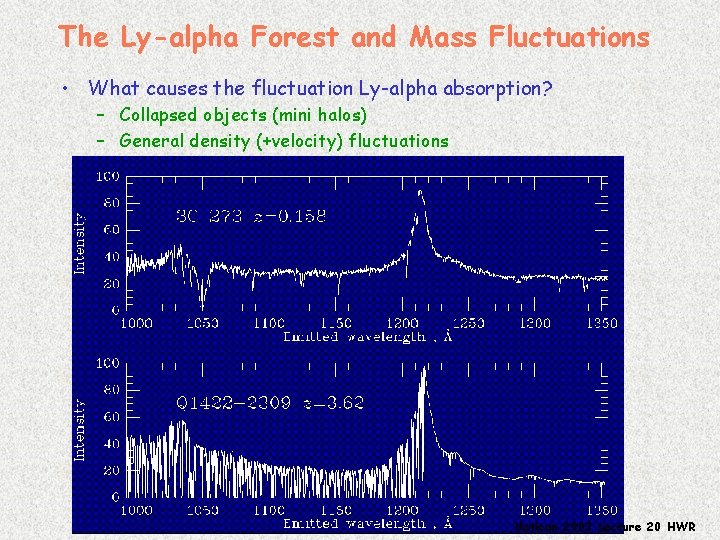
The Ly-alpha Forest and Mass Fluctuations • What causes the fluctuation Ly-alpha absorption? – Collapsed objects (mini halos) – General density (+velocity) fluctuations Vatican 2003 Lecture 20 HWR

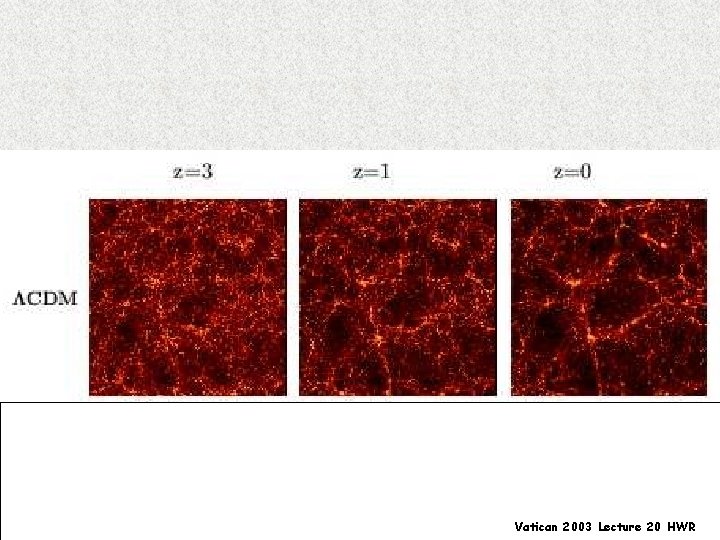
Vatican 2003 Lecture 20 HWR

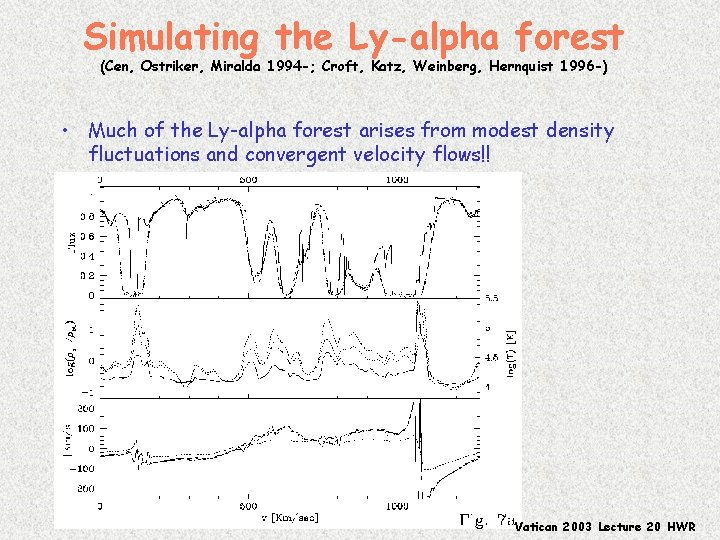
Simulating the Ly-alpha forest (Cen, Ostriker, Miralda 1994 -; Croft, Katz, Weinberg, Hernquist 1996 -) • Much of the Ly-alpha forest arises from modest density fluctuations and convergent velocity flows!! Vatican 2003 Lecture 20 HWR

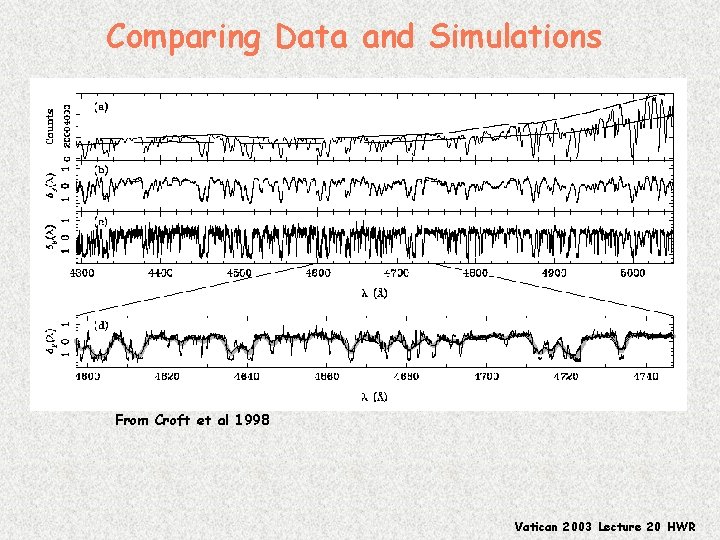
Comparing Data and Simulations From Croft et al 1998 Vatican 2003 Lecture 20 HWR

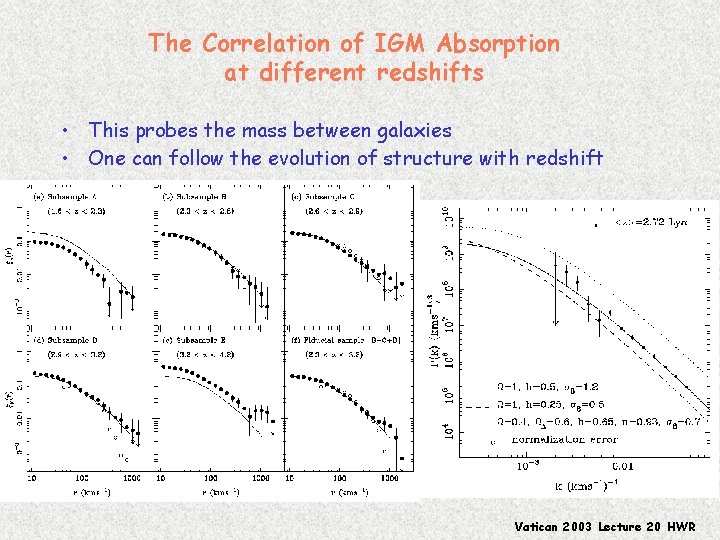
The Correlation of IGM Absorption at different redshifts • This probes the mass between galaxies • One can follow the evolution of structure with redshift Vatican 2003 Lecture 20 HWR

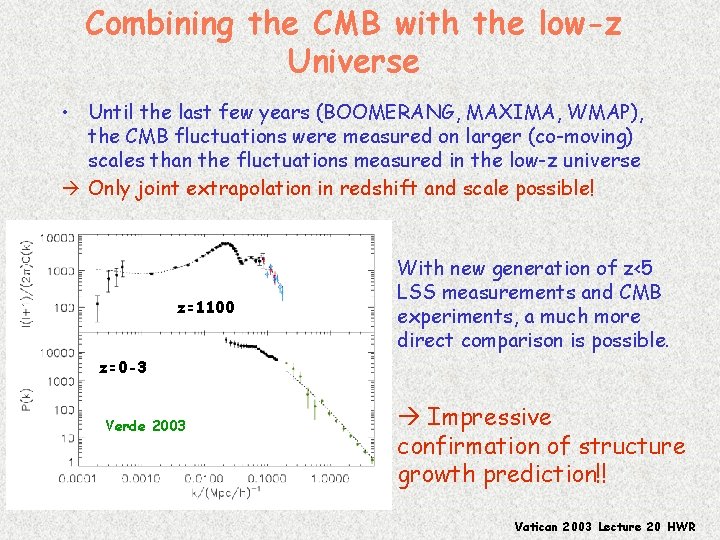
Combining the CMB with the low-z Universe • Until the last few years (BOOMERANG, MAXIMA, WMAP), the CMB fluctuations were measured on larger (co-moving) scales than the fluctuations measured in the low-z universe Only joint extrapolation in redshift and scale possible! z=1100 With new generation of z<5 LSS measurements and CMB experiments, a much more direct comparison is possible. z=0 -3 Verde 2003 Impressive confirmation of structure growth prediction!! Vatican 2003 Lecture 20 HWR

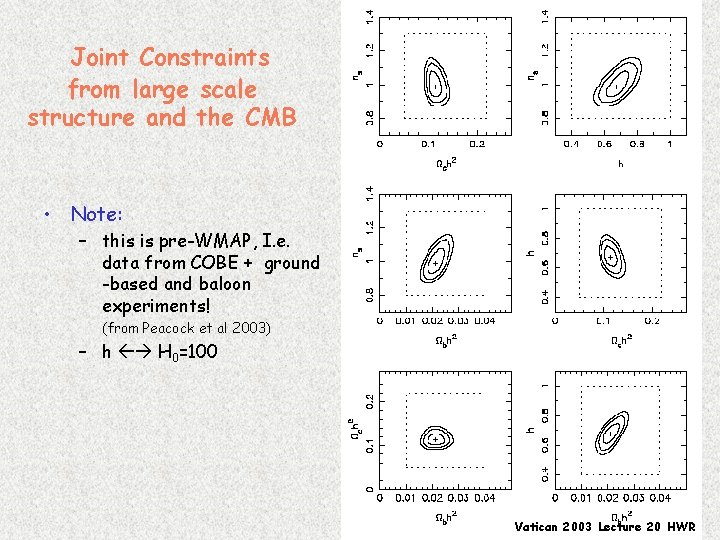
Joint Constraints from large scale structure and the CMB • Note: – this is pre-WMAP, I. e. data from COBE + ground -based and baloon experiments! (from Peacock et al 2003) – h H 0=100 Vatican 2003 Lecture 20 HWR

Vatican 2003 Lecture 20 HWR

Let’s Recapitulate Theory Observations Big Bang Expansion, CMB, BBN Inflation Space is flat, CMB is uniform, fluctuations are scale free FRW/cosmological parameters M=0. 27, L=0. 7, H 0=70 SN Ia, Galaxy Clustering, CMB (Non-baryonic) dark matter dominates Dynamics, lensing, BBN, CMB (small) initial fluctuations CMB Growth of density fluctuations CMB vs large-scale structure IGM fluctuations Galaxy large scale struture Linear Vatican 2003 Lecture 20 HWR

Recapitulation II Theory Observations Non-linear growth of densities N-body, Press-Schechter (dark matter) halo profiles Hierarchical build-up of Structures Abundance, stellar mass and clustering of galaxies dynamics, lensing Observed merging, fewer massive galaxies at high-z(? ) Successive conversion of gas into stars Cooling, Feed-back Enrichment Remaining hot gas in clusters and IGM Vatican 2003 Lecture 20 HWR

Galaxy Properties Observations Recapitulation Theory Global star-formation history and QSO evolution (z>6 to now) Hierarchical merging and gas supply Galaxy luminosity function and colors Gas cooling, feed-back, cold gas supply (as function of z) Morphologies, Bulge/Disk, etc f(z) vs. mass vs. environment Typical Sizes Global Scaling Relations Fundamental plane, Tully-Fisher MBH – s relation Gas Disks Merging Spheroids Hierarchical picture Angular momentum (but is it lost? ) Constant star fraction; similar ang. mom. Good thing to work on… Vatican 2003 Lecture 20 HWR