Observation of Anderson localization of light in nonlinear

Observation of Anderson localization of light in nonlinear nonlocal media Marco Leonetti 1, Salman Karbasi 2, Arash Mafi 2, Claudio Conti 3 • 1: IPCF-CNR c/o Dep. of Physics, Univ. “Sapienza”, Rome, Italy • 2: Dep. of Electr. Eng. and Comp. Sci. , Univ. of Wisconsin-Milwaukee , USA • 3: ISC-CNR and Dep. of Physics, University “Sapienza”, Roma, Italy http: //www. complexlight. org/ http: //www. mlphotonics. it 1 marcoleonetti 1@gmail. com 03/06/2014; Waves and Disorder

www. complexlight. org The Complexlight Lab Optical shocks in complex media S. Gentilini et. al; Opt. Expr 22, 1667 (2014) Random lasers in microstructured materials N. Ghofraniha et. al. ; J. Mater. Chem C. , 1 8128 (2013) Granular active matter V. Folli et. al. Scientific Reports, 3, 2251 (2013) 2 03/06/2014; Waves and Disorder

Observation of Anderson localization of light in nonlinear nonlocal media Marco Leonetti 1, Salman Karbasi 2, Arash Mafi 2, Claudio Conti 3 • 1: IPCF-CNR c/o Dep. of Physics, Univ. “Sapienza”, Rome, Italy • 2: Dep. of Electr. Eng. and Comp. Sci. , Univ. of Wisconsin-Milwaukee , USA • 3: ISC-CNR and Dep. of Physics, University “Sapienza”, Roma, Italy http: //www. complexlight. org/ http: //www. mlphotonics. it 3 marcoleonetti 1@gmail. com 03/06/2014; Waves and Disorder

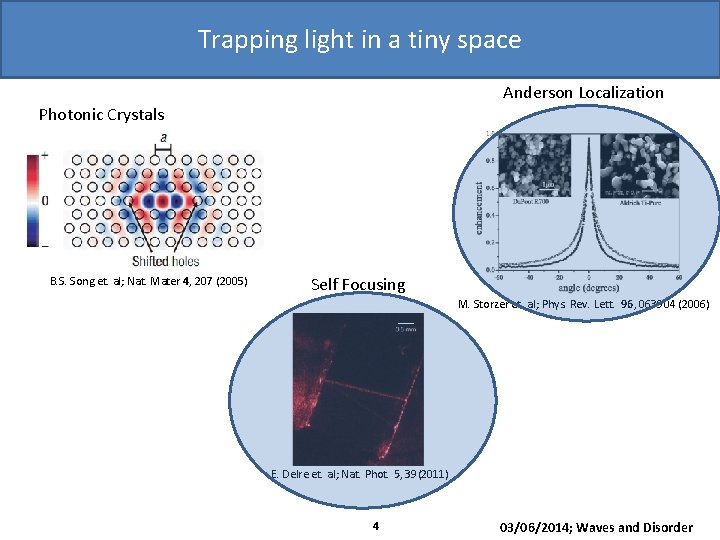
Trapping light in a tiny space Anderson Localization Photonic Crystals B. S. Song et. al; Nat. Mater 4, 207 (2005) Self Focusing M. Storzer et. al; Phys. Rev. Lett. 96, 063904 (2006) E. Delre et. al; Nat. Phot. 5, 39(2011) 4 03/06/2014; Waves and Disorder

Outline • Anderson localization and transversal localization regime • Nonlocality and nonlinearity in the localized regime • Adaptive optics In the localized regime 5 03/06/2014; Waves and Disorder

The Anderson Localization 6 03/06/2014; Waves and Disorder

Transverse Anderson Localization Ioffe- Regel criterion Three dimensional localization Transverse Localization 7 03/06/2014; Waves and Disorder

Transverse localization in optical fibers 2007: Transverse localization with photonic lattices Refractive index mismatch: Δn= 10 -4 8 03/06/2014; Waves and Disorder

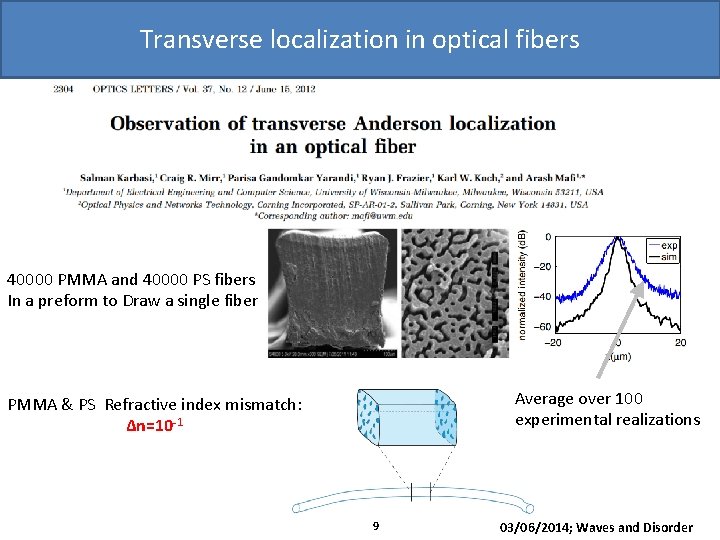
Transverse localization in optical fibers 40000 PMMA and 40000 PS fibers In a preform to Draw a single fiber Average over 100 experimental realizations PMMA & PS Refractive index mismatch: Δn=10 -1 9 03/06/2014; Waves and Disorder

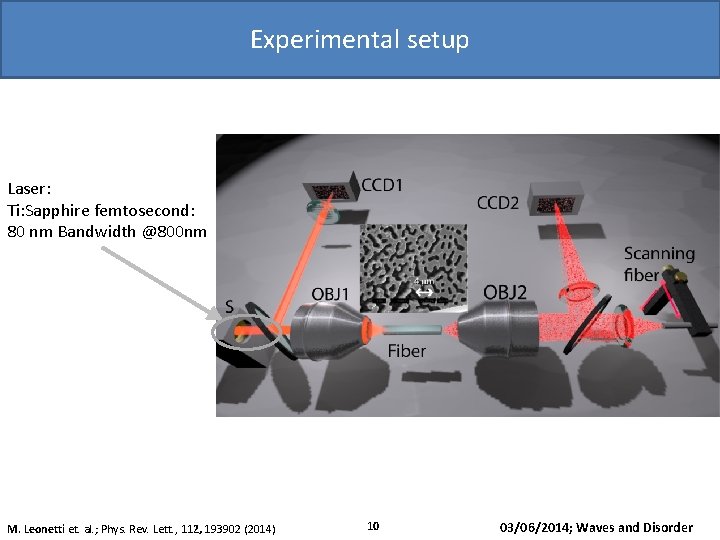
Experimental setup Laser: Ti: Sapphire femtosecond: 80 nm Bandwidth @800 nm M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 10 03/06/2014; Waves and Disorder

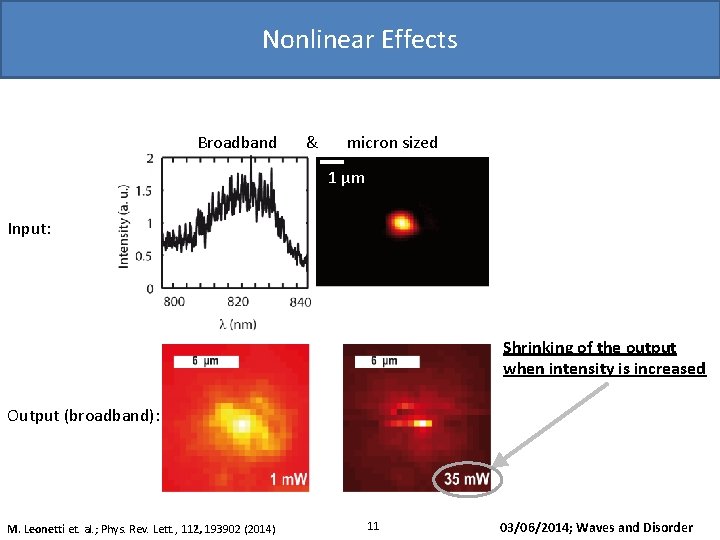
Nonlinear Effects Broadband & micron sized 1 µm Input: Shrinking of the output when intensity is increased Output (broadband): M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 11 03/06/2014; Waves and Disorder

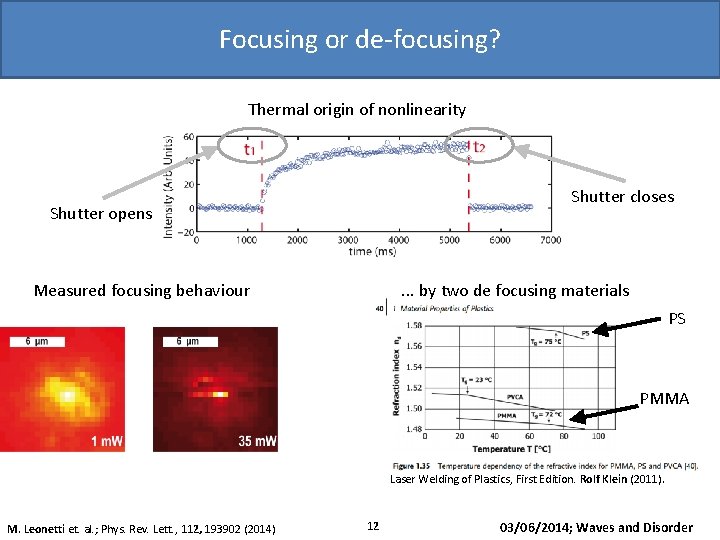
Focusing or de-focusing? Thermal origin of nonlinearity Shutter opens 1 µm Measured focusing behaviour Shutter closes . . . by two de focusing materials PS PMMA Laser Welding of Plastics, First Edition. Rolf Klein (2011). M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 12 03/06/2014; Waves and Disorder

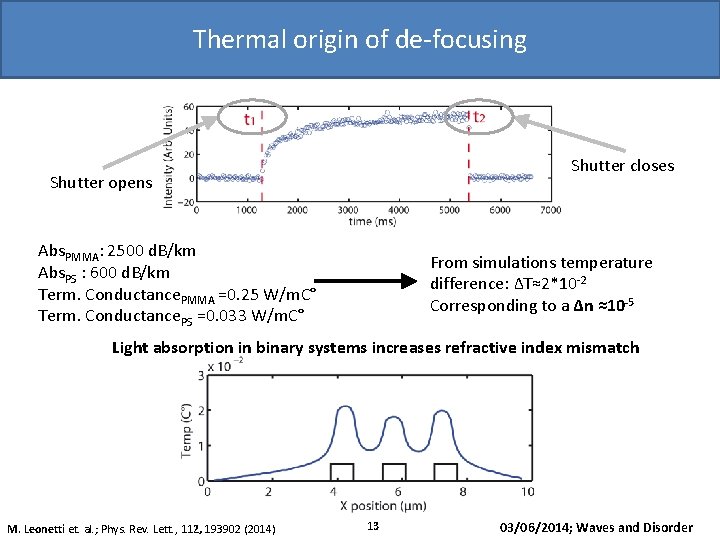
Thermal origin of de-focusing Shutter opens 1 µm Abs. PMMA: 2500 d. B/km Abs. PS : 600 d. B/km Term. Conductance. PMMA =0. 25 W/m. C° Term. Conductance. PS =0. 033 W/m. C° Shutter closes From simulations temperature difference: ΔT≈2*10 -2 Corresponding to a Δn ≈10 -5 Light absorption in binary systems increases refractive index mismatch M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 13 03/06/2014; Waves and Disorder

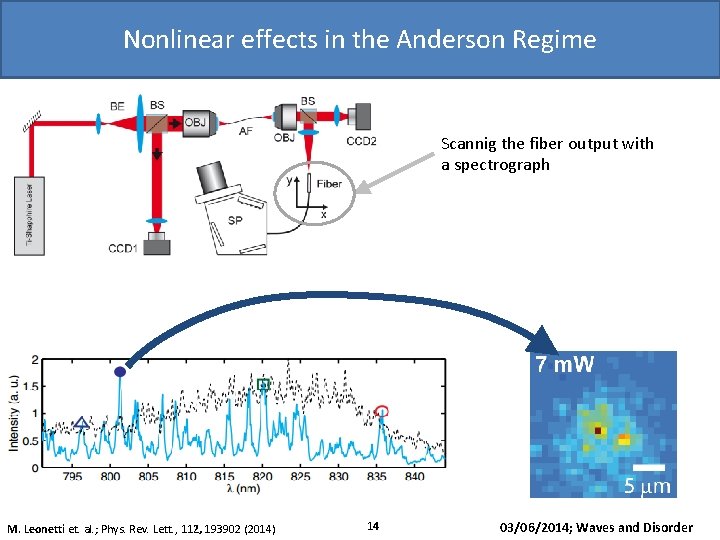
Nonlinear effects in the Anderson Regime 1 µm M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 14 Scannig the fiber output with a spectrograph 03/06/2014; Waves and Disorder

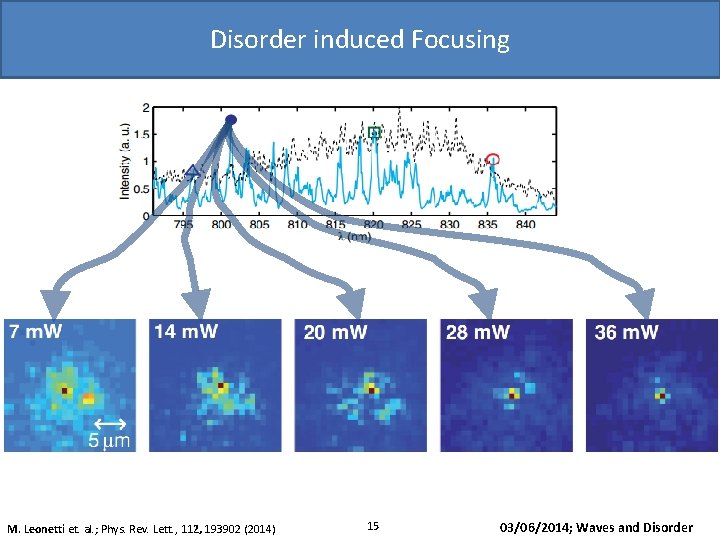
Disorder induced Focusing 1 µm M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 15 03/06/2014; Waves and Disorder

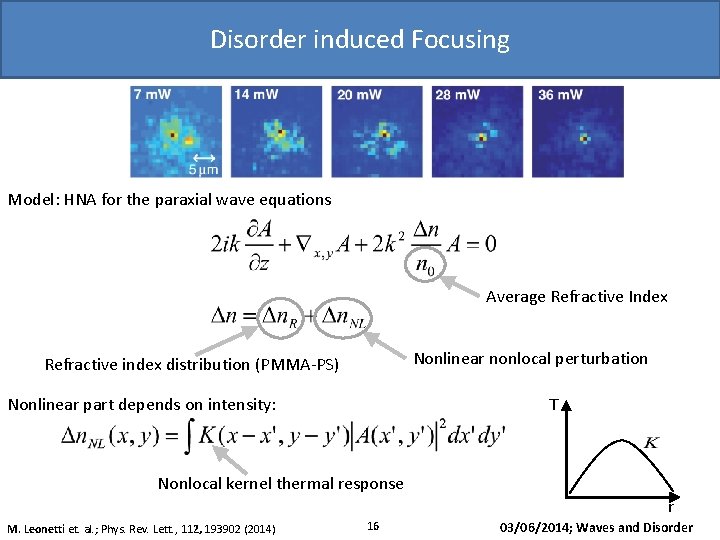
Disorder induced Focusing Model: HNA for the paraxial wave equations 1 µm Average Refractive Index Nonlinear nonlocal perturbation Refractive index distribution (PMMA-PS) Nonlinear part depends on intensity: T Nonlocal kernel thermal response r M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 16 03/06/2014; Waves and Disorder

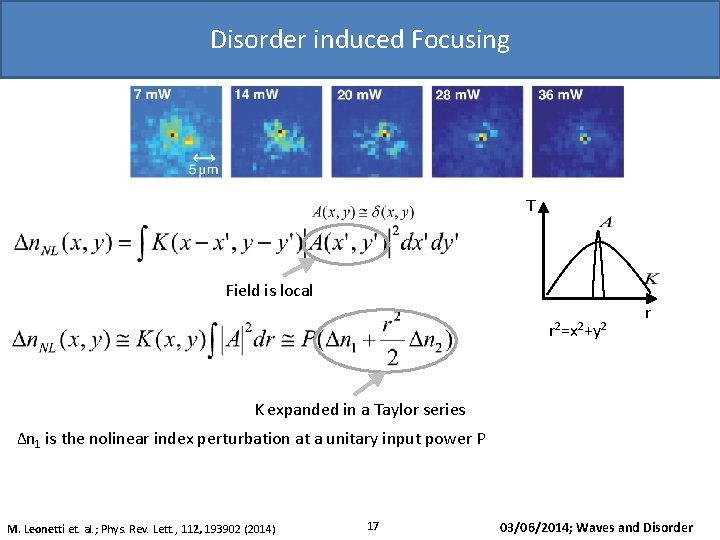
Disorder induced Focusing 1 µm T Field is local r 2=x 2+y 2 r K expanded in a Taylor series Δn 1 is the nolinear index perturbation at a unitary input power P M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 17 03/06/2014; Waves and Disorder

Disorder induced Focusing 1 µm Searching solutions like wave equation becomes: The main effect of nonlinearity is modify the refractive index: that is to shift eigenvalues of the disorder induced localized states Eigenvalues are: M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) Localization length: 18 03/06/2014; Waves and Disorder

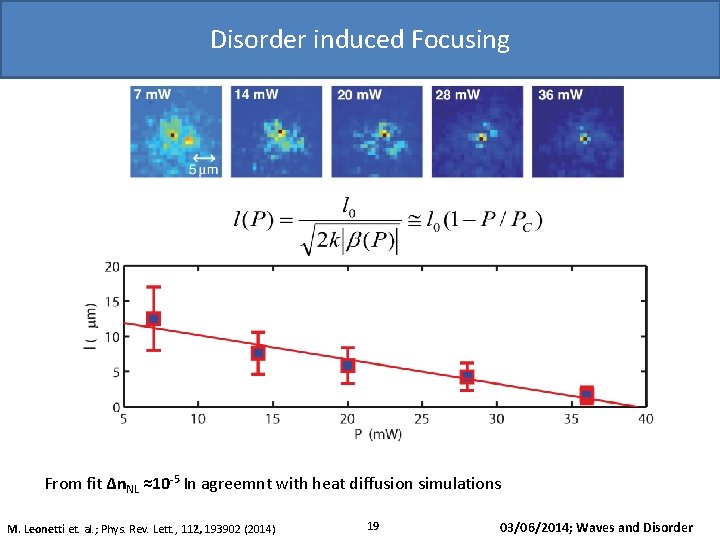
Disorder induced Focusing 1 µm From fit Δn. NL ≈10 -5 In agreemnt with heat diffusion simulations M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 19 03/06/2014; Waves and Disorder

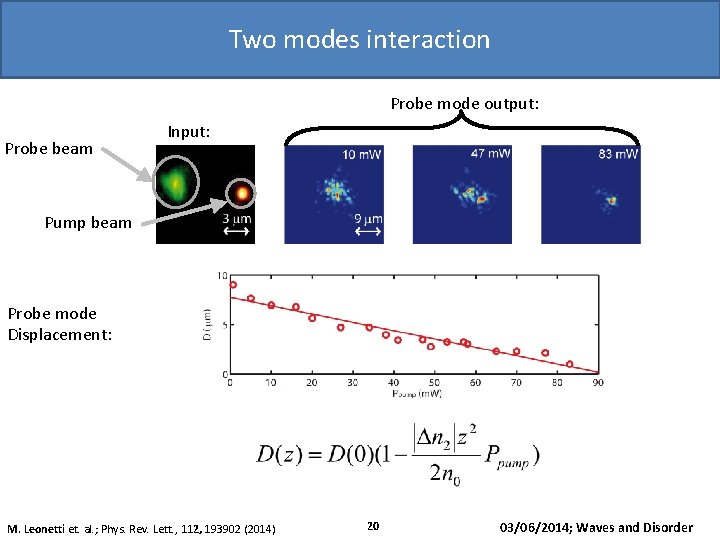
Two modes interaction Probe mode output: Probe beam Input: Pump beam Probe mode Displacement: M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 20 03/06/2014; Waves and Disorder

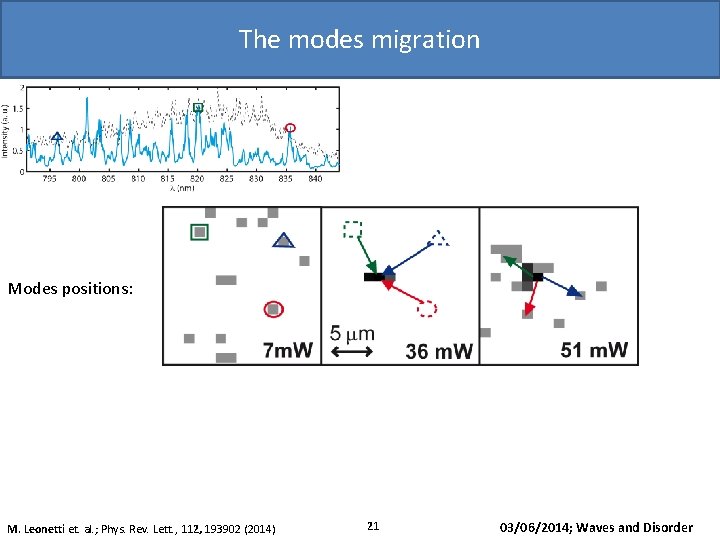
The modes migration Modes positions: M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 21 03/06/2014; Waves and Disorder

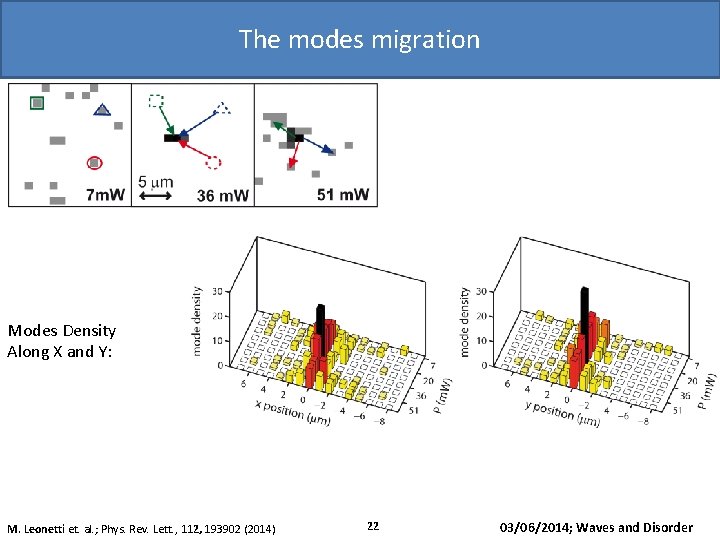
The modes migration Modes Density Along X and Y: M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) 22 03/06/2014; Waves and Disorder

Part I : Conclusions • Transversal Localization in Optical fibers • Disorder induced self-focusing • Nolocality induced modes migration • Controlled beam steering in systems with transverse disorder M. Leonetti et. al. ; Submitted 23 03/06/2014; Waves and Disorder

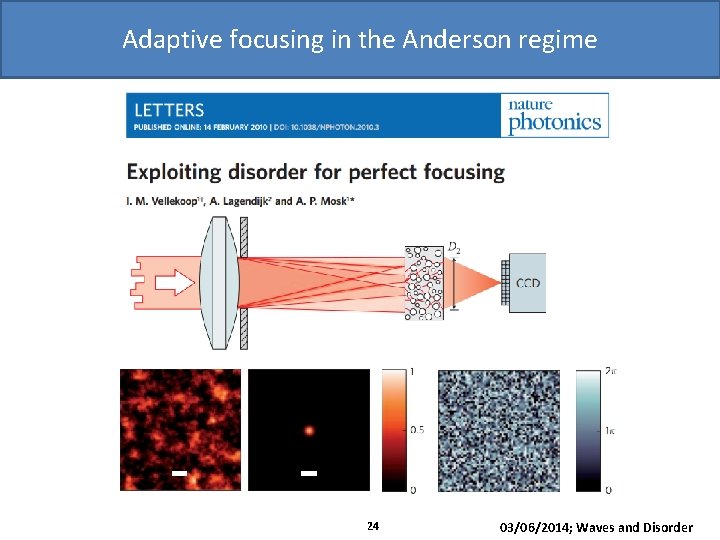
Adaptive focusing in the Anderson regime 24 03/06/2014; Waves and Disorder

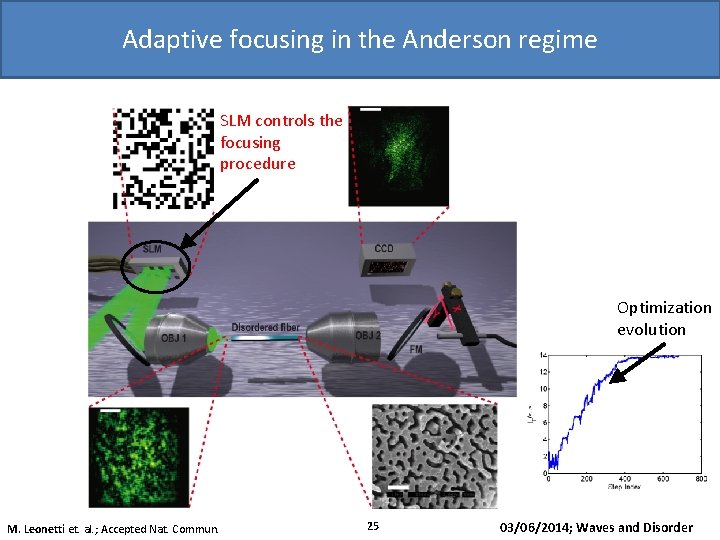
Adaptive focusing in the Anderson regime SLM controls the focusing procedure Optimization evolution M. Leonetti et. al. ; Accepted Nat. Commun. 25 03/06/2014; Waves and Disorder

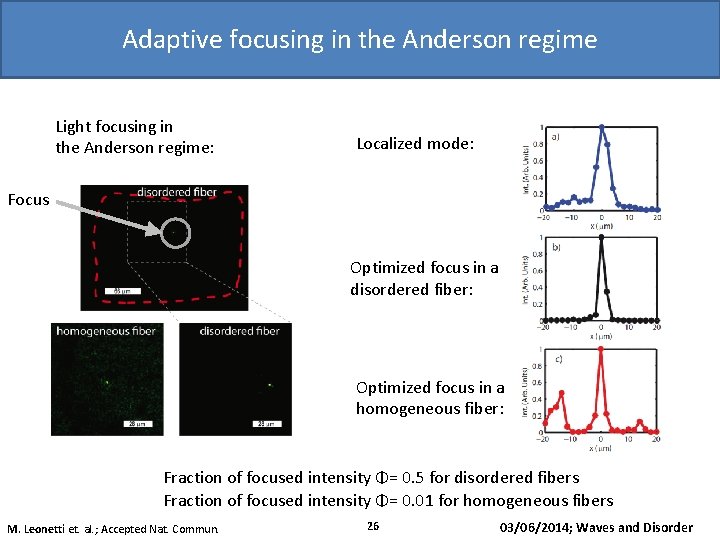
Adaptive focusing in the Anderson regime Light focusing in the Anderson regime: Localized mode: Focus Optimized focus in a disordered fiber: Optimized focus in a homogeneous fiber: Fraction of focused intensity Φ= 0. 5 for disordered fibers Fraction of focused intensity Φ= 0. 01 for homogeneous fibers M. Leonetti et. al. ; Accepted Nat. Commun. 26 03/06/2014; Waves and Disorder

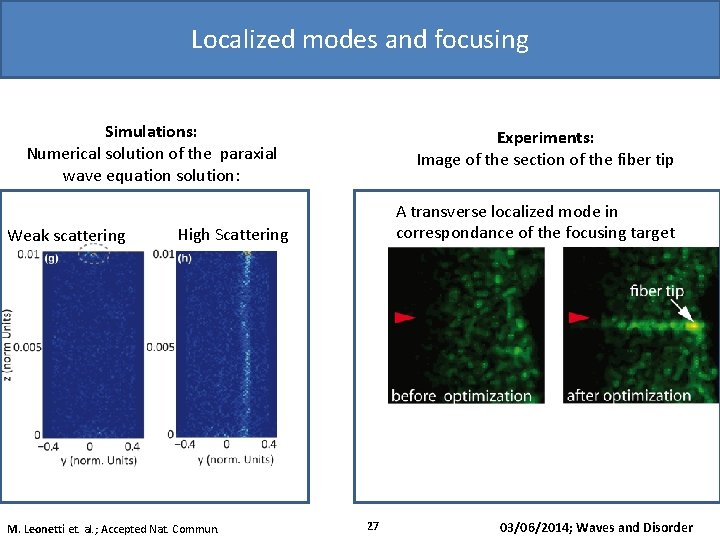
Localized modes and focusing Simulations: Numerical solution of the paraxial wave equation solution: Weak scattering Experiments: Image of the section of the fiber tip A transverse localized mode in correspondance of the focusing target High Scattering M. Leonetti et. al. ; Accepted Nat. Commun. 27 03/06/2014; Waves and Disorder

Conclusions Part I: • Disorder induced focusing and migration in the transversal localization regime Part II: • Adaptive focusing in the Transversal localization regime • Coexistence between localized modes and adaptive focusing • Increased fraction of light gathered to target 28 03/06/2014; Waves and Disorder

Thank you for the attention • Observation of Migrating Transverse Anderson Localizations of Light in Nonlocal Media M. Leonetti et. al. ; Phys. Rev. Lett. , 112, 193902 (2014) • Light Focusing in the Anderson Regime M. Leonetti et. Al; Accepted Nat. Commun. http: //www. complexlight. org/ http: //www. mlphotonics. it 29 marcoleonetti 1@gmail. com 03/06/2014; Waves and Disorder