Objetivo Resolver problemas que involucran las reglas de

Objetivo: Resolver problemas que involucran las reglas de las probabilidades, de manera concreta, pictórica y simbólica. Segundo Medio B, C, D y E

Instrucciones: Vea la presentación en pantalla completa. Lea cuidadosamente cada definición y ejemplo, tome los apuntes correspondientes y desarrolle los ejercicios y problemas propuestos. En caso de dudas y/o consultas, puede comunicarse al correo estefani. torres@luisalbertobarrera. cl, dando a conocer su inquietud.

Probabilidad Clásica P(A) = Casos favorables Casos posibles Ésta es la fórmula que ocuparemos para calcular probabilidades (que dice: la probabilidad del evento A es igual a los casos favorables del experimento, dividido los casos posibles del experimento)

Ejemplo: Consideremos el experimento lanzar un dado ¿Cuál es la probabilidad de que al lanzar un dado común salga un número par? Identificamos el evento A. A: que salga número par (es lo que me están preguntando) Para aplicar la fórmula debemos contar los casos posibles de lanzar un dado y los casos favorables (de que salga un número par, porque eso me están preguntando) El dado común tiene seis caras y al lanzarlo me puede salir un 1, un 2, un 3 , un 4, un 5 o un 6. Contamos estos casos (que salga el 1, el 2, el 3, el 4, el 5 y el 6) y son seis casos en total. (aquí sabemos que los casos totales son 6) Que salga un número par (que es el evento A) debemos considerar cuales son los números pares que podrían salir si lanzamos el dado, en este caso será: el 2, el 4 y el 6, los contamos y serían 3 casos favorables (donde me puede aparecer par) Entonces Aplicamos la : fórmula: Casos favorables : Simplificamos por 3 3 Casos posibles: 6

¿Cuál es la probabilidad de que al lanzar un dado salga un número mayor que dos? Evento A: que salga un número mayor que dos Casos favorables : (que salga el 3, el 4, el 5 y el 6, los contamos y son 4) 4 Casos posibles: 6 (que salga el 1, el 2, el 3, el 4, el 5 y el 6. Los contamos y son 6) Aplicamos la fórmula: ¿Cuál es la probabilidad de que al lanzar un dado salga un número primo? Evento A: que salga un número primo. Casos favorables : 3 Casos posibles: 6 Aplicamos la fórmula: Los Números primos son: 2, 3, 5, 7, 11, 13, 17, etc (que salga el 2, el 3 y el 5. Estos son los números primos, los contamos y son 3) (que salga el 1, el 2, el 3, el 4, el 5 y el 6. Los contamos y son 6)

En la siguiente urna hay 8 bolitas numeradas del 1 al 8. ¿Cuál es la probabilidad de que sacar una bolita salga un número menor que 3? Evento A: que salga un número menor que 3. Si sacamos una bolita al azar me podría salir una bolita con el número 1, con el 2, con el 3, con el 4, con el 5, con el 6, con el 7 y con el 8. Los contamos y serían 8 casos posibles en total. En el caso de que salga un número menor que 3, podría salir una bolita con el número 1 y con el número 2, de ahí ya no se podrían contar los otros porque no serían números menores que 3. Contamos los casos y serían 2 casos favorables en total (el número 1 y 2 solamente). Casos favorables : 2 Aplicamos la fórmula: Casos posibles: 8

¿Cuál es la probabilidad de que sacar una bolita salga un número mayor o igual a 4? Evento A: que salga un número mayor o igual a 4. Si sacamos una bolita al azar me podría salir una bolita con el número 1, con el 2, con el 3, con el 4, con el 5, con el 6, con el 7 y con el 8. Los contamos y serían 8 casos posibles en total. En el caso de que salga el evento, un número mayor o igual a 4, podría salir una bolita con el número 4, el 5, el 6, el 7 y el 8. Los contamos y serían 5 casos favorables en total. Casos favorables : 5 Aplicamos la fórmula: Casos posibles: 8
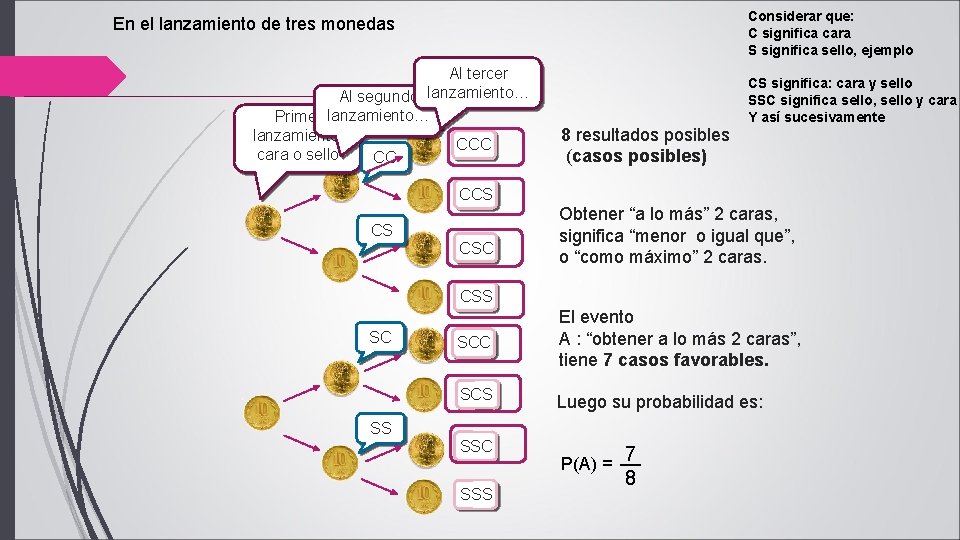
Considerar que: C significa cara S significa sello, ejemplo En el lanzamiento de tres monedas Al tercer Al segundo lanzamiento… Primer lanzamiento… lanzamiento, CCC cara o sello CC 8 resultados posibles (casos posibles) CS significa: cara y sello SSC significa sello, sello y cara Y así sucesivamente CCS CS CSC Obtener “a lo más” 2 caras, significa “menor o igual que”, o “como máximo” 2 caras. CSS SC SCC El evento A : “obtener a lo más 2 caras”, tiene 7 casos favorables. SCS Luego su probabilidad es: SSC P(A) = 7 SS SSS 8

Ahora conoceremos otras dos fórmulas del cálculo de probabilidades que se utilizan cuando en un experimento me piden calcular la probabilidad de dos eventos distintos.

Cada vez que me pidan calcular la probabilidad de que ocurran dos eventos, por ejemplo: ü Que salga un número par o un número mayor que 5. ü Que salga un bolita de color amarillo o una bolita de color verde. ü Que en una baraja de naipes ingleses salga un corazón o un número 2. Identificaremos los dos eventos, a uno lo llamaremos evento A y al otro evento B. ü Que salga un número par o un número mayor que 5. Evento A Evento B ü Que salga un bolita de color amarillo o una bolita de color verde. Evento A Evento B ü Que en una baraja de naipes ingleses salga un corazón o un número 2. Evento A Evento B

Analicemos los eventos de la siguiente forma: ü Que salga un número par o un número mayor que 5. Supongamos: Número par = 2, 4, 6, 8, 10, 12, etc Número mayor que 5 = 6, 7, 8, 9, 10, etc. Nos preguntamos: ¿hay elementos en común entre los dos eventos? . La respuesta es si, puesto que se repiten el número 6, 8, 10, etc. ü Que salga un bolita de color amarillo o una bolita de color verde. Supongamos: Bolita amarilla: pueden salir dependiendo de la cantidad que hayan puesto. Bolita verde: pueden salir dependiendo de la cantidad que hayan puesto. Nos preguntamos: ¿hay elementos en común entre los dos eventos? . La respuesta es no, las bolitas amarillas, son sólo de color amarilla y las bolitas verdes son sólo de color verde. Siempre debemos analizar la situación y ver si hay elementos comunes entre ellos, lo cual nos permitirá decidir que fórmula utilizaremos:
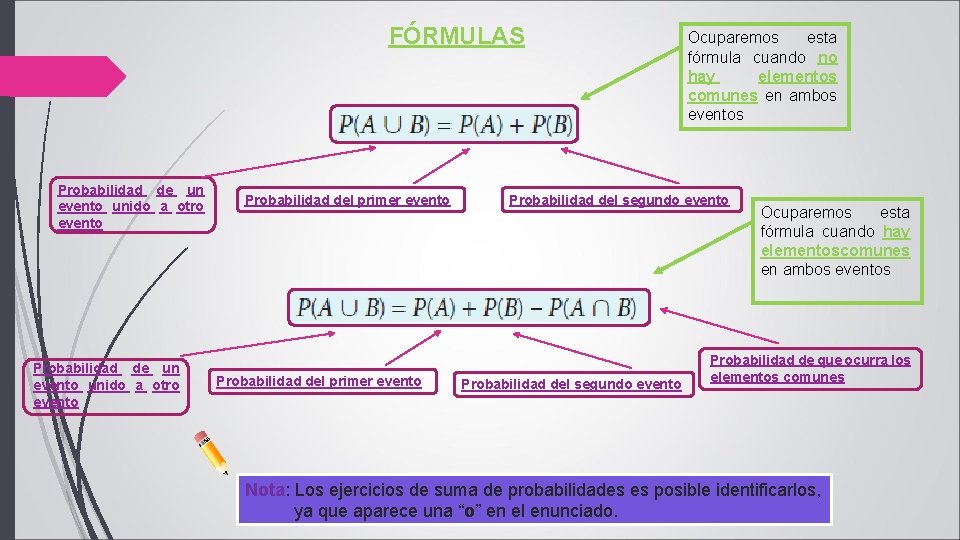
FÓRMULAS Probabilidad de un evento unido a otro evento Probabilidad del primer evento Ocuparemos esta fórmula cuando no hay elementos comunes en ambos eventos Probabilidad del segundo evento Ocuparemos esta fórmula cuando hay elementoscomunes en ambos eventos Probabilidad de que ocurra los elementos comunes Nota: Los ejercicios de suma de probabilidades es posible identificarlos, ya que aparece una “o” en el enunciado.
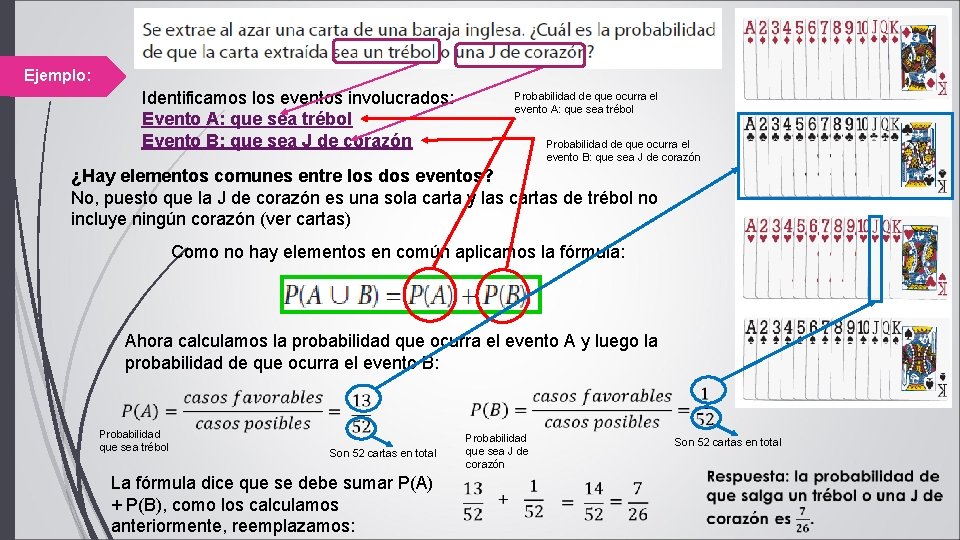
Ejemplo: Identificamos los eventos involucrados: Evento A: que sea trébol Evento B: que sea J de corazón Probabilidad de que ocurra el evento A: que sea trébol Probabilidad de que ocurra el evento B: que sea J de corazón ¿Hay elementos comunes entre los dos eventos? No, puesto que la J de corazón es una sola carta y las cartas de trébol no incluye ningún corazón (ver cartas) Como no hay elementos en común aplicamos la fórmula: Ahora calculamos la probabilidad que ocurra el evento A y luego la probabilidad de que ocurra el evento B: Probabilidad que sea trébol Son 52 cartas en total La fórmula dice que se debe sumar P(A) + P(B), como los calculamos anteriormente, reemplazamos: Probabilidad que sea J de corazón Son 52 cartas en total

Ejemplo: Identificamos los eventos involucrados: Evento A: que sea trébol Evento B: que sea J Probabilidad de que ocurra el evento A: que sea trébol Probabilidad de que ocurra el evento B: que sea J ¿Hay elementos comunes entre los dos eventos? SI, que sea trébol puede ser A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q y K. y que se J puede ser de corazón, diamante, trébol o de pica. En los dos eventos se repite la J de trébol Probabilidad de que ocurra el evento repetido. Como hay elementos en común aplicamos la fórmula:
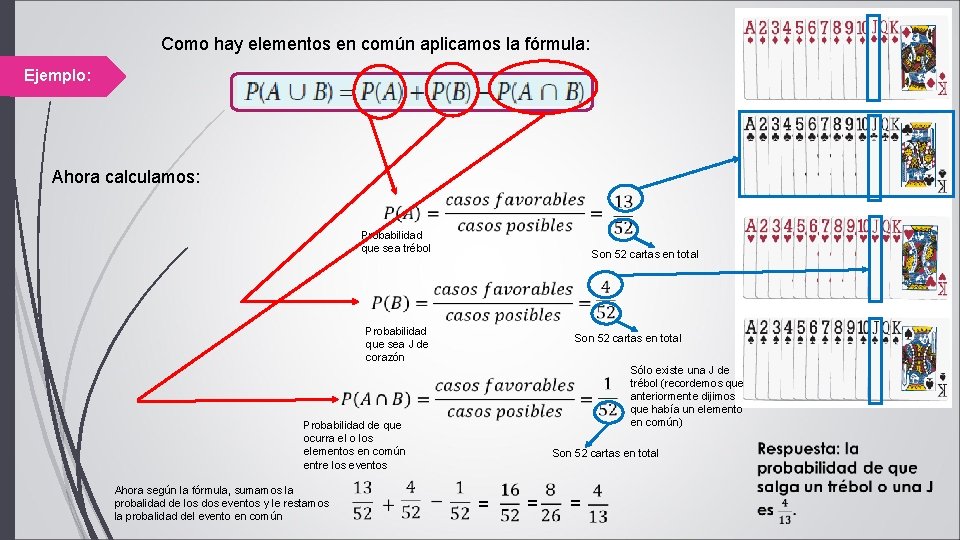
Como hay elementos en común aplicamos la fórmula: Ejemplo: Ahora calculamos: Probabilidad que sea trébol Son 52 cartas en total Probabilidad que sea J de corazón Son 52 cartas en total Sólo existe una J de trébol (recordemos que anteriormente dijimos que había un elemento en común) Probabilidad de que ocurra el o los elementos en común entre los eventos Ahora según la fórmula, sumamos la probalidad de los dos eventos y le restamos la probalidad del evento en común Son 52 cartas en total = = =
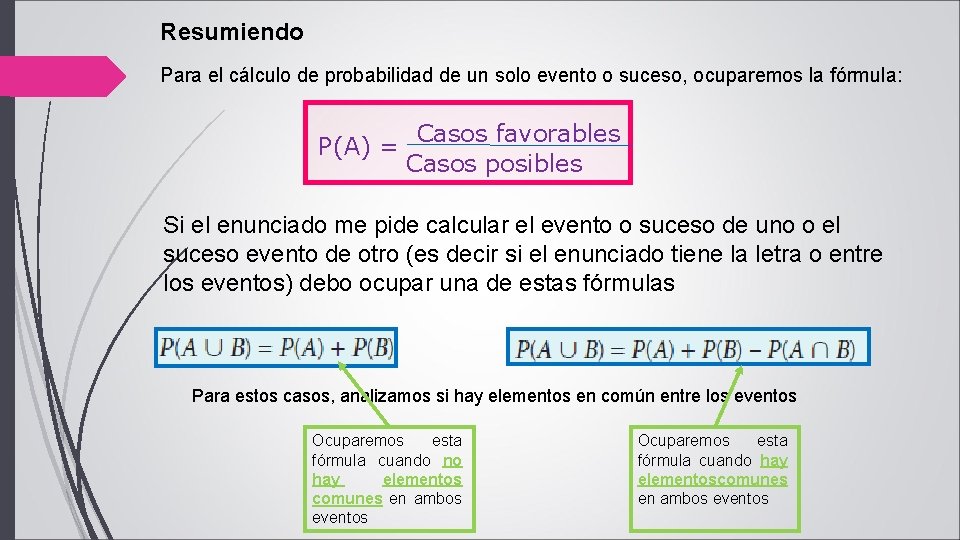
Resumiendo Para el cálculo de probabilidad de un solo evento o suceso, ocuparemos la fórmula: P(A) = Casos favorables Casos posibles Si el enunciado me pide calcular el evento o suceso de uno o el suceso evento de otro (es decir si el enunciado tiene la letra o entre los eventos) debo ocupar una de estas fórmulas Para estos casos, analizamos si hay elementos en común entre los eventos Ocuparemos esta fórmula cuando no hay elementos comunes en ambos eventos Ocuparemos esta fórmula cuando hay elementoscomunes en ambos eventos
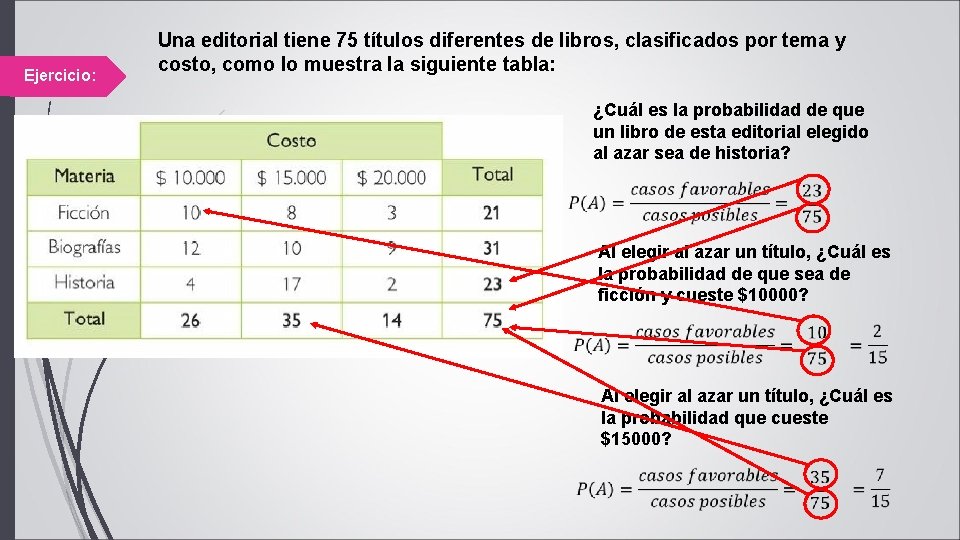
Ejercicio: Una editorial tiene 75 títulos diferentes de libros, clasificados por tema y costo, como lo muestra la siguiente tabla: ¿Cuál es la probabilidad de que un libro de esta editorial elegido al azar sea de historia? Al elegir al azar un título, ¿Cuál es la probabilidad de que sea de ficción y cueste $10000? Al elegir al azar un título, ¿Cuál es la probabilidad que cueste $15000?

¡Buen trabajo! Ejercita con las actividades de la guía de trabajo correspondiente, RECUERDA QUE ANTE CUALQUIER DUDA QUE TENGAS PUEDES CONTACTARTE CON TU PROFESORA, estefani. torres@luisalbertobarrera. cl
- Slides: 18